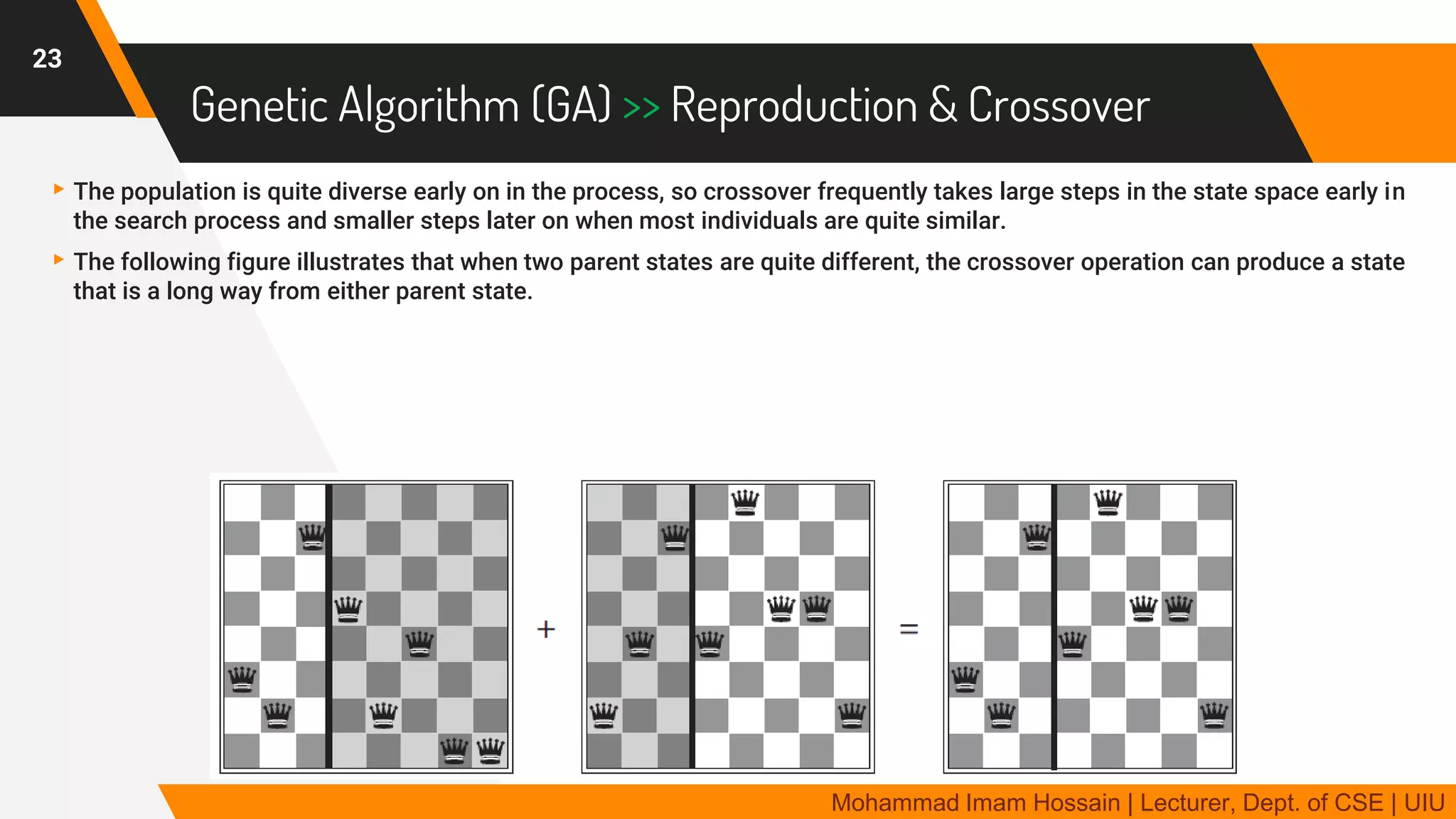
The document discusses local search algorithms as an alternative to classical search algorithms when the path to the goal state is irrelevant. It describes hill-climbing search, which iteratively moves to a neighboring state with improved value. Hill-climbing can get stuck at local optima. Variations like simulated annealing and stochastic hill-climbing incorporate randomness to avoid local optima. Genetic algorithms use techniques inspired by evolution like selection, crossover and mutation to search the state space. The document uses examples like the 8-queens and 8-puzzle problems to illustrate local search concepts.












![Hill-climbing Search >> Variations
▸Stochastic hill-climbing
- Random selection among the uphill/downhill moves.
- The selection probability can vary with the steepness of the uphill move.
Sample Algorithm [Uphill version] >>
13
Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU
eval(vc) = 107, T = const = 10](https://image.slidesharecdn.com/localsearch-200606074207/75/AI-5-Local-Search-13-2048.jpg)