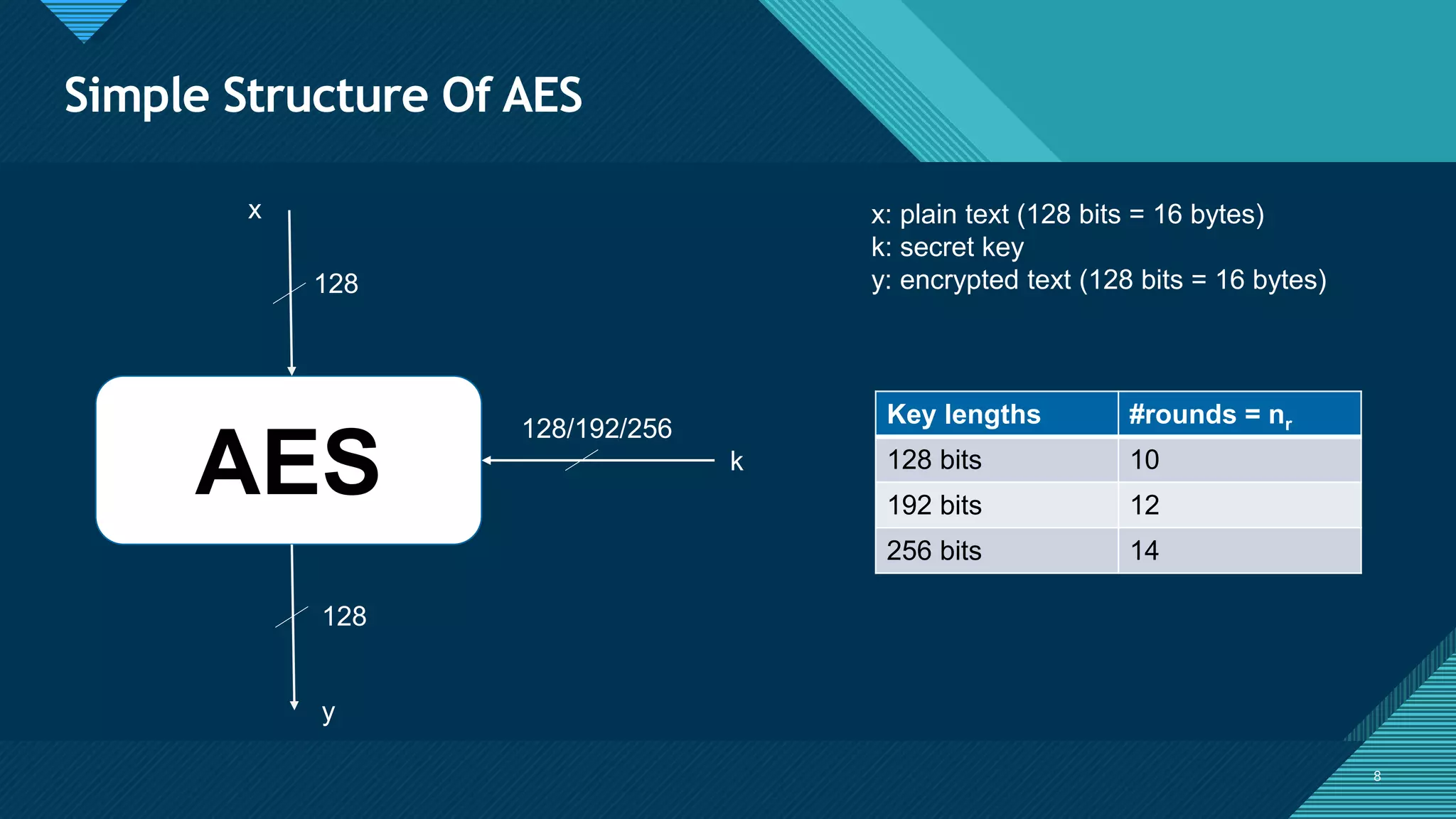
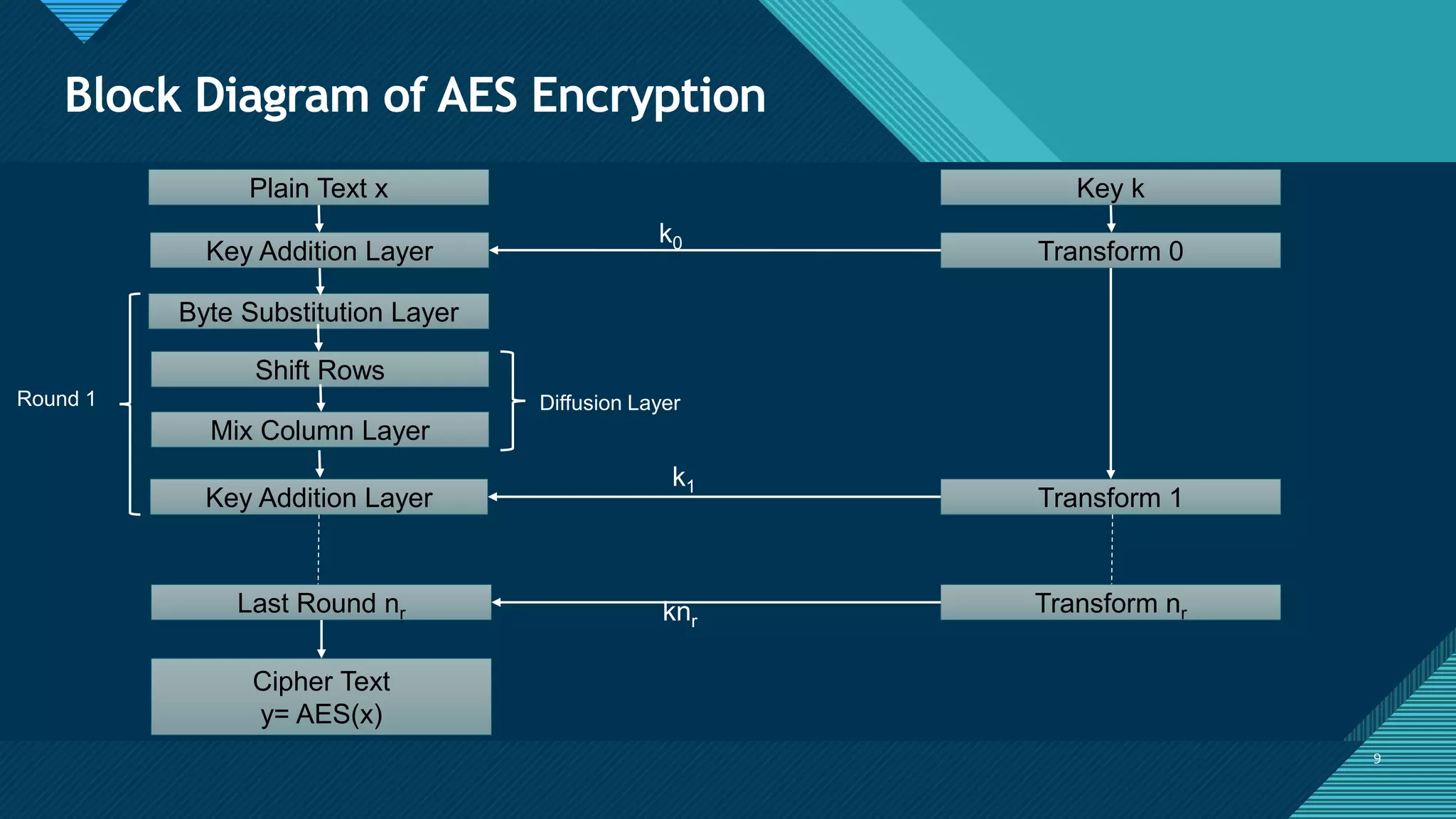
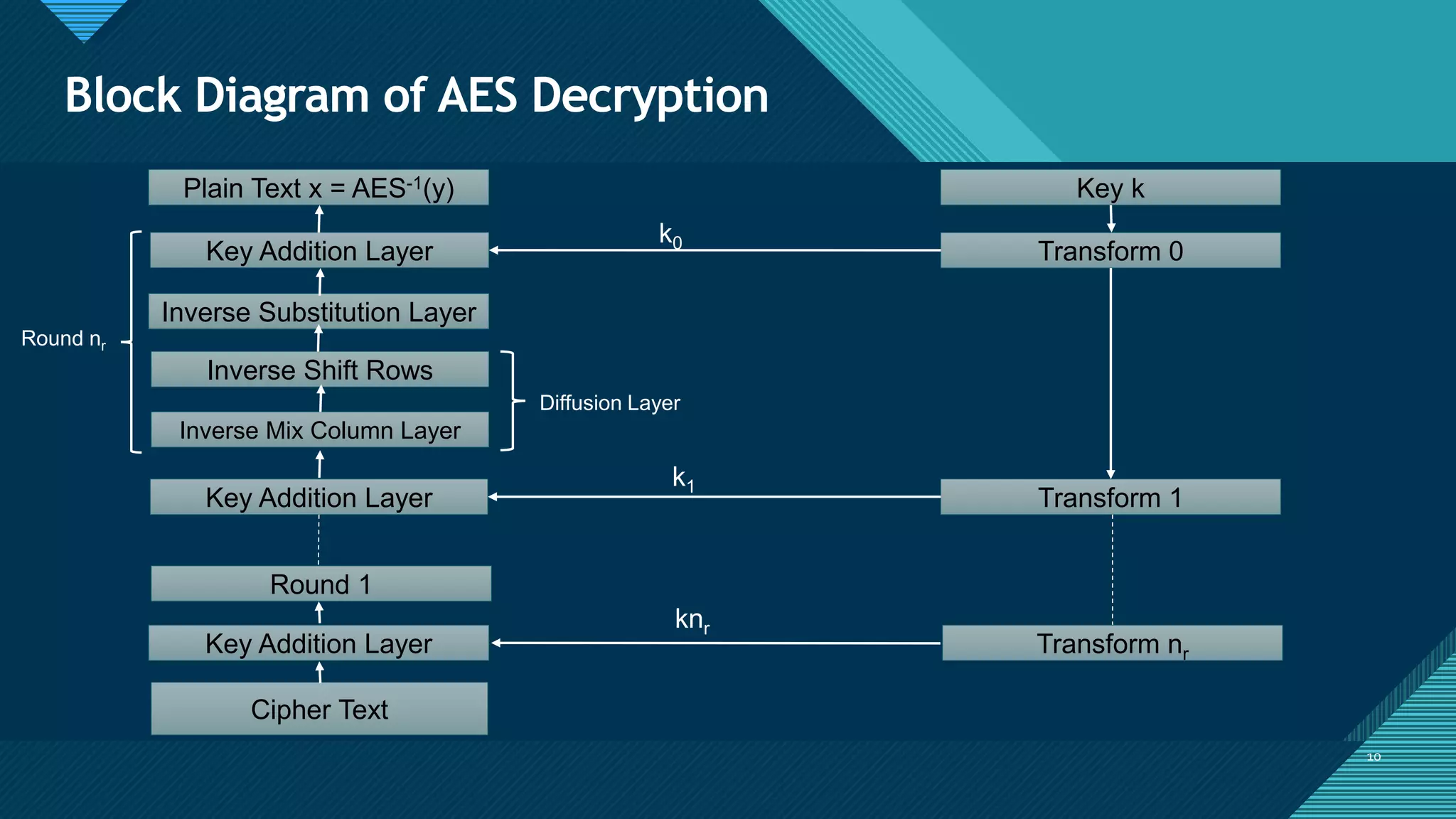
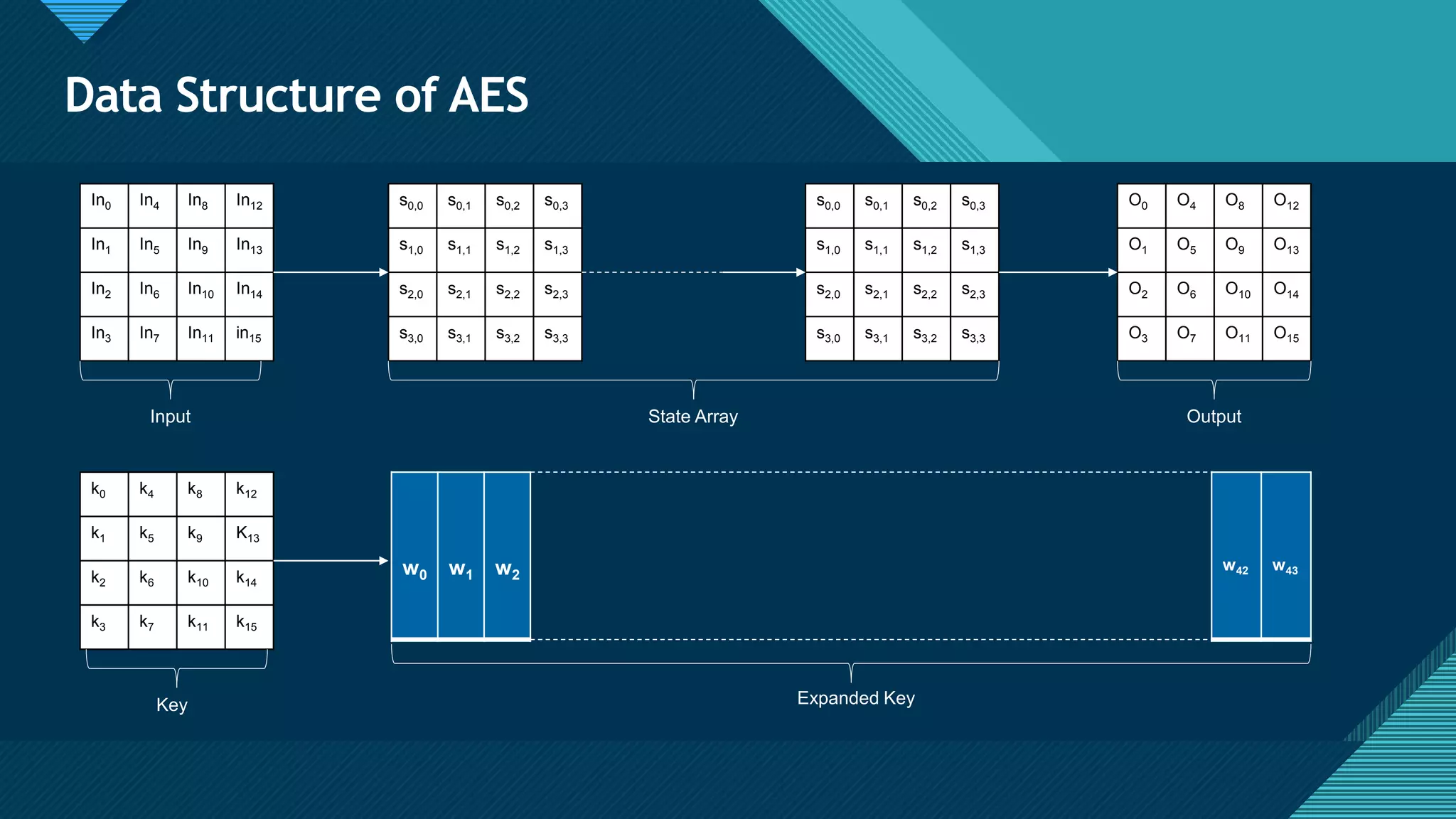
The document provides an overview of the Advanced Encryption Standard (AES), a symmetric block cipher adopted by the US government for protecting classified information and widely used for encrypting sensitive data globally. It compares AES with the previous Data Encryption Standard (DES), emphasizing AES's greater security and structure, which includes processes like key expansion and various transformation functions. Additionally, real-world applications of AES, particularly in end-to-end encryption for chat systems like WhatsApp, underline its importance in modern cybersecurity.



















![Click to edit Master title style
27
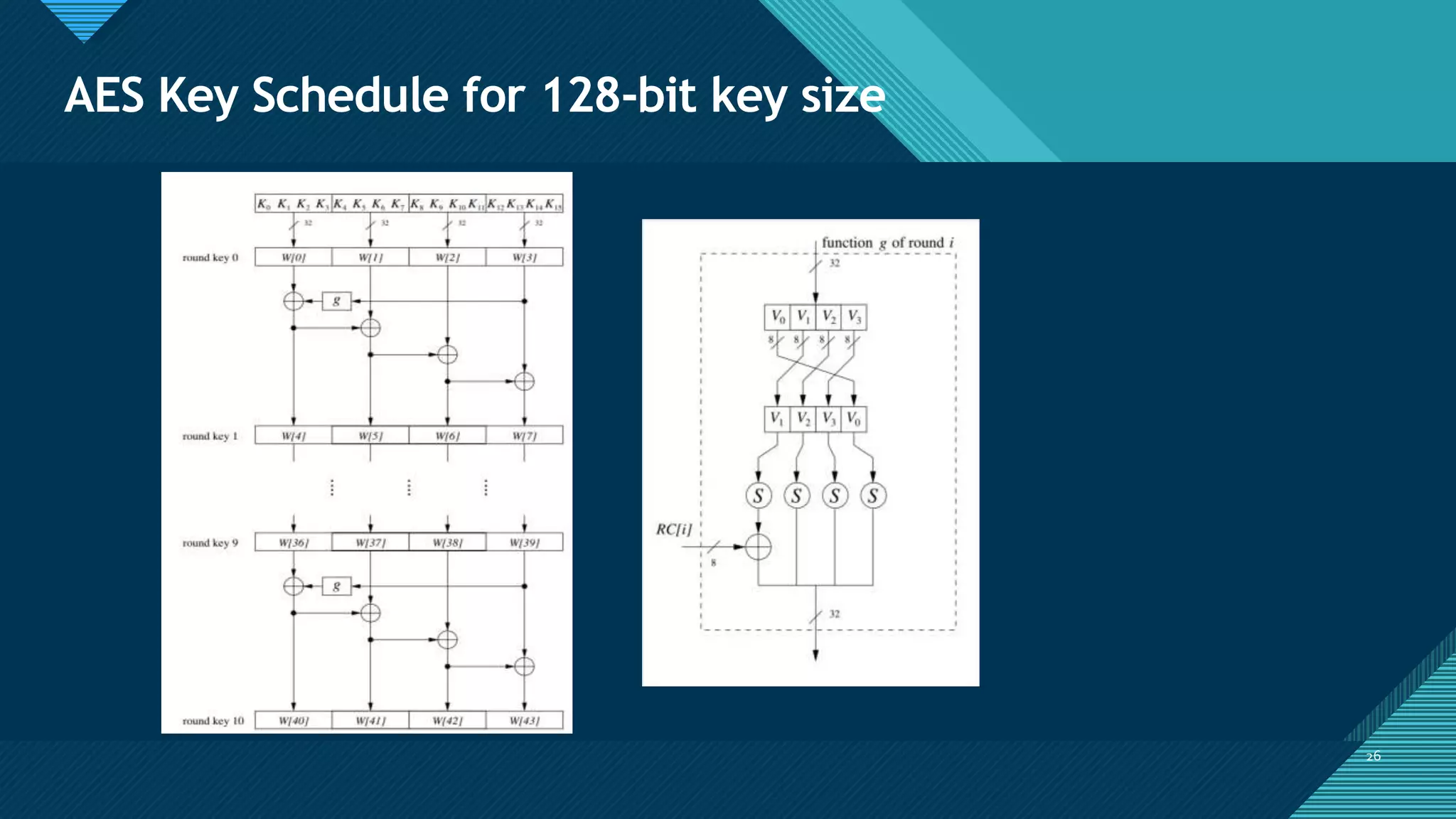
Key Expansion Algorithm
27
keyExpansion(byte key[16], word[44]) {
word temp;
for(i = 0 ; i < 4 ; i++) {
w[i] = (key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]);
}
for(i = 4 ; i < 44 ; i++) {
temp = w[i - 1];
if (i mod 4 == 0)
temp = subWord(rotWord(temp)) Rcon[i/4];
w[i] = w[i - 4] temp;
}
}](https://image.slidesharecdn.com/advancedencryptionstandardugreseacrh-200926183433/75/Advanced-encryption-standard-ug-reseacrh-27-2048.jpg)


