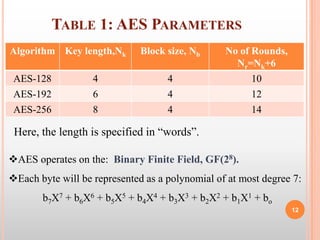
The document describes a modified AES key expansion algorithm for image encryption and decryption. It discusses basics of cryptography and image encryption. It introduces AES and describes the standard AES key expansion process. It then presents a modified AES key expansion algorithm tailored for images where the keys are expanded based on image pixel count, Rcon values are derived from the initial key, and the S-box is shifted based on the initial key. It analyzes the proposed algorithm and shows it offers high encryption quality with minimal time compared to previous techniques.

1. IMAGE ENCRYPTION/DECRYPTION
USING MODIFIED AES KEY
EXPANSION
1
presented by
SREEDA P (4PA09TE034)
8th Semester TE, PACE.

2. CONTENTS
 Basics of Cryptography.
 Introduction to Image Encryption.
 Previous Works.
 Introduction to AES.
 Modified AES Key Expansion Algorithm.
 Simulation Results.
 Comparison with previous techniques.
 Conclusion & Future scope.
2
 References.

3. WHAT IS CRYPTOGRAPHY?
 Cryptography is the science of using mathematics to encrypt
and decrypt data.
 Cryptographic algorithm – mathematical function used in
encryption/decryption.
 Security of encrypted data depends on-strength of
cryptographic algorithm & secrecy of the key.
3

4. TYPES OF CRYPTOGRAPHY
2 main types: Secret key & Public key.
o Secret key Cryptography:
o Public key Cryptography:
4

5. CRYPTANALYSIS ATTACKS
 Cipher-image-only attack (brute force).
 Known plain-image-only attack.
 Chosen-plain-image attack.
 Jigsaw puzzle attack.
 Neighbour attack. 5

6. WHY IMAGE CRYPTOSYSTEMS?
 Use of Images in Communication has increased
exponentially in past decade.
 The traditional cryptosystems cannot be used to encrypt
images directly for 2 reasons:
i. Image size is always much greater than that of text.
ii. The decrypted text must same as the original text.
However, this requirement is not necessary for image
data (little of distortion is allowed). 6

7. BASIC CHARACTERISTICS OF IMAGE
CRYPTOSYSTEMS
 System should be computationally secure.
 Encryption and decryption should be fast enough.
 The security mechanism should be widely acceptable
to design a cryptosystem like a commercial product.
 Also should be flexible.
7

8. CHALLENGES IN IMAGE ENCRYPTION
 The two main problems that arise in image encryption
process are with respect to:
o Computational time.
o Security level.
 Real time image encryption prefers ciphers that take
less amount of computational time without
compromising security. 8

9. PREVIOUS WORKS
 Encryption of binary and gray-scale images based on
SCAN patterns.
 It converts 2D images to 1D list & employs a SCAN
language to describe the converted result.
 Drawback:
i. Image compression is not considered.
ii. Computationally slow.
9

10.  Combinational Permutation Technique.
 Main idea here is that images can be viewed as an arrangement
of pixels, bits &blocks.
 Information in an image can be reduced by decreasing the
correlation among bits, pixels & blocks in a given arrangement
using different permutation operation.
 This method uses many keys selected using PRIG for different
permutation operation.
 Drawback: it provides security only against casual listeners.
10

11. ADVANCED ENCRYPTION STANDARD
 AES is a symmetric Encryption Algorithm.
 This algorithm uses a 128 bit data block and may use
three different key sizes 128, 196 and 256 bits.
 The 128 bit data block is divided into 16 bytes and are
mapped into a 4x4 array called State.
 It is an iterative algorithm.
 The total number of rounds Nr is dependent on Key
length Nk . 11

12. TABLE 1: AES PARAMETERS
Algorithm Key length,Nk Block size, Nb No of Rounds,
Nr=Nk+6
AES-128 4 4 10
AES-192 6 4 12
AES-256 8 4 14
Here, the length is specified in “words”.
AES operates on the: Binary Finite Field, GF(28).
Each byte will be represented as a polynomial of at most degree 7:
b7X7 + b6X6 + b5X5 + b4X4 + b3X3 + b2X2 + b1X1 + bo
12

13. AES ALGORITHM
13

14. a. 4 TRANSFORMATION IN AES
ENCRYPTION
1. Sub-Bytes: Operates independently on each byte
in the State and performs a non-linear substitution
from S-box.
 The S-box performs affine transformation on the
multiplicative inverse „x‟ for a byte „b‟ in GF(28) and
adds it with 63h( value of 99 in hex).
14

15. S(SUBSTITUTION)-BOX
15

16. S-1 box for inverse sub-byte transformation:
 It is calculated by first calculating the inverse affine
transformation of the input value, followed by the
multiplicative inverse.
 The inverse affine transformation is as follows:
16

17. 17
Figure: look up table for Inverse SubByte Transform

18. 2. Shift Rows:
It will not change the values, but will just change their order.
It does a left circular shift to each row as below:
Row 0  Shift 0; Row 1  Shift 1; Row 2  Shift 2;
Row 3  Shift 3;
State[0,0] State[0,1] State[0,2] State[0,3] State[0,0] State[0,1] State[0,2] State[0,3]
State[1,0] State[1,1] State[1,2] State[1,3] State[1,1] State[1,2] State[1,3] State[1,0]
State[2,0] State[2,1] State[2,2] State[2,3] State[2,2] State[2,3] State[2,0] State[2,1]
State[3,0] State[3,1] State[3,2] State[3,3] State[3,3] State[3,0] State[3,1] State[3,2]
18

19. 3. Mix Columns:
 It operates on individual columns of the state.
 The columns are considered as polynomials over GF(28) and
are multiplied with a mixing polynomial,
{03}*x3 + {01} * x2 + {01} * x + {02}.
 The result should be relatively prime with the polynomial
x4+1={11}=(x+1)4
 This can be represented by matrix equation:
19

20.  InvMixColumns can be described by the equation:
20

21. 4. Add Round Key:
 It is the step that incorporates the round key, a portion of the
expanded key, into the plaintext.
 This routine performs bitwise XOR of each byte of the state
with the corresponding byte of the round key.
 If Add Round Key operates on a variable twice, the variable
itself is returned.
21

22. b. KEY EXPANSION
 This routine expands the initial key to 4*(Nr+1) words.
 For Nk=4words, Nr=10; this routine creates 44 words.
 Process is as follows:
 First 4 words of round key are made from initial cipher key,
i.e., w[0]= k[0:3] ; w[1]=k[0:7] and so on.
 The rest of the words (wi for i=4 to 43) are derived as follows:
if (i mod 4)!=0 then, wi = wi-1+ wi-4 ;
else if (i mod 4)=0 then, temp = w[i-1];
temp = Sub Word (Rot Word (temp)) + Rcon [i/4]; 22
w[i] = w[i-4] + temp;

23. operations performed to obtain wi when (i mod 4) = 0
i. RotWord: performs one byte circular left shift on wi-1.
ii. SubWord: performs a byte substitution on each byte of its
input word, using the S-box.
iii. The result of step (i) and (ii) is XORed with a round
constant Rcon[j].
Rcon[j]={RC[j],0,0,0},where RC[j]=2*RC[j-1].
j 1 2 3 4 5 6 7 8 9 10
RC[j] 01 02 04 08 10 20 40 80 1B 36
Table 2 : RC values in hex 23

24. MODIFICATION IN AES KEY EXPANSION
TO SUIT IMAGE ENCRYPTION
 The initial key is expanded based on the number of
pixels in the image.
 The Rcon value is not constant instead it is being
formed from the initial key itself.
 The S-box and Inverse S-box are not directly used in
this algorithm; instead we perform some circular shift
on the boxes based on the initial key.
24

25. The above changes in the algorithm can be represented as:
 Key Expansion for the image :
Consider a plain image of size mxn. We encrypt a set of
16 pixels (128 bits) using 2 round keys.
∴ No of keys to Encrypt the whole image N=2*{(m*n)/16}.
 Formation of Rcon values :
Rcon[0]=key[12:15]; Rcon[1]=key[4:7];
Rcon [2]=key[0 : 3]; Rcon [3]=key[8:11];
25

26.  Using Inverse S-Box for key expansion:
The „temp‟ value used in the algorithm is formed as follows,
temp = SubWord(RotWord(temp)) + InvSubWord(Rcon[i/4]);
 Shifting of S-box and Inverse S-box:
Sbox_offset = sum(key[0:15])mod256;
Inv_Sbox_offset = (sum(key[0:15])*mean(key[0:15]))mod256;
26

27. STEPS INVOLVED
1. Key Selection.
2. Generation of Multiple
Keys.
3. Encryption.
4. Decryption.
27

28. EXPERIMENTAL ANALYSIS
A. Key Space Analysis:
The proposed algorithm has a huge key space of 2128 possible
keys.
Thus the key sensitivity of this algorithm is very high.
28

29. B. Histogram Analysis:
Figure 1(a): Lena Figure 1(b): Encrypted
Lena
29
Figure 1(c): Histogram of Figure 1(d): Histogram of
Lena Encrypted Lena

30. Figure 2(a): Mountains Figure 2(b): Encrypted
Mountain
30
Figure 2(c): Histogram of Figure 2(d): Histogram of
Mountain Encrypted Mountain

31. C. Key Sensitivity Analysis:
31

32. D. Execution Time:
Algorithm Time (in seconds)
Bourbakis(SCAN patterns) 2.54
Mitra (CPT) 1.82
Proposed Algorithm 1.41
Table 3: Computational Time for 1024x1024 Lena Image.
32

33. CONCLUSION
Based on the experimental results it can be observed that
 The proposed algorithm offers high encryption quality with
minimal computational time.
 The key sensitivity and key space of the algorithm is very
high which makes it resistant towards Brute force attack and
statistical cryptanalysis.
 The time taken for encryption is relatively less in comparison
with the algorithms proposed in the literature.
33

34. FUTURE WORK
 S-box is the pivotal part of AES. Research may be done
to improve the quality of S-box design.
 AES-192 or AES-256 may be used to further increase the
key sensitivity and key space of the algorithm.
34

35. REFERENCES
[1] B.Subramanyan, Vivek.M.Chhabria, T.G.Sankar babu, Image Encryption
Based On AES Key Expansion, 2011 Second International Conference on
Emerging Applications of Information Technology, page 217-220.
[2] N.J.Bourbakis , C.Alexopoulos, Picture data encryption using SCAN
patterns. Pattern Recognition 256 1992 pp567 -581.
[3] Mitra, Y. V. Subba Rao, and S. R. M. Prasanna, A new image encryption
approach using combinational permutation techniques, International Journal
of Computer Science, vol. 1, no. 2 , pp. 1306- 4428, 2006.
[4] http://en.wikipedia.org/wiki/Rijndael_S-box.
[5] http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf 35

36. 36