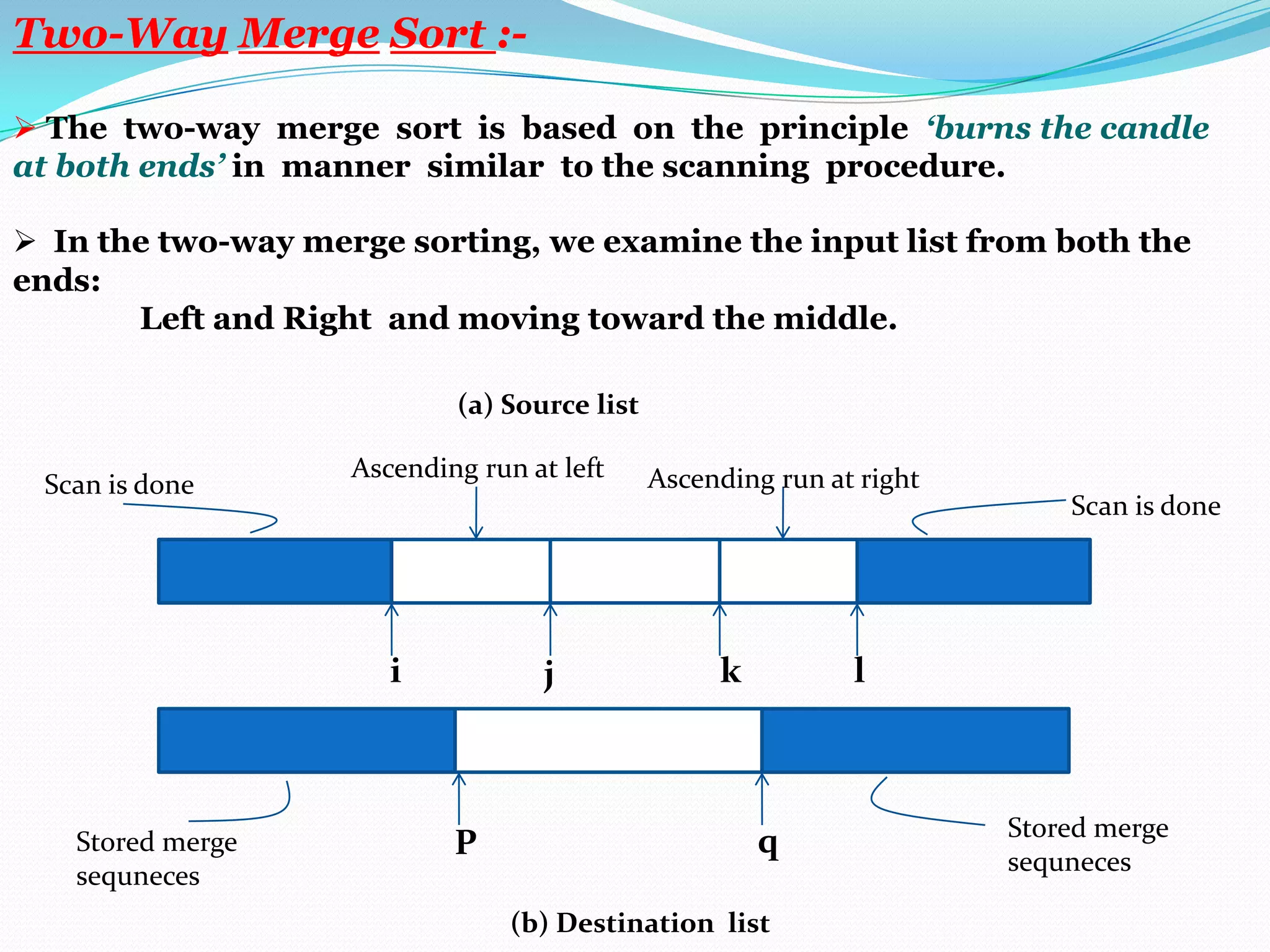
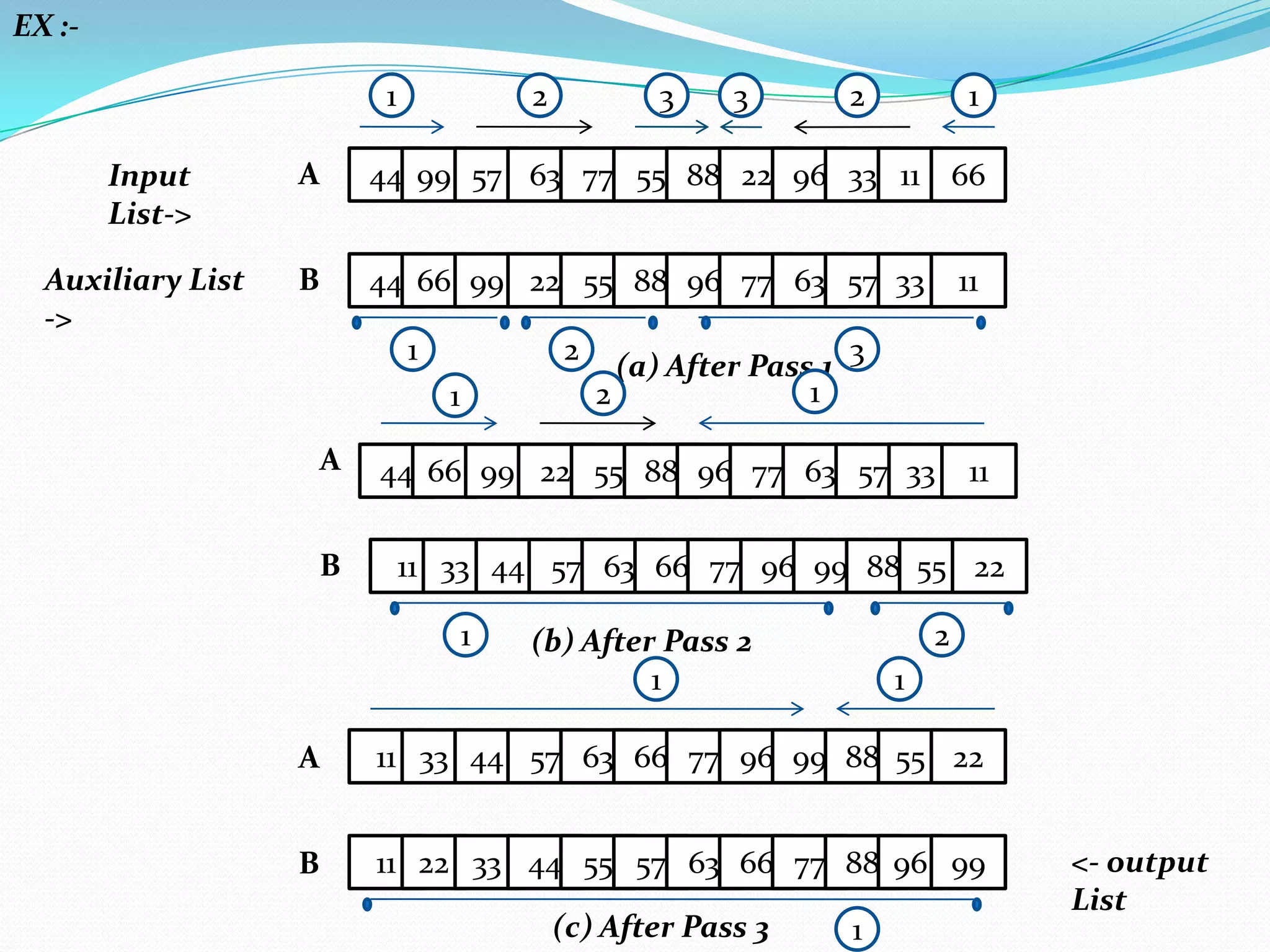
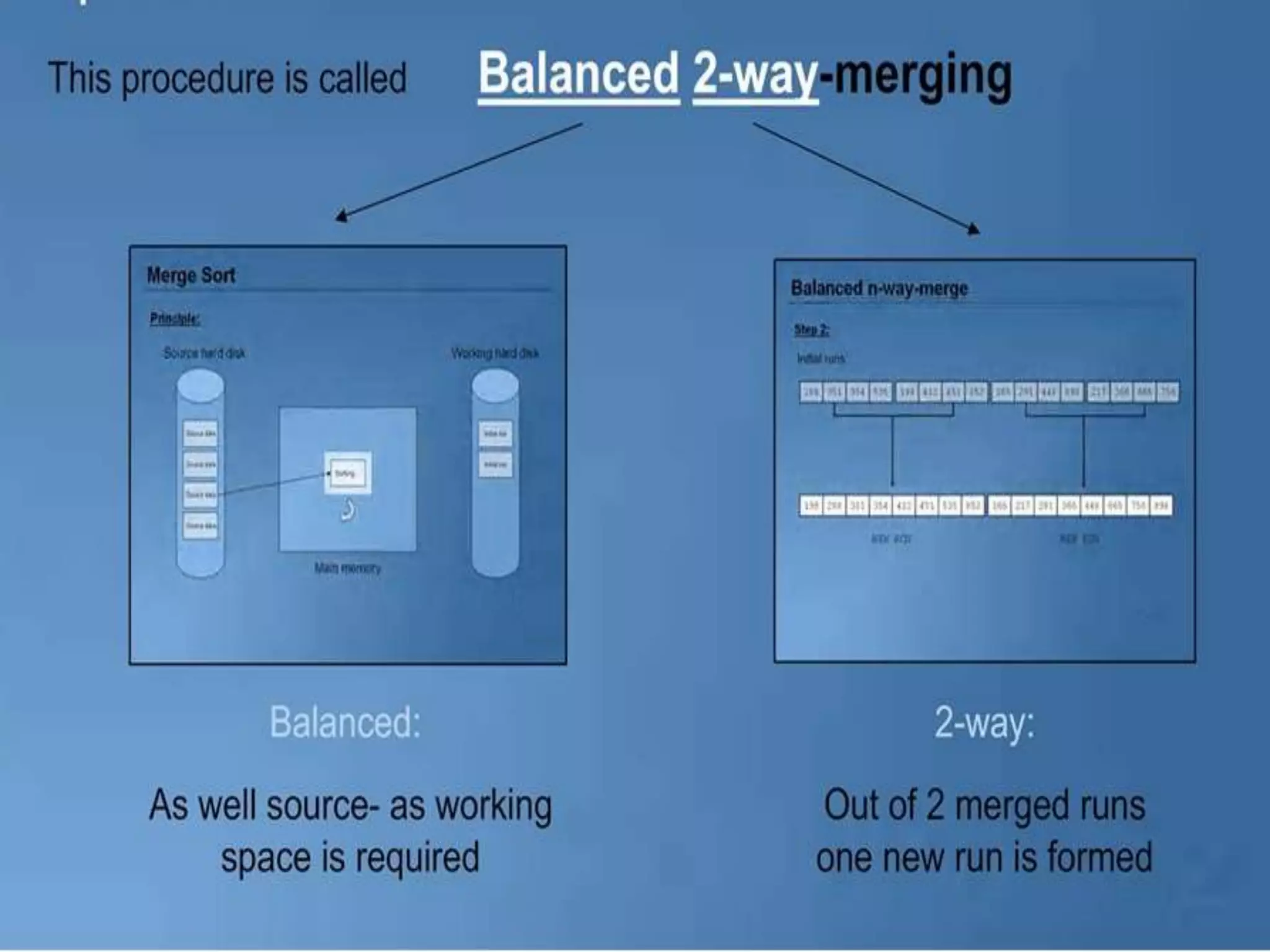
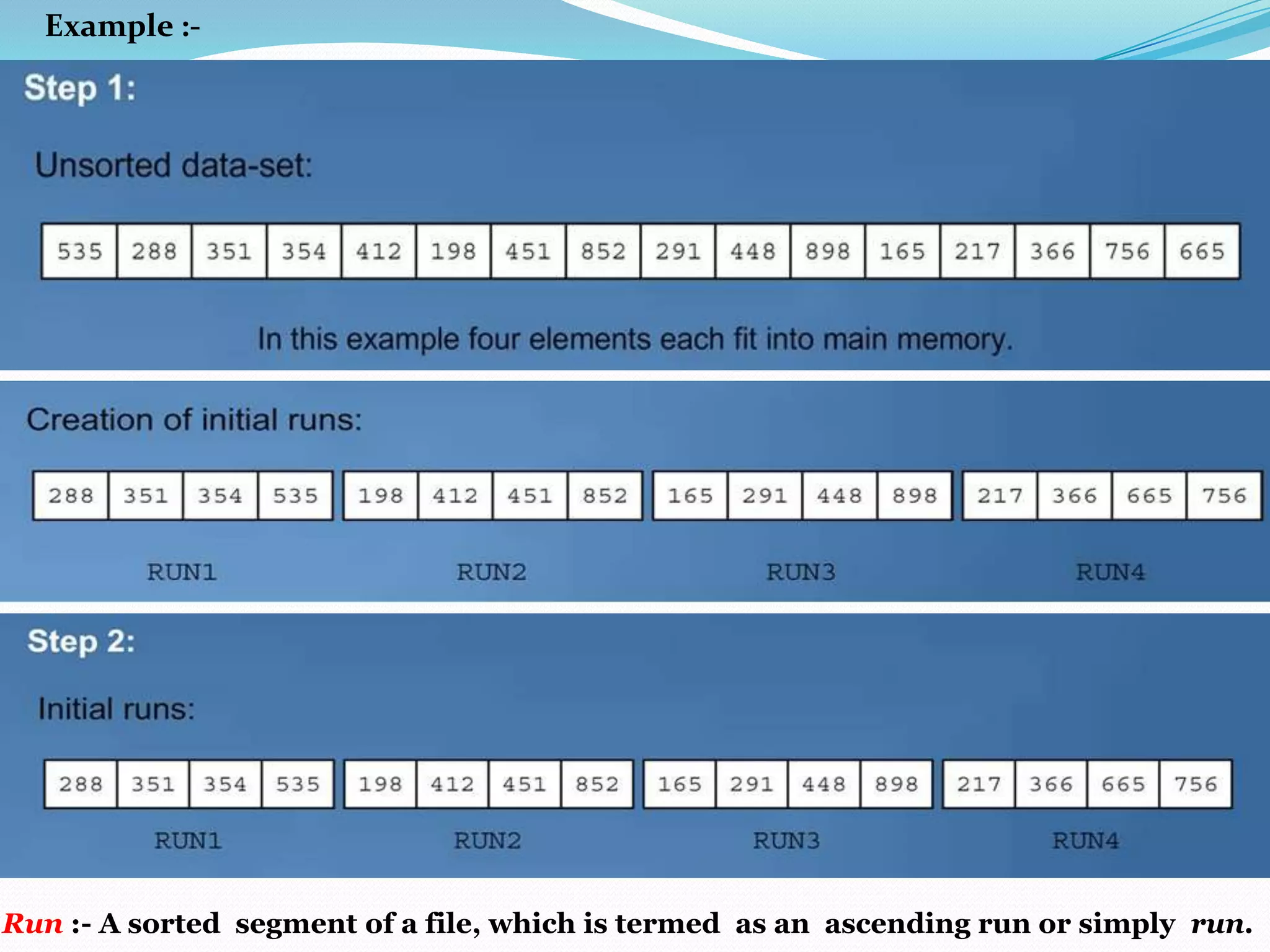
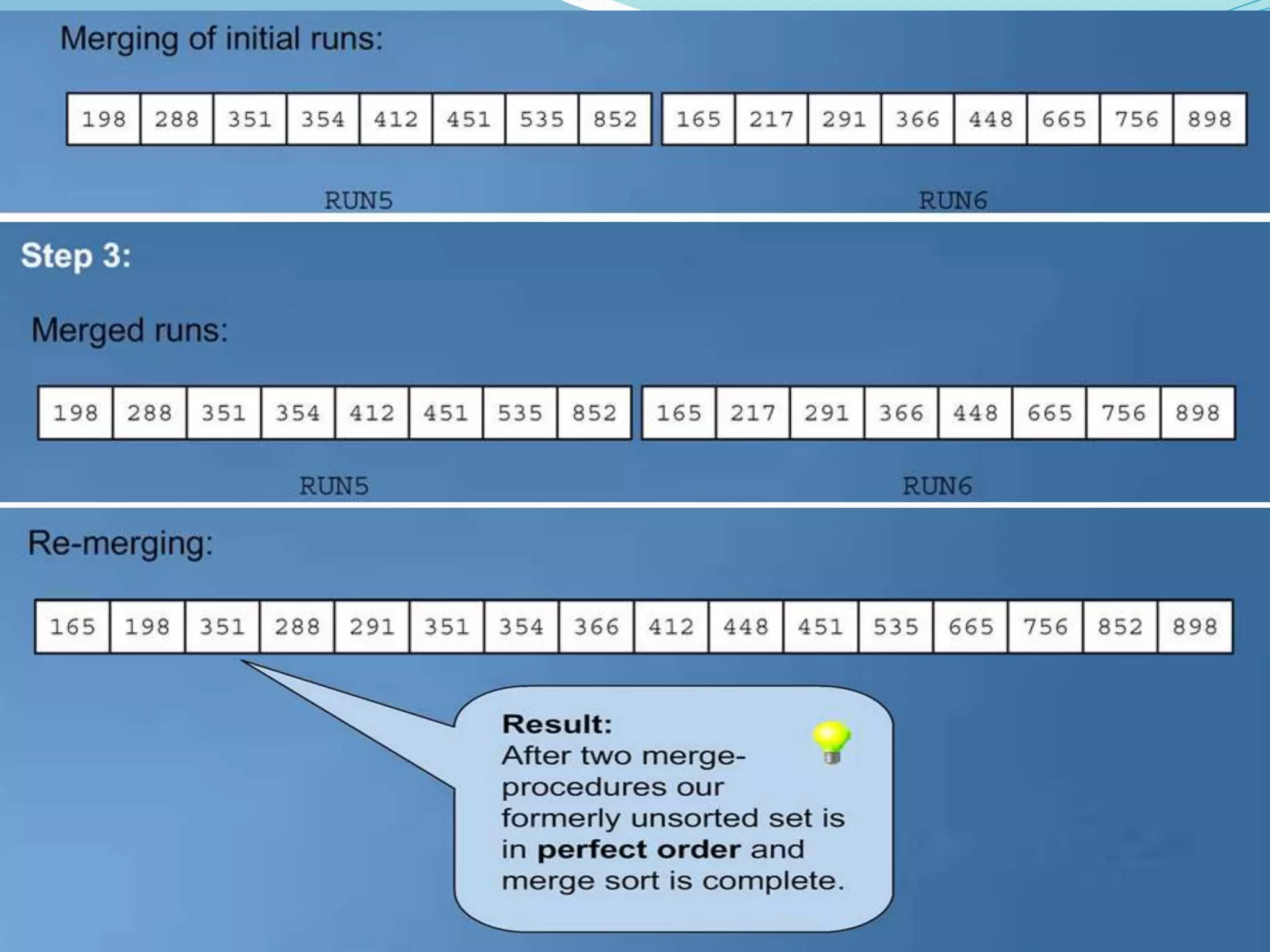
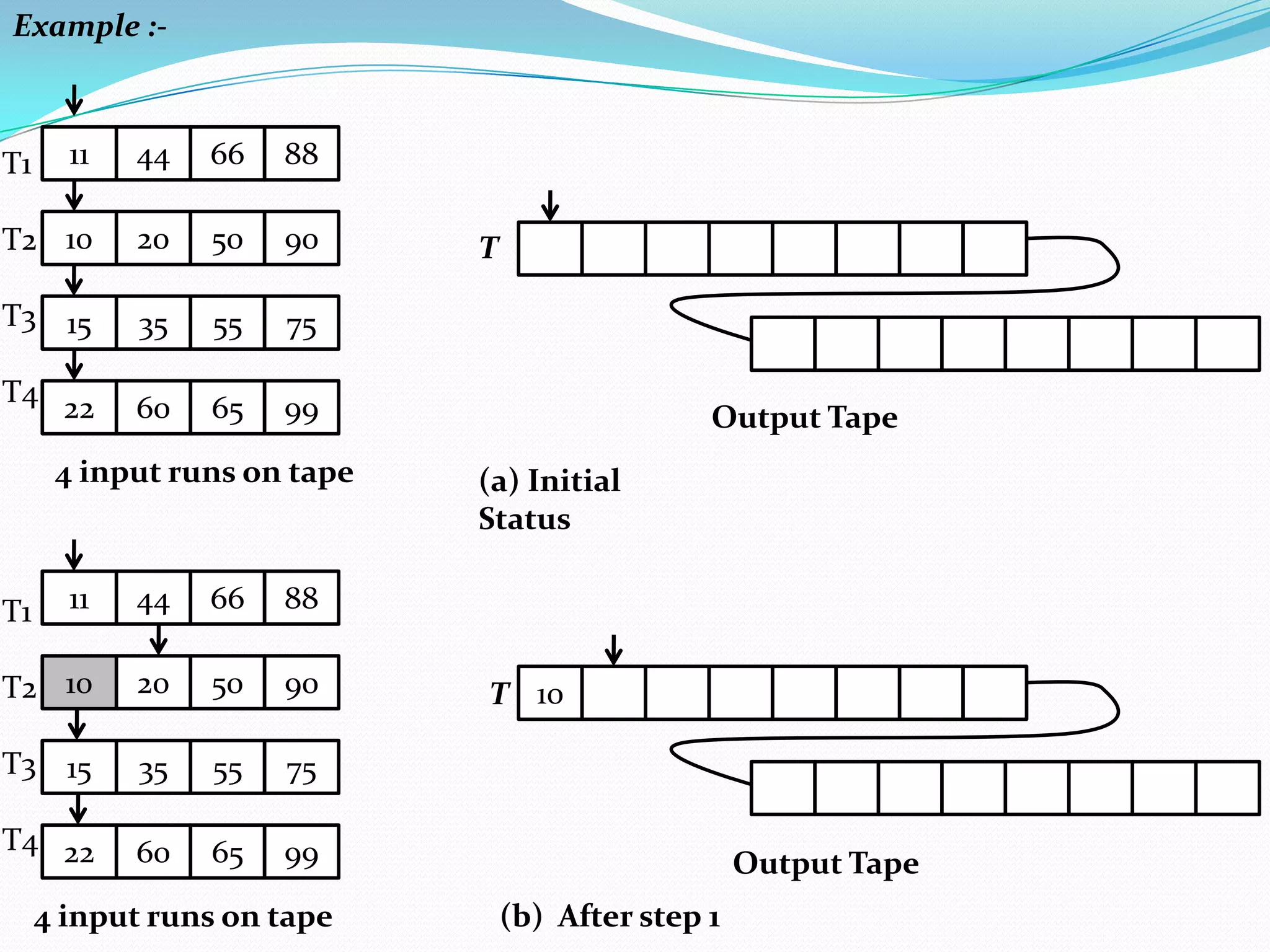
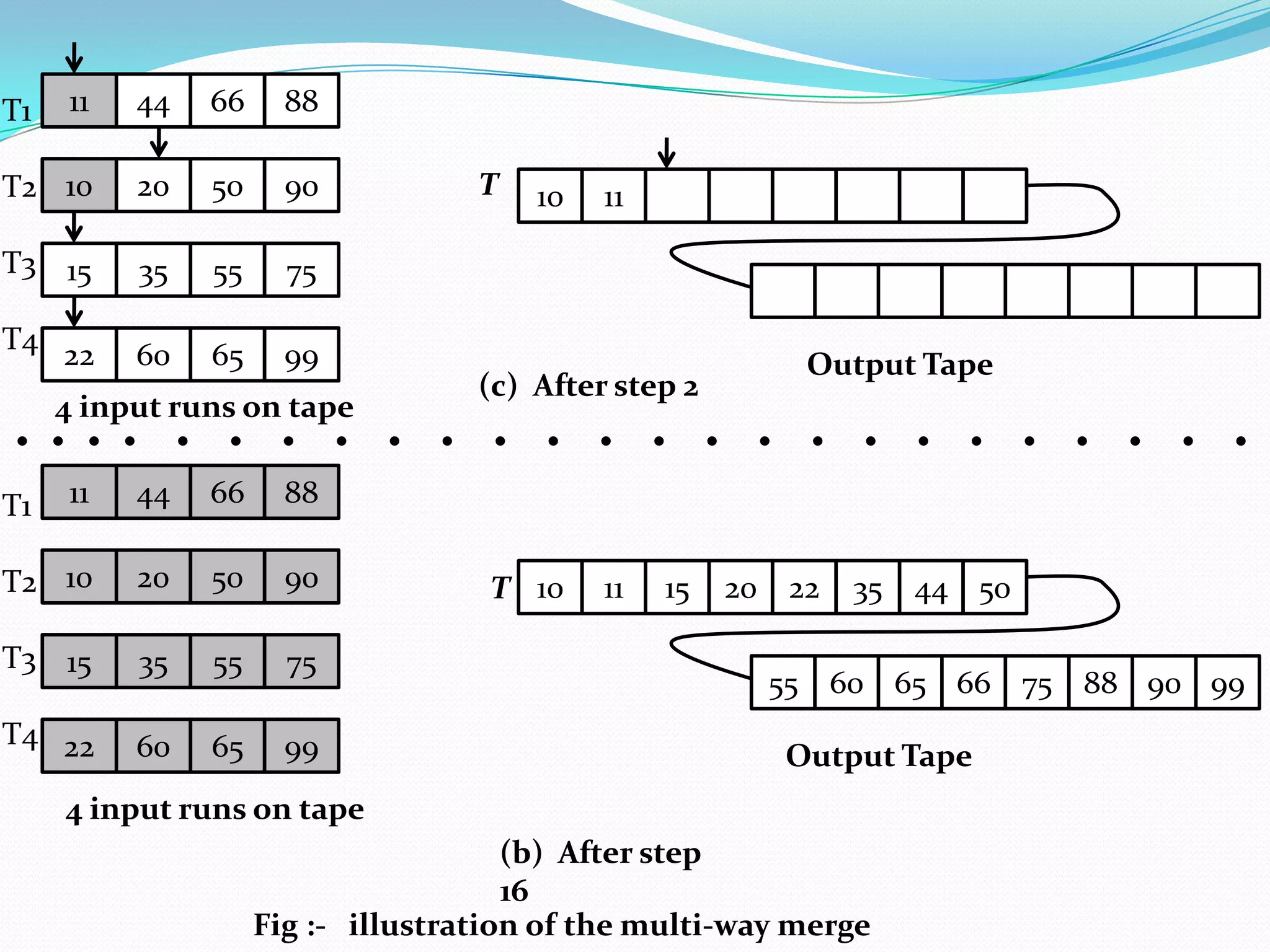
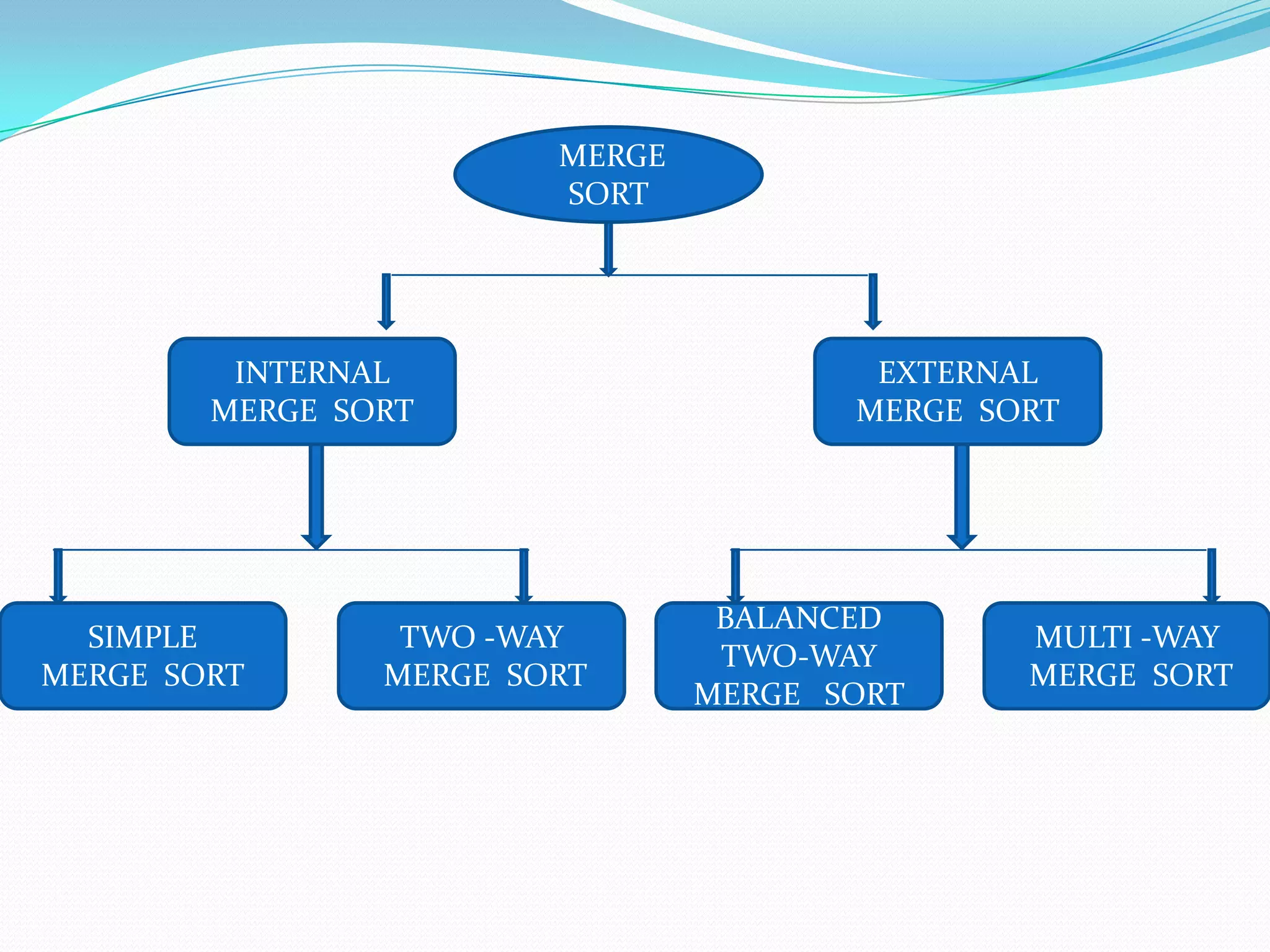
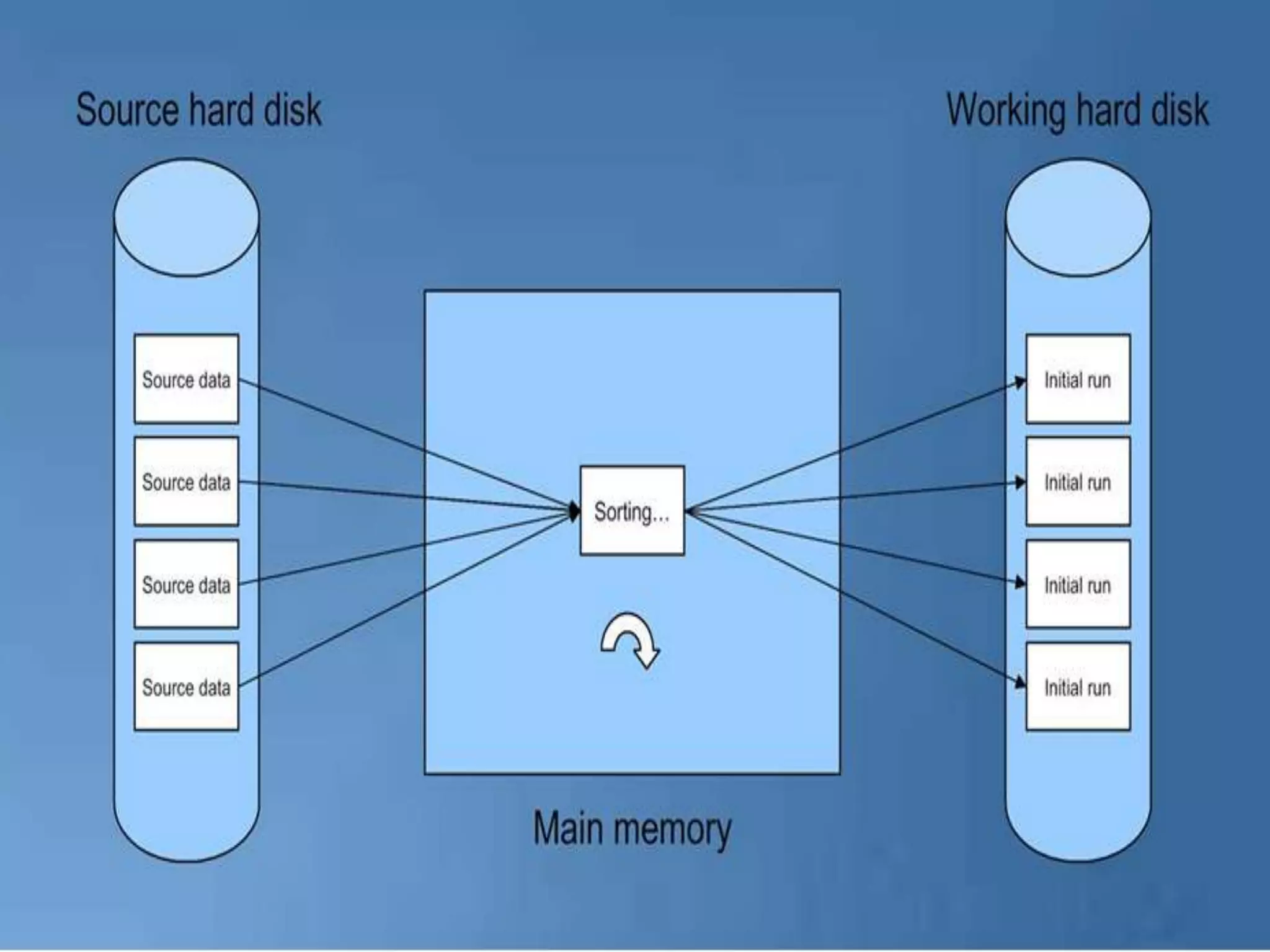
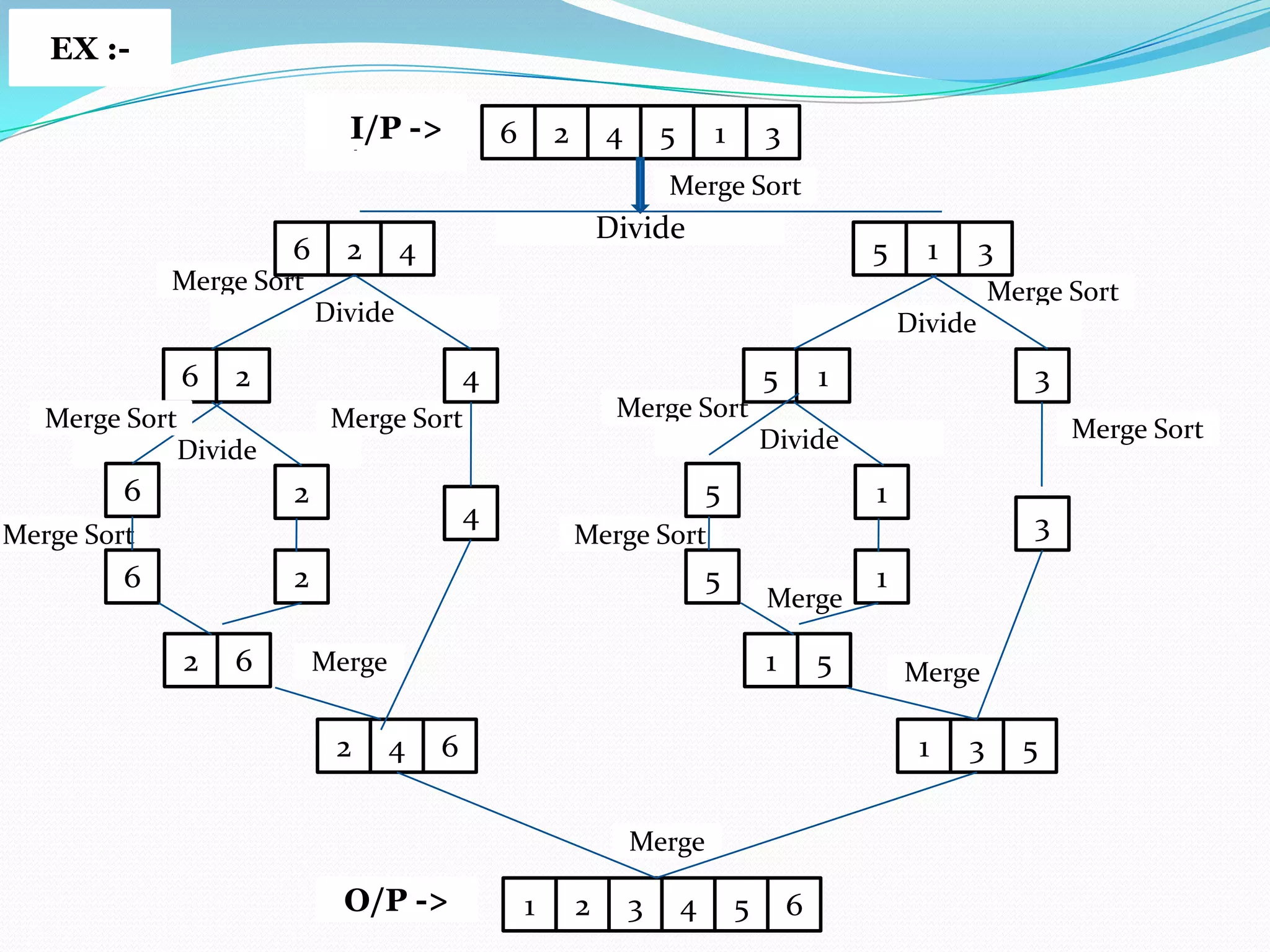
There are two broad categories of sorting methods based on merging: internal merge sort and external merge sort. Internal merge sort handles small lists that fit into primary memory, including simple merge sort and two-way merge sort. External merge sort is for very large lists that exceed primary memory, including balanced two-way merge sort and multi-way merge sort. The simple merge sort uses a divide-and-conquer approach to recursively split lists in half, sort each sublist, and then merge the sorted sublists.

1. ANKIT S. CHITNAVIS

2. MERGE SORT : All sorting method based on merging can be divided into
two broad categories :1. Internal merge sort
2. External merge sort.
 In internal merge sort , the lists under sorting are small and
assumed to be stored in the high speed primary memory.
 There are two type of Internal merge sort :I. Simple merge sort.
II. Two-way merge sort.

In external merge sort, deals with very large lists of elements
such that size of primary memory is not adequate to accommodate
the entire lists in it.
 There are two type of External merge sort :I. Balanced two-way merge sort.
II. Multi-way merge sort.

3. MERGE
SORT
INTERNAL
MERGE SORT
SIMPLE
MERGE SORT
TWO -WAY
MERGE SORT
EXTERNAL
MERGE SORT
BALANCED
TWO-WAY
MERGE SORT
MULTI -WAY
MERGE SORT

5. SIMPLE MERGE SORT : The simple merge sort (or merge sort) technique closely follows the
divide –and-conqure paradigm.
 let a list of n elements to be sorted with l and r being the position
of leftmost and rightmost element in the list.
 The three tasks in this divided-and-conqure technique are as
followed :-
[
]
1. Divide :- Partition the list midway ,that is ,at (l+r)/2 into two
sub lists with (n/2) elements in each, if n is even or
[n/2] and [n/2]-1 element if n is odd .
2. Conquer :- Sort the two lists recursively using the merge sort.
3. Combine :- Merge the sort sub listed to obtain the sorted output.

6. Combine
Conqure
Divide
l
r
.........................................................................
.
[(l+r)/2]
.................................. ..................................
.
.
Sort this left-part by merge sort Sort this right-part by merge sort
...................................
...................................
Merge the two list
Sorted List
Fig. Divide-and-conqure strategy in the merge
sort

7. EX :I/P ->
I/P ->
6
2
4
5
1
3
Merge Sort
6
2
Divide
4
5
1
3
Merge Sort
Merge Sort
Divide
6
Divide
2
4
Merge Sort
Divide
6
5
6
1
5
Merge
1
Merge
2
4
5
6
3
1
Merge
1
Merge
O/P ->
Merge Sort
Merge Sort
2
2
3
Divide
4
Merge Sort
1
Merge Sort
Merge Sort
2
6
5
1
2
3
4
5
6
3
5

8. Algorithm Merge sort
Input :- An array A[l…r] where l and r are the lower and upper index
of A.
Output :- Array a[l…r] with all element arranged in ascending order .
Steps:
1. if(r<=l) then
2.
Return
3. else
4.
Mid=[(l+r)/2]
5.
MergeSort(A[l…mid])
6.
MergeSort(A[mid+1…r])
7.
Merge(A,L,mid,r)
8. Endif
9. Stop

9. Two-Way Merge Sort : The two-way merge sort is based on the principle ‘burns the candle
at both ends’ in manner similar to the scanning procedure.
 In the two-way merge sorting, we examine the input list from both the
ends:
Left and Right and moving toward the middle.
(a) Source list
Scan is done
Ascending run at left
i
Stored merge
sequneces
j
P
Ascending run at right
k
Scan is done
l
q
(b) Destination list
Stored merge
sequneces

10. EX :-
1
2
3
3
2
1
Input
List->
A
44 99 57 63 77 55 88 22 96 33 11 66
Auxiliary List
->
B
44 66 99 22 55 88 96 77 63 57 33
1
2
1
A
B
(a) After Pass 1
1
2
11
3
44 66 99 22 55 88 96 77 63 57 33
11
11 33 44 57 63 66 77 96 99 88 55 22
1
2
(b) After Pass 2
1
1
A
11 33 44 57 63 66 77 96 99 88 55 22
B
11 22 33 44 55 57 63 66 77 88 96 99
(c) After Pass 3
1
<- output
List

11. BALANCED TOW-WAY MERGE SORT :-
 The balanced two-way merge is based on combining two ascending runs
into a single ascending run.
The merging-procedure can be applied to more than two runs at
each time.
 That why it is two way merging.
 In external balanced two-way merge all intial intial runs of equal
length possibly not the last run.
 This why the ‘ balanced’ tag is used in this technique.

13. Example :-
Run :- A sorted segment of a file, which is termed as an ascending run or simply run.

15. MULTI-WAY MEGRE SORT : In multi-way merge sort , this procedure is extended to m-way
merging , where m (m>2) runs are combined into a single run.
 In the multi-way merge sort , m input runs are stored on m tapes.
 Initially all element are in ascending order on all these tapes.
 In multi-way merge , we merge them together , that is ,we look at the
first element of each run and select the smallest element.
 This smallest element tranferred to an output tape.
This process is repeated till all runs are fully examined.

16. Example :-
11
44
66
88
T2 10
20
50
90
T3 15
35
55
75
T4 22
60
65
99
T1
4 input runs on tape
11
44
66
20
50
90
T3 15
35
55
60
65
(a) Initial
Status
75
T4 22
Output Tape
88
T2 10
T
99
T1
4 input runs on tape
T 10
Output Tape
(b) After step 1

17. 11
44
66
88
T2 10
20
50
90
T3 15
35
55
75
T4 22
60
65
99
T1
T
10
11
Output Tape
(c) After step 2
.... . . . . . . . . . . . . . . . . . . . . .
4 input runs on tape
11
44
66
88
T2 10
20
50
90
T3 15
35
55
75
T4 22
60
65
99
T1
T 10
11
15
20
22
35
44 50
55 60 65 66 75 88 90 99
Output Tape
4 input runs on tape
(b) After step
16
Fig :- illustration of the multi-way merge

18. THANK
YOU