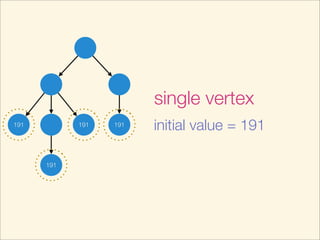
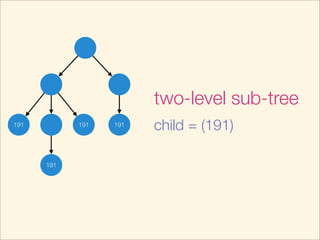
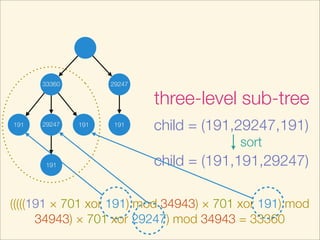
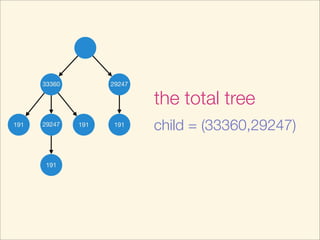
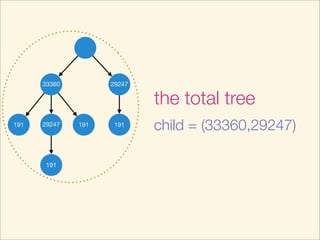
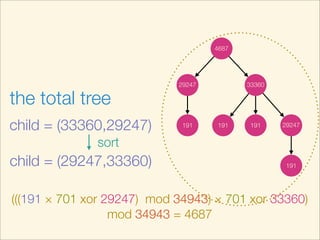
This document describes an algorithm for determining if two trees are isomorphic by hashing the trees. It hashes each subtree and sorts the hashes to get a unique representation of the tree. It recursively hashes subtrees from leaves to root. The hash of the whole tree represents the tree and trees are isomorphic if they have the same hash value. The time complexity is O(N log N) where N is the number of vertices. Pseudocode and examples are provided.

1. Tree Isomorphism
郭至軒（KuoE0）
KuoE0.tw@gmail.com
KuoE0.ch

2. Latest update: May 1, 2013
Attribution-ShareAlike 3.0 Unported
(CC BY-SA 3.0)
http://creativecommons.org/licenses/by-sa/3.0/

3. Isomorphism
The structures of two trees are equal.

4. so abstract...

5. 7
6 1 2
45 3
7
1
6
2
4 5 3
4
3 1
5
72 6
isomorphism

6. How to judge two rooted
tree are isomorphic?

8. If the trees are isomorphic, all their sub-trees are
also isomorphic.

9. If the trees are isomorphic, all their sub-trees are
also isomorphic.

10. If the trees are isomorphic, all their sub-trees are
also isomorphic.

11. If the trees are isomorphic, all their sub-trees are
also isomorphic.

12. Hash the tree

13. Hash all sub-tree

14. Hash all sub-tree
recursively

15. initial value = 191
single vertex

16. initial value = 191
single vertex

17. initial value = 191
single vertex
191 191
191
191

18. initial value = 191
single vertex
191 191
191
191
define by yourself

19. 191 191
191
191
two-level sub-tree
child = (191)

20. 191 191
191
191
two-level sub-tree
child = (191)

21. 191 191
191
191
two-level sub-tree
child = (191)
(191 × 701 xor 191) mod 34943 = 29247
29247
29247

22. 191 191
191
191
two-level sub-tree
child = (191)
(191 × 701 xor 191) mod 34943 = 29247
29247
29247
define by yourself

23. 191 191
191
191
two-level sub-tree
child = (191)
(191 × 701 xor 191) mod 34943 = 29247
29247
29247
define by yourself

24. 29247
29247191 191
191
191
three-level sub-tree
child = (191,29247,191)

25. 29247
29247191 191
191
191
three-level sub-tree
child = (191,29247,191)

26. 29247
29247191 191
191
191
three-level sub-tree
child = (191,29247,191)
child = (191,191,29247)
sort

27. 29247
29247191 191
191
191
three-level sub-tree
child = (191,29247,191)
child = (191,191,29247)
sort
(((((191 × 701 xor 191) mod 34943) × 701 xor 191) mod
34943) × 701 xor 29247) mod 34943 = 33360
33360

28. 29247
29247191 191
191
191
three-level sub-tree
child = (191,29247,191)
child = (191,191,29247)
sort
(((((191 × 701 xor 191) mod 34943) × 701 xor 191) mod
34943) × 701 xor 29247) mod 34943 = 33360
33360

29. 33360 29247
29247191 191
191
191
the total tree
child = (33360,29247)

30. 33360 29247
29247191 191
191
191
the total tree
child = (33360,29247)

31. 33360 29247
29247191 191
191
191
the total tree
child = (33360,29247)
child = (29247,33360)
sort

32. 33360 29247
29247191 191
191
191
the total tree
child = (33360,29247)
child = (29247,33360)
sort
(((191 × 701 xor 29247) mod 34943) × 701 xor 33360)
mod 34943 = 4687
4687

33. 33360 29247
29247191 191
191
191
the total tree
child = (33360,29247)
child = (29247,33360)
sort
(((191 × 701 xor 29247) mod 34943) × 701 xor 33360)
mod 34943 = 4687
4687

34. hash value of the
tree is 4687

35. initial value = 191
single vertex

36. initial value = 191
single vertex

37. initial value = 191
single vertex
191191
191
191

38. 191191
191
191
two-level sub-tree
child = (191)

39. 191191
191
191
two-level sub-tree
child = (191)

40. 191191
191
191
two-level sub-tree
child = (191)
(191 × 701 xor 191) mod 34943 = 29247
29247
29247

41. 191
29247
29247191
191
191
three-level sub-tree
child = (191,191,29247)

42. 191
29247
29247191
191
191
three-level sub-tree
child = (191,191,29247)

43. 191
29247
29247191
191
191
three-level sub-tree
child = (191,191,29247)
child = (191,191,29247)
sort

44. 191
29247
29247191
191
191
three-level sub-tree
child = (191,191,29247)
child = (191,191,29247)
(((((191 × 701 xor 191) mod 34943) × 701 xor 191) mod
34943) × 701 xor 29247) mod 34943 = 33360
sort
33360

45. 191
3336029247
29247191
191
191
the total tree
child = (33360,29247)

46. 191
3336029247
29247191
191
191
the total tree
child = (33360,29247)

47. 191
3336029247
29247191
191
191
the total tree
child = (33360,29247)
child = (29247,33360)
sort

48. 191
3336029247
29247191
191
191
the total tree
child = (33360,29247)
child = (29247,33360)
sort
(((191 × 701 xor 29247) mod 34943) × 701 xor 33360)
mod 34943 = 4687
4687

49. hash value of the
tree is 4687

51. ≡

52. Algorithm
HASH_TREE(T):
1. hash all sub-trees
2. sort hash value of sub-trees (unique)
3. calculate hash value (any hash function)

53. Time Complexity
O(Nlog2N)
N is number of vertices
height of tree

54. Source Code
int hash( TREE &now, int root ) {
int value = INIT;
vector< int > sub;
//get all hash value of subtree
for ( int i = 0; i < now[ root ].size(); ++i )
sub.push_back( hash( now, now[ root ]
[ i ] ) );
//sort them to keep unique order
sort( sub.begin(), sub.end() );
//hash this this tree
for ( int i = 0; i < sub.size(); ++i )
value = ( ( value * P1 ) ^ sub[ i ] ) % P2;
return value % P2;
}

55. Representation of Tree
Let the height of left child less than the right one.

56. Representation of Tree
Let the height of left child less than the right one.

57. 4
3 2
121 1
1

58. 3
21 1
1
4
3 2
121 1
1
4
2
1

59. 2
1
3
21 1
1
4
3 2
121 1
1
4
2
1
3
1 1
4
2
1

60. Algorithm
SORT_CHILD(T):
1. sort all sub-trees
2. compare the height
3. if height is equal, compare child
recursively
4. put the lower at left and the higher at
right

61. How about unrooted tree?

62. Find a Root

63. eliminate leaves

64. eliminate leaves

65. eliminate leaves

66. eliminate leaves

67. eliminate leaves

68. eliminate leaves

69. Enumerate Possible Root(s)

70. Rebuild The Tree

71. Rebuild The Tree

72. Rebuild The Tree

73. Rebuild The Tree

74. Rebuild The Tree

75. Rebuild The Tree

76. Apply the Isomorphism Detection

77. [POJ] 1635 - Subway tree systems
Practice Now

78. ThankYou forYour Listening.