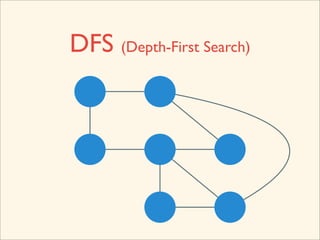
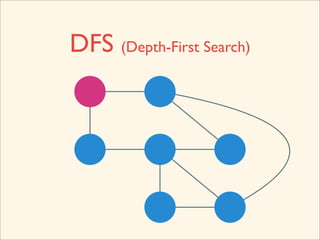
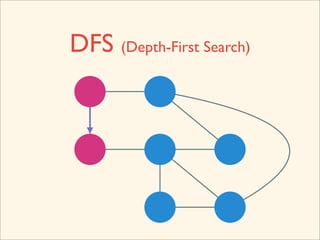
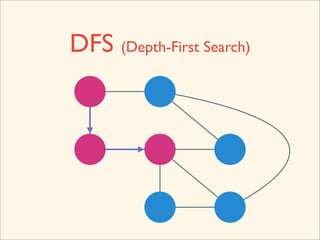
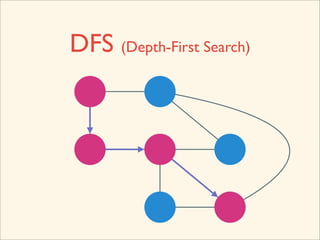
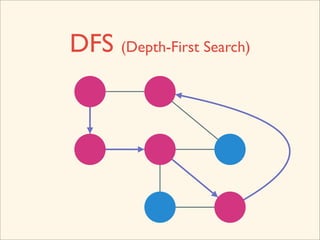
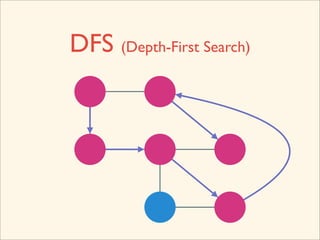
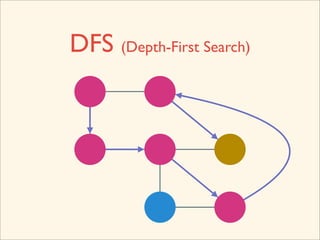
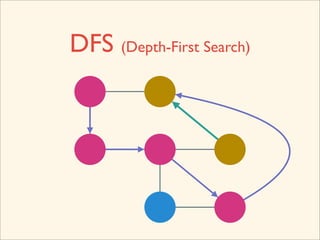
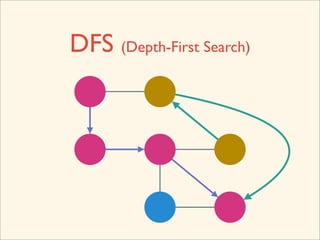
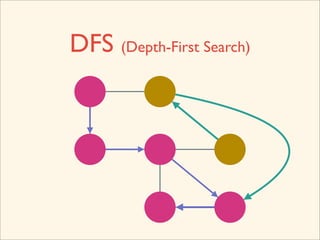
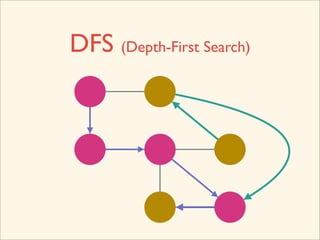
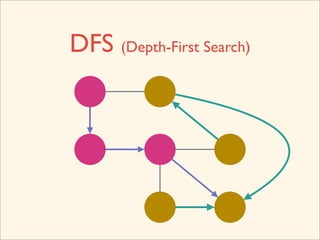
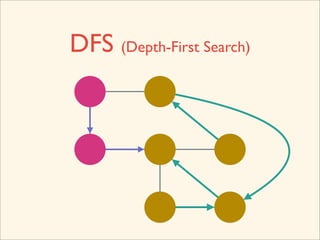
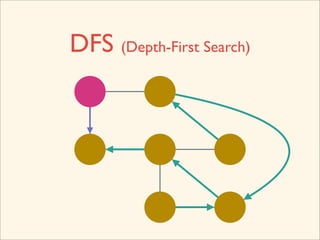
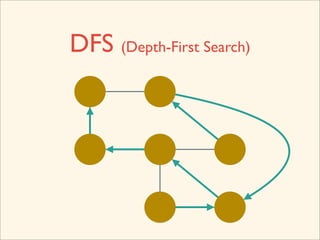
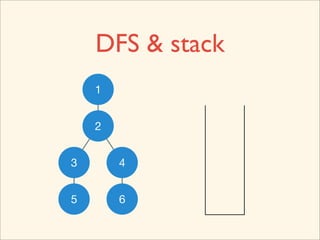
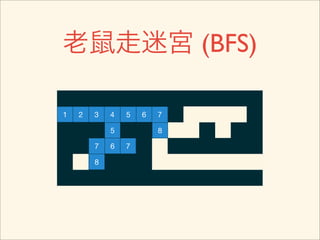
The document discusses graph traversal algorithms depth-first search (DFS) and breadth-first search (BFS). It provides examples of how DFS and BFS traverse graphs using a stack and queue respectively. Pseudocode for DFS and BFS algorithms is presented. The time complexity of both algorithms is O(V+E) where V is the number of nodes and E is the number of edges. Examples of DFS and BFS traversing a mouse maze are also shown.

1. Traversal
郭至軒（KuoE0）
KuoE0.tw@gmail.com
KuoE0.ch

2. Attribution-ShareAlike 3.0 Unported
(CC BY-SA 3.0)
http://creativecommons.org/licenses/by-sa/3.0/
Latest update: Mar 13, 2013

3. Graph

4. Traversal

5. Traversal

6. DFS (Depth-First Search)

7. DFS (Depth-First Search)

8. DFS (Depth-First Search)

9. DFS (Depth-First Search)

10. DFS (Depth-First Search)

11. DFS (Depth-First Search)

12. DFS (Depth-First Search)

13. DFS (Depth-First Search)

14. DFS (Depth-First Search)

15. DFS (Depth-First Search)

16. DFS (Depth-First Search)

17. DFS (Depth-First Search)

18. DFS (Depth-First Search)

19. DFS (Depth-First Search)

20. DFS (Depth-First Search)

21. DFS (Depth-First Search)

22. DFS & stack
1
2
3 4
5 6

23. DFS & stack
1
2
3 4
5 6 1

24. DFS & stack
1
2
3 4
2
5 6 1

25. DFS & stack
1
2
3 4 3
2
5 6 1

26. DFS & stack
1
2
5
3 4 3
2
5 6 1

27. DFS & stack
1
2
3 4 3
2
5 6 1

28. DFS & stack
1
2
3 4
2
5 6 1

29. DFS & stack
1
2
3 4 4
2
5 6 1

30. DFS & stack
1
2
6
3 4 4
2
5 6 1

31. DFS & stack
1
2
3 4 4
2
5 6 1

32. DFS & stack
1
2
3 4
2
5 6 1

33. DFS & stack
1
2
3 4
5 6 1

34. DFS & stack
1
2
3 4
5 6

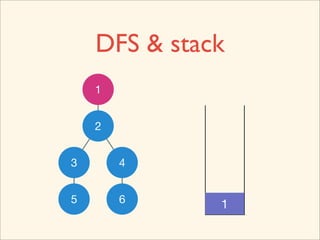
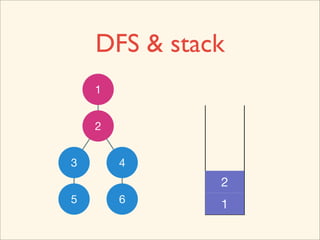
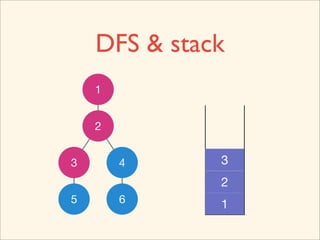
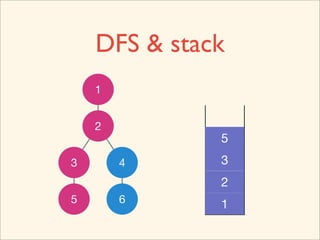
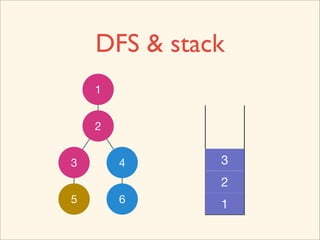
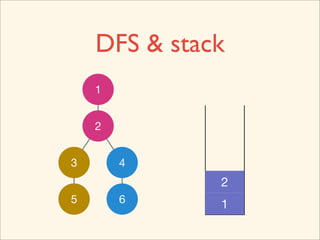
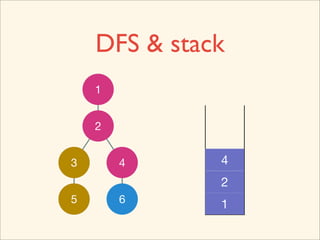
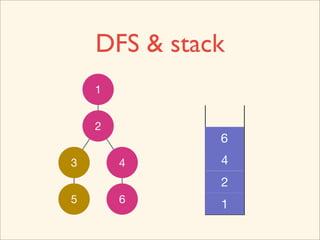
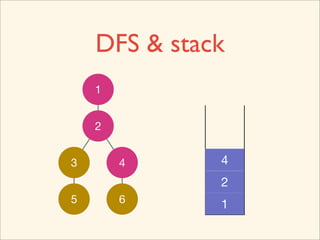
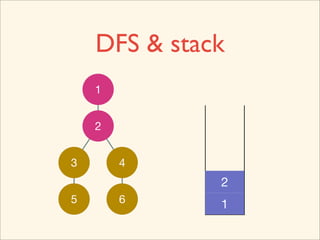
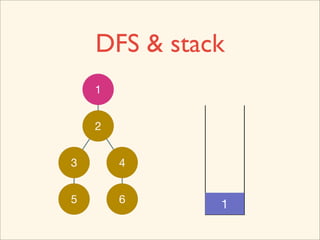
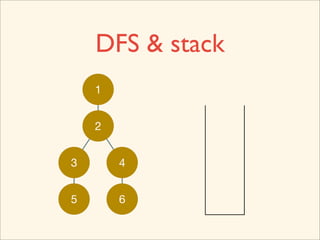
35. Source Code
// There are n nodes.
// g is an adjacent matrix.
void DFS( int now ) {
if ( visited[ now ] == true )
return;
visited[ now ] = true;
for ( int i = 0; i < n; ++i ) {
if ( g[ now ][ i ] == true )
DFS( i );
}
return;
}

36. Source Code
// There are n nodes.
// g is an adjacent matrix.
void DFS() {
stack< int > stk;
stk.push( 0 );
while ( stk.empty() != true ) {
int now = stk.top();
visited[ now ] = true;
bool noleaf = true;
for ( int i = 0; i < n; ++i )
if ( g[ now ][ i ] == true && visited[ i ] != true ) {
stk.push( i );
noleaf = false;
break;
}
if ( noleaf == true )
stk.pop();
}
}

37. BFS (Breadth-First Search)

38. BFS (Breadth-First Search)

39. BFS (Breadth-First Search)

40. BFS (Breadth-First Search)

41. BFS (Breadth-First Search)

42. BFS & queue
1
2
3 4
5 6

43. BFS & queue
1 1
2
3 4
5 6

44. BFS & queue
1 1
2
3 4
5 6

45. BFS & queue
1 1 2
2
3 4
5 6

46. BFS & queue
1 2
2
3 4
5 6

47. BFS & queue
1 2
2
3 4
5 6

48. BFS & queue
1 2 3
2
3 4
5 6

49. BFS & queue
1 2 3 4
2
3 4
5 6

50. BFS & queue
1 3 4
2
3 4
5 6

51. BFS & queue
1 3 4
2
3 4
5 6

52. BFS & queue
1 3 4 5
2
3 4
5 6

53. BFS & queue
1 4 5
2
3 4
5 6

54. BFS & queue
1 4 5
2
3 4
5 6

55. BFS & queue
1 4 5 6
2
3 4
5 6

56. BFS & queue
1 5 6
2
3 4
5 6

57. BFS & queue
1 5 6
2
3 4
5 6

58. BFS & queue
1 6
2
3 4
5 6

59. BFS & queue
1 6
2
3 4
5 6

60. BFS & queue
1
2
3 4
5 6

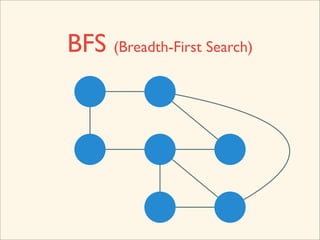
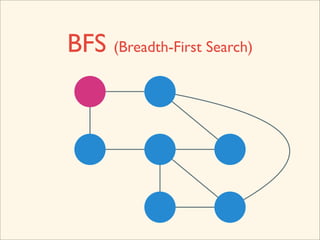
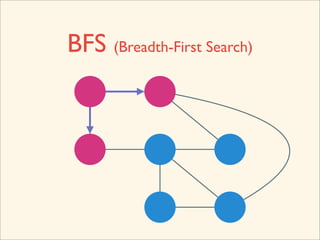
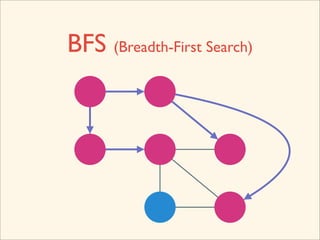
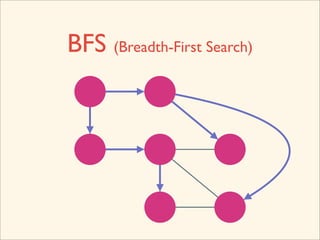
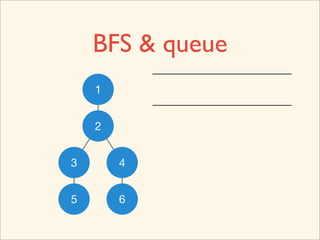
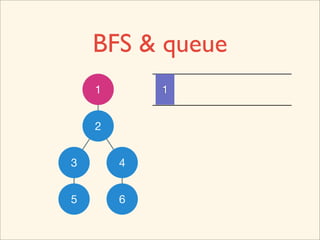
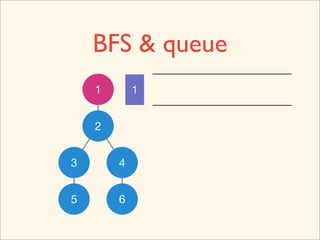
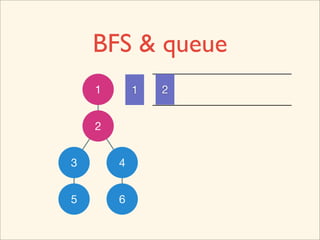
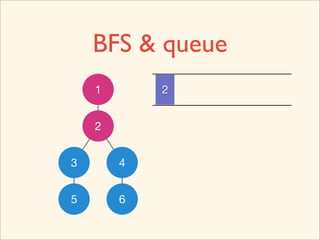
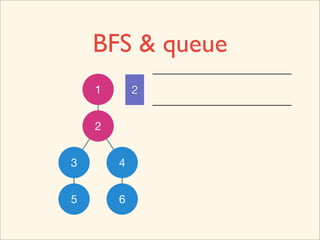
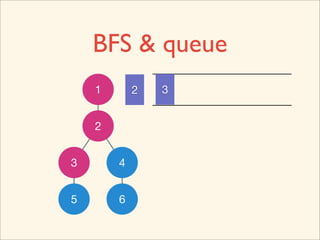
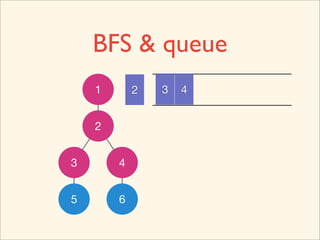
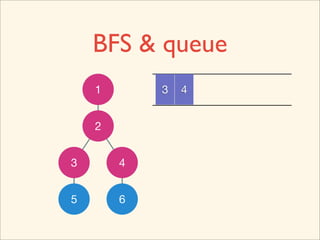
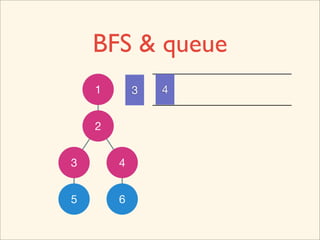
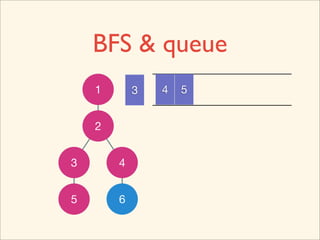
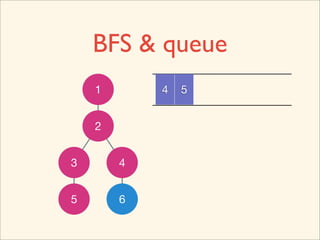
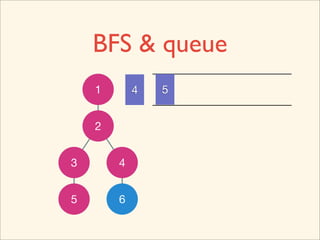
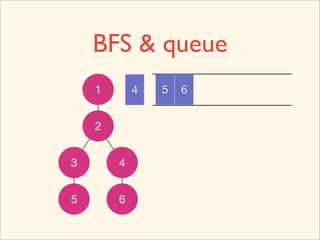
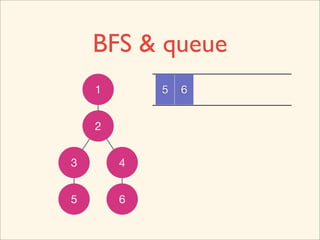
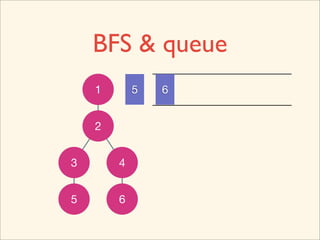
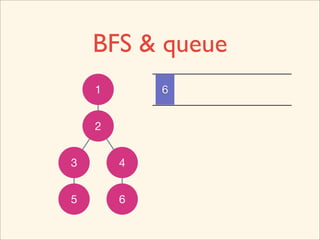
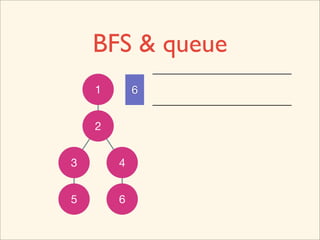
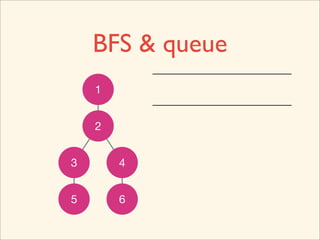
61. Source Code
// There are n nodes.
// g is an adjacent matrix.
void BFS() {
queue< int > que;
que.push( 0 );
while ( que.empty() != true ) {
int now = que.front();
que.pop();
visited[ now ] = true;
for ( int i = 0; i < n; ++i )
if ( g[ now ][ i ] == true )
que.push( i );
}
}

62. Time Complexity
DFS O(V+E)
BFS O(V+E)
V: the number of nodes
E: the number of edges

63. 老鼠走迷宮 (DFS)

64. 老鼠走迷宮 (DFS)

65. 老鼠走迷宮 (BFS)

66. 老鼠走迷宮 (BFS)
1

67. 老鼠走迷宮 (BFS)
1 2

68. 老鼠走迷宮 (BFS)
1 2 3

69. 老鼠走迷宮 (BFS)
1 2 3 4

70. 老鼠走迷宮 (BFS)
1 2 3 4 5
5

71. 老鼠走迷宮 (BFS)
1 2 3 4 5 6
5
6

72. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7
5
7 6 7

73. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7
5 8
7 6 7
8

74. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7
5 8 9
7 6 7 9
9 8

75. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7
5 8 9 10
7 6 7 9
9 8 10

76. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11
5 8 9 10
7 6 7 9
9 8 10 11

77. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12
5 8 9 10
7 6 7 9
9 8 10 11 12

78. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13
5 8 9 10
7 6 7 9
9 8 10 11 12 13

79. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14

80. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15

81. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

82. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

83. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

84. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

85. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

86. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

87. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

88. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

89. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

90. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

91. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

92. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

93. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

94. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

95. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

96. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

97. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

98. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

99. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

100. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

101. 老鼠走迷宮 (BFS)
1 2 3 4 5 6 7 11 12 13 14
5 8 9 10 14
7 6 7 9
9 8 10 11 12 13 14 15 16

102. Practice Now
[UVa] 352 - The Seasonal War

103. 352 - The Seasonal War
Sample Input Sample Output
6 Image number 1 contains 3 war eagles.
100100 Image number 2 contains 6 war eagles.
001010
000000
110000
111000
010100
8
01100101
01000001
00011000
00000010
11000011
10100010
10000001
01100000

104. 352 - The Seasonal War

105. 352 - The Seasonal War

106. 352 - The Seasonal War

107. 352 - The Seasonal War

108. Source Code
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n;
char map[ 30 ][ 30 ];
bool visited[ 30 ][ 30 ];
int step[ 8 ][ 2 ] = { { 1, 1 }, { 1, 0 }, { 1, -1 }, { 0, 1 },
{ 0, -1 }, { -1, 1 }, { -1, 0 }, { -1, -1 } };
void DFS( int r, int c );
int main() {
int t = 0;
while ( scanf( “%d”, &n ) != EOF ) {
int ret = 0;
for ( int i = 0; i < n; ++i )
scanf( “%s”, map[ i ] );
memeset( visited, 0, sizeof( visited ) );

109. Source Code
for ( int i = 0; i < n; ++i )
for ( int j = 0; j < n; ++j )
if ( map[ i ][ j ] == ‘1’ && visited[ i ][ j ] != true ) {
DFS( i, j );
++ret;
}
printf( “Image number %d contains %d war eagles.n”, ++t, ret );
}
return 0;
}
void DFS( int r, int c ) {
if ( visited[ r ][ c ] == true )
return;
visited[ r ][ c ] = true;
for ( int i = 0; i < 8; ++i ) {
int r2 = r + step[ i ][ 0 ], c2 = c + step[ i ][ 1 ];
if ( r2 >= 0 && r2 < n && c2 >= 0 && c2 < n && map[ r2 ][ c2 ]
== ‘1’ )
DFS( r2, c2 );
}
}

110. Practice Now
[UVa] 260 - Il Gioco dell'X

111. Thank You for Your Listening.