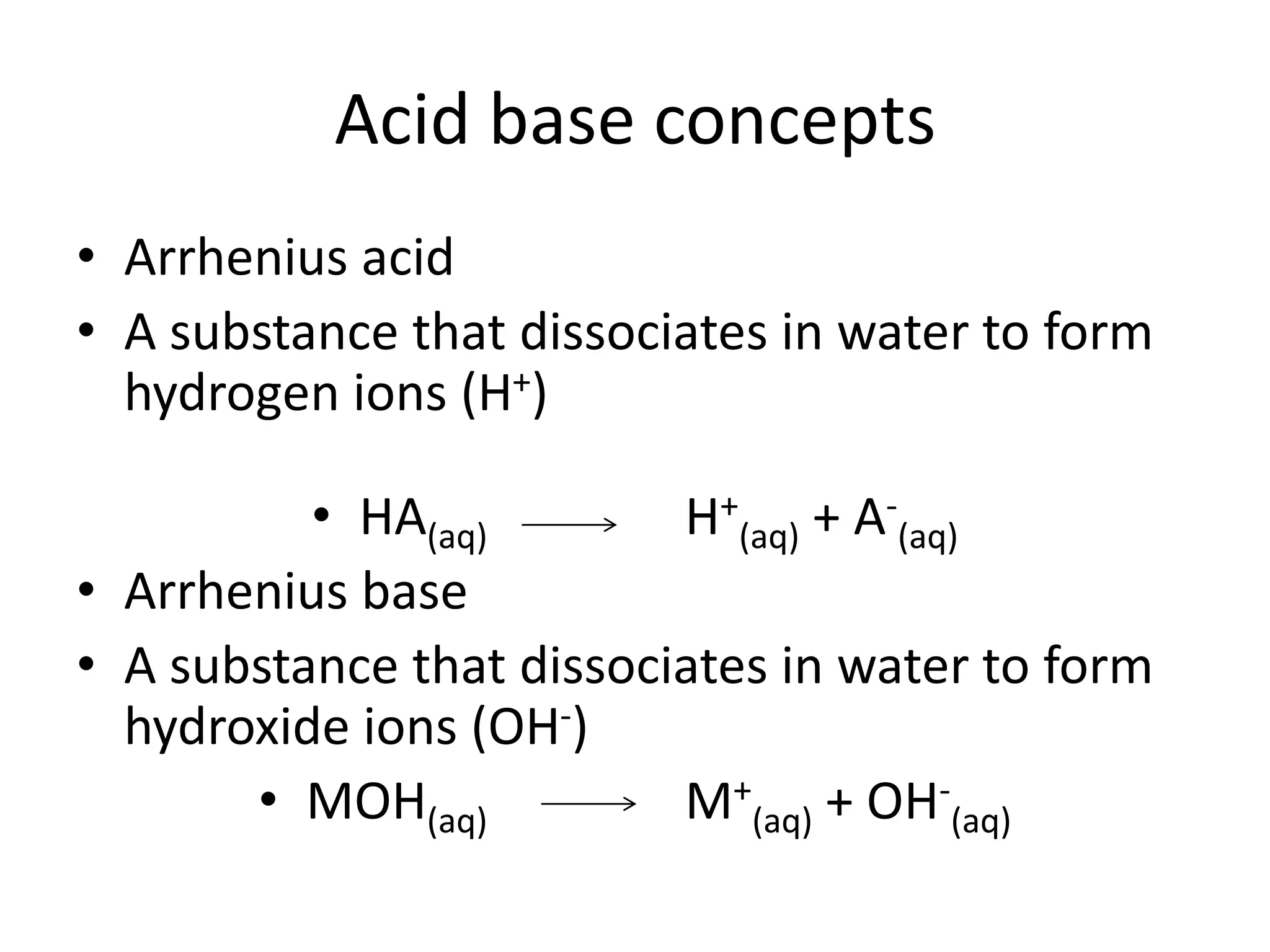
This document discusses acid-base concepts including: - Arrhenius and Bronsted-Lowry definitions of acids and bases - Conjugate acid-base pairs and the Lewis definitions - Acid-base reactions and the Brønsted-Lowry definitions of acids donating H+ and bases accepting H+ - Acid ionization constants (Ka) and base ionization constants (Kb) as well as the water autoionization constant (Kw) and how it relates to pH - Calculations involving pH, pOH, [H+], Ka, Kb, and the Henderson-Hasselbalch equation for buffer solutions

1. Acid base concepts
• Arrhenius acid
• A substance that dissociates in water to form
hydrogen ions (H+)
• HA(aq) H+
(aq) + A-
(aq)
• Arrhenius base
• A substance that dissociates in water to form
hydroxide ions (OH-)
• MOH(aq) M+
(aq) + OH-
(aq)

2. • Bronsted-lawry acid: a substance that can donate a proton H+
example:
HNO3 (aq) + H2O NO3
-
(aq) + H3O+
(aq)
• Bronsted-lawry base: a substance that can accept a proton H+
example:
NH3 (aq) + H2O NH4
+
(aq) + OH-
(aq)
• Chemical species whose formulas differ by only one proton are said to be:
conjugate acid base pairs

3. The Lewis Definitions of Acids and
Bases
• In the Lewis model, the H+ ion is the active
species it accepts a pair of electrons from the
OH- ion to form a covalent bond.
• bases donate pairs of electrons and acids
accept pairs of electrons

4. Acid-base reactions
• We are going to be working with acid-base
equilibria in aqueous solution, and we will use
the Brønsted-Lowry definitions that an acid is
a source of H+ and a base is an acceptor of H+.

5. Acid ionization constant Ka
The equilibrium constant is known as the acid
ionization constant Ka,
If Ka is much greater than 1, the acid is mostly dissociated and so is said to be a
strong acid. If Ka is much less than 1, the acid is dissociated only to a small extent
and so is said to be a weak acid.

6. Strong Acids
• Acids can be either strong or weak.
• A strong acid will completely ionize in water with one
product being (H+) aq (or H3O+) aq. (H+ and H3O+ are
two ways of writing the same idea.
HCl + H2O → H3O+ + Cl-
• Stronger acids produce higher concentrations of H3O+
than weak acids because of complete ionization.
• In addition, all strong acids are of the same strength if
they dissolved in equal molar concentration in water,
as they reach 100% ionization.
• There are seven strong acids: hydrochloric (HCl),
hydrobromic (HBr), hydroiodic (HI), nitric (HNO3),
perchloric (HClO4), and sulfuric (H2SO4).
6

7. Weak Acids

8. Base ionization constant Kb
• If Kb is much greater than 1, the base reacts nearly completely with water
and so is said to be a strong base. If Kb is much less than 1, the base reacts
hardly at all with water and so is said to be a weak base.

9. Water autoionization constant Kw
• water in one case plays the role of a base and
the other plays the role of an acid.

10. Water autoionization constant Kw
• This equation is called the autoionization of
water and its equilibrium constant is known as
the water autoionization constant Kw. At 25°C
it is equal to

11. Water autoionization constant Kw

12. Water autoionization constant Kw
• Because Kw is so small, water is ionized only
very slightly. We can compute the
concentration of H3O+ and OH- by solving the
autoionization equilibrium.

13. pH

14. [H+] pH
10-7 = 7
10-3 = 3
10-2 = 2
10-10 = 10
5x10-4 = 3.3
7x10-6 = 5.15
3.3x10-8 = 7.48
pH = -Log[H+]
It is easier to think in log
of concentrations but it
takes practice!!

15. Examples
• What is the Kb of the acetate anion? Ka= 1.75 x 10-5
Kw = KaKb ; Kb= Kw/Ka
Kb = 1x10-14/1.75x10-5
= 5.7x10-10
• What is the Kb of methylamine? Ka = 2.3x10-11
Kw = KaKb ; Kb= Kw/Ka
Kb = 1x10-14/2.3x10-11
= 4.3x10-4
• Which is the stronger base the acetate anion, or
methylamine? (methylamine)
15

16. pure strong acid (or base)
• HCl is a strong acid, with Ka = 107. What is the
pH of 10 M HCl?
The initial H3O+ = 10-7, due
to the autoionization of
water

17. PH of strong acids and bases
What is the pH of a 0.5 x10-7 M KOH solution?
KOH → K+ + OH-
Before dissociation 0.5 x10-7 M 0 0
After dissociation0 0 0.5 x10-7 0.5 x10-7 M
because it completely dissociates, so
[OH-] = 1x10-7 (from water) + 0.5 x10-7(from the base)
= 1.5 x10-7 M
pOH= -log (1.5 x10-7) = 6.82
pH = 14 - 6.82
= 7.18
17
In a solution strong acid that are less concentrated
than 1 * 10-6 M, is safer to assume that the
equilibrium concentration of H3O+ is equal to the
molar concentration of the acid + the H3O+
concentration from water.
[H+] = [H+] (from water) + [H+] (from the acid)
The same is true for the hydroxide concentration in
solution of strong base

18. PH of strong acids and bases
What is the pH of a 5.4x10-3 M solution of NaOH?
NaOH → Na+ + OH-
Before dissociation 5.4x10-3 M o 0
After dissociation 0 5.4x10-3 5.4x10-3 M
because it completely dissociates, so
[NaOH] = 0, [Na+] = 5.4x10-3, [OH-] = 5.4x10-3
pOH = -log 5.4x10-3 = 2.3
pH= 14- pOH
= 11.7
18

19. PH of Weak Acids
• Find the pH of a solution containing a weak
acid, say hydrofluoric acid, Ka = 6.8x10-4 at
0.05M concentration?
19

20. Answer
Ka= [H+][A-]/[HA]
HA ⇌ H+ + A-
Keq= [H+][A-]/[HA]
6.8 *10-4 = (x)(x) / (0.05)
X2= 6.8 *10-4 * 0.05
X= [H+]=[A-]= 0.00583
pH= -log[H+]= -log (0.00583) = 2.23
Initial 0.05 0 0
Equilibrium 0.05-x x x
After
Neglectance 0.05 x x
20

21. Keq value is very small
• For the initial dissociating compound:
Neglect x compared to CInitial (the initial
analytical concentration of the dissociating
compound) if:
1. CInitial ≥ 100 Keq in a dissociation reaction.
21

22. PH of Weak Bases
• What is the pH of a solution of 0.25M Triethylamine
(CH3CH2)3N, Ka = 1.93x10-11
22

23. Answer
Kw= Ka * Kb Kb= Kw/Ka= 1.0 * 10 -14 / 1.93x10-11 = 5.18 * 10-4
Kb= [BH+][OH-]/[B]
B + H2O ⇌ BH+ + OH-
Kb= [BH+][OH-]/[B]
5.18 * 10-4 = (x)(x) / (0.25)
X2= 5.18 * 10-4 * 0.25
X= [BH+]= [OH-]= 0.0114
pOH= -log[OH-]-log (0.0114) = 1.94 pH= 14 - 1.94= 12.06
Initial 0.25 0 0
Equilibrium 0.25-x x x
Neglect 0.25 x x
23

24. Buffers
• A buffer, is a solution that resists pH change, even
when strong acids or bases are added.
HA H+ + A-
• For the system above, the addition of A- creates a
solution with good concentrations of both A- and HA.
• When acid is added, the H+ reacts with A- to form
HA, and OH- (base) reacts with HA to form A-.
• Thus the addition of acid or base results in the
interconversion of HA and A-, but H+ changes in a
relatively minor fashion.

25. If you establish equilibrium, changes in [H+] will shift
the ratio of HA and A-.
By adding more H+ , A- will be consumed
forming HA.
If there is sufficient [A-], the extra H+ will also be
consumed and the [H+] will not change.



 A
H
HA

26. Buffer Solutions
Buffer-solution of weak acid or base and its salt
1. Acetic acid and sodium acetate (HA and A-)
HA ⇌ H+(aq) +A- (aq)
2. Ammonium chloride and ammonia (NH4
+ and NH3)
NH4
+(aq) ⇌ H+(aq) +NH3(aq)
3. KF and HF
4. But not HBr and KBr (HBr is a strong acid)
Major factor in biological systems
1. Blood pH= 7.35 - 7.45
2. Gastric juice pH= 1.5
26

27. Observation
If you add .01 ml i.e 1/100 ml of 1M HCl to 1000 ml
of water, the pH of the water drops from 7 to 5!!
i.e 100 fold increase in H+ concentration: Log = 2
change.
Problem:
Biological properties change with small changes in
pH, usually less than 1 pH unit.
How does a system prevent fluctuations in pH?

28. Buffers
A buffer can resist pH changes if the pH is at or near a weak
acid pK value.
Buffer range: the pH range where maximum resistance to pH
change occurs when adding acid or base. It is = +1 pH from
the weak acid pK
If pK is 4.8 the buffering range is 3.8 5.8

29. Henderson - Hasselbalch equation
]
[
]
][
[
HA
A
H
K



From
]
[
]
[
]
[ 


A
HA
K
H
Rearrange
Take (-)Log of each
]
[
]
[
log
log
HA
A
K
pH




]
[
]
[
log
HA
A
pK
pH




30. Above and below this range there is insufficient
amount of conjugate acid or base to combine with
the base or acid to prevent the change in pH.
[HA]
]
[A
log
pK
pH
-


1
10
10
1
from
varies
ratio
]
HA
[
]
[A



31. For weak acids
HA A- + H+
This equilibrium depends on concentrations of each component
.
If [HA] = [A-] or 1/2 dissociated
Then 0
1
log
]
[
]
[
log 


HA
A
By definition the pK is the pH where [HA] = [A-] :
50% dissociated
: pH = pK

32. You will be asked to solve Henderson -
Hasselbalch type problems:
You may be asked the pH, pK, the ratio of acid or base or solve for
the final concentrations of each.
also note : when [A-] > [HA] pH>pKa
when [A-] < [HA] pH <pKa
Exams Problems
[HA]
]
[A
log
pK
pH
-



33. The 6 step approach
1. Write the Henderson + Hasselbalch equation.
2. Write the acid base equation
3. Make sure either an H+ or OH- is in the equation.
3. Find out what you are solving for
4. Write down all given values.
5. Set up equilibrium conditions.
6. Plug in H + H equation and solve.

34. What is the pH of a solution of that contains 0.1M CH3C00-
and 0.9 M CH3C00H?
1) pH = pK + Log [A-]
[HA]
2) CH3C00H CH3C00- + H+
3) Find pH
4) pK = 4.76 A- = 0.1 M HA = 0.9 M
5) Already at equilibrium
6) X = 4.76 + Log 0.1
0.9
Log 0.111 = -.95 X = 4.76 + (-.95) X = 3.81

35. What would the concentration of CH3C00- be at pH 5.3
if 0.1M CH3C00H was adjusted to that pH.
1) pH = pK + Log [A-]
[HA]
2) CH3C00H CH3C00- + H+
3) Find equilibrium value of [A-] i.e [CH3C00-]
4) pH = 5.3; pK = 4.76
5) Let X = amount of CH3C00H dissociated at equilibrium
[A-] = [X]
[HA] = [0.1 - X]
6) 5.3 = 4.76 + Log [X]
[0.1 - X]
Now solve.

36. Problem?
• Mix 50 ml of 0.5M Sodium acetate with 25 ml of 0.1M
acetic acid , what is the pH of the resulting buffer
solution? Ka acetic acid = 1.8 *10-5
Answer
Total volume is 75 ml
pKa= -log (1.8 *10-5 ) = 4.757
Sodium acetate will ionize completely so: 0.5M Na+ and
0.5M acetate and acetate = A-
CH3COONa → Na+ + CH3COO-
36

37. Answer
Salt CH3COONa → Na+
+ CH3COO-
Cacetate
Acid CH3COOH ⇌ H+
+ CH3COO-
Initial CHA Cacetate
Equilibrium CHA - x x Cacetate + x
neglect CHA x Cacetate
Salt
Mol of Acetate = 0.05 L * 0.5 M = 0.025
Cacetate= mol / voltotal = 0.025 mol / (0.05 L+ 0.025 L) = 0.333 m
Acid
Mol of Acetic acid = 0.025 L * 0.1 M = 0.0025
CHA= mol / voltotal = 0.0025 mol / (0.05 L+ 0.025 L) = 0.0333 m
pH= pKa + log ([A-]/[HA]) pH= 4.757 + log ([0.333]/[0.0333])
pH= 5.757
A-
Simply, you can use the dilution law
C1V1=C2V2
37

38. Answer
We can solve the problem by another way
Ka= [H+][CH3COO-]/[CH3COOH]
1.8 *10-5 = [H+][ 0.333] / 0.0333
[H+]= 1.8 *10-5 * 0.0333 / 0.333
[H+]= 1.8 *10-6
pH= 5.757
38

39. Tolerance of a Buffer System
• If we need to check the stability of a buffer
system for any minor change in the buffer
acidity, basicity or system volume, then we
will examine the following cases.
• After calculation of the final concentration of
[HA] and [A-] after addition of acid or base
then the pH can be calculated by using
Henderson-Hasselbalch equation:
pH= pKa + log ([A-]/[HA])
39

40. Tolerance of a Buffer System:
Case#1
• Case #1
Start with 1 L of pure water and add 5 mL of 10M HCl. What would
be the initial and final pH?
• The initial pH for pure water = 7
• For the dilution of 5 mL of 10M HCl in 1 L of water, the final
volume of the solution will be 1.005 L.
C1V1=C2V2→ 10 M * 0.005 L = C2 * 1.005 L
C2 = 0.04975 M the concentration of HCl after dilution
HCl → H+ + Cl-
0.04975 mol /L 0.04975 mol /L 0.04975 mol /L
pH = -log [H+] = -log [0.04975 M]= 1.3
So the pH of water had been dropped from 7 to 1.3 by addition of 5 mL
of 10 M HCl 40

41. Tolerance of a Buffer System:
Case#2
• Case #2
In comparison with Case#1.
For 1 L buffer solution of 0.364 M weak
acid [HA] and 0.636 M [A-] calculate the
initial and final pH after addition of 5 mL of
10 M HCl. Ka= 1.8 *10-5 (pKa= 4.757)
41

42. Tolerance of a Buffer System:
Case#2
• The initial pH for the buffer system can be
calculated using Henderson-Hasselbalch equation
pH= pKa + log ([A-]/[HA])
pH= 4.757 + log (0.636 M/ 0.364 M)
pH = 4.757 + 0.242 = 5
[H+] = 10-pH = 1.00 * 10-5
The [H+] can be calculated by another way
HA ⇌ H+ + A-
0.364 x 0.636
Ka= [H+][A-] /[HA]
[H+]= Ka * [HA] / [A-] = 1.8 *10-5 * 0.364 / 0.636
[H+]= 1.03 *10-5
pH = -log [H+]= -log [1.03 *10-5 ] = 5 42

43. Tolerance of a Buffer System:
Case#2
• For the addition of 5 mL of 10M HCl to 1 L of buffer,
the final volume of the solution will be 1.005 L.
HCl → H+ + Cl-
1 mol 1 mol 1 mol
Mol HCl = M * V = 10 M * 0.005 L = 0.05 mol = mol H+
HA ⇌ H+
+ A-
buffer 0.364 0.636
Added Acid 0.05
Reaction 0.364 + 0.05 x 0.636 -0.05
43

44. Tolerance of a Buffer System:
Case#2
The total volume of the solution after addition of 5 mL of 10 M HCl to 1 L of buffer =
1.005 L
Mol A- = 0.636 – 0.05 = 0.586
[A-] = 0.586 mol / 1.005 L = 0.583 M
Mol HA = 0.364 + 0.05 = 0.414
[HA] = 0.414 mol / 1.005 L = 0.412 M
pH= pKa + log ([A-]/[HA])
pH = 4.757 + log (0.583 / 0.412)= 4.90
Therefore, the pH of the buffer system has dropped by about 0.1 ( from 5.00 to 4.90)
In comparison with water, the buffer solution seems to be more resistance to the
addition of acid.
44

45. For the base

46. Fraction Dissociation
Fraction Dissociation = [A-]/total acid (all forms)
= [A-]/ ([HA] + [A-])
If [A-]= 0.0055
Total acid = [A-] + [HA] = F acid = 0.05
Fraction dissociation = 0.0055/0.05= 0.11 or 11%
From fraction dissociation determine Ka (if an acid is 1%
dissociated when the formal concentration is 0.1M, what is the
Ka?)
From pH at a given [ ] of weak acid determine the Ka (if the pH of
a 0.1M solution of acid is 2, what is the Ka of the acid?)
46

47. Buffers – Example
Self-excercise
• Calculate the pH of a buffer prepared by
dissolving 10.0 grams of NaOH in 500 mL of
a 0.800 M solution of acetic acid. Ignore
volume changes associated with the addition
of the solid NaOH.
Ans: 4.98

48. Buffers – Example
Self-excercise
• Calculate the mass of sodium acetate that
must be added to 500 mL of 0.600 M acetic
acid to produce a buffer with a pH of 4.50.
Ans: 13.5 g sodium acetate

49. Buffers – Example
Self excercise
• Calculate the pH of a buffer solution
prepared by mixing 250 mL of 0.500 M
NH3 and 250 mL of 0.400 M NH4Cl. Kb for
ammonia is 1.76 x 10-5 M.
• Ans: 4.66

50. Blood Buffering System
• Bicarbonate most significant buffer
• Formed from gaseous CO2
CO2 + H2O <-> H2CO3
H2CO3 <-> H+ + HCO3
-
• Normal value blood pH 7.4
• Deviations from normal pH value lead to
acidosis