The document discusses acid-base equilibria, including calculations for the pH of strong acids and strong bases, and how to find the pH of solutions resulting from mixing various acids and bases. It also covers the properties of salts derived from weak and strong acids/bases, buffer solutions, and polyprotic acids. Various calculations and examples illustrate the concepts of pH determination, buffer capacity, and the relationships between acidity constants.

1. 1
Acid-Base Equilibria

2. 2
pH calculations
1. Strong Acids and Strong Bases
Strong acids and strong bases are those
substances which are completely
dissociated in water and dissociation is
represented by one arrow pointing to
right. Examples of strong acids include
HCl, HBr, HI, HNO3, HClO4, and H2SO4
(only first proton). Examples of strong
bases include NaOH, KOH, Ca(OH)2, as
well as other metal hydroxides.

3. 3
Find the pH of a 0.1 M HCl solution.
HCl is a strong acid that completely
dissociates in water, therefore we have
HCl  H+ + Cl-
H2O D H+ + OH-
[H+]Solution = [H+]from HCl + [H+]from water
However, [H+]from water = 10-7 in absence of a
common ion, therefore it will be much less in
presence of HCl and can thus be neglected
as compared to 0.1 ( 0.1>>[H+]from water)
[H+]solution = [H+]HCl = 0.1M
pH = -log 0.1 = 1

4. 4
Find the pH of a 1x10-5 M HNO3 solution.
pH = - log 10-5 = 5

5. 5
Find the pH of a 10-10 M HCl solution.
HCl  H+ + Cl-
H2O D H+ + OH-
[H+]Solution = [H+]from HCl + [H+]from water
pH = 7

6. 6
Calculate the pH of the solution resulting from
mixing 50 mL of 0.1 M HCl with 50 mL of 0.2 M
NaOH.
When HCl is mixed with NaOH neutralization takes
place where they react in a 1:1 mole ratio.
Therefore, find mmol of each reagent to see if
there is an excess of either reagent
mmol HCl = 0.1 x 50 = 5 mmol
mmol NaOH = 0.2 x 50 = 10 mmol
mmol NaOH excess = 10 – 5 = 5 mmol
[OH-] = 5/100 = 0.05 M
pOH = 1.3 and pH = 14 – pOH = 14 – 1.3 = 12.7

7. 7
Find the pH of a solution prepared by mixing 2.0 mL of
a strong acid at pH 3.0 and 3.0 mL of a strong base
at pH 10.
Solution
First, find the concentration of the acid and the base
pH = 3.0 means [H+] = 10-3.0
pH = 10 means [H+] = 10-10 M or [OH-] = 10-4 M
Now find the number of mmol of each
mmol H+ = 10-3 x 2.0 = 2.0x10-3 mmol
mmol OH- = 10-4 x 3.0 = 3.0 x 10-4 mmol
mmol H+ excess = 2.0x10-3 – 3.0x10-4 = 1.7x10-3
[H+] = 1.7x10-3/5 = 3.4x10-4 M
pH = - log 3.4x10-4 = 3.5

8. 8
2. Salts of Strong Acids and Bases
The pH of the solution of salts of strong
acids or bases will remain constant (pH
= 7)

9. 9
3. Salts of Weak Acids and Bases
a. Salts derived from weak acids/bases and strong
bases/acids

10. 10
For the conjugate base of acetic acid (acetate)
we have
OAc- + H2O D HOAc + OH-
Kb = [HOAc][OH-]/[OAc-]
Let us multiply ka times kb we get
Ka kb = [H+][OH-] = kw , or
Ka kb = kw
Therefore, if we know the ka for the acid we can
get the equilibrium constant for its conjugate
base since we know kw. We can find ka for
the conjugate acid by the knowledge of the
equilibrium constant of the parent base.

11. 11
Find the pH of a 0.10 M solution of sodium
acetate. Ka = 1.75x10-5

12. 12
OAc- + H2O D HOAc + OH-
Kb = kw/ka
Kb = 10-14/1.75x10-5 = 5.7x10-10

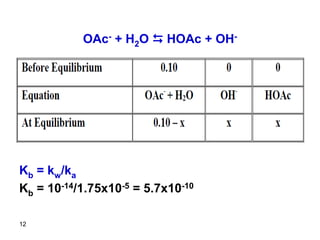
13. 13
Kb = [HOAc][OH-]/[OAc-]
Kb = x * x/(0.10 – x)
Kb is very small and we can fairly assume that
0.10>>x
5.7x10-10 = x2/0.1
x = 7.6 x 10-6
Relative error = (7.6x10-6/0.10) x100 = 7.6x10-3%
The assumption is valid.
[OH-] = 7.6x10-6 M
[H+] = 1.3x10-9 M = [OH-]water
pOH = 5.12
pH = 14 – 5.12 = 8.88

14. 14
therefore we can write
[H+]solution = [H+]ammonium
The first point is to write the equilibrium where
NH4
+ D H+ + NH3
Calculate the pH of a 0.25 M ammonium chloride solution. Kb =
1.75x10-5

15. 15
Ka = 10-14/1.75x10-5 = 5.7x10-10
Ka = [H+][NH3]/[NH4
+]
Ka = x * x / (0.25 – x)
Ka is very small. Assume 0.25 >> x
5.7*10-10 = x2/0.25
x = 1.2x10-5
Relative error = (1.2x10-5/0.25) x 100 = 4.8x10-3 %
The assumption is valid and the [H+] = 1.2x10-5 M
pH = 4.92

16. 16
b. Salts derived from weak acids/bases
and weak bases/acids
In this case, both ions are strong
conjugates that react with water and
may affect the pH of the solution.
For example, look at the calculation of pH
for a 0.1 M NH4CN (kb, NH3 = 1.8*10-5, ka,
HCN = 6*10-10)

17. 17
NH4
+ D H+ + NH3 ka = 5.7*10-10
CN- + H2O D HCN + OH- kb = 1.7*10-5
Comparing the equilibrium constants suggests
that the lower one is much larger than the
first. This suggests that:
1. The first equilibrium can be neglected.
2. The solution will be basic.
Since the solution is basic, water dissociation
can be assumed to be neglected as well,
due to common ion effect.

18. 18
It is therefore justified to assume that the only
important equilibrium is:
CN- + H2O D HCN + OH- kb = 1.7*10-5
0
0
Before equil
OH-
HCN
CN- + H2O
Equation
x
x
0.1 - x
After equil
Kb = [HCN][OH-]/[CN-]

19. 19
1.7*10-5 = x * x / (0.10 – x)
kb is very small that we can assume that
0.10>>x. We then have:
1.8*10-5 = x2 / 0.1
x = 1.3x10-3 M
Relative error = (1.3x10-3 /0.1) x 100 = 1.3%
The assumption is valid, therefore:
[OH-] = 1.3x10-3 M
pOH = 2.89
pH = 11.11

20. 20
Buffer Solutions
A buffer is a solution that resists changes in
pH upon addition of small quantities of acids
or bases. In other words, a buffer is a
solution that keeps its pH almost constant. A
buffer is a solution containing a weak acid
and its conjugate base or a weak base and
its conjugate acid. Below is an explanation of
how buffers work:
Let us look at a buffer formed from a weak acid
(like acetic acid) and its conjugate base (e.g.
sodium acetate); we have the following
equilibria:

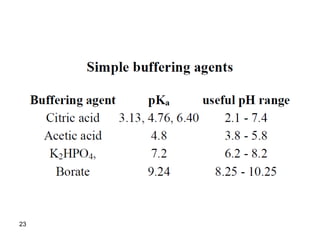
21. 21
Hasselbalch-Henderson Equation
In the acetic acid/acetate buffer described
above, we have:
Ka = [OAc-][H+]/[HOAc]
Pka = pH – log [OAc-]/[HOAc]
pH = pka + log [OAc-]/[HOAc]
The above equation is referred to as
Hasselbalch-Henderson equation.

22. 22
This equation can be useful to describe buffer
limits where the maximum pH limit for a
buffer is when the salt to acid ratio is 10 and
the minimum pH limit of the buffer is when
the acid to salt ratio is 10. Inserting these
values, one in a time, in the Hasselbalch
equation gives
pH = pka + 1
Therefore, the buffer acts well within two pH
units and the midpoint pH value is equal to
pka. One should first look at the pka or pkb to
choose the correct buffer system which can
be used within a specific pH range.

23. 23

24. 24
Calculate the pH of the buffer solution
prepared by mixing 10 mL 0.10 M HOAc (ka =
1.75x10-5) with 20 mL of 0.20 M sodium
acetate.
Solution
Let us first calculate the concentrations after
mixing (final concentrations of the acid and
its conjugate base)
mmol HOAc = 0.10 x 10 = 1.0 mmol
[HOAc] = 1.0/30
mmol OAc- = 0.20 x 20 = 4.0 mmol

25. 25
[OAc-] = 4.0/30
pH = 5.36 using Hasselbalch-Henderson Equation

26. 26
Calculate the pH of the solution resulting from
adding 25 mL of 0.10 M NaOH to 30 mL of
0.20 M acetic acid.
Solution
Let us find what happens when we mix the two
solutions. Definitely the hydroxide will react
with the acid to form acetate which also
results in a decrease in the acid
concentration.
mmol OH- = 0.10 x 25 = 2.5 mmol
mmol HOAc = 0.20 x 30 = 6.0 mmol

27. 27
Now the mmol base added will react in a 1:1 mole
ratio with the acid . Therefore we have
mmol HOAc left = 6.0 – 2.5 = 3.5 mmol
[HOAc] = 3.5/55 M
mmol OAc- formed = 2.5 mmol
[OAc-] = 2.5/55 M
pH = 4.61 using Hasselbalch-Henderson Equation

28. 28
4. Solutions of Polyprotic Acids
Polyprotic acids are weak acids, except sulfuric
acid where the dissociation of the first proton is
complete, which partially dissociate in water in
a multi step equilibria where hydrogen ions are
produced in each step.
Examples include carbonic, oxalic maleic,
phosphoric, etc.
A general simplification in the calculation of pH of
such acids is to compare ka1 and ka2 where
,usually ka1/ka2 is a large value (>102) and thus
equilibria other than the first dissociation step
can be ignored.

29. 29
Find the pH of a 0.10 M H3PO4 solution.
Solution
H3PO4 D H+ + H2PO4
- ka1 = 1.1 x 10-2
H2PO4
- D H+ + HPO4
2- ka2 = 7.5 x 10-8
HPO4
2- D H+ + PO4
3- ka3 = 4.8 x 10-13
Since ka1 >> ka2 (ka1/ka2 > 102) the amount of H+
from the second and consecutive equilibria
is negligible if compared to that coming from
the first equilibrium.

30. 30
Therefore, we can say that we only have:
H3PO4 D H+ + H2PO4
- ka1 = 1.1 x 10-2

31. 31
Ka1 = x * x/(0.10 – x)
Assume 0.10>>x since ka1 is small (!!!)
1.1*10-2 = x2/0.10
x = 0.033
Relative error = (0.033/0.10) x 100 = 33%
The assumption is invalid and thus we have to
use the quadratic equation. If we solve the
quadratic equation we get:
X = 0.028
Therefore, [H+] = 0.028 M
pH = 1.55

32. 32
Find the pH of a 0.10 M H2CO3 solution.
Ka1 = 4.3x10-7, ka2 = 4.8x10-11
Solution
We have the following equilibria
H2CO3 D H+ + HCO3
- ka1 = 4.3 x 10-7
HCO3
- D H+ + CO3
2- ka2 = 4.8 x 10-11
Since ka1 is much greater than ka2, we can
neglect the H+ from the second step

33. 33
H2CO3 D H+ + HCO3
- ka1 = 4.3 x 10-7
Ka1 = x * x/(0.10 – x)
Assume 0.10>>x since ka1 is small
4.3*10-7= x2/0.10
x = 2.1x10-4
Relative error = (2.1x10-4/0.10) x 100 = 0.21%
The assumption is valid and [H+] = 2.1x10-4 M
pH = 3.68

34. 34
Buffer Calculations for Polyprotic Acids
A polyprotic acid can form buffer solutions in
presence of its conjugate base. For example,
phosphoric acid can form a buffer when
combined with its conjugate base (dihydrogen
phosphate).
H3PO4 D H+ + H2PO4
- ka1 = 1.1 x 10-2
This buffer operates in the range:
pH = pka + 1 = 0.96 – 2.96

35. 35
Also, another buffer which is commonly used
is the dihydrogen phosphate/hydrogen
phosphate buffer.
H2PO4
- D H+ + HPO4
2- ka2 = 7.5 x 10-8
This buffer operates in the range from 6.1 to
8.1
A third buffer can be prepared by mixing
hydrogen phosphate with orthophosphate
as the following equilibrium suggests:
HPO4
2- D H+ + PO4
3- ka3 = 4.8 x 10-13
This buffer system operates in the pH range
from 11.3 to 13.3

36. 36
The same can be said about carbonic acid/bicarbonate
where
H2CO3 D H+ + HCO3
- ka1 = 4.3 x 10-7
This buffer operates in the pH range from 5.4 to 7.4;
while a more familiar buffer is composed of
carbonate and bicarbonate according to the
equilibrium:
HCO3
- D H+ + CO3
2- ka2 = 4.8 x 10-11
The pH range of the buffer is 9.3 to 11.3.
Polyprotic acids and their salts are handy materials
which can be used to prepare buffer solutions of
desired pH working ranges. This is true due to the
wide variety of their acid dissociation constants.

37. 37
Find the ratio of [H2PO4
-]/[HPO4
2-] if the pH of
the solution containing a mixture of both
substances is 7.4. ka2 = 7.5x10-8
Solution
The equilibrium equation combining the two
species is:
H2PO4
- D H+ + HPO4
2- ka2 = 7.5 x 10-8
Ka2 = [H+][HPO4
2-]/[H2PO4
-]
[H+] = 10-7.4 = 4x10-8 M
7.5x10-8 = 4x10-8 [HPO4
2-]/[H2PO4
-]
[HPO4
2-]/[H2PO4
-] = 1.9

38. Buffers with Specific Ionic
Strength
How many mL of 12.0 M acetic acid and how many grams of sodium
acetate (FW = 82 g/mol) are needed to prepare a 500 mL buffer at pH
5.0, and having an ionic strength of 0.2. ka = 1.8*10-5
We need to find the concentration of the salt:
m = ½ S CiZi
2
0.2 = ½ (CNa
+ * 12 + COAc
- * 12)
CNa
+ = COAc
-
0.2 = ½ (2CNa
+ )
CNa
+ = COAc
- = 0.2 M = CNaOAc
mmol NaOAC = 0.2*500 = 100
mg NaOAc = 100*82 = 8200 mg or 8.2 g
38

39. HOAc D H+ + OAc-
We can now find the concentration of the acid
where:
1.8*10-5 = 10-5*0.2/[HOAc]
[HOAc] = 0.2/1.8 = 0.11 M
mmol HOAc = 0.11*500 = 55.6
12.0*VHOAc = 55.6
VHOAc = 4.6 mL
39

40. 40
5. pH Calculations for Salts of Polyprotic Acids
Two types of salts exist for polyprotic acids.
These include:
1. Unprotonated salts
These are salts which are proton free which
means they are not associated with any
protons. Examples are: Na3PO4 and Na2CO3.
Calculation of pH for solutions of such salts
is straightforward and follows the same
scheme described earlier for salts of
monoprotic acids.

41. 41
Find the pH of a 0.10 M Na3PO4 solution.
Solution
We have the following equilibrium in water
PO4
3- + H2O D HPO4
2- + OH-
The equilibrium constant which corresponds to
this equilibrium is kb where:
Kb = kw/ka3

42. 42
We used ka3 since it is the equilibrium constant
describing relation between PO4
3- and HPO4
2.
However, in any equilibrium involving salts
look at the highest charge on any anion to
find which ka to use.
Kb = 10-14/4.8x10-13
Kb = 0.020

43. 43
Kb = x * x/0.10 – x
Assume 0.10 >> x
0.02 = x2/0.10
x = 0.045
Relative error = (0.045/0.10) x 100 = 45%
Therefore, assumption is invalid and we have
to use the quadratic equation. If we solve the
quadratic equation we get:
X = 0.036
Therefore, [OH-] = 0.036 M
pOH = 1.44 and pH = 14 – 1.44 = 12.56

44. 44
2. Protonated Salts
These are usually amphoteric salts which
react as acids and bases. For example,
NaH2PO4 in water would show the following
equilibria:
H2PO4
- D H+ + HPO4
2-
H2PO4
- + H2O D OH- + H3PO4
H2O D H+ + OH-
[H+]solution = [H+]H2PO4
- + [H+]H2O – [OH-]H2PO4
-
[H+]solution = [HPO4
2-] + [OH-] – [H3PO4]

45. 45
Now make all terms as functions in either H+ or H2PO4
-, then we have:
[H+] = {ka2[H2PO4
-]/[H+]} + kw/[H+] – {[H2PO4
-][H+]/ka1}
Rearrangement gives
[H+] = {(ka1kw + ka1ka2[H2PO4
-])/(ka1 + [H2PO4
-]}1/2
At high salt concentration and low ka1 this relation may be approximated to:
[H+] = {ka1ka2}1/2
Where; the pH will be independent on salt
concentration but only on the equilibrium
constants.

46. 46
Protonated Salts with multiple charges
HPO4
2- is a protonated salt which behaves as an
amphoteric substance where the following equilibria
takes place:
HPO4
2- D H+ + PO4
3-
HPO4
2- + H2O D H2PO4
- + OH-
H2O D H+ + OH-
[H+] = [H+]HPO4
- + [H+]water – [OH-]HPO4
-
[H+] = [PO4
3-] + [OH-] – [H2PO4
-]
[H+] = ka3 [HPO4
2-]/[H+] + kw/[H+] – [H+][HPO4
2-]/ka2
Rearrangement of this relation gives
[H+] = {(ka2kw + ka2ka3 [HPO4
2-])/(ka2 + [HPO4
2-])}1/2
Approximation, if valid, gives:
[H+] = (ka2ka3)1/2

47. 47
Find the pH of a 0.10 M NaHCO3 solution. ka1 = 4.3
x 10-7, ka2 = 4.8 x 10-1
[H+] = {ka1ka2}1/2
[H+] = {4.3x10-7 * 4.8x10-11}1/2 = 4.5x10-9 M
pH is 8.34
This is since the salt concentration is high
enough. Now look at the following example
and compare:

48. 48
Find the pH of a 10-3 M NaHCO3 solution. ka1 =
4.3 x 10-7, ka2 = 4.8 x 10-1
Substitution in the relation [H+] = {ka1ka2}1/2 will
give pH 8.34 not accurate
Accurate
pH = 8.10

49. 49
Find the pH of a 0.20 M Na2HPO4 solution. Ka1 =
1.1x10-2, ka2 = 7.5x10-8, ka3 = 4.8x10-13.
Using the approximated expression we get:
[H+] = (7.5x10-8 * 4.8x10-13)1/2 = 1.9x10-10 M
pH = 9.72

50. 50
6. pH Calculations for Mixtures of Acids
The key to solving such type of problems
is to consider the equilibrium of the
weak acid and consider the strong acid
as 100% dissociated as a common ion.

51. 51
Find the pH of a solution containing 0.10 M HCl
and 0.10 M HNO3.
Solution
[H+] = [H+]HCl + [H+]HNO3
Both are strong acids which are 100%
dissociated. Therefore, we have
[H+] = 0.10 + 0.10 = 0.2
pH = 0.70

52. 52
Example
Find the pH of a solution containing 0.10 M HCl
and 0.10 M HOAc. ka = 1.8x10-5
Solution
HOAc D H+ + OAc-

53. 53
Ka = (0.10 + x) x/(0.10 – x)
Assume 0.1 >> x since ka is small
1.8x10-5 = 0.10 x/0.10
x = 1.8x10-5
Relative error = (1.8x10-5/0.10) x100 = 1.8x10-2%
Therefore [H+] = 0.10 + 1.8x10-5 = 0.10
pH is 1
It is clear that all H+ comes from the strong
acid since dissociation of the weak acid is
limited and in presence of strong acid the
dissociation of the weak acid is further
suppressed.

54. 54
Find the pH of a solution containing 0.10 M H3PO4 (ka1 =
1.1x10-2, ka2 = 7.5x10-8, ka3 = 4.8x10-13) and 0.10 M
HOAc (ka = 1.8x10-5).
Solution
It is clear for the phosphoric acid that we can disregard
the second and third equilibria since ka1>>> ka2.
Therefore we treat the problem as if we have the
following two equilibria:
H3PO4 D H+ + H2PO4
-
HOAc D H+ + OAc-

55. 55
Now compare the ka values for both equilibria:
Ka1/ka = 1.1x10-2/1.8x10-5 = 6.1x102
Therefore the first equilibrium is about 600 times better
than the second. For the moment, let us neglect H+
from the second equilibrium as compared to the
first.
Solution for the H+ is thus simple
H3PO4 D H2PO4
- + H+

56. 56
Ka = x * x/(0.10 – x)
Assume 0.1 >> x since ka is small (!!!)
1.1x10-2 = x2 /0.10
x = 0.033
Relative error = (0.033/0.10) x100 = 33 %
The assumption is therefore invalid and we
have to solve the quadratic equation. Result
will be
X = 0.028 pH is 1.55

57. Find the pH of a mixture containing 0.10 M
H3PO4 and 0.1 M H2CO3 solution.
H3PO4 D H+ + H2PO4
- ka1 = 1.1 x 10-2
H2PO4
- D H+ + HPO4
2- ka2 = 7.5 x 10-8
HPO4
2- D H+ + PO4
3- ka3 = 4.8 x 10-13
Ka1/ka2 ~ 106, therefore, only first equilibrium is
important
H2CO3 D H+ + HCO3
- ka1 = 4.3 x 10-7
HCO3
- D H+ + CO3
2- ka2 = 4.8 x 10-11
Ka1/ka2 ~ 104, therefore, only first equilibrium is
important

58. H3PO4 D H+ + H2PO4
- ka1 = 1.1 x 10-2
H2CO3 D H+ + HCO3
- ka1 = 4.3 x 10-7
As before pH is 1.55