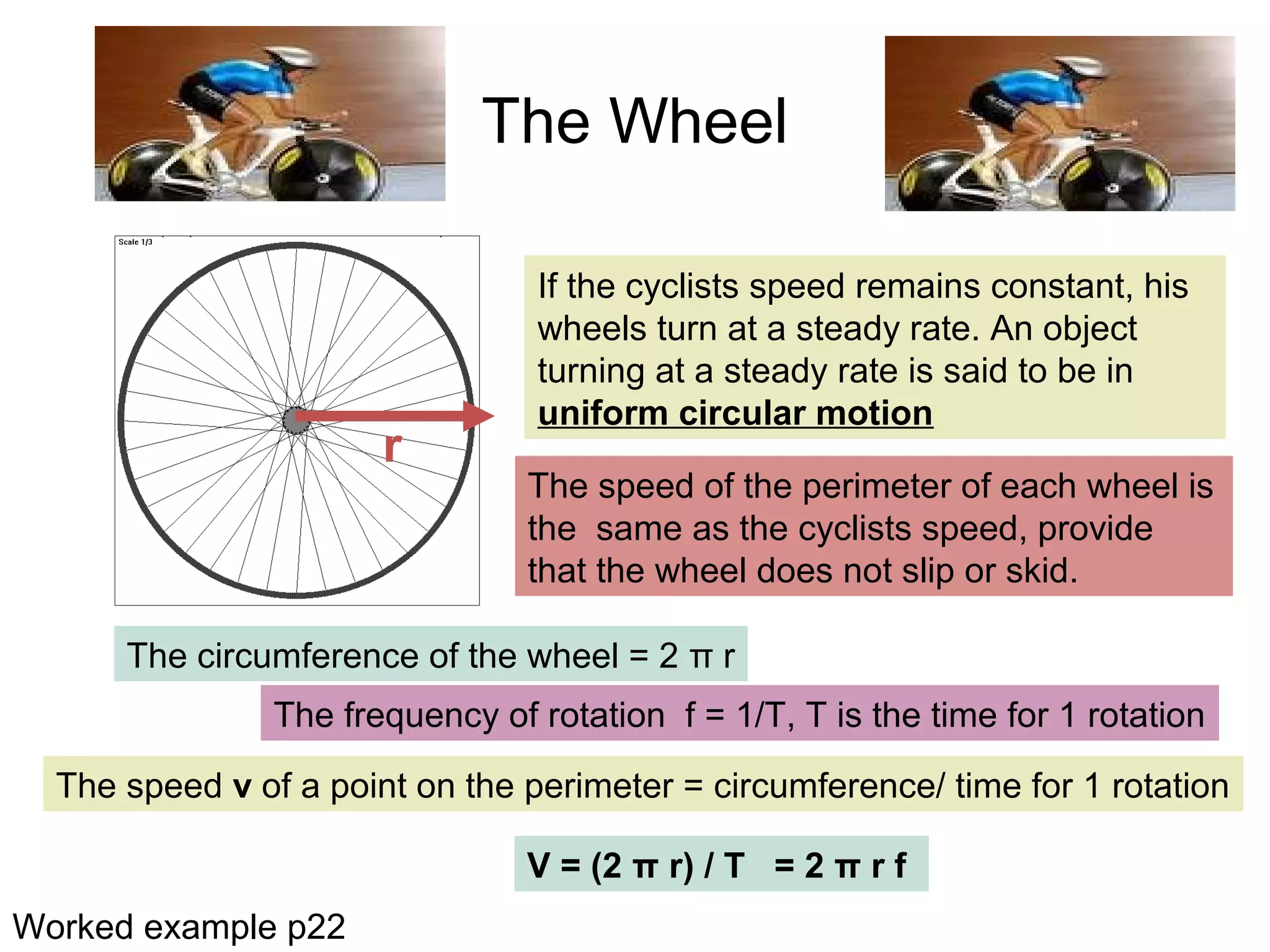
The document discusses the forces experienced when an object moves in a circular path, particularly focusing on why cars skid when cornering too quickly. It explains concepts such as uniform circular motion, angular displacement, and angular speed, providing examples like hammer throwing, spinning fairground rides, and satellites in orbit. Additionally, it includes calculations for angular speed and displacement, exemplified by a big wheel with a specific diameter and rotation time.

1. Moving in Circles
What forces are
on you when
you go around
a corner?

2. Task
• Try and explain why a car skids when it goes
around a corner too quickly.

3. Learning objectives
• How can we recognise uniform motion in a
circle?
• What do we need to measure to find the
speed of an object moving in uniform
circular motion?
• What is meant by angular displacement
and angular speed?

4. Objects which move in a circular path
any suggestions?
The hammer swung by a hammer thrower
Clothes being dried in a spin drier
Chemicals being separated in a centrifuge
Cornering in a car or on a bike
A stone being whirled round on a string
A plane looping the loop
A DVD, CD or record spinning on its turntable
Satellites moving in orbits around the Earth
A planet orbiting the Sun (almost circular orbit for many)
Many fairground rides
An electron in orbit about a nucleus

5. The Wheel
The speed of the perimeter of each wheel is
the same as the cyclists speed, provide
that the wheel does not slip or skid.
r
If the cyclists speed remains constant, his
wheels turn at a steady rate. An object
turning at a steady rate is said to be in
uniform circular motion
The circumference of the wheel = 2 π r
The frequency of rotation f = 1/T, T is the time for 1 rotation
The speed v of a point on the perimeter = circumference/ time for 1 rotation
V = (2 π r) / T = 2 π r f
Worked example p22

6. Angular displacement
The big wheel has a diameter of 130m and a full
rotation takes 30 minutes (1800 seconds)
3600
/ 1800 = 0.20
per second (2π radians)
20
in 10 seconds
200
in 100 seconds (π/18 radians)
900
in 450 seconds (π/2 radians)
The wheel will turn through an angle of (2 π/T) radians per second
T is the time for one complete rotation
The angular displacement (in radians) of the object in time t is therefore
= 2 π t
T
= 2 π f t
The angular speed (w) is defined as the angular displacement / time
w = 2 π f w is measured in radians per second (rad s-1
)

7. Angular displacement
The big wheel has a diameter of 130m and a full
rotation takes 30 minutes (1800 seconds)
3600
/ 1800 = 0.20
per second (2π radians)
20
in 10 seconds
200
in 100 seconds (π/18 radians)
900
in 450 seconds (π/2 radians)
The wheel will turn through an angle of (2 π/T) radians per second
T is the time for one complete rotation
The angular displacement (in radians) of the object in time t is therefore
= 2 π t
T
= 2 π f t
The angular speed (w) is defined as the angular displacement / time
w = 2 π f w is measured in radians per second (rad s-1
)