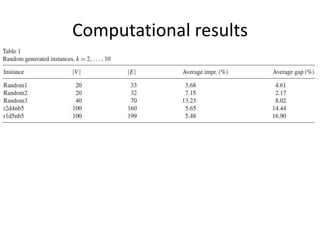
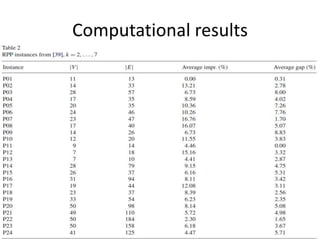
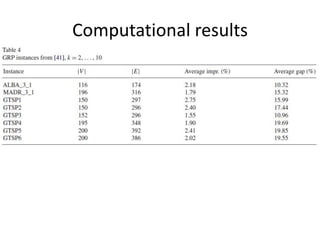
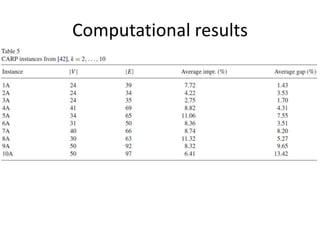
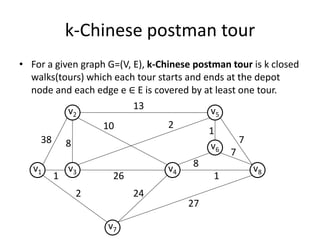
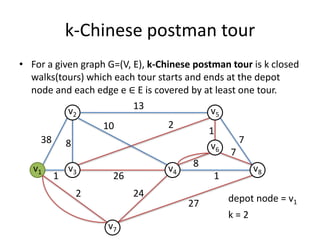
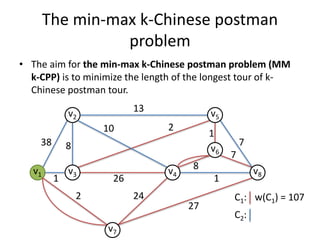
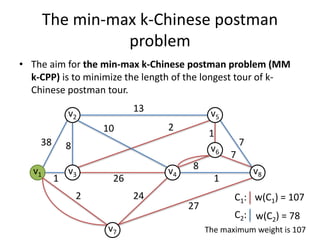
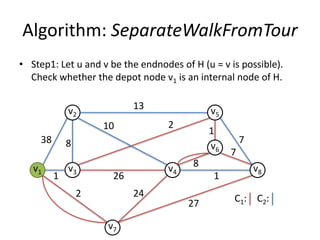
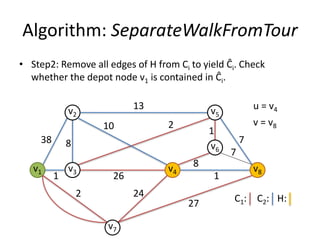
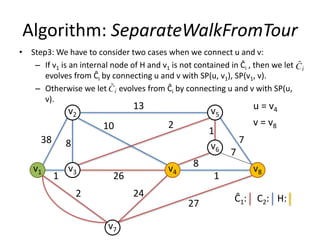
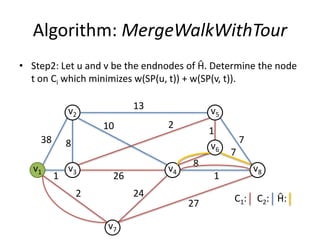
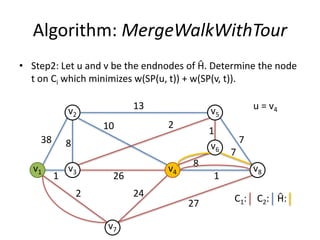
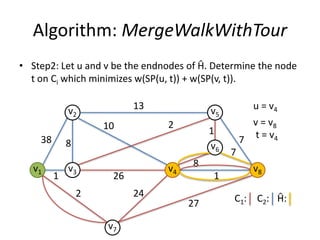
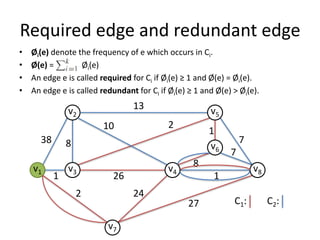
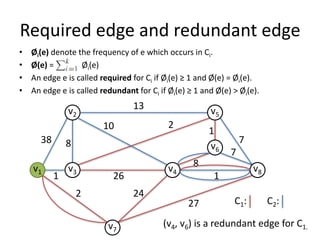
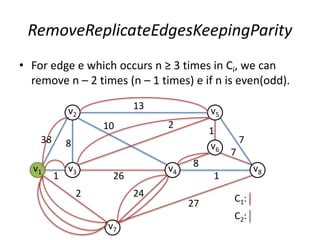
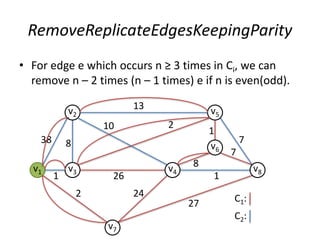
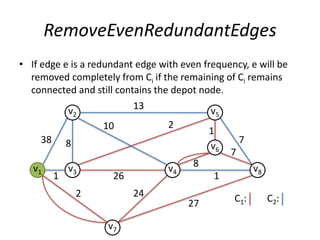
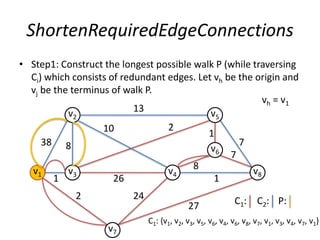
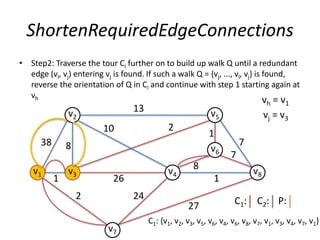
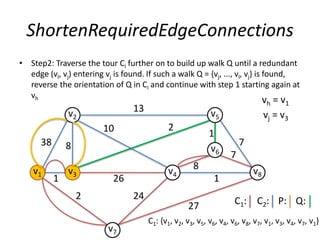
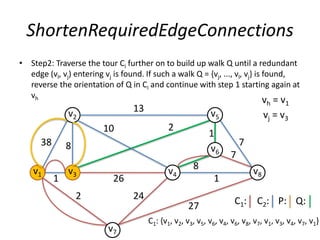
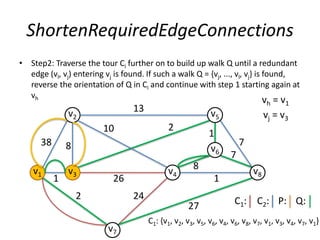
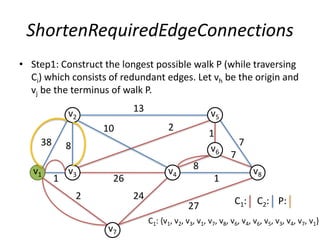
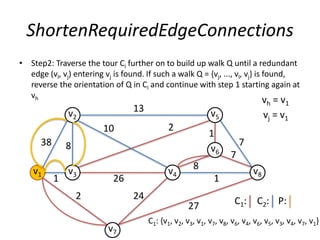
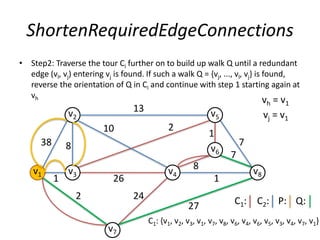
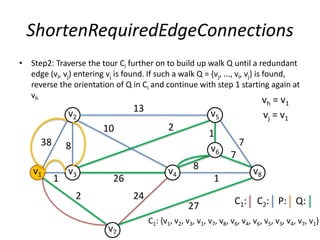
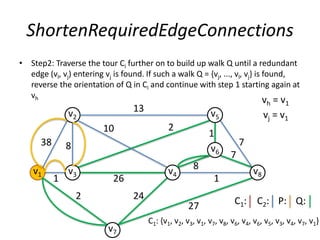
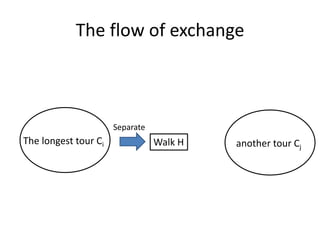
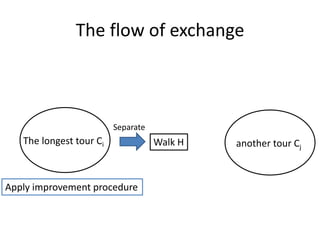
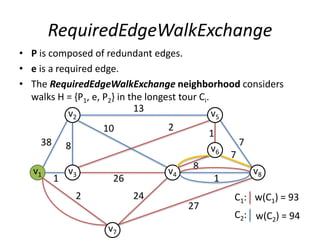
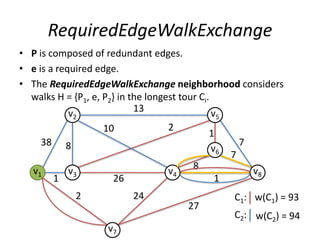
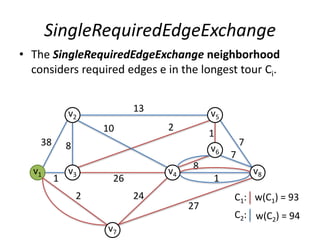
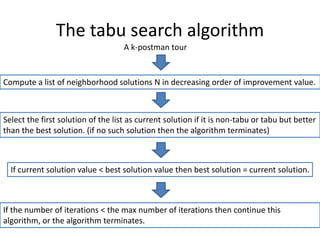
The document describes the min-max k-Chinese postman problem and algorithms for solving it. The min-max k-Chinese postman problem aims to minimize the length of the longest tour in a k-Chinese postman tour (which consists of k closed walks that each start/end at a depot node and together cover all edges). The document outlines algorithms for merging and separating edges between tours, and a tabu search algorithm is used to iteratively improve tours. Computational results are also presented.












































































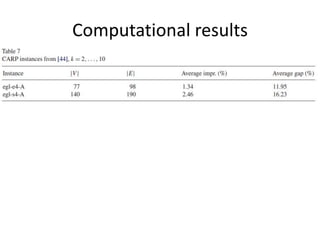
![Computational results
• Two improvement index
– Let x be the value of the best heuristic solution from
[2]
– Let y be the best solution value obtained by the tabu
search algorithm for all possible configurations of
neighborhood structures and improvement
procedures.
– Let z be the best lower bound obtained by the lower
bounds SPT-LB and CPP/k-LB presented in [2].
– Average impr.(%) = (x - y) * 100 / x
– Average gap(%) = (y - z) * 100 / y](https://image.slidesharecdn.com/atabusearchalgorithmforthemin-maxk-chinesepostmanproblem-150919152741-lva1-app6892/85/A-tabu-search-algorithm-for-the-min-max-k-chinese-postman-problem-112-320.jpg)