This document summarizes a research paper that proposes a new approach for two-level logic synthesis called constrained depth-first search. It generates all prime implicants of a Boolean function efficiently using cube absorption and a position cube notation representation. It then formulates the problem of finding an optimal sum-of-products cover as a combinatorial optimization problem. The key contribution is a constrained depth-first search of a virtual prime implicant decision tree that finds the minimum cover. Numerical results on benchmark functions show it produces results as good or better than state-of-the-art logic synthesis tools, often finding the greedy solution is already optimal or near-optimal.

1. International INTERNATIONAL Journal of Computer JOURNAL Engineering OF and COMPUTER Technology (IJCET), ENGINEERING ISSN 0976-6367(Print),
&
ISSN 0976 - 6375(Online), Volume 5, Issue 11, November (2014), pp. 23-31 © IAEME
TECHNOLOGY (IJCET)
ISSN 0976 – 6367(Print)
ISSN 0976 – 6375(Online)
Volume 5, Issue 11, November (2014), pp. 23-31
© IAEME: www.iaeme.com/IJCET.asp
Journal Impact Factor (2014): 8.5328 (Calculated by GISI)
www.jifactor.com
IJCET
© I A E M E
A MINIMIZATION APPROACH FOR TWO LEVEL LOGIC
SYNTHESIS USING CONSTRAINED DEPTH-FIRST
SEARCH
Vikul Gupta
Oregon Episcopal School, Portland, Oregon, USA
23
ABSTRACT
Two-level optimization of Boolean logic circuits, expressed as Sum-of-Products (SOP), is an
important task in VLSI design. It is well known that an optimal SOP representation for minimizing
gate input count is a cover of prime implicants. Determination of an optimal SOP involves two steps:
first step is generating all prime implicants of the Boolean function, and the second step is finding an
optimal cover from the set of all prime implicants. A cube absorption method for generating all
prime implicants is significantly more efficient than the tabular Quine-McCluskey method, when
implemented using the position cube notation (PCN) to represent product cubes, and efficient bit
manipulations to implement the cube operations. The main contribution of this paper is a constrained
depth-first search (dfs) of the prime implicant decision tree to find the optimal cover, which is posed
as a combinational optimization problem. A virtual representation of the decision tree is arranged
such that the first path explored in a depth first search manner corresponds to the greedy solution to
this problem, and further paths are explored only if they improve the current minimum solution. The
exponential explosion of the search space is tamed by using this efficient search approach, and
terminating the search at suitably large thresholds. Numerical results of synthesizing benchmark
PLA functions show that for a vast majority of the tests, the results produced by constrained dfs
approach are better or as good as those produced by state-of-the-art logic synthesis. Another
interesting observation is that the greedy solution is often a minimum solution, and even in the other
cases, it was not improved significantly by the dfs search.
Keywords: Two-Level Logic Synthesis, Minimum Prime Implicant Covers, Constrained Depth First
Search, PCN Implementation of Product Cubes, VLSI Design.

2. International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print),
ISSN 0976 - 6375(Online), Volume 5, Issue 11, November (2014), pp. 23-31 © IAEME
24
I. INTRODUCTION
Digital electronics has revolutionized our world in the last 50 years. Starting with arithmetic
computations on behemoth computers, today digital systems are pervasive everywhere, in smart
phones, notepads, audio and video systems, medical devices, automotive systems, and of course, in
global communication systems and back offices of all corporations. This has been enabled by the
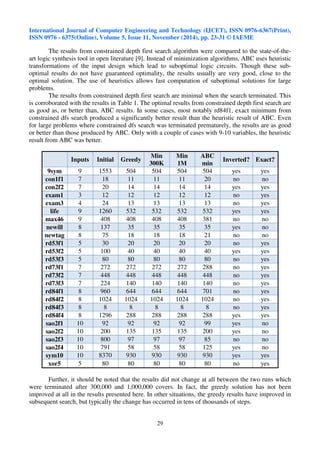
exponential increase in the number of transistors that can be integrated on a silicon wafer since the
1960s, with state of the art chips today containing upwards of 5 billion transistors [1]. With such
powerful implementation technologies available, increasingly innovative and complex systems are
being designed and implemented in semiconductor technology. Logic design of such systems has
been feasible with electronic design automation (EDA) systems because it is impossible to design
such complex systems manually. As a result, automated synthesis of optimal logic design from high
level description has received considerable research attention over the years. This paper describes a
new logic synthesis approach for minimization of two level logic circuits.
In the high-level design of digital systems, combinational logic is expressed as Boolean
expressions in some suitable format, typically expressions in a hardware description language such
as SystemVerilog. Logic synthesis is the process of transforming these expressions to a network of
logic gates which can be implemented with the desired semiconductor technology. Two-level
synthesis converts the logic functions to a sum-of-products (SOP) form which is technology
independent. Multiple two-level networks of AND and OR gates representing a logic function can be
generated. The goal is to find the network which uses the minimum number of gates. Even though
this was one of the early problems analyzed in logic synthesis, it is still a significant problem. Circuit
realizations with technologies like programming logic arrays (PLAs) benefit directly from optimal
SOP representations. Further, a common approach to logic synthesis is to first perform technology
independent optimization of logic in a presentation like SOP, and then map this technology
independent solution to the appropriate semiconductor technology.
It is well known that a minimizing sum-of-products representation with respect to number of
gates is a cover of prime implicants[2, 3]. Determining the optimal SOP representation involves first
determining all prime implicants of the logic function, and then selecting a set of prime implicants
that cover the function with minimum number of gates. Karnaugh maps provide a manual, textbook
approach for determining the prime implicants of a Boolean function. Then, ad hoc heuristics can be
employed to select a low cost SOP implementation. This approach works for 5 or 6 variables,
beyond that it is not humanly possible to manage all the possibilities. A tabulation procedure, known
as the Quine-McCluskey method of reduction[3], can be used to determine all prime implicants
given the on-set or minterms of a logic function. This systematic procedure could be programmed on
a computer to automatically generate prime implicants of functions with larger number of variables.
Once all prime implicants have been obtained, prime covers are generated using the prime implicant
charts. The Petrick-method provides another interesting approach for generating all the covers from
the set of prime implicants. The cost of each of these covers can be obtained in terms of the number
of gates used, and the minimum cover is selected as the exact minimum solution. The fundamental
problem is the exponential growth in the search space as the problem size in terms of the number of
input variables increases. Heuristic approaches described in [6] are used to get around this problem
of exponential increase in search space and compute resources. These approaches do not guarantee
the exact minimum solutions but lead to sub-optimal solutions which are quite efficient in practice.
This paper alleviates the limitations of the current exact minimization approaches with a new
search scheme that allows exact minimum of larger problems. Efficient software implementation of
the cube absorption approach [3, 4] is used generating all prime implicants of a logic function. New
algorithms for cube operations in PCN representation are presented. The main contribution of this
paper is a constrained depth first search approach to determine exact minimum cost covers of prime

3. International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print),
ISSN 0976 - 6375(Online), Volume 5, Issue 11, November (2014), pp. 23-31 © IAEME
implicants. A decision tree of prime implicants is arranged in a manner that enables rapid search of
minimum solutions; in particular, the greedy solution is the first solution obtained in this search.
Further, the dfs search is constrained to traverse only those paths that could potentially improve the
current minimum cost. Details of this method are described in Section 4 of this paper.
This paper is organized as follows: Section 2 describes the necessary background ideas
needed in this work. Cube operations and their efficient implementation are described in Section 3.
The main contribution of this work, the cost-constrained depth first search is described in detail
Section 4. Numerical results are presented in Section 5, comparing this approach with state-of-the-art
logic synthesis tools, to quantify the benefits of this approach. Finally, Section 6 discusses
conclusions of this work and possible extensions for future.
25
II. BACKGROUND
Minimal two level logic synthesis, in terms of sum-of-products, of Boolean logic functions, is
discussed in this paper. This section reviews relevant concepts for this discussion. Note that,
mathematically, Boolean algebra characterizes a class of abstract algebras. However, in this paper,
the commonly understood meaning of Boolean algebra as the binary Boolean algebra or switching
algebra is used.
The Boolean values are denoted as and . Thus, the set of Boolean values is . A
Boolean variable takes one of these Boolean values, . The domain of n input variables

4. is
. Thus,
, is a Boolean function of n input variables. The on-set
of a function, , is defined as
. Similarly, the off-setis
. Note that since , 0 and 1 are the only possible values of , thus, the on-set,
, completely specifies the Boolean function.
Boolean values of variables can be viewed as a string of binary values, which can be
interpreted as an unsigned decimal number. For example, suppose a 3-input variable, , has
the values

5. . These values can be viewed as the binary string 110 which may be
interpreted as the number 6. With this interpretation, all possible values of n variables can be
represented as integers between 0 and
. In particular, the on-set of a Boolean function can be
specified as a subset of integers in this range. For example,

6. , is equivalently defined
by !#.
A literal is an input variable in true or complemented form, that is, $ or $
. A product term is
a product
of one or more literals. If all the literals are present in a product term, it is called a
minterm. The on-set of a minterm is one integer. For example, on-set of

7. , is {5}. Similarly,
the on-set of product term 1, 3}.
A product term, %, is an implicant of a Boolean function, , if %, or equivalently,
% ' . An implicant is a prime implicant of if there is no other product implicant of which
implies this implicant as well. A set of prime implicants, ( %

8. %
%), is said to cover the
function, , if the union of on-sets of these prime implicants is equal to the on-set of the function,
( *%$
. A set of prime implicants is irredundant if no prime implicant can be removed
from the set without changing its on-set. As shown in [2], a minimal sum-of-products representation
of a Boolean function must be an irredundant set of prime implicants. Thus, using the number of
gates as the cost, a minimal two-level implementation is an irredundant set of prime implicants.
Minimal two-level representations of Boolean functions are obtained in two steps. First,
generate all possible prime implicants of the Boolean function, and, second, search for lowest cost
irredundant set of prime implicants that covers the function, from all possible sets. The textbook
approach to generate all prime implicants of a function is the Quine-McClusky tabulation approach
[2, 3]. However, it is noted that a cube absorption approach [4, 5], with efficient algorithmic

9. International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print),
ISSN 0976 - 6375(Online), Volume 5, Issue 11, November (2014), pp. 23-31 © IAEME
implementation described in the next section, results in significantly better performance on large
problems. The second aspect of minimal two-level synthesis is searching for the lowest cost
irredundant set of prime implicants covering the Boolean function [6]. The prime-implicant chart and
the Petrick method are common approaches for exhaustively enumerating all possible covers. These
exhaustive approaches are limited to small problems, because of exponential growth as the number
of input variables increases. Combinational optimization approach to this problem leads to efficient
solutions. This paper presents a greedy algorithm [7], which can be extended to constrained depth
first search for an exact minimum.
III. PRIME IMPLICANTS WITH CUBE ABSORBTION
Computational Boolean reasoning can be performed very efficiently with vertices of a unit
cube in -dimensional space [4]. Product terms with Boolean variables can be represented as
vertices of an -d unit cube. For example, a 3 variable minterm