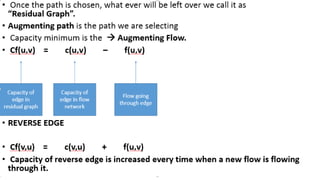
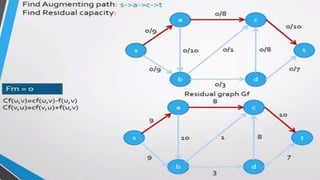
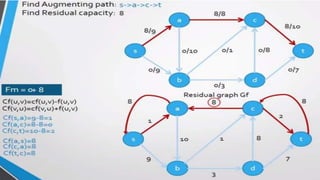
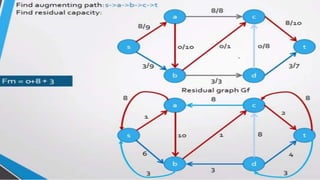
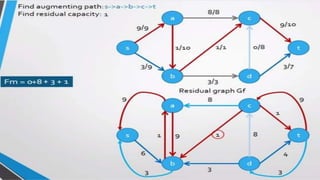
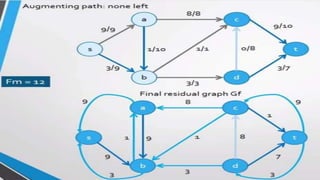
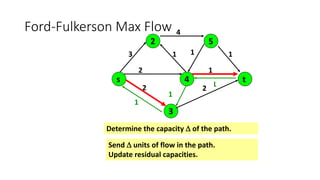
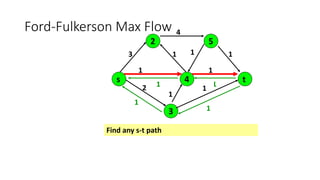
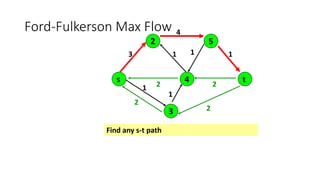
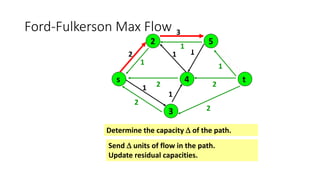
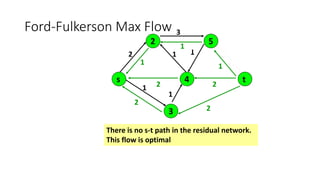
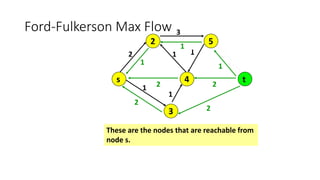
- The document discusses max flow and flow networks. It describes a scenario where an oil company owner needs to maximize the amount of oil sent from a source to a destination city using a network of pipelines. - A flow network is represented as a graph with nodes (cities) and edges (pipelines) that have capacity constraints. The Ford-Fulkerson algorithm is used to find the maximum flow from the source to the destination. - It works by finding augmenting paths in the residual network to incrementally increase the flow until no more paths exist, giving the optimal maximum flow through the network.

1. Max Flow and Flow Network
• Ur a owner of oil company, & your work is you have a source and destination and you
have to send the oil from source to the destination city.
• Network of pipeline has some capacity. (Edges are pipelines with capacity in gallons per
day)
• Ask manager, please tell in which of the pipeline I have to put how many gallons of oil
so that I can pump maximum max amount of oil to the destination.
• Flow F
f ( u,v)  Flow going out from u to v
C(u,v)  Max capacity it can carry.
Oil flowing/ Oil capacity.

11. Update the maximum flow, and capacities on the edges

12. Ford-Fulkerson Max Flow 4
1
1
2
2
1
2
3
3
1
s
2
4
5
3
t
This is the original network, and
the original residual network.

13. 4
1
1
2
2
1
2
3
3
1
Ford-Fulkerson Max Flow
Find any s-t path in G(x)
s
2
4
5
3
t

14. 4
1
1
2
1
3
Ford-Fulkerson Max Flow
Determine the capacity D of the path.
Send D units of flow in the path.
Update residual capacities.
1
1
1
2
1
2
3
2
1
s
2
4
5
3
t

15. 4
1
1
2
1
3
Ford-Fulkerson Max Flow
Find any s-t path
1
1
1
2
1
2
3
2
1
s
2
4
5
3
t

16. 4
2
1
1
1
1
2
2
1
1
1
1
3
Ford-Fulkerson Max Flow
1
1
1
1
3
2
1
s
2
4
5
3
t
Determine the capacity D of the path.
Send D units of flow in the path.
Update residual capacities.

17. 4
2
1
1
1
1
2
2
1
1
1
1
3
Ford-Fulkerson Max Flow
1
1
1
1
3
2
1
s
2
4
5
3
t
Find any s-t path

18. 1
1 1
1
1
4
1
2
1
1
2
1
1
3
Ford-Fulkerson Max Flow
1
1
3
2
1
s
2
4
5
3
t
Determine the capacity D of the path.
Send D units of flow in the path.
Update residual capacities.

19. 1
1 1
1
1
4
1
2
1
1
2
2
1
1
3
Ford-Fulkerson Max Flow
1
1
3
2
1
s
2
4
5
3
t
Find any s-t path

20. 1
1
1
2
1 1
1
1
4
2
2
1
1
2
2
1
Ford-Fulkerson Max Flow
1
1
3
1
1
s
2
4
5
3
t
Determine the capacity D of the path.
Send D units of flow in the path.
Update residual capacities.
2

21. 1
1
2
1 1
1
1
4
2
2
1
1
2
2
1
Ford-Fulkerson Max Flow
1
1
3
1
1
s
2
4
5
3
t
Find any s-t path
2

22. 1
1
1
1
1
4
1
3
1
1
2
1 1
3
2
2
1
2
1
Ford-Fulkerson Max Flow
2
1
s
2
4
5
3
t
2
Determine the capacity D of the path.
Send D units of flow in the path.
Update residual capacities.

23. 1
1
1
1
1
4
1
3
1
1
2
1 1
3
2
2
1
2
1
Ford-Fulkerson Max Flow
2
1
s
2
4
5
3
t
2
There is no s-t path in the residual network.
This flow is optimal

24. 1
1
1
1
1
4
1
3
1
1
2
1 1
3
2
2
1
2
1
Ford-Fulkerson Max Flow
2
1
s
2
4
5
3
t
2
These are the nodes that are reachable from
node s.
s
2
4
5
3

25. Ford-Fulkerson Max Flow 1
1
2
2
2
1
2
s
2
4
5
3
t
Here is the optimal flow