This document summarizes several dense matrix algorithms for operations like matrix-vector multiplication, matrix-matrix multiplication, and solving systems of linear equations. For matrix-vector multiplication, it describes 1D and 2D row-wise partitioning approaches. The 2D approach has lower parallel runtime of O(log n) but requires n2 processes. A modified 2D approach uses block partitioning and has parallel runtime of O(n/√p + log p) when using p < n2 processes. 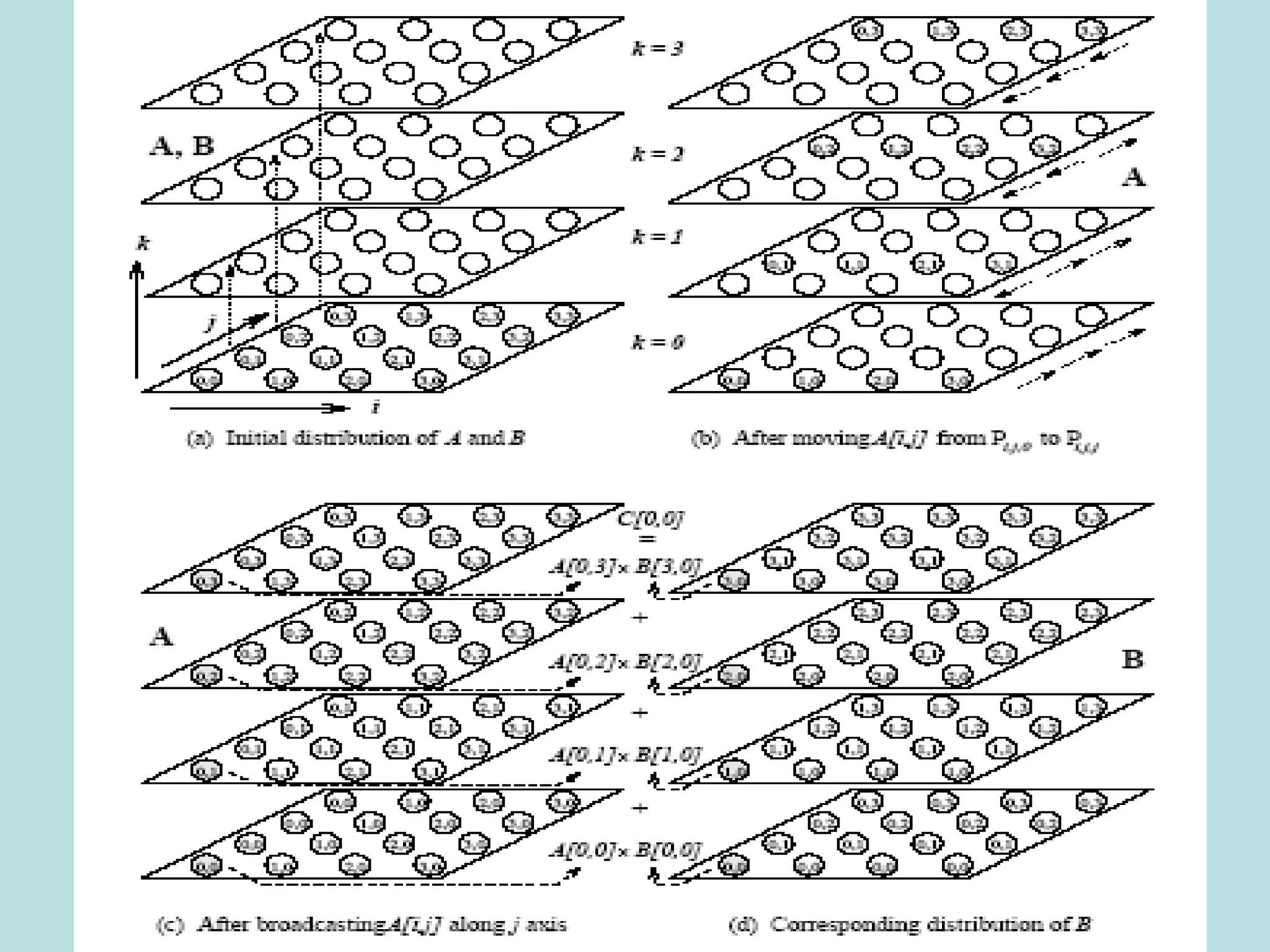For matrix-matrix multiplication, simple parallel and Canon's algorithms are described. Canon's algorithm has optimal O(n3) memory usage by rotating matrix blocks among processes. A DNS algorithm achieves optimal O(log n

1. Dense Matrix Algorithms
Carl Tropper
Department of Computer Science
McGill University

2. Dense
• Few non-zero entries
• Topics
– Matrix-Vector Multiplication
– Matrix-Matrix Multiplication
– Solving a System of Linear Equations

3. Introductory ramblings
• Due to their regular structure, parallel
computations involving matrices and vectors
readily lend themselves to data-
decomposition.
• Typical algorithms rely on input, output, or
intermediate data decomposition.
• Discuss one-and two-dimensional block,
cyclic, and block-cyclic partitionings.
• Use one task per process

4. Matrix-Vector Multiplication
• Multiply a dense n x n matrix A with an n
x 1 vector x to yield an n x 1 vector y.
• The serial algorithm requires n2
multiplications and additions.

5. Rowwise 1-D Partitioning

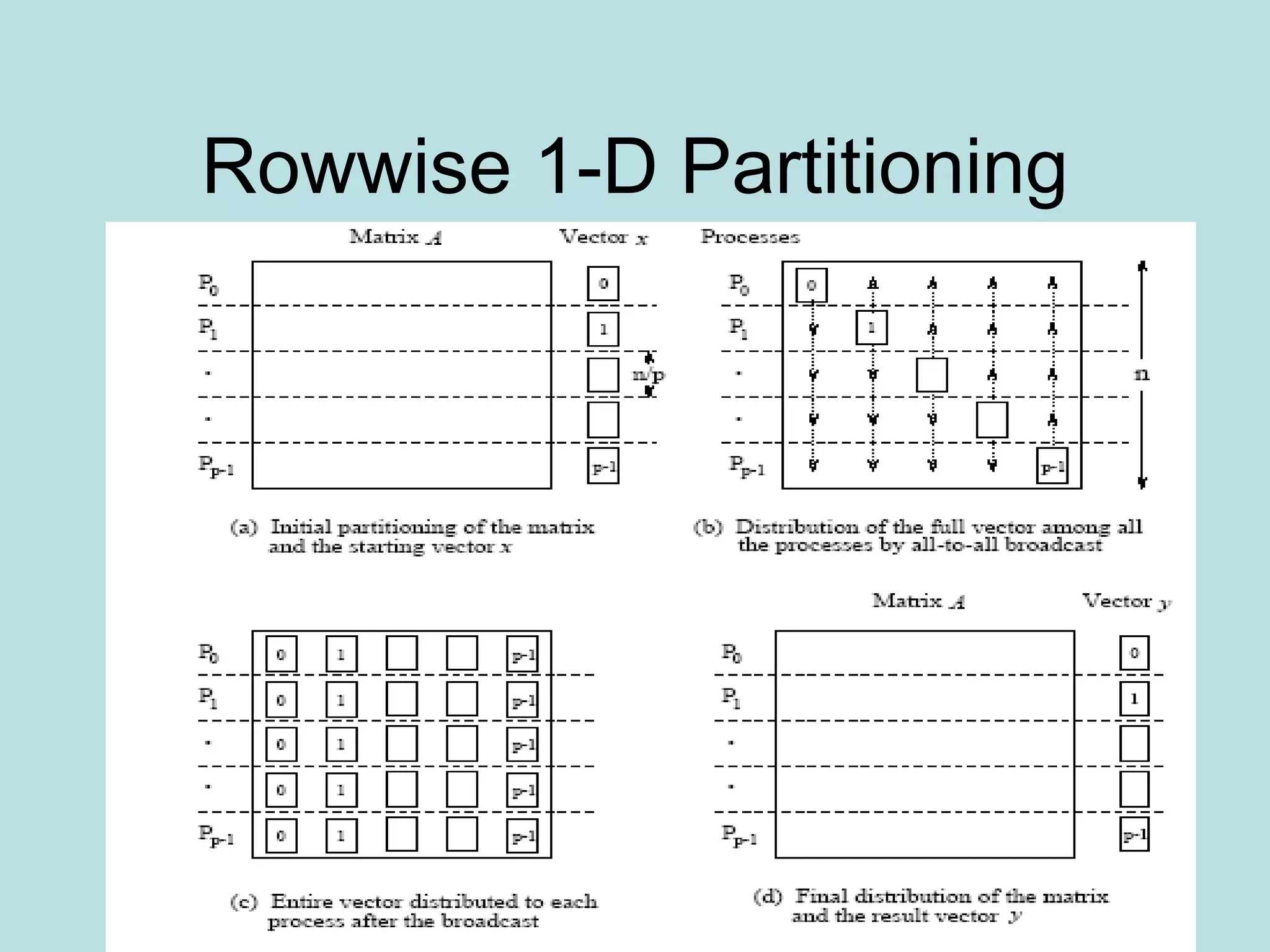
6. One row per process
• Each process starts with only one element of
x , need all-to-all broadcast to distribute all
the elements of x to all of the processes.
• Process Pi then computes
• The all-to-all broadcast and the computation
of y[i] both take time Θ(n) . Therefore, the
parallel time is Θ(n) .

7. P<N
• Use block 1D partitioning.
• Each process initially stores n/p complete
rows of the matrix and a portion of the vector
of size n/p.
• all-to-all broadcast takes place among p
processes and involves messages of size n/p
takes time tslog p + tw(n/p)(p-1)~tslog p+twn for
large p
• This is followed by n/p local dot products
• The parallel runtime is TP=n2/p + ts log p +twn
• pTP=n2 + pts log p + ptwn =>
• Cost optimal(pTp) if p=O(n)

8. Scalability Analysis
• We know that T0 = pTP - W, therefore, we
have,
• For isoefficiency, we have W = KT0, where K
= E/(1 – E) for desired efficiency E.
• TO=tsplog p + twnp
• W=n2=Ktwnp from tw term alone
=>W=n2=K2tw
2p2
• From this, we have W = O(p2) from the tw term
• There is also a bound on isoefficiency
because of concurrency. In this case, p < n,
therefore, W = n2 = Ω(p2).
• From these 2 bounds on W, the overall
isoefficiency is W = (p2).

9. 2-D Partitioning (naïve
version)
• Begin with one element per process
partitioning
• The n x n matrix is partitioned among n2
processors such that each processor owns a
single element.
• The n x 1 vector x is distributed in the last
column of n processors.Each processor has
one element.

10. 2-D Partitioning

11. 2-D Partitioning
• We must first align the vector with the matrix
appropriately.
• The first communication step for the 2-D
partitioning aligns the vector x along the
principal diagonal of the matrix.
• The second step copies the vector elements
from each diagonal process to all the
processes in the corresponding column using
n simultaneous broadcasts among all
processors in the column.
• Finally, the result vector is computed by
performing an all-to-one reduction along the
columns.

12. 2-D Partitioning
• Three basic communication operations are
used in this algorithm:
– one-to-one communication to align the vector
along the main diagonal,
– one-to-all broadcast of each vector element
among the n processes of each column, and
– all-to-one reduction in each row.
• Each of these operations takes Θ(log n) time
and the parallel time is Θ(log n) .
• There are n2 processes,so the cost (process-
time product) is Θ(n2 log n) ; hence, the
algorithm is not cost-optimal.

13. The less naïve version-fewer than n2
processes
• When using fewer than n2 processors, each
process owns an (n/√ p) x (n/ √ p)
block of the matrix.
• The vector is distributed in portions of (n/√ p)
elements in the last process-column only.
• In this case, the message sizes for the
alignment, broadcast, and reduction are all
(n/√ p)
• The computation is a product of an (n/√ p) x
(n/ √ p) submatrix with a vector of length (n/√
p) .

14. Parallel Run Time
• Sending message of size n/√p to diagonal
takes time ts + twn/√p
• Column-wise one to all broadcast takes (ts +
twn/√p)log √p using hypercube algorithm
• All to one reduction takes same amount of
time
• Assuming a multiplication and addition takes
unit time,each process spends n2/p
computing
• TP on next page

15. Next page
• TP=
• {computation} TP= n2/p +
• {aligning vector} ts +twn/√p+
• {columwise one to all broadcast }(ts + twn/ √ p)log√ p +
• {all to one reduction} ts + twn/ √ p)log √ p
• TP ~ n2/p + ts log p + tw (n/ √ p) log p

16. Scalability Analysis
• From W=n2, expression for TP, and TO=pTP-
W, TO=tsp log p + twn p log p
• As before, find out what each term
contributes to W
• W=Ktsp log p
• W=n2=Ktwn√plog p=>n=Ktw √p log p=>
n2=K2tw
2 p log 2p=>
• W=K2tw
2 p log2 p (**)
• Concurrency is n2=>p=O(n2)=>n2= Ω(p) and
• W= Ω(p)
• The tw term dominates (**) everything =>
• W= (p log2 p )

17. Scalability Analysis
• Maximum number of processes which can be
used cost-optimally for a problem of size W is
determined by p log2 p= O(n2)
• After some manipulation, p=O(n2/log2n),
• Asymptotic upper bound on the number of
processes which can be used for cost-otpimal
solution
• Bottom line:2-D partitioning is better than 1-D
because:
• It is faster!
• It has a smaller isoefficiency function-get the same
efficiency on more processes!

18. Matrix-Matrix multiplication
• Standard serial algorithm involves taking the
dot product of each row with each column,
has complexity of n3
• Can also use q x q array of blocks, where
each block is (n/q x n/q). This yields q3
multiplications and additions of the sub-
matrices. Each of the sub-matrices involves
(n/q)3 additions and multiplications.
• Paralellize the q x q blocks algorithm.

19. Simple Parallel Algorithm
• A and B are partitioned into p blocks, i.e. AIJ ,
BIJ of size (n/√p x n/√p)
• They are mapped onto a √p x √p mesh
• PI,J stores AI,J and BI,J and computes CI,J
• Needs AI,K and BJ,K sub-matrices 0 k< √p
• All to all broadcast of A’s blocks done on each
row and of B’s blocks on each column
• Then multiply A’s and B’s

20. Scalability
• 2 all to all broadcasts of process mesh
• Messages contain submatrices of n2/p elements
• Communication time is 2(ts log (√p) + tw (n2/p)( p-1)
{hypercube is assumed}
• Each process computes C I,J-takes p
multiplications (n/√p x n/√p) submatrices,
taking n3/p time.
• Parallel time TP= n3/p + ts log p + 2 tw n2/√p
• Process time product=n3+tsplog p+2twn2 √p
• Cost optimal for p=O(n2)

21. Scalability
• The isoefficiency is O(p1.5) due to
bandwidth term tw and concurrency
• Major drawback-algorithm is not
memory optimal-Memory is (n2 √p), or
√p times the memory of the sequential
algorithm

22. Canon’s algorithm
• Idea: schedule the computations of the
processes of the ith row such that at any
given time each process uses a different
block Ai,k.
• These blocks can be systematically rotated
among the processes after every submatrix
multiplication so that every process gets a
fresh Ai,k after each rotation
• Use same algorithm for columns=>no
process holds more then one bock at a time
• Memory is (n2)

23. Canon shift

24. Performance
• Max shift for a block is √p-1.
• 2 shifts (row and column) require 2(ts+twn2/p)
• P shifts=>√p2(ts+twn2/p) total comm time
• The time for multiplying p matrices of size
(n/√p) x (n/√p) is n3/p
• TP= n3/p+√p2(ts+twn2/p)
• Same cost-optimality condition as simple
algorithm and same iso function.
• Difference is memory!!

25. DNS Algorithm
• Simple and Canon
• Use block 2-D partitioning of input and output matrices
• Use a max of n2 processes for nxn matrix multiplication
• Have Ω(n) run time because of (n3) ops in the serial
algorithm
• DNS
• Uses up to n3 processes
• Has a run time of (log n) using Ω(n3/log n) processes

27. DNS Algorithm
• Assume an n x n x n mesh of processors.
• Move the columns of A and rows of B and
perform broadcast.
• Each processor computes a single add-
multiply.
• This is followed by an accumulation along the
C dimension.
• Addition along C takes time (log n) =>
• Parallel runtime is (log n)
• This is not cost optimal. It can be made cost
optimal by using n / log n processors along
the direction of accumulation

28. Cost optimal DNS with fewer then n3
• Let p=q3 for q<n
• Partition the 2 matrices into blocks of
size n/q x n/q
• Have a q x q square array of blocks

29. Performance
• 1-1 communication takes ts+tw(n/q)2
• 1-all broadcast takes tslog q+tw(n/q)2 for each
matrix
• Last all-1 reduction takes tslog q+tw(n/q)2log q
• Multiplication of n/q x n/q submatrices takes
(n/q)3
• TP~(n/q)3 + tslogp+tw(n2/p2/3)logp=>cost is
n3+tsplogp+twn2p1/3logp
• Isoefficiency function is (p(logp)3)
• Algorithm is cost optimal for p=O(n3/(log n)3)

30. Linear Equations

31. Upper Triangular Form
•Idea is to convert the equations into this form,
and then back substitute (i.e. go up the chain)

32. Principle behind solution
• Can make use of elementary operations
on equations to solve them
• Elementary operations are
• Interchanging two rows
• Replace any equation by a linear combination
of any other equation and itself

33. Code for Gaussian Elimination

34. What the code is doing

35. Complexity of serial Gaussian
• n2/2 divisions (line 6 of code)
• n3/3-n2/2 subtractions and
multiplications (line 12)
• Assuming all ops take unit time, for
large enough n have W=2/3 n3

36. Parallel Gaussian
• Use 1-D Partitioning
• One row per process

37. 1-D Partitioning

38. Parallel 1-D
• Assume p = n with each row assigned to a processor.
• The first step of the algorithm normalizes the row.
This is a serial operation and takes time (n-k) in the
kth iteration.
• In the second step, the normalized row is
broadcast to all the processors. This takes time
(ts+tw(n-k-1))log n
• Each processor can independently eliminate this row
from its own. This requires (n-k-1) multiplications and
subtractions.
• The total parallel time can be computed by summing
from k = 1 … n-1 as TP=3/2n(n-1)+tsnlog n+1/2twn(n-
1)log n.
• The formulation is not cost optimal because of the tw
term.

39. Parallel 1-D with Pipelining
• The (k+1)st iteration starts only after kth
iteration completes
• In each iteration, all of the active processes
collaborate together
• This is a synchronous algorithm
• Idea: Implement algorithm so that no process
has to wait for all of its predecessors to finish
their work
• The result is an asynchronous algorithm,
which makes use of pipelining
• Algorithm turns out to be cost-optimal

40. Pipelining
• During the kth iteration, P k sends part of the
kth row to Pk+1, which forwards it to Pk+1,
which…..
• P k+1 can perform the elimination step without
waiting for the data finish its journey to the
bottom of the matrix
• Idea is to get the maximum overlap of
communication and computation
• If a process has data destined for other processes, it
sends it right away
• If the process can do a computation using the data it has,
it does so

41. Pipeline for 1-D, 5x5

42. Pipelining is cost optimal
• The total number of steps in the entire
pipelined procedure is Θ(n).
• In any step, either O(n) elements are
communicated between directly-connected
processes, or a division step is performed on
O(n) elements of a row, or an elimination step
is performed on O(n) elements of a row.
• The parallel time is therefore O(n2)
• Since there are n processes, the cost is O(n3)
• Guess what,cost optimal!

43. Pipelining 1-D with p<n
• Pipelining algorithm can be easily
extended
• N x N matrix
• n/p processes per processor
• Example on next slide
• P=4
• 8 x8 matrix

44. Next slide

45. Analysis
• In the kth iteration, a processor with all rows
belonging to the active part of the matrix
performs (n – k -1) / np multiplications and
subtractions during elimination step of the kth
iteration.
• Computation dominates communication at
each iteration (n-(k+1)) words are
communicated during iteration k (vs (n-
(k+1)/np computation ops)
• The parallel time is 2(n/p)∑k=0
n-1 (n-k-1) ~
n3/p.
• The algorithm is cost optimal, but the cost is
higher than the sequential run time by a
factor of 3/2.

46. Fewer then n processes
• The parallel time is 2(n/p)∑k=0
n-1 (n-k-1) ~
n3/p.
• The algorithm is cost optimal, but the cost is
higher than the sequential run time by a
factor of 3/2.
• Inefficiency due to unbalanced load
– In the figure on next slide,1 process is idle, 1 is
partially active, 2 are fully active
• Use cyclic block distribution to balance load

47. Block and cyclic mappings

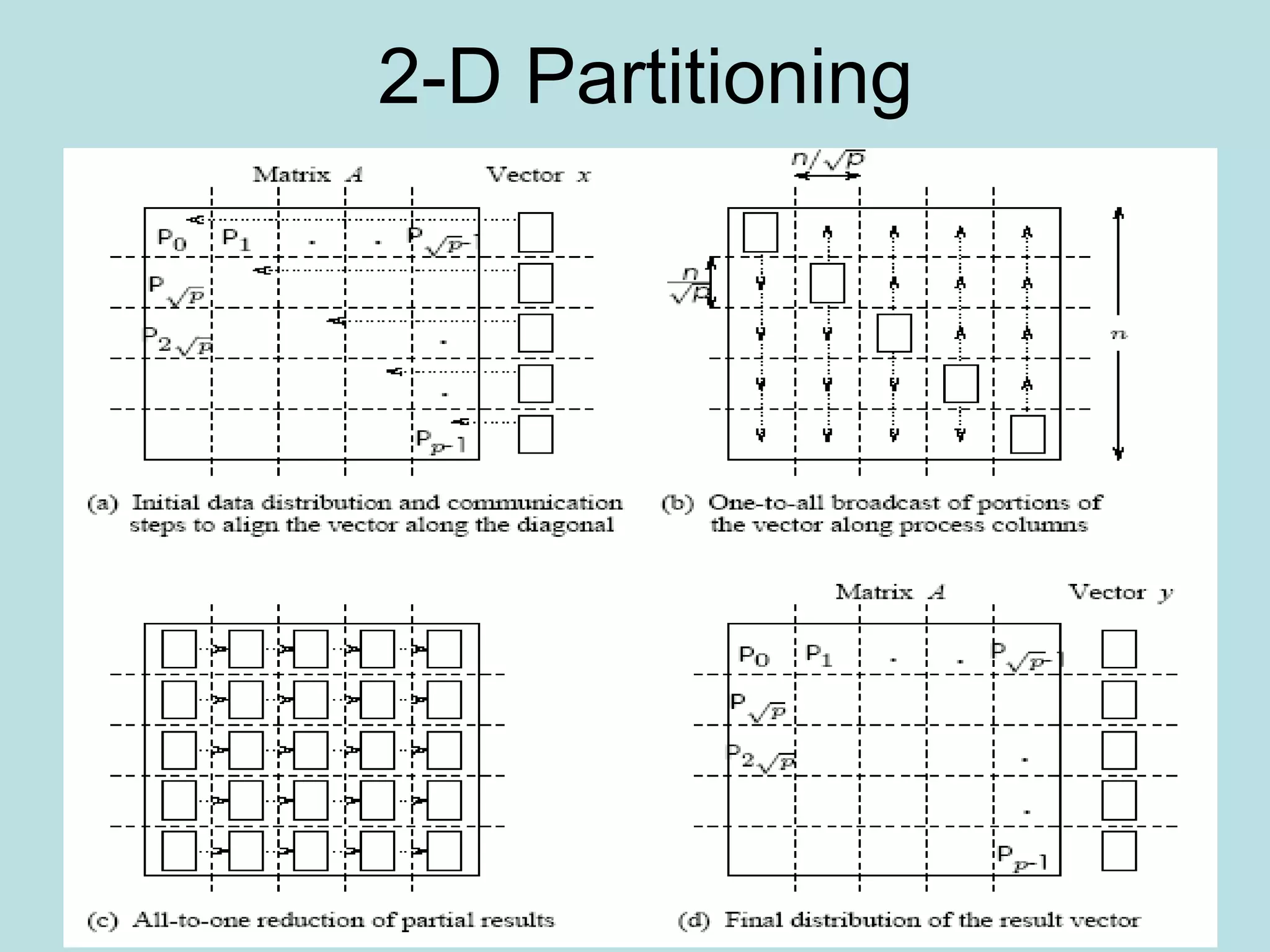
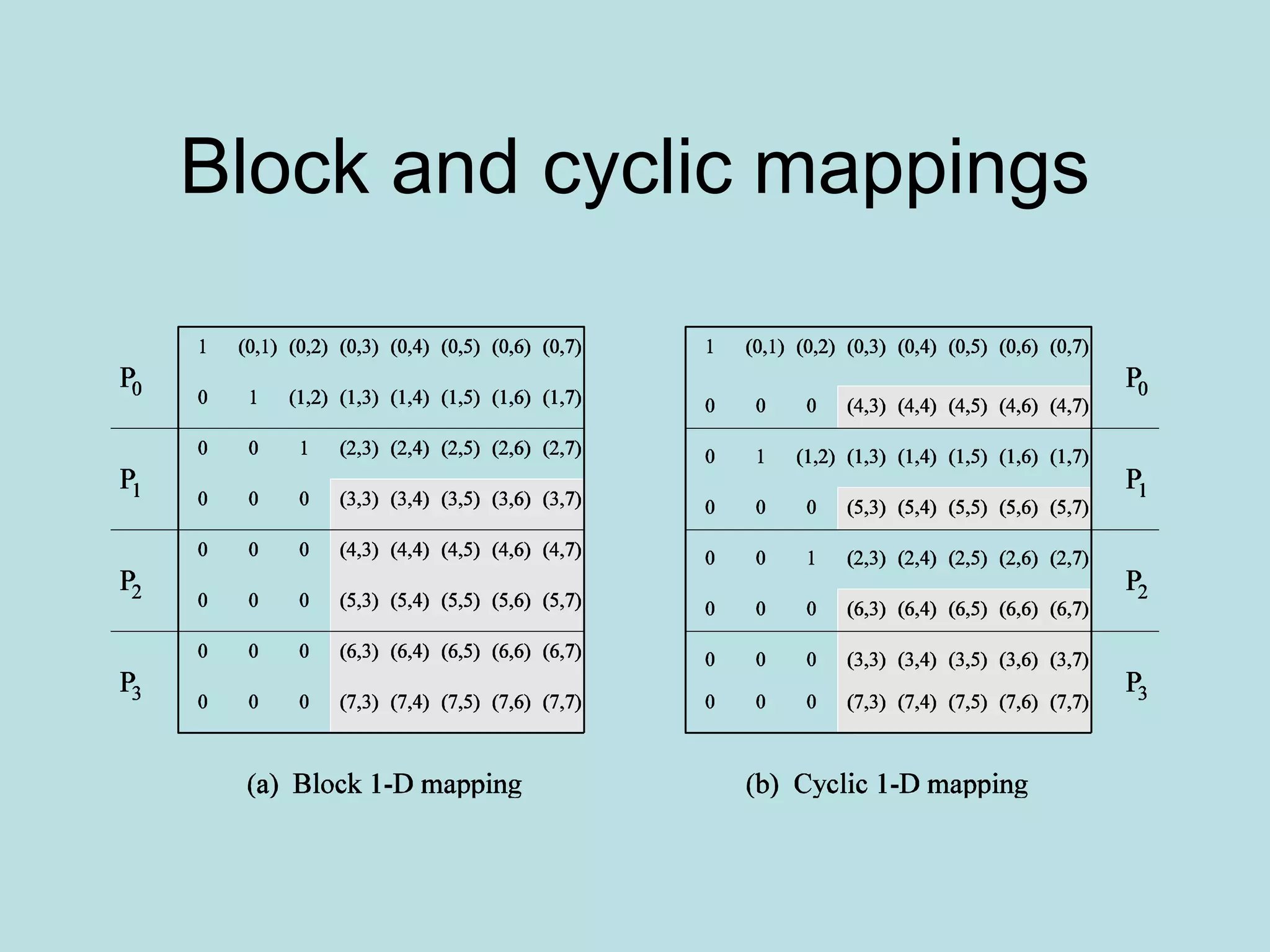
48. 2-D Partitioning
• A[i,j] is n x n and is mapped to n x n mesh-
A[i,j] goes to P I,J
• The rest is as before, only the communication
of individual elements takes place between
processors
• Need one to all broadcast of A[i,k] along ith
row for k≤ i<n and one to all broadcast of
A[k,j] along jth column for k<j<n
• Picture on next slide
• The result is not cost optimal

49. Picture
K=3 for 8 x8 mesh

50. Pipeline
• If we use synchronous broadcasts, the results
are not cost optimal, so we pipeline the 2-D
algorithm
• Principle of the pipelining algorithm is the
same-if you can compute or communicate, do
it now, not later
– P k,k+1 can divide A[k,k+1] by A[k,k] before A[k,k+1]
reaches P k,n-1 {the end of the row}
– After A[k,j] performs the division, it can send the
result down column j without waiting
• Next slide exhibits algorithm for 2-D pipelining

51. 2-D pipelining algorithm

52. Pipelining-the wave
• The computation and communication for each
iteration moves through the mesh from top-
left to bottom-right like a wave
• After the wave corresponding to a certain
iteration passes through a process, the
process is free to perform subsequent
iterations.
• In g, after k=0 wave passes P 1,1 it starts k=1 iteration by
passing A[1,1] to P 1,2.
• Multiple wave that correspond to different
iterations are active simultaneously.

53. The wave-continued
• If each step (division, elimination, or
communication) is assumed to take constant
time, the front moves a single step in this
time. The front takes Θ(n) time to reach Pn-1,n-
1.
• Once the front has progressed past a
diagonal processor, the next front can be
initiated. In this way, the last front passes the
bottom-right corner of the matrix Θ(n) steps
after the first one.
• The parallel time is therefore O(n) , which is
cost-optimal.

54. Fewer then n2 proceses
• In this case, a processor containing an active
part of the matrix performs n2/p multiplications
and subtractions, and communicates n/ √p
words along its row and its column.
• The computation dominates communication
for n >> p.
• The total parallel run time of this algorithm is
(2n2/p) x n, since there are n iterations.
• Process time product=2n3/p x p= 2n3
• This is three times the serial operation count!

55. Fewer

56. Load imbalance
• Same problem as with 1-D mapping-an
uneven load distribution
• Same solution-cyclic partitioning

57. Load imbalance and a cyclic solution

58. Comparison
• Pipelined version takes (n3/p) time on
p processes for both 1-D and 2-D
versions
• 2-D partitioning can use more
processes O(n2) then 1-D partitioning
O(n) for an n x n matrix => 2-D version
is more scalable