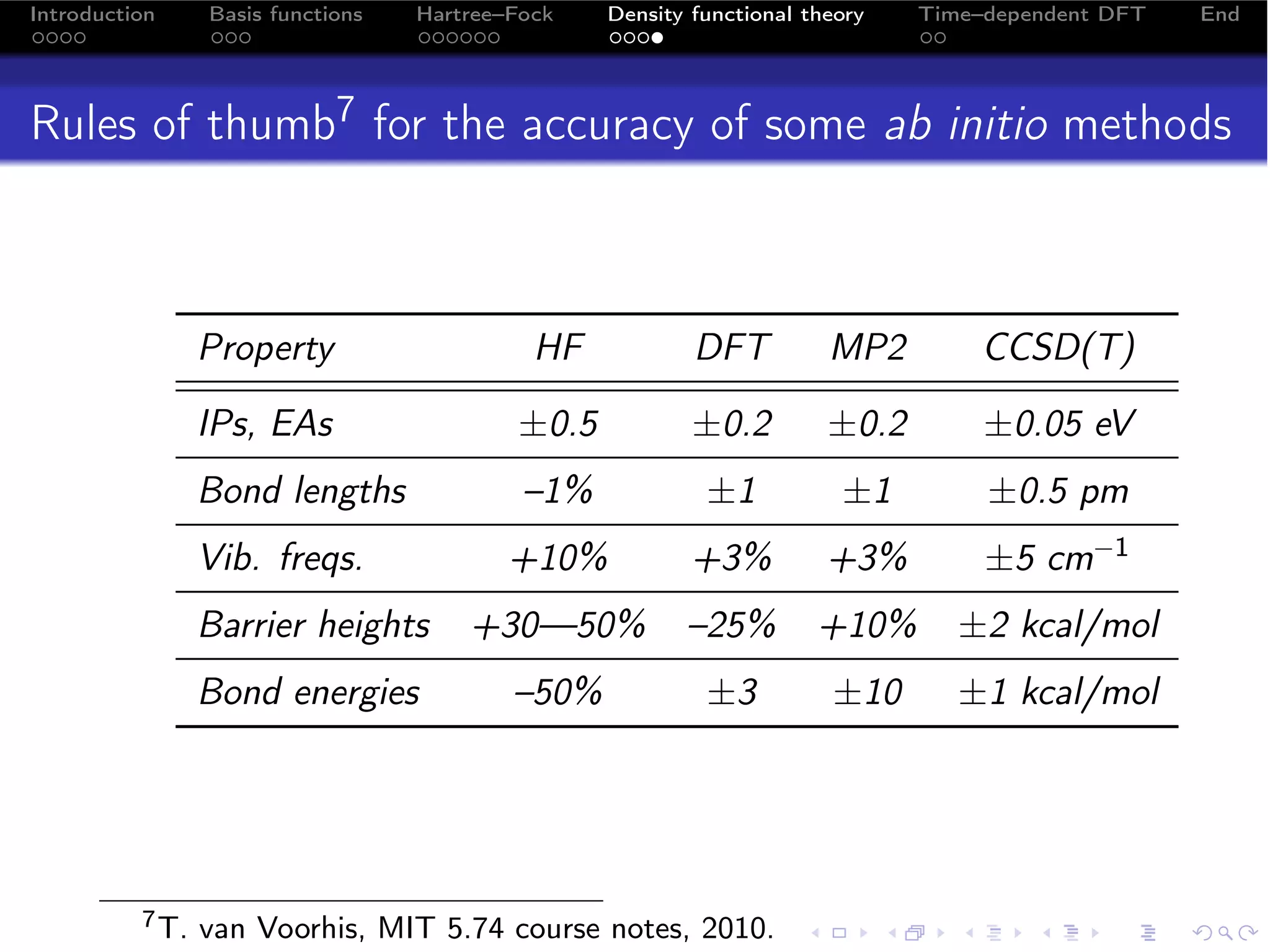
The document provides an overview of time-dependent density functional theory (TDDFT) for computing molecular excited states. It begins with an introduction to the Born-Oppenheimer approximation and variational principle. It then discusses the Hartree-Fock and Kohn-Sham equations as self-consistent field methods for calculating ground states, and linear response theory for calculating excited states within TDDFT. The contents section outlines the topics to be covered, including basis functions, Hartree-Fock theory, density functional theory, and time-dependent DFT.

1. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Looking into the black box
Computing molecular excited states with time-dependent density
functional theory (TDDFT)
Jiahao Chen and Shane Yost
Van Voorhis group, MIT Chemistry
2010-03-12

2. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Disclaimer
This is a very superficial survey of two ideas:
1 Self–consistent field methods for ground state calculations, and
2 Linear response theory for excited state calculations.
There will be math and jargon.
Most of it is optional.
The math is not presented in the most general case.
We won’t have time today to discuss calculating observables and
numerical results.

3. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Disclaimer
This is a very superficial survey of two ideas:
1 Self–consistent field methods for ground state calculations, and
2 Linear response theory for excited state calculations.
There will be math and jargon.
Most of it is optional.
The math is not presented in the most general case.
We won’t have time today to discuss calculating observables and
numerical results.

4. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Disclaimer
This is a very superficial survey of two ideas:
1 Self–consistent field methods for ground state calculations, and
2 Linear response theory for excited state calculations.
There will be math and jargon.
Most of it is optional.
The math is not presented in the most general case.
We won’t have time today to discuss calculating observables and
numerical results.

5. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Statement of the Problem (Born–Oppenheimer)
Given that we know where the atomic nuclei are, where are the
electrons?
ˆ
H (r1 , . . . , N ) Ψn (r1 , . . . , N ) = En Ψn (r1 , . . . , N )
r r r (1)
ˆ
H is the electronic, or Born–Oppenheimer Hamiltonian:
N
1
ˆ
H = ∑ hi + ∑ |i −j |
ˆ
r r
(1-e + e–e repulsion) (2)
i=1 ij
1
h1 = − ∇2 + vext (r ) (kinetic energy + external pot.)(3)
ˆ
2 1
M
ZI
vext (r ) = − ∑
(e–nucleus interaction)
(4)
I =1 RI −
r

6. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Statement of the Problem (Born–Oppenheimer)
Given that we know where the atomic nuclei are, where are the
electrons?
ˆ
H (r1 , . . . , N ) Ψn (r1 , . . . , N ) = En Ψn (r1 , . . . , N )
r r r (1)
ˆ
H is the electronic, or Born–Oppenheimer Hamiltonian:
N
1
ˆ
H = ∑ hi + ∑ |i −j |
ˆ
r r
(1-e + e–e repulsion) (2)
i=1 ij
1
h1 = − ∇2 + vext (r ) (kinetic energy + external pot.)(3)
ˆ
2 1
M
ZI
vext (r ) = − ∑
(e–nucleus interaction)
(4)
I =1 RI −
r

7. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Practical solution of the Schrödinger equation
ˆ
H (r1 , . . . , N ) Ψn (r1 , . . . , N ) = En Ψn (r1 , . . . , N )
r r r
What approximations do we need to solve this practically?
Approximate wavefunction
Variational ansätze
Orbital (one–particle) approximation
Basis set approximation
Approximate Hamiltonian
Noninteracting particle / mean field approximation
In DFT: approximations to exchange–correlation
Linear response approximation (for excited states)

8. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Contents
1 Basis functions
2 Hartree–Fock
3 Density functional theory
4 Time–dependent DFT

9. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Variational principle and ansätze
We don’t know the exact solution to the many–body Schrödinger
equation. But we can make an educated guess, an ansatz (pl.
ansätze).
Variational principle
An approximate wavefunction Ψ (a, b, . . . ) always yields a higher
energy than the exact solution Ψ0 , i.e.
Ψ |H| Ψ Ψ0 |H| Ψ0
≥ E0 = (5)
Ψ|Ψ Ψ0 |Ψ0
This reduces a differential equation into an optimization problem
for the numerical parameters a, b, . . .

10. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Bases in vector spaces
A basis describes axes, allowing coordinates to be defined.
Example
R3 has basis {ex , ey , ez }. Numbers (x, y , z) can be assigned as
coordinates to a point with position vector v = xex + y ey + zez .
A less obvious example:
Example
Computer monitors use RGB color space, with basis {red, green,
blue}. For example, a kind of purple is described by purple = 1 red
2
+ 1 blue and has coordinates 1 , 0, 1 in color space.
2 2 2

11. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Bases in function spaces
Basis functions describe “axes” in function space. If you have a
collection of mutually orthogonal, real functions φ1 (x) , . . . , φn (x)
that span the entire space of functions, then
f (x) = ∑ ci φi (x) (7)
i
whose coefficients are given by projections onto the basis
N f (x) φi (x) dx
´
ci = R´ 2
(8)
RN φi (x) dx
Then the function f has “coordinates” (c1 , c2 , . . . ) in the basis
spanning the function space.
Example
Functions over [−π, π] have Fourier series expansions, whose basis
functions are 1, sin x, cos 2x, sin 3x, cos 4x, . . .

12. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
The independent particle ansatz: from many to one
Let’s try to solve the many–body Schrödinger equation
ˆ
H (r1 , . . . , N ) Ψn (r1 , . . . , N ) = En Ψn (r1 , . . . , N )
r r r
As a first guess for Ψn , assume that it is factorizable into a Hartree
product of one–particle wavefunctions (orbitals) 1
Ψ (r1 , . . . , N ) = φ1 (r1 ) · · · φN (rN )
r (9)
However, this wavefunction is not antisymmetric (no Pauli
exclusion). The simplest fermionic ansatz is the Slater determinant2
φ1 (r1 ) · · · φ1 (rN )
1
Ψ (r1 , . . . , N ) = √
r .
. .. .
.
(10)
. . .
N!
φN (r1 ) · · · φN (rN )
1 D. R. Hartree, Proc. Cam. Phil. Soc. 24 (1928) 89; 111; 426
2 J. C. Slater, Phys. Rev. 34 (1929) 1293

13. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
The Hartree–Fock equation
Using the ansatz that the many–body wf is a Slater determinant,
the variational principle leads to3 the Hartree–Fock equation
Fi φi (r ) = εi φi (r )
ˆ (11)
ˆ
Fi = hi + ∑ Jj − Kj (Fock operator)
ˆ ˆ ˆ (12)
j
J is the classical Coulomb potential = Hartree potential vH .
K is the exchange interaction with no classical analogue.
(absent in Hartree theory)
3 A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, 1982, Ch. 3

14. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Hartree–Fock is a mean field theory
Electrons in Hartree–Fock feel an electric
field of potential Φ = ∑N Jj − Kj .
ˆ
j=1
ˆ ˆ
The mean field is a self–consistent field
The electron–electron interactions are
approximated by the interaction between an
electron and this electric field. This field
depends on the orbitals, yet also helps
determines them.
Correlation energy = the error in
Hartree–Fock energy (wrt exact)

15. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Roothaan–Hall equation
If we project the Hartree–Fock equation onto a basis {χ1 , . . . , χP },
P
φi = ∑ Ciα χα (13)
α=1
we get the Roothaan–Hall equation
FC = ESC (14)
which is a generalized eigenvalue equation.
Atomic orbitals = spatially localized basis {χ1 , . . . , χP },
Molecular orbitals = eigenvectors of the Roothaan–Hall
equation

16. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Basis sets
There are many choices for the atomic basis {χ1 , . . . , χP }:
Plane waves: great for periodic systems (solids), inefficient for
molecules (and other systems without translational symmetry)
Wannier functions
Slater orbitals: use hydrogenic orbitals, nice theoretical
properties. In practice the Fock matrix is very difficult to
calculate. Not widely used today, except in ADF.
Gaussian orbitals: popular for molecules. Easy to calculate.
Pople basis sets: STO-3G, 3–21G, 6–31G*, 6–311+G**,...
Dunning–Hays correlation–consistent basis sets: cc-pVDZ,
aug-cc-pVQZ, d-aug-cc-pVTZ, ...
Others, e.g. wavelets, adaptive quadrature grids...

17. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Post–Hartree–Fock methods
Many methods to treat correlation use Hartree–Fock as a starting
point:
Perturbative corrections: Møller–Plesset (MP2,...),...
Configuration interaction: CISD, FCI,...
Coupled–cluster: CCSD, CCSD(T),...

18. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Kohn–Sham equations
In 1965, Kohn and Sham proposed a noninteracting system for use
with density functional theory.4 This turns out to look like
Hartree–Fock theory with a correction for electronic correlation.
The resulting one–particle equation is written as:
1 2
Hs φi (r ) = − ∇s + vs (r ) φi (r ) = εi φi (r )
(15)
2
where − 1 ∇2 is the noninteracting part of the kinetic energy and vs
2 s
is the Kohn–Sham potential:
vs (r ) = vext (r ) + vH (r ) + vxc (r )
(16)
The exchange–correlation potential vxc has three contributions:
exchange, correlation, and a correction to the kinetic energy.
4 W. Kohn and L. J. Sham, Phys. Rev. 140, 1965, A1133

19. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Kohn–Sham is a density functional theory
The Kohn–Sham equation is equivalent to finding the density ρ
that minimizes the energy functional
ˆ
E [ρ] = vext (r ) ρ (r ) d + Ts [ρ] + VH [ρ] + Exc [ρ]
r (17)
R3
1 N
ˆ
Ts [ρ] = − ∑ φi (r ) ∇2 φi (r ) d
r (18)
2 i=1 R3
1 ρ (r ) ρ (r )
ˆ
VH [ρ] = + d d
r r (19)
2 R6 |r −
r |
where the density is constructed from
N
ρ (r ) =
∑ |φi ( )|2 = ∑
r Ci µ Ciν χµ (r ) χν (r )
(20)
i=1 µνi

20. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Density functionals
The form of the exchange–correlation functional Exc is unknown.
There are many, many approximations to it:
“Jacob’s Ladder” of approximations to Exc [ρ]:5
1 Exc [ρ] LDA X α, LDA,...
2 Exc [ρ, ∇ρ] GGA BLYP, PBE, PW91...
3 Exc [ρ, ∇ρ, τ] meta–GGA VSXC, TPSS, ...
4 Exc [ρ, ∇ρ, τ, {φ }o ] hybrids 6 ,... B3LYP, PBE0,...
5 Exc [ρ, ∇ρ, τ, {φ }] fully nonlocal -
LDA, local density approximation; GGA, generalized gradient
approximation; τ, kinetic energy density; {φ }o , occupied
orbitals; {φ }, all orbitals.
Green function expansions for Exc : GW, Görling–Levy PT,...
Approximations to kinetic energy: Thomas–Fermi, von
Wiezsäcker,...
5 M. Casida, http://bit.ly/casidadft
6 Hybrid functionals mix in Hartree–Fock exchange.

21. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Rules of thumb7 for the accuracy of some ab initio methods
Property HF DFT MP2 CCSD(T)
IPs, EAs ±0.5 ±0.2 ±0.2 ±0.05 eV
Bond lengths –1% ±1 ±1 ±0.5 pm
Vib. freqs. +10% +3% +3% ±5 cm−1
Barrier heights +30—50% –25% +10% ±2 kcal/mol
Bond energies –50% ±3 ±10 ±1 kcal/mol
7 T. van Voorhis, MIT 5.74 course notes, 2010.

22. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Polarizabilities as linear response
Polarizability: a dipole’s response to an electric field
The isotropic ground state polarizability can be calculated exactly
from time–dependent perturbation theorya
∂ ˆ
r f0→n
α (ω) =
¯ =∑ 2 (21)
∂ ε (ω) n ω0→n − ω
2
where ω0→n is excitation frequency (energy) to state n and f0→n
are oscillator strengths. This is a sum over states (SOS) formula.
a Kramers, H. A.; Heisenberg, W. (1925) Z. Phys. 31: 681–708.
Dirac, P. A. M. (1927) Proc. Roy. Soc. Lond. A 114: 243–265; 710–728.
Linear response is a quest for resonances
Resonant frequencies of the system’s reaction to small
perturbations says something about its excitation spectrum.

23. Introduction Basis functions Hartree–Fock Density functional theory Time–dependent DFT End
Resonances in density response
Main idea
Using the density response δ ρ to a time–dependent perturbing
potential δ v , we can back out what the excited state characters are.
Consider the generalized susceptibility χ (t) as defined by
ˆ ˆ
δ ρ (r , t) =
χ , , t − t δ v , t dt d
r r r r (22)
R R3
A SOS formula for the Fourier–transformed susceptibility χ can be
˜
derived, and furthermore the conditions for resonance can be
expressed as an eigenvalue equation that takes the form8
A B X I 0 X
=ω (23)
B ∗ A∗ Y 0 −I Y
X is the hole–particle (occupied–virtual) density change
Y is the particle–hole (virtual–occupied) density change
8 M. Casida, in Recent Advances in Density Functional Methods I, p. 155

24. End of Part I