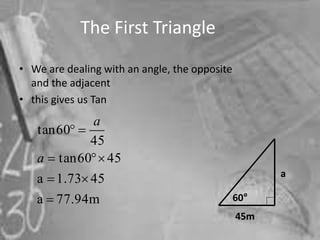
Trigonometry is a branch of mathematics that deals with relationships between angles and sides of right triangles. It originated in ancient Greece. There are three basic trigonometric ratios - sine, cosine, and tangent - that relate the measures of angles to the lengths of sides in a right triangle. To solve problems using trigonometric ratios, one identifies the appropriate ratio based on the given and unknown sides, then substitutes the known values into the ratio formula and solves for the unknown.

1. It’s a branch of mathematics
that deals with the study of right
angled triangles and there
applications.
It is originated in Greek

2. When you have a right triangle there are 5
things you can know about it..
• the lengths of the sides (A, B, and C)
• the measures of the acute angles (a and b)
• (The third angle is always 90 degrees)
• If you know two of the sides, you can use the Pythagorean
theorem to find the other side
• And if you know either angle, a or b, you can subtract it
from 90 to get the other one: a + b = 90
A
C
B
a
b

5. SOHCAHTOA
Adjacent
A
B
Opposite
Hypotenuse
Here is a way to remember how to
make the 3 basic Trig Ratios
1) Identify the Opposite and Adjacent sides for
the appropriate angle
2) SOHCAHTOA is pronounced “Sew Caw Toe A” and it means
Sin is Opposite over Hypotenuse, Cos is Adjacent over Hypotenuse, and Tan is
Opposite over Adjacent
Put the underlined letters to make
SOH-CAH-TOA

6. Trig ratios/
angles
0˚ 30˚ 45˚ 60˚ 90˚
Sin 0 1/2 1
Cos 1 1/2 0
Tan 0 1 n.d.
2
321
2
3
31
2
1
3

7. 3
Lets try an Example
 You look up at an
angle of 60° at the
top of a tree that is
10m away. Find the
height of the tree.

10. What are the steps for doing one
of these questions?
1. Make a diagram if needed
2. Determine which angle you are working with
3. Label the sides you are working with
4. Decide which formula fits the sides
5. Substitute the values into the formula
6. Solve the equation for the unknown value
7. Does the answer make sense?

11. 10m
60˚
?

12. ????????????????????????????60tan
60tan10
10
60tan



opp
opp
SOLUTION

14. Now Can U calculate?
23.17
310
310
60tan10
10
60tan





tree
opp
opp
opp
opp

15. Take another example…
• Lucretia drops her walkman
off the Leaning Tower of Pisa
when she visits Italy
• It falls to the ground 2
meters from the base of the
tower
• If the tower is at an angle of
60° to the ground, how far
did it fall?

16. First draw a triangle
• What parts do we have?
• We have an angle
• We have the Adjacent
• We need the opposite
• Since we are working with
the adj and opp, we will use
the tan formula
2m
60°
B

17. So lets calculate
2m
60°
B
mopp
opp
opp
opp
opp
adj
opp
46.3
32
23
260tan
2
60tan
60tan







18. Two Triangle Problems
• Although there are two triangles, you only
need to solve one at a time
• The big thing is to analyze the system to
understand what you are being given
• Consider the following problem:
• You are standing on the roof of one building
looking at another building, and need to find
the height of both buildings.

19. Draw a diagram
• You can measure
the angle 45° down
to the base of other
building and up 60°
to the top as well.
You know the
distance between
the two buildings is
45m
60°
45°
45m

20. Break the problem into two triangles.
• The first triangle:
• The second triangle
• note that they share a
side 45m long
• a and b are heights!
60°
45m
45°
b
a

21. The First Triangle
• We are dealing with an angle, the opposite
and the adjacent
• this gives us Tan
60°
45m
a
77.94ma
451.73a
4560tan
45
60tan




a
a

22. The second triangle
• We are dealing with an angle, the opposite and the
adjacent
• this gives us Tan
45m
45°
b
45mb
451b
4545tan
45
45tan




b
b

23. What does it mean?
• Look at the diagram now:
• the short building is 45m
tall
• the tall building is 77.94m
plus 45m tall, which equals
118.94m tall
60°
45°
45m
77.94m
45m