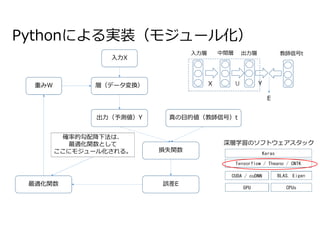
鉄板トピックの誤差逆伝播について４０分ほど話しました。 ❏ 多層パーセプトロン ❏ 勾配降下法 ❏ リバースモード自動微分 ❏ 確率的勾配降下法 ❏ 実装（モジュール化） Rumelhart, David E.; Hinton, Geoffrey E., Williams, Ronald J. (8 October 1986). “Learning representations by back-propagating errors”. Nature 323 (6088): 533–536. doi:10.1038/323533a0.

1. 解説#78 誤差逆伝播
https://www.youtube.com/user/blinknetmonitoring
安藤類央

2. 誤差逆伝播(Backpropagation)
❐ 多層パーセプトロンを学習させる方法
❐ すべてのディープラーニングのモデルにおいて必要となる手法
以下のアルゴリズムによって構成される。
❐勾配降下法
❐リバースモード自動微分
❐確率的勾配降下法
前提:回帰と分類、パーセプトロンとADALINEの説明が終わっている。

3. MLP (Multi Layer Perceptron: 多層パーセプトロン）
∑
x[j]
w[j][k]
n[k] u[k]
②活性関数
b1
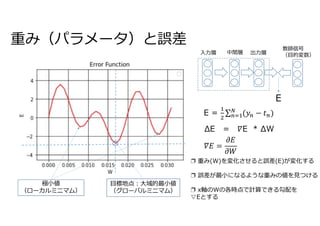
入力x 出力u 出力y
入力層(x) 中間層(u) 出力層
(y)
教師信号t
誤差E
教師信号（目的変数）
E =
③ 損失(誤差）関数
=
b2
① 総入力（加重総和）関数
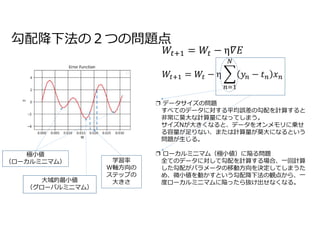
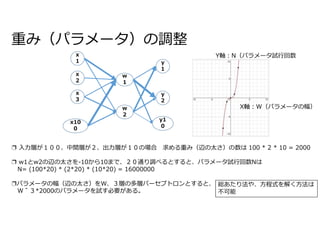
多層パーセプトロンは、３つの層、３つの関数から構成される。
① 総入力（加重総和）関数
② 活性関数
③ 損失（誤差）関数
重みW1 重みW2
ステップ関数の話
パーセプトロンの内部構造

4. 重み（パラメータ）と誤差
目標地点:大域的最小値
（グローバルミニマム）
❐ 重み(W)を変化させると誤差(E)が変化する
❐ 誤差が最小になるような重みの値を見つける
❐ x軸のWの各時点で計算できる勾配を
▽Eとする
極小値
（ローカルミニマム）
ΔE = E * ΔW
E =
入力層 中間層 出力層
教師信号
（目的変数）
E

5. 重み（パラメータ）の調整
x
1
x
2
x
3
x10
0
w
2
w
1
y
1
y
2
❐ 入力層が１００、中間層が２、出力層が１０の場合 求める重み（辺の太さ）の数は 100 * 2 * 10 = 2000
❐ w1とw2の辺の太さを-10から10まで、２０通り調べるとすると、パラメータ試行回数Nは
N= (100*20) * (2*20) * (10*20) = 16000000
❐パラメータの幅（辺の太さ）をW、３層の多層パーセプトロンとすると、
W＾３*2000のパラメータを試す必要がある。
y1
0
Y軸:N（パラメータ試行回数
X軸:W（パラメータの幅）
総あたり法や、方程式を解く方法は
不可能

6. 勾配降下法① – 1変数(１つの重み）
①現地点Wでの勾配を計算する
ことにより方向を特定
②誤差の小さくなる方向に
Wを変化させる
❐ 重みを変化させると誤差が変化する
❐ 勾配は𝛻𝐸とする
❐ 誤差Eが最小になるような重みの値を見つける
❐ 勾配を使った反復学習により、パラメータを逐次的に更新することで最適解を探索するアプローチ。
① 現時点Wでの勾配を計算する
② 誤差の小さくなる方向へWを変化させる
ΔE = * ΔW
Δ ΔW
Δ
Δw = (Δ𝑤 , Δ𝑤 , … Δ𝑤 )

7. 勾配降下法② - ２変数(2つの重み）
ΔError=h(w1, w2)
w1=0, w2=0の時
Errorの値が最小(0)
等高線 (Eが標高）
ΔE = ▽E * ΔW
<0 (0以下)の値を
取るときに誤差は
確実に減少方向に
進む。
計算したら出てく
る値であり、変更
できない。
変更できるのは
この値。
最小値（E=０）
等高線: Eが同じ値になる
w1とw2の組み合わせを線に
したもの。
等高線が近接していればいる
ほど、局面の傾きが急になる。
最も誤差が急になるのは常に
等高線に対して垂直な方向。
❐ ΔError=h(w1, w2)として、２次元の曲面を下っていくイメージで考える。

8. リバースモード自動微分①（重みの更新）
誤差E
（連鎖率）
動的計画法
b1
入力x 出力u 出力y
入力層(x) 中間層(u) 出力層
(y)
教師信号t
誤差E
b2
重みW1 重みW2
多層パーセプトロンの重みの更新には、勾配降下法と自動微分を使う
① 連鎖率を使って勾配を計算
② 勾配によって重みを更新
教師信号（目的変数）
❐ η：学習係数
勾配によってどれだけ重みを
変化させるかの度合いを示す

9. リバースモード自動微分②（勾配の計算）
E = y
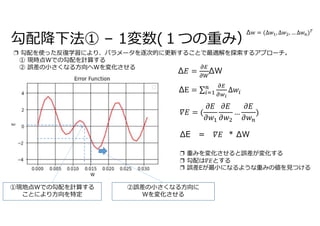
勾配
加重総和関数の微分
損失関数の微分
=
活性関数の微分
∑
x[j]
w[j][k]
u[k] y[k]
重みの更新式
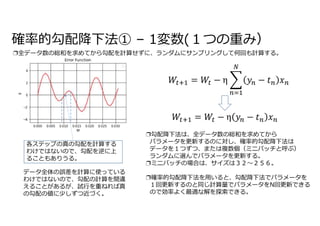
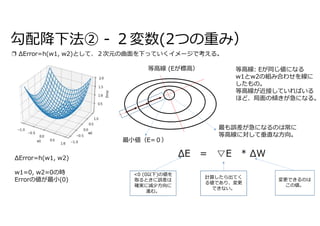
勾配𝛻𝐸は、損失関数、活性関数、加重総和関数をそれぞれ偏微分をしたものをまとめたものになる。

10. 勾配降下法の２つの問題点
❐ データサイズの問題
すべてのデータに対する平均誤差の勾配を計算すると
非常に莫大な計算量になってしまう。
サイズNが大きくなると、データをオンメモリに乗せ
る容量が足りない、または計算量が莫大になるという
問題が生じる。
❐ ローカルミニマム（極小値）に陥る問題
全てのデータに対して勾配を計算する場合、一回計算
した勾配がパラメータの移動方向を決定してしまうた
め、微小値を動かすという勾配降下法の観点から、一
度ローカルミニマムに陥ったら抜け出せなくなる。
極小値
（ローカルミニマム）
大域的最小値
（グローバルミニマム）
学習率
W軸方向の
ステップの
大きさ

11. 確率的勾配降下法① – 1変数(１つの重み）
各ステップの真の勾配を計算する
わけではないので、勾配を逆に上
ることもありうる。
❐勾配降下法は、全データ数の総和を求めてから
パラメータを更新するのに対し、確率的勾配降下法は
データを１つずつ、または複数個（ミニバッチと呼ぶ）
ランダムに選んでパラメータを更新する。
❐ミニバッチの場合は、サイズは３２～２５６。
❐確率的勾配降下法を用いると、勾配降下法でパラメータを
１回更新するのと同じ計算量でパラメータをN回更新できる
ので効率よく最適な解を探索できる。
データ全体の誤差を計算に使っている
わけではないので、勾配の計算を間違
えることがあるが、試行を重ねれば真
の勾配の値に少しずつ近づく。
❐全データ数の総和を求めてから勾配を計算せずに、ランダムにサンプリングして何回も計算する。

12. 勾配降下法 確率的勾配降下法
❐（通常の）勾配降下法は、データ全体を使うので、一直線に最小値に向かうイメージ
❐（ミニバッチ）確率的勾配法は、谷をジグザグに下るイメージ
❐ （ミニバッチ）確率的勾配法は、全体の誤差Eを最小化するわけではない。少し横にずれて移動していく。
そのため、（特にランダムにバッチを選択した場合）偶然、極小値から外れることができる場合が期待できる。
確率的勾配降下法② - ２変数(2つの重み）
方向が同じ
方向が異なる
最小値（E=０） 最小値（E=０）
❐ ΔError=h(w1, w2)として、２次元の曲面を下っていくイメージで考える。
w2
w1
w2
w1

13. Pythonによる実装（モジュール化）
重みW 層（データ変換）
出力（予測値）Y 真の目的値（教師信号）t
損失関数
誤差E
最適化関数
入力X
入力層 中間層 出力層 教師信号t
X U Y
E
確率的勾配降下法は、
最適化関数として
ここにモジュール化される。
深層学習のソフトウェアスタック

14. 誤差逆伝播 まとめ
❐ 多層パーセプトロンを学習させる方法
❐ すべてのディープラーニングのモデルにおいて必要となる手法
以下のアルゴリズムによって構成される。
❐勾配降下法
❐リバースモード自動微分
❐確率的勾配降下法
❐モジュール化による実装