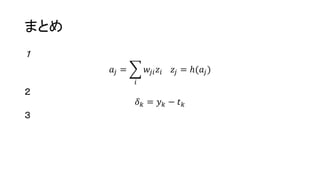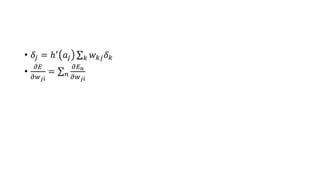More Related Content
PDF
PPTX
DOC
PDF
Jan Chatan CV (Office Administrator) PPT
14 расширенные возможности корпоративных субд PPTX
PDF
Good Transboundary Water Governance PPTX
CĂN HỘ CAO CẤP, DỊCH VỊ CHO THUÊ KINH DOANH EVERICH INFINITY-QUẬN 5.HOTLINE C... Viewers also liked
DOCX
Kehidupan anak kos tugas AGAMA ISLAM PDF
Puntos notables de un triángulo PDF
Natural color serving tray PDF
Brandnew(s) magazine juni 2016 PPTX
PPT
10 компонентные и офисные приложения на платформе microsoft PDF
DOCX
PPT
PDF
Actividades de triángulos Similar to Prml5
PPTX
PDF
PDF
PPTX
PDF
PRML 5.2.1-5.3.3 ニューラルネットワークの学習 (誤差逆伝播) / Training Neural Networks (Backpropa... PDF
PDF
PPTX
PPTX
PDF
PRML上巻勉強会 at 東京大学 資料 第5章5.1 〜 5.3.1 PDF
PPTX
PDF
PDF
PDF
PDF
Casual learning machine learning with_excel_no6 PDF
PDF
東京都市大学 データ解析入門 7 回帰分析とモデル選択 2 PDF
PDF
Prml5
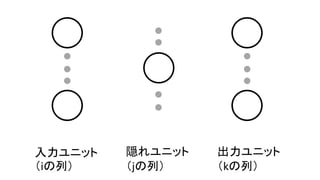
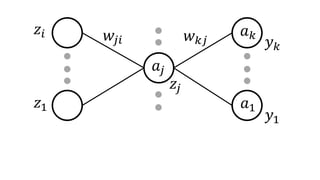
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
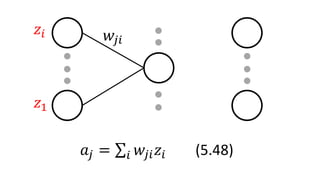
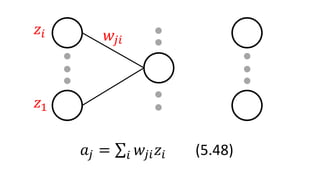
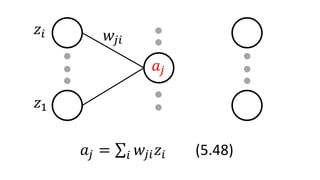
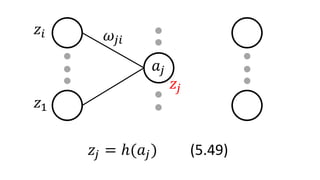
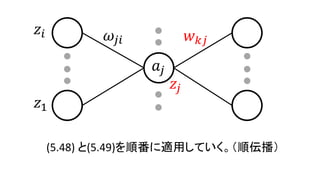
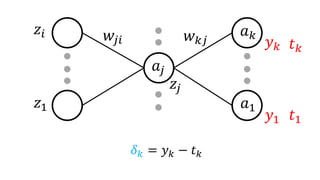
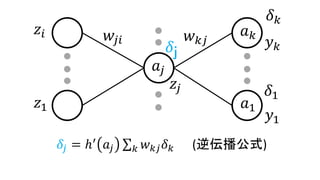
𝑎𝑗 = 𝑖𝑤𝑗𝑖 𝑧𝑖 (5.48)
𝑧𝑖
𝑧1
𝑤𝑗𝑖
𝑎𝑗
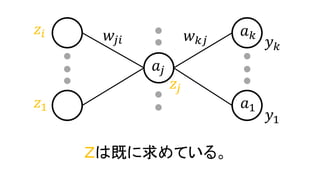
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
•
𝜕𝐸 𝑛
𝜕𝑤 𝑗𝑖
=
𝜕𝐸𝑛
𝜕𝑎 𝑗
𝜕𝑎 𝑗
𝜕𝑤 𝑗𝑖
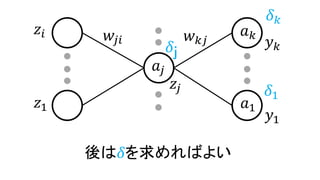
• 𝛿𝑗 ≡
𝜕𝐸 𝑛
𝜕𝑎 𝑗
•
𝜕𝑎 𝑗
𝜕𝑤 𝑗𝑖
= 𝑧𝑖
•
𝜕𝐸 𝑛
𝜕𝑤 𝑗𝑖
= 𝛿𝑗 𝑧𝑖
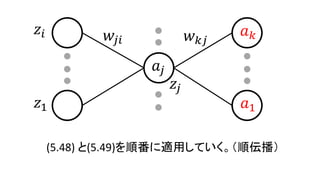
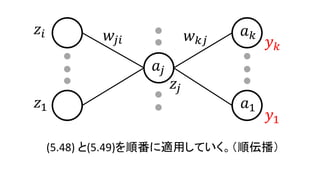
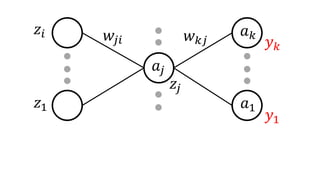
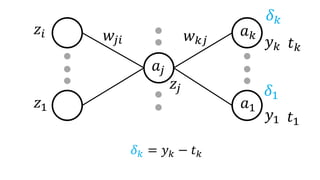
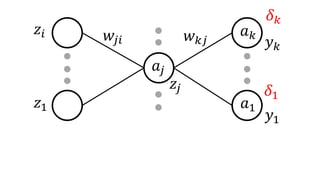
• 𝛿 𝑘 = 𝑦 𝑘 − 𝑡 𝑘
• 𝛿𝑗 ≡
𝜕𝐸 𝑛
𝜕𝑎 𝑗
= 𝑘
𝜕𝐸 𝑛
𝜕𝑎 𝑘
𝜕𝑎 𝑘
𝜕𝑎 𝑗
- 33.
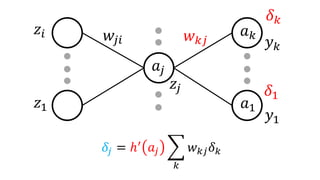
• 𝛿𝑗 =ℎ′
𝑎𝑗 𝑘 𝑤 𝑘𝑗 𝛿 𝑘
•
𝜕𝐸
𝜕𝑤 𝑗𝑖
= 𝑛
𝜕𝐸 𝑛
𝜕𝑤 𝑗𝑖