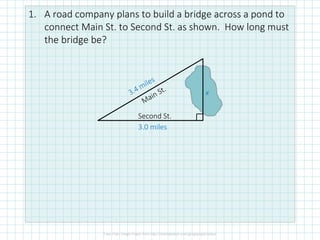
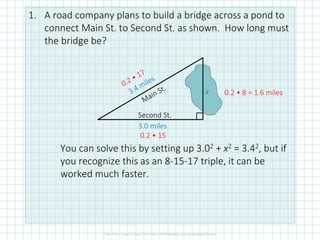
This document discusses using the Pythagorean theorem to solve problems. It provides three examples of applying the theorem: (1) calculating the length of a bridge between two streets, (2) finding the height of a tree branch break from where the top of the tree fell, and (3) determining how long lights need to be to reach the ground from the top of an oil derrick. The document emphasizes setting up the problems correctly and checking answers are realistic.

1. Pythagorean Theorem Problems
Objectives
• Practice using the Pythagorean Theorem to solve
problems

2. • What we now call the Pythagorean Theorem was first
developed thousands of years ago empirically, which
means that it was based on observations of data.
• One of the well-known ancient uses of the relationship
between the sides of right triangles was in Egypt by the
Pharoah’s tax assessors to determine property
boundaries.
• With this in mind, let’s look as some examples of using the
Pythagorean Theorem to solve problems.

3. 1. A road company plans to build a bridge across a pond to
connect Main St. to Second St. as shown. How long must
the bridge be?
Second St.
3.0 miles
x

4. 1. A road company plans to build a bridge across a pond to
connect Main St. to Second St. as shown. How long must
the bridge be?
You can solve this by setting up 3.02 + x2 = 3.42, but if
you recognize this as an 8-15-17 triple, it can be
worked much faster.
Second St.
3.0 miles
x

5. 1. A road company plans to build a bridge across a pond to
connect Main St. to Second St. as shown. How long must
the bridge be?
You can solve this by setting up 3.02 + x2 = 3.42, but if
you recognize this as an 8-15-17 triple, it can be
worked much faster.
Second St.
3.0 miles
x
0.2 • 15
0.2 • 8 = 1.6 miles

6. 2. A wind storm caused the top of a 25 ft tree to crack, and
the top fell to the ground but not break off. If the top of
the tree hit the ground 8 ft from the trunk, how far above
the ground was the break?

7. 2. A wind storm caused the top of a 25 ft tree to crack, and
the top fell to the ground but not break off. If the top of
the tree hit the ground 12 ft from the trunk, how far
above the ground was the break?
The tricky part of this
problem is the set up.
We know the tree is 25
ft tall, so we let the
break be x.
We can then let the hypotenuse (the rest of the tree)
be 25 – x. The third side of the triangle is the 12 ft.
x
12

8. 2. A wind storm caused the top of a 25 ft tree to crack, and
the top fell to the ground but not break off. If the top of
the tree hit the ground 12 ft from the trunk, how far
above the ground was the break?
x
12
( )
2
2 2
2 2
12 25
144 625 50
481 50
9.62 ft
x x
x x x
x
x
+ = −
+ = − +
− = −
=

9. 3. Six Flags is stringing lights from the observation deck of
the oil derrick to the ground to form a Christmas tree. If
the platform is 300 ft above the ground, and the lights
will touch the ground 75 ft from the base of the tower,
how long must each strand of lights be?
75 ft
300 ft x

10. 3. Six Flags is stringing lights from the observation deck of
the oil derrick to the ground to form a Christmas tree. If
the platform is 300 ft above the ground, and the lights
will touch the ground 75 ft from the base of the tower,
how long must each strand of lights be?
75 ft
300 ft x
2 2 2
2
75 300
95625
95625 309.2 ft
x
x
x
= +
=
= 

11. One final note: Most problems you will be working
on should have somewhat realistic data. Keep that in
mind when you get your answer.
1. Remember the hypotenuse has to be the longest
side of the triangle.
2. One of the most common mistakes is forgetting
to take the square root after you’ve solved for x2.
If you end up with an outrageously large answer,
that would be the first thing to check.