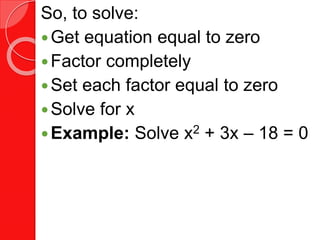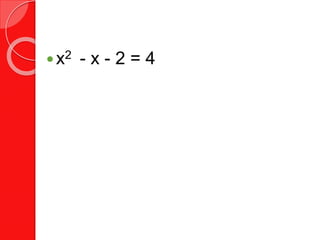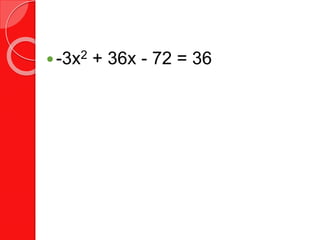This document provides instruction on solving quadratic equations by factoring. It begins by explaining what factoring is and how to factor trinomials of the form x^2 + bx + c. Examples are given of factoring different types of trinomials, including those where b is negative or c is negative. The document then explains how to use the zero product property to solve quadratic equations after factoring them into binomial form. Several examples of solving equations by factoring are shown. Finally, applications of factoring quadratic equations to area word problems are presented.

1. 6.3 Solving
Quadratic Equations
by Factoring

2. What is Factoring?
Used to write trinomials as a
product of binomials.
Works like FOIL in reverse.
Example: Multiply (x + 2)(x + 7)
What do you notice about the 2
and 7?

3. Factoring x2 + bx + c
 x2 + bx + c = (x + m)(x + n)
Need to find m and n so
m+n = b and m·n = c
First, find all factor pairs of c.
Find their sums.
Choose the pair whose sum
equals b.

4. Example:
Factor x2 + 5x + 6
Multiply (FOIL) to check your
answers!
Factor
Pairs
Sum

5. Example:
Factor x2 + 13x + 40 Factor
Pairs
Sum

6. You Try!
Factor x2 + 9x + 14

7. More Factoring
What if b is negative and c is
positive?
For example: x2 - 7x + 10
◦ Choose negative factors!

8. You Try!
Factor x2 - 4x + 3

9. What if?
What if c is negative?
For example: x2 - 8x – 20
◦ Choose one positive and one
negative!

10. Example:
Factor x2 + 3x – 10

11. You Try!
Factor x2 - 2x – 48

12. Factoring Out
Monomials
Check if you can factor out
something from each term.
Example: Factor 5x2 – 15x – 20

13. Example:
Factor 2x2 + 8x

14. You Try!
Factor:
6x2 + 15x 4x2 - 20x +24

15. Solving by Factoring
Some quadratic equations can
be solved by factoring.
Standard form: ax2 + bx + c = 0
Zero Product Property:
◦ If A x B = 0, then A = 0 or B = 0.

16. So, to solve:
Get equation equal to zero
Factor completely
Set each factor equal to zero
Solve for x
Example: Solve x2 + 3x – 18 = 0

17. Examples:
Solve by factoring.
x2 - 3x – 4 = 0

18. x2 - x - 2 = 4

19. You Try!
Solve by factoring.
x2 + 19x + 88 = 0

20. Examples:
Solve by factoring:
2x2 + 8x – 64 = 0

21. -3x2 + 36x - 72 = 36

22. You Try!
Solve by factoring.
-4x2 - 4x + 48 = 0

23. Applications –
Area Problems
1. Draw a picture!
2. Write an equation.
3. Get eqn. into standard form.
4. Factor.
5. Solve.
6. Answer the question with a
SENTENCE.

24. Example 1:
 A square field had 5m added to its
length and 2m added to its width.
The new area is 150m2. Find the
length of a side of the original
square.
x
x
+5
+2

26. Example 2:
 A rectangular garden is 3m long by
10m wide. You want to increase the
length and the width by the same
amount to double the area. Find
the dimensions of the new garden.
10
3
+ x
+ x

28. You Try!
 A rectangular garden is 4m long by
5m wide. Each dimension is
increased by the same amount.
The new area is 56m2. Find the
dimensions of the new garden.