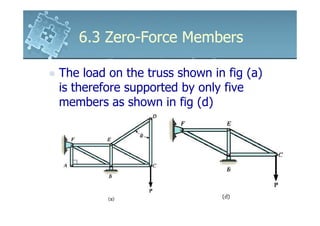
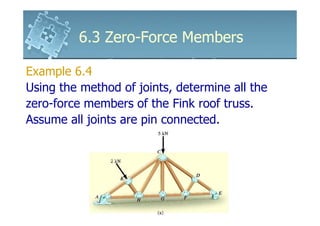
Zero-force members are truss members that do not experience any internal forces from applied loads. They are used to increase stability during construction and allow the truss to support changed loadings. By examining the force and moment equilibrium at joints, members that are determined to have zero force can be identified. If two members meet at a joint with no external loads or supports, those members must be zero-force members. Similarly, if three members meet collinearly at a joint with no external loads, the third member is a zero-force member.

1. 6.3 Zero-Force Members
Method of joints is simplified when the
members which support no loading are
determined
Zero-force members (support no loading )
are used to increase the stability of the
truss during construction
and to provide support
if the applied loading is
changed

2. 6.3 Zero-Force Members
Consider the truss shown
From the FBD of the pin at point A,
members AB and AF become
zero force members
*Note: Consider the FBD of
joints F or B, there are
five unknowns and the
above conclusion
would not be reached

3. 6.3 Zero-Force Members
Consider FBD of joint D
DC and DE are zero-force members
As a general rule, if only two members
form a truss joint and no external load or
support reaction is
applied to the joint, the
members must be
zero-force members

4. 6.3 Zero-Force Members
The load on the truss shown in fig (a)
is therefore supported by only five
members as shown in fig (d)

5. 6.3 Zero-Force Members
Consider the truss shown
From the FBD of the pin of the joint D, DA
is a zero-force member
From the FBD of the pin of the joint C, CA
is a zero-force member

6. 6.3 Zero-Force Members
In general, if three members form a truss
joint for which two of the members are
collinear, the third member is a zero-force
member provided no
external force or support
reaction is applied to the joint
The truss shown is
suitable for
supporting the load P

7. 6.3 Zero-Force Members
Example 6.4
Using the method of joints, determine all the
zero-force members of the Fink roof truss.
Assume all joints are pin connected.

8. 6.3 Zero-Force Members
Solution
Joint G
+ ↑ ∑ Fy = 0; FGC = 0
GC is a zero-force member
meaning the 5kN load at C
must be supported by CB, CH, CF and CD
Joint D
∑ Fx = 0; FDF = 0

9. 6.3 Zero-Force Members
Solution
Joint F
+ ↑ ∑ Fy = 0; FFC cos θ = 0
θ ≠ 90o , FFC = 0
Joint B
∑ Fx = 0;2kN − FBH = 0
FBH = 2kN (C )

10. 6.3 Zero-Force Members
Solution
FHC satisfy ∑Fy = 0 and therefore HC is not a
zero-force member