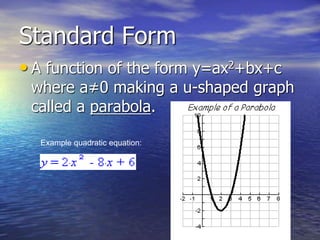
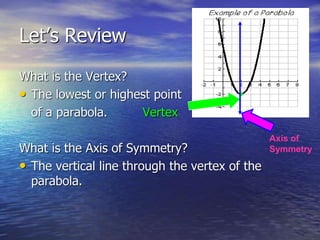
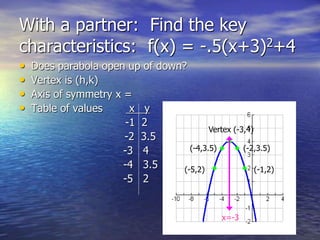
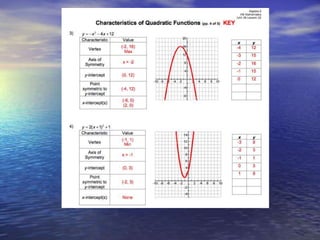
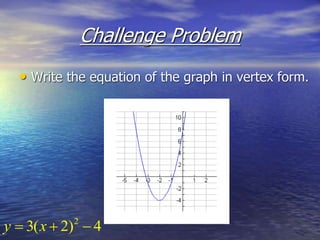
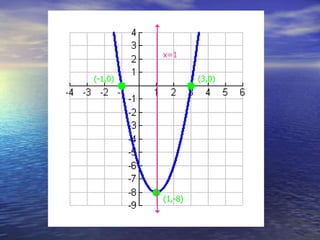
The document discusses the factoring and graphing of quadratic functions, highlighting their vertex form and important characteristics like the vertex and axis of symmetry. It provides examples of quadratic equations and illustrates how to graph them by plotting the vertex and utilizing symmetry. Additionally, it explains the process of converting between standard and vertex forms of quadratic equations.

1. Do Now
1. Factor: f(x) = 3x2 + 10x + 8
2. Factor f(x) = 2x2 - 7x + 3

2. Today’s Question:
Today’s Question:
How do you graph quadratic
functions in vertex form?
What important characteristics do
you see in the vertex form?

3. Standard Form
• A function of the form y=ax2+bx+c
where a≠0 making a u-shaped graph
called a parabola.
Example quadratic equation:

4. Let’s Review
What is the Vertex?
• The lowest or highest point
of a parabola. Vertex
What is the Axis of Symmetry?
• The vertical line through the vertex of the
parabola.
Axis of
Symmetry

5. Vertex Form Equation
y=a(x-h)2+k
• If a is positive, parabola opens up
If a is negative, parabola opens down.
• The vertex is the point (h,k).
• The axis of symmetry is the vertical line
x=h.
• Don’t forget about 2 points on either side
of the vertex! (5 points total!)

6. Vertex Form
Every function can be written in the form (x – h)2 + k,
where (h , k) is the vertex of the parabola, and x = h
is its axis of symmetry.
(x – h)2 + k – vertex form
Equation Vertex Axis of Symmetry
y = x2 or
y = (x – 0)2 + 0
(0 , 0) x = 0
y = x2 + 2 or
y = (x – 0)2 + 2
(0 , 2) x = 0
y = (x – 3)2 or
y = (x – 3)2 + 0
(3 , 0) x = 3

7. Example 1: Graph y = (x + 2)2 + 1
•Analyze y = (x + 2)2 + 1.
• Step 1 Plot the vertex (-2 , 1)
• Step 2 Draw the axis of symmetry, x = -2.
• Step 3 Find and plot two points on one side
, such as (-1, 2) and (0 , 5).
• Step 4 Use symmetry to complete the graph,
or find two points on the
• left side of the vertex.

8. With a partner: Find the key
characteristics: f(x) = -.5(x+3)2+4
• Does parabola open up of down?
• Vertex is (h,k)
• Axis of symmetry x =
• Table of values x y
-1 2
-2 3.5
-3 4
-4 3.5
-5 2
Vertex (-3,4)
(-4,3.5)
(-5,2)
(-2,3.5)
(-1,2)
x=-3

9. Now you try one!

11. Changing from vertex or intercepts
form to standard form
• The key is to FOIL! (first, outside, inside,
last)
• Ex: y=-(x+4)(x-9) Ex: y=3(x-1)2+8
=-(x2-9x+4x-36) =3(x-1)(x-1)+8
=-(x2-5x-36) =3(x2-x-x+1)+8
y=-x2+5x+36 =3(x2-2x+1)+8
=3x2-6x+3+8
y=3x2-6x+11

12. Converting from standard to vertex fom
http://www.virtualnerd.com/
algebra-2/quadratics/solve-
by-completing-square-
roots/complete-
square/completing-square-
convert-standard-to-vertex

13. Challenge Problem
• Write the equation of the graph in vertex form.
2
3( 2) 4
y x
  

14. (-1,0) (3,0)
(1,-8)
x=1