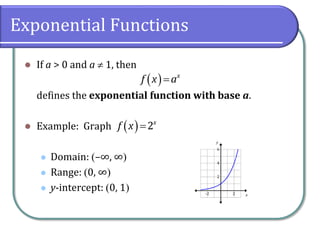
This document provides an overview of exponential functions and their properties. It begins by defining exponential functions with a base a as f(x)=ax and discussing their key characteristics. It then covers solving exponential equations by setting exponents equal and using properties of exponents. Applications discussed include compound interest formulas where interest is compounded n times per year or continuously. Examples solve various compound interest and exponential equation problems. The document concludes with assigning practice problems from the textbook.

1. Exponential Functions
Chapter 4 Inverse, Exponential, and Logarithmic
Functions

2. Concepts & Objectives
 Exponential Functions
 Use exponent properties to solve equations
 Substitute values into exponential functions

3. Properties of Exponents
 Recall that for a variable x and integers a and b:

 
a b a b
x x x


a
a b
b
x
x
x
  
b
a ab
x x
 b
a b a
x x
  
a b
x x a b

4. Simplifying Exponents
 Example: Simplify
 1.
 2.
 3.

3 2 2
2 5
25
5
x y z
xy z
 
 4
2 3
2r s t


2 3 1 2
5 6
y y

5. Simplifying Exponents
 Example: Simplify
 1.
 2.
 3.

3 2 2
2 5
25
5
x y z
xy z
 
 4
2 3
2r s t


2 3 1 2
5 6
y y
   
 3 1 2 2 2 5
5x y z
   

 4 2 4 3
4 4
2 r s t
  


2 1
3 2
5 6 y
 
 2 4 3
5x y z

 8 12 4
16r s t

1
6
30y

6. Exponential Functions
 If a > 0 and a  1, then
defines the exponential function with base a.
 Example: Graph
 Domain: –∞, ∞
 Range: 0, ∞
 y-intercept: 0, 1
  x
f x a
 2x
f x

7. Exponential Functions (cont.)
Characteristics of the graph of :
1. The points are on the graph.
2. If a > 1, then f is an increasing function; if 0 < a < 1, then
f is a decreasing function.
3. The x-axis is a horizontal asymptote.
4. The domain is –∞, ∞, and the range is 0, ∞.
  x
f x a
   
 

 
 
1
1, , 0,1 , 1,a
a

8. Exponential Equations
 Exponential equations are equations with variables as
exponents.
 If you can re-write each side of the equation using a
common base, then you can set the exponents equal to
each other and solve for the variable.
 Example: Solve 
1
5
125
x

 3
5 5
x
3
x
 3
125 5

9. Exponential Equations (cont.)
 Example: Solve  

1 3
3 9
x x

10. Exponential Equations (cont.)
 Example: Solve  

1 3
3 9
x x
 2
9 3
 



3
1 2
3 3
x
x
 
  
1 2 3
x x
  
1 2 6
x x

7 x
 


 2 3
1
3 3 x
x

11. Exponential Equations (cont.)
 To solve an equation with exponents, you can “undo” the
exponent by raising each side to the reciprocal.
 Solve 
5 2
243
b

12. Exponential Equations (cont.)
 To solve an equation with exponents, you can “undo” the
exponent by raising each side to the reciprocal.
 Solve 
5 2
243
b
   

2
2
5 5
5
2
243
b
9
b

13. Compound Interest
 The formula for compound interest (interest paid on
both principal and interest) is an important application
of exponential functions.
 Recall that the formula for simple interest, I = Prt, where
P is principal (amount deposited), r is annual rate of
interest, and t is time in years.

14. Compound Interest (cont.)
 Now, suppose we deposit $1000 at 10% annual interest.
At the end of the first year, we have
so our account now has 1000 + .11000 = $1100.
 At the end of the second year, we have
so our account now has 1100 + .11100 = $1210.
  
 
1000 0.1 100
I
  
 
1100 .1 110
I

15. Compound Interest (cont.)
 Another way to write 1000 + .11000 is
 After the second year, this gives us
   
 
  
1000 1 .1 .1 1000 1 .1   
  
1000 1 .1 1 .1
 
 
2
1000 1 .1
 

1000 1 .1

16. Compound Interest (cont.)
 If we continue, we end up with
This leads us to the general formula.
Year Account
1 $1100 10001 + .1
2 $1210 10001 + .12
3 $1331 10001 + .13
4 $1464.10 10001 + .14
t 10001 + .1t

17. Compound Interest Formulas
 For interest compounded n times per year:
 For interest compounded continuously:
where e is the irrational constant 2.718281…
 
 
 
 
1
tn
r
A P
n
 rt
A Pe

18. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?

19. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A P = 2500, r = .06,
n = 2, t = 10

20. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A

21. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A = $4515.28

22. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A
 
 
 
 
 
4 8
.048
15000 1
4
P A = 15000, r = .048,
n = 4, t = 8
= $4515.28

23. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A
 
 
 
 
 
4 8
.048
15000 1
4
P
 

15000 1.4648
P
= $4515.28

24. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A
 
 
 
 
 
4 8
.048
15000 1
4
P
 

15000 1.4648
P
= $4515.28

25. Examples
1. If $2500 is deposited in an account paying 6% per year
compounded twice per year, how much is the account
worth after 10 years with no withdrawals?
2. What amount deposited today at 4.8% compounded
quarterly will give $15,000 in 8 years?
 
 
 
 
 
2 10
.06
2500 1
2
A
 
 
 
 
 
4 8
.048
15000 1
4
P
 

15000 1.4648
P
$10,240.35
P
= $4515.28

26. Examples
3. If $8000 is deposited in an account paying 5% interest
compounded continuously, how much is the account
worth at the end of 6 years?
4. Which is a better deal, depositing $7000 at 6.25%
compounded every month for 5 years or 5.75%
compounded continuously for 6 years?

27. Examples
3. If $8000 is deposited in an account paying 5% interest
compounded continuously, how much is the account
worth at the end of 6 years?
4. Which is a better deal, depositing $7000 at 6.25%
compounded every month for 5 years or 5.75%
compounded continuously for 6 years?
  
 .05 6
8000
A e
$10,798.87
A
 
 
 
 
 

12 5
.0625
7000 1
12
$9560.11
A
  


.0575 6
7000
$9883.93
A e

28. Classwork
 4.2 Assignment (College Algebra)
 Page 429: 50-68 (even), page 413: 52-66 (even),
page 385: 32-42 (even)
 4.2 Classwork Check
 Quiz 4.1