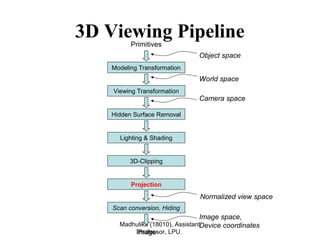
This document discusses different types of projections used in 3D viewing pipelines, including perspective and parallel projections. Perspective projections use a center of projection to project 3D points onto a 2D view plane, resulting in effects like foreshortening and vanishing points. Parallel projections project points parallel to a viewing direction, preserving scale and shape. Specific types of parallel projections discussed include orthographic, oblique, isometric, and axonometric projections.