Downloaded 14 times
![事後分布の評価
事前知識
無作為に選んだ10人に、現在国会審議中のある法案に賛成か否かどう
か質問したところ８人が賛成しました。標本比率は0.8(=8/10)です。しか
し、別の10人、さらに別の10人、さらに更に調査することを考えます。標
本比率は調査のたびに違った値になり、それは分布を構成します。この
ような分布を標本比率の標本分布という。
標本分布・・・データから計算される数的指標の分布
母比率E[X] の母集団からｎ人の標本を抽出した場合、
標本分布の平均はE[X]
分散はV[E]=E[x](1-[E])/n
母比率の代わりに標本比率を使って計算すると、V[E]=0.016、r=9
標本比率の標本分布はp=7.2、q=1.8のベータ分布で近似可能](https://image.slidesharecdn.com/33-170522025842/85/3-3-1-3-3-17-320.jpg)
![[DL輪読会]Bayesian Uncertainty Estimation for Batch Normalized Deep Networks](https://cdn.slidesharecdn.com/ss_thumbnails/190719dlver2-190719035734-thumbnail.jpg?width=640&height=640&fit=bounds)
![[PRML] パターン認識と機械学習（第2章：確率分布）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter2-171002030018-thumbnail.jpg?width=640&height=640&fit=bounds)
基礎からのベイズ統計学 3章（3.1～3.3）
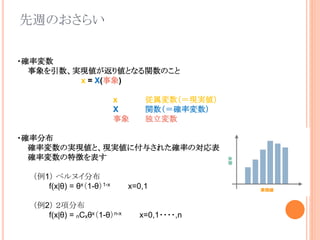
- 1.
- 2. 第３章の目的 確率に関する「ベイズの定理」 第１章 分布に関する「ベイズの定理」 第３章 拡張
- 3. 先週のおさらい ・確率変数 事象を引数、実現値が返り値となる関数のこと x = X(事象) x従属変数（＝現実値） X 関数（＝確率変数） 事象 独立変数 ・確率分布 確率変数の実現値と、現実値に付与された確率の対応表 確率変数の特徴を表す （例1） ベルヌイ分布 f(x|θ) = θx（1-θ）1-x x=0,1 （例2） ２項分布 f(x|θ) = nCxθx（1-θ）n-x x=0,1・・・・,n
- 4.
- 5. ところが、 乗法定理のAiをθをみなして、Biをxとみなして書き換えると、立場が決裂 乗法定理 p(Ai, Bi) =p(Bj | Aj) p(Aj) f(θ, x) = f(x |θ) f(θ) p(Ai, Bi) = p(Aj | Bj) p(Bj) f(θ, x) = f(θ|x) f(x) 伝統的な統計学では、上記の変換式を原則許さない 伝統的な統計学・・・母数θは未知だけど固定された非確率変数 ベイズ統計学・・・f(θ)を母数の分布として導入。母数θは確率変数として扱う
- 6. ところが、 乗法定理のAiをθをみなして、Biをxとみなして書き換えると、立場が決裂 乗法定理 p(Ai, Bi) =p(Bj | Aj) p(Aj) f(θ, x) = f(x |θ) f(θ) p(Ai, Bi) = p(Aj | Bj) p(Bj) f(θ, x) = f(θ|x) f(x) 伝統的な統計学では、上記の変換式を原則許さない 伝統的な統計学・・・母数θは道だけど固定された日確率変数 ベイズ統計学・・・f(θ)を母数の分布として導入。母数θは確率変数として扱う ベイズ統計学では、右辺を等式 でつなぎ、両辺をf(x)で割る 𝑓(𝜃|𝑥) = 𝑓 𝑥 𝜃 𝑓(𝜃) 𝑓(𝑥)
- 7. 分布に関するベイズの定理 𝑓(𝜃|𝑥) = 𝑓 𝑥𝜃 𝑓(𝜃) 𝑓(𝑥) 𝑓(𝜃|𝑥)・・・事後確率分布 𝑓(𝑥|𝜃)・・・尤度 𝑓(𝜃)・・・事前確率分布 𝑓(𝑥) = −∞ +∞ 𝑓 𝑥 𝜃 𝑓 𝜃 𝑑𝜃 𝑓(𝜃|𝑥) = 𝑓 𝑥 𝜃 𝑓(𝜃) −∞ +∞ 𝑓 𝑥 𝜃 𝑓 𝜃 𝑑𝜃 全確率の公式
- 8. まとめ ベイズの定理 事前確率が客観確率である場合は、伝統的な統計学者も認 める。 分布に関するベイズの定理 θを確率変数とみるか、非確率変数とみるかによって、出発 点から伝統的な統計学とはたもとを分かつ。 数理的な仮定の問題なので、ベイズ統計学と伝統的統計 学のどちらが正しいかを判断することはできない。 出発点の仮定の違いによって長所・短所がある。それをき ちんと踏まえることが大事。
- 9.
- 10. カーネル 確率分布や尤度において、母数と変数を含んだ部分。 確率分布や尤度の本質的な性質を決定する。 赤部分が２項分布の性質を決める。それを強調するために ２項分布の確率関数を下記のように示すこともある。 𝑓(𝜃|𝑥) = 𝑛 𝐶 𝑥 𝜃 𝑥 1 − 𝜃 𝑛−𝑥 （例）２項分布 カーネル 𝑓(𝜃|𝑥) ∝ 𝜃 𝑥 1 − 𝜃 𝑛−𝑥
- 11. 正規化定数 確率分布の母数＆変数（？）を含まない部分。 確率分布を確率変数で積分したら１になるようにする。 （参考） 𝑓(𝑥|𝑝, 𝑞) = 𝐵 𝑝, 𝑞 −1 𝑥 𝑝−1 1 − 𝑥 𝑞−1 （例）ベータ分布の確率密度関数 カーネル 𝐵 𝑝, 𝑞 = 0 −1 𝑥 𝑝−1 1 − 𝑥 𝑞−1 𝑑𝑥 正規化定数 𝐵 𝑝, 𝑞 の定義 すべての確率分布は、確率変数で積分すると1になるという性質がある ので↓↓↓ 0 1 𝑓(𝑥|𝑝, 𝑞) = 0 1 𝐵 𝑝, 𝑞 −1 𝑥 𝑝−1 1 − 𝑥 𝑞−1 𝑑𝑥 = 𝐵 𝑝, 𝑞 −1 0 1 𝑥 𝑝−1 1 − 𝑥 𝑞−1 𝑑𝑥 = 1
- 12. ベイズの定理では、 データが所与のときの母数の確率分布（事後分布）を導 出する。 確率分布なので、確率変数θで積分すると１になるはず。 尤度と事前分布の積が事後分布のカーネルとなり、この 部分に、母数に関する情報が集約されている。 ベイズの定理による変形は、上式により積分が1である ことが保証されている。なので、正規化定数を無視して、 カーネルだけに注目してもその分布がなんであるかが わかる（そうすることがベイズ流！）。 0 1 𝑓 𝜃 𝑥 𝑑𝜃 = −∞ ∞ 𝑓 𝑥 𝜃 𝑓(𝜃) 𝑓(𝑥) 𝑑𝜃 = 𝑓 𝑥 −1 −∞ ∞ 𝑓 𝑥 𝜃 𝑓 𝜃 𝑑𝜃 = 1 カーネル正規化定数
- 13.
- 14. 自然共役事前分布 以下の例で、伝統的な統計学とベイズ統計学の違いを 考察しよう 伝統的な統計学 客観的なデータにだけ基づいて勝率を推定⇒Bの勝率 4/7 ベイズ統計学の私的分析 監督の主観も判断材料に利用する。普段はAの方がうまい けど、たまたま直前の1試合だけをポカしただけかもしれない。 正選手問題 ある高校のテニス部で、次の大会の正選手を1名だけ決めることになりま した。候補はA,Bの2選手です。ここ数日の正式記録によるとA対Bの戦績 は3勝4敗です。BがAより優勢です。しかし監督は正選手の決定に悩み ました。それ以前の1週間では8勝2敗ぐらいでAが優勢だと思ったからで す。しかしこれは正式記録としては全く残っておらず、あくまでも茫然とし た監督の個人的印象にしかすぎません。監督はAとBのどちらを正選手 に選ぶべきでしょう。
- 15.
- 16. 自然共役事前分布と尤度の組み合わせ 尤度 事前分布事後分布 ベルヌイ分布 ベータ分布 ベータ分布 ２項分布 ベータ分布 ベータ分布 ポアソン分布 ガンマ分布 ガンマ分布 正規分布の平均 正規分布 正規分布 正規分布の分散 逆ガンマ分布 逆ガンマ分布 尤度がベルヌイ分布や２項分布である場合に、ベータ分布を共役事前分布とし て利用すると・・・ ∝ 𝜃 𝑥 1 − 𝜃 𝑛−𝑥 × 𝜃 𝑝−1 1 − 𝜃 𝑞−1 𝑓(𝜃|𝑥) ∝ 𝑓 𝑥 𝜃 𝑓 𝜃 ∝ 𝜃 𝑥+𝑝−1 1 − 𝜃 𝑛−𝑥+𝑞−1 ∝ 𝜃 𝑝−1 1 − 𝜃 𝑞−1
- 17.
- 18. ベータ分布に関する知見 ベータ分布の確率密度関数は、θ=(p,q)として ベータ分布の平均と分散は 母数は平均と分散で表現すると便利 𝑓(𝑥|𝑝, 𝑞) = 𝐵 𝑝, 𝑞 −1 𝑥 𝑝−1 1 − 𝑥 𝑞−1 E 𝑋 = 𝑝 𝑝 + 𝑞 𝑝 = 𝑟𝐸 𝑋 𝑞 = 𝑟 1 − 𝐸 𝑋 𝑟 = 𝐸 𝑋 1 − 𝐸 𝑋 𝑉 𝑋 − 1 V 𝑋 = 𝑝𝑞 𝑝 + 𝑞 2 𝑝 + 𝑞 + 1
- 19.
- 20.
- 21.