(9/23 表紙を微修正)
機械学習の勉強会の資料
ベイズ統計学について
1. イントロダクション
2. 事後分布の要約
3. ベイズ的モデル選択
4. 事前分布
5. 階層ベイズ
6. 経験ベイズ
7. ベイズ的決定理論
教科書: Murphy, Kevin P. "Machine learning: a probabilistic perspective (adaptive computation and machine learning series)." Mit Press. ISBN 621485037 (2012): 15.







![Baysian Statistics Summarizing posterior distribution
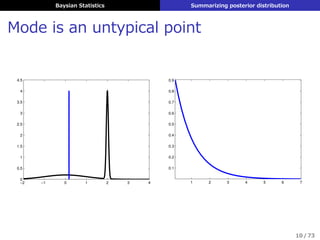
点推定 (point estimate)
θの事後分布 p (θ|D) をある定数ˆθによって表して計算
▶ 平均 (mean)
ˆθ = E [θ] =
ˆ
θp (θ|D) dθ
▶ 中央値 (median) (θが1次元なら)
ˆθ s.t. P
(
θ ≤ ˆθ|D
)
= P
(
θ > ˆθ|D
)
= 0.5
▶ 最頻値 (mode) → MAP推定で求めてるのはこれ
ˆθ = argmax
θ
p (θ|D)
8 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-8-320.jpg)




























![Baysian Statistics Prior
ジェフリーズ事前分布 (Jeffreys prior)
▶ フッシャー情報量の平⽅根に⽐例する事前分布
pϕ (ϕ) ∝ (I (ϕ))1/2
I (ϕ) ≜ −E
[(
d log p (X|ϕ)
dϕ
)2
]1/2
▶ パラメータ変換に対する不変性
θ = h (ϕ), pθ (θ) : Jeffreys ⇒ pϕ (ϕ)
dϕ
dθ
: Jeffreys
44 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-47-320.jpg)








![Baysian Statistics Empirical Bayes
経験ベイズ法 (EB; empirical Bayes)
▶ 階層モデルのハイパーパラメータの事後分布を
点推定で近似
p (η|D) =
ˆ
p (η, θ|D) dθ
≈ δˆη (η)
▶ ˆη = argmax p (η|D)
▶ η の事前分布を⼀様とする (⇒ p (η|D) ∝ p (D|η)) と
ˆη = argmax p (D|η)
= argmax
[ˆ
p (D|θ) p (θ|η) dθ
]
▶ 第2種の最尤推定 (type-II maximum likelihood)
とも呼ぶ (周辺尤度を最⼤化している)
54 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-57-320.jpg)




![Baysian Statistics Bayesian decision theory
▶ 期待効⽤最⼤化原理
(maximum expected utility principle)
δ (x) = argmax
a∈A
E [U (y, a)]
= argmin
a∈A
E [L (y, a)]
▶ 事後期待損失 (posterior expected loss)
ρ (a|x) ≜ Ep(y|x) [L (y, a)] =
∑
y
L (y, a) p (y|x)
▶ ベイズ推定量 (Bayes estimator)
またはベイズ決定則 (Bayes decision rule)
δ (x) = argmin
a∈A
ρ (a|x)
59 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-62-320.jpg)



![Baysian Statistics Bayesian decision theory
⼆乗損失のベイズ推定量
▶ L (y, a) = (y − a)2
▶ 回帰問題で使う
▶ 事後期待損失は
ρ (a|x) = E
[
(y − a)2
|x
]
= E
[
y2
|a
]
− 2aE [y|x] + a2
▶ ベイズ推定量は事後分布の平均
ˆy = E [y|x] =
ˆ
yp (y|x) dy
▶ 最⼩平均⼆乗誤差推定 (minimum mean squared
error; MMSE) とよぶ
63 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-67-320.jpg)

![Baysian Statistics Bayesian decision theory
教師あり学習
真の値yに対する予測y′
についての cost function ℓ (y, y′
)
が与えられたとき,
汎化誤差 (generalization error)
L (θ, δ) ≜ E(x,y)∼p(x,y|θ) [ℓ (y, δ (x))]
=
∑
x
∑
y
L (y, δ (x)) p (x, y|θ)
の事後期待損失
ρ (δ|D) =
ˆ
p (θ|D) L (θ, δ) dθ
を最⼩化する決定⼿順 δ : X → Y を求める
65 / 73](https://image.slidesharecdn.com/mlappch5-150801090752-lva1-app6891/85/MLaPP-5-69-320.jpg)