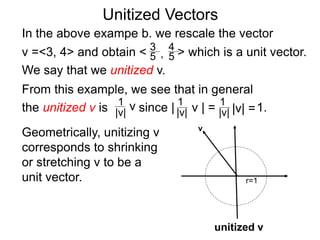
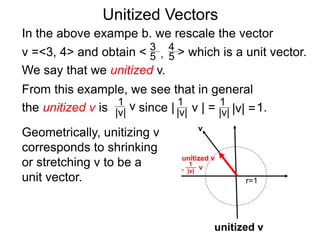
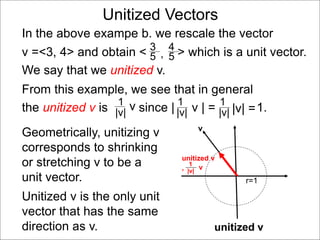
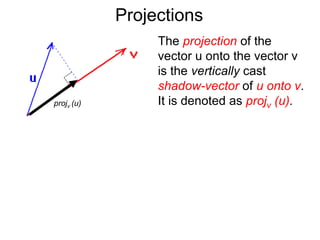
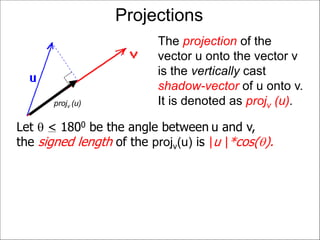
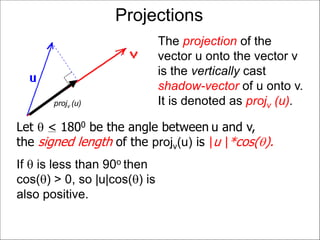
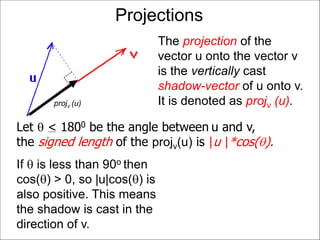
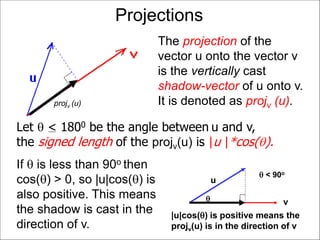
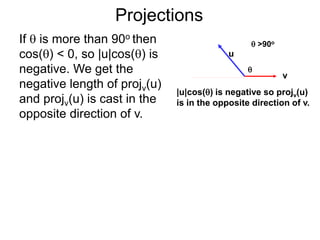
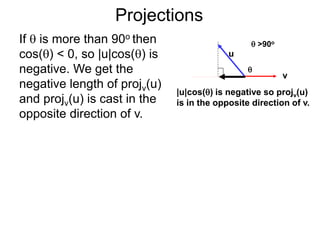
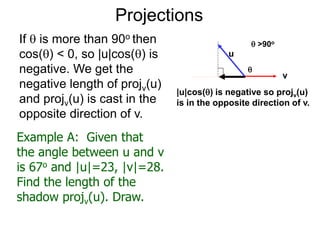
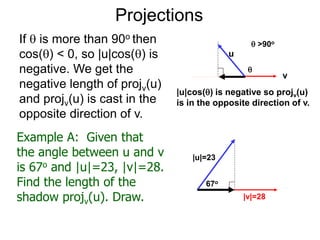
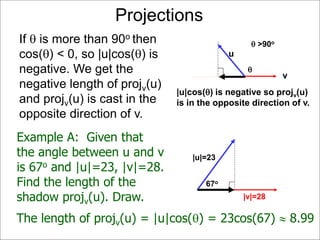
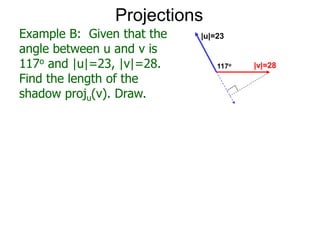
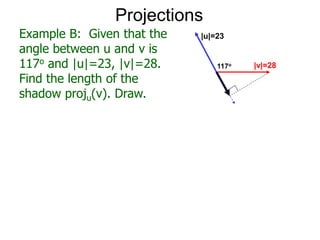
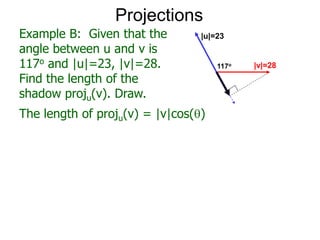
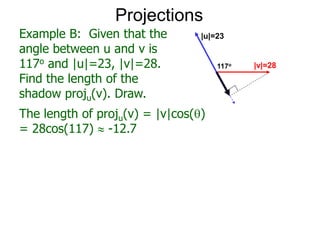
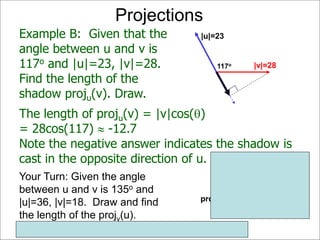
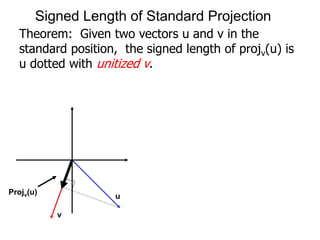
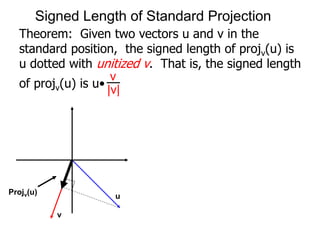
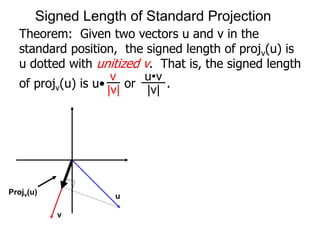
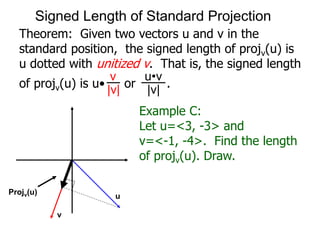
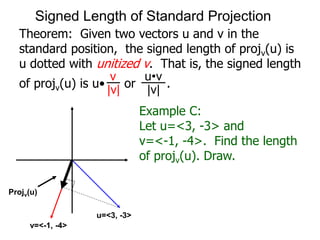
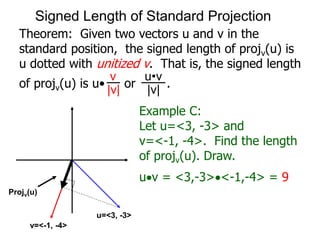
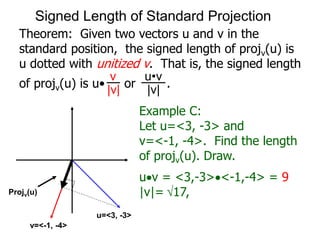
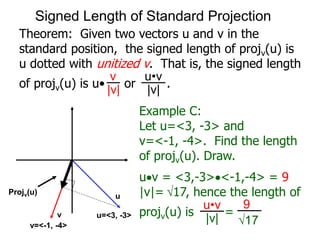
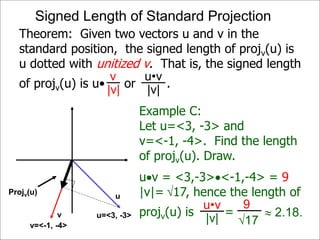
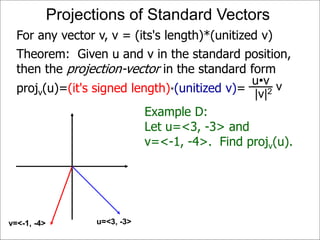
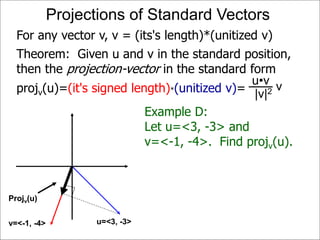
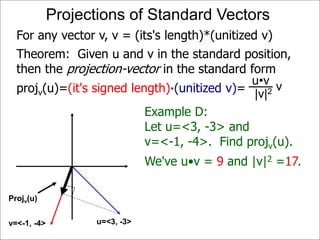
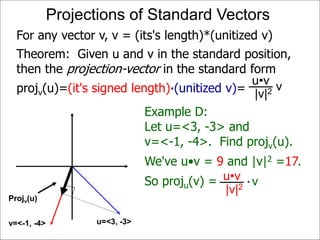
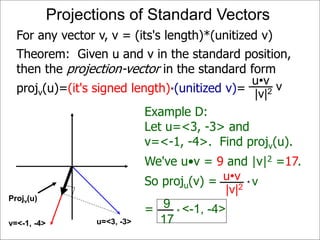
The document discusses unitizing vectors. In an example, a vector v = <3, 4> is unitized by rescaling it to obtain the unit vector <3/5, 4/5>. In general, to unitize a vector v, we divide it by its length |v| to obtain the unitized vector 1/|v| * v, which geometrically corresponds to shrinking or stretching v to have a length of 1.

1. Dot Product of Vectors

2. Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
Dot Product of Vectors

3. Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors

4. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors

5. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors

6. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors

7. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors

8. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>

9. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>

10. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>
= 15*4 + (-18)*(-5)
= 60 + 90 = 150

11. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>
= 15*4 + (-18)*(-5)
= 60 + 90 = 150 = 3(u  v)

12. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>
= 15*4 + (-18)*(-5)
= 60 + 90 = 150 = 3(u  v)
Facts: 1. u•v = v•u

13. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>
= 15*4 + (-18)*(-5)
= 60 + 90 = 150 = 3(u  v)
Facts: 1. u•v = v•u
2. For any scalar λ, λu • v = λ(u • v)

14. Example A: Let u = <5, -6>, v = <4, -5>
a. u  v = <5, -6>  <4, -5>
= 5*4 + (-6)*(-5)
= 20 + 30 = 50
Given u=<a, b>, v=<c, d>, the dot product of u
and v is u  v = <a, b>  <c, d> = ac + bd
The dot product of two vector is a number.
Dot Product of Vectors
b. 3u  v = 3<5, -6>  <4, -5>
= <15, -18>  <4, -5>
= 15*4 + (-18)*(-5)
= 60 + 90 = 150 = 3(u  v)
Facts: 1. u•v = v•u
2. For any scalar λ, λu • v = λ(u • v)
3. u•(v + w) = u•v + u•w

15. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Unitized Vectors

16. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
Unitized Vectors

17. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
Unitized Vectors

18. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
Unitized Vectors

19. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is1
5
1
5
Unitized Vectors

20. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is
|< , >| = * |<3, 4>|
1
5
1
5
3
5
4
5
1
5
Unitized Vectors

21. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is
|< , >| = * |<3, 4>| = * 5 = 1
1
5
1
5
3
5
4
5
1
5
1
5
Unitized Vectors

22. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is
|< , >| = * |<3, 4>| = * 5 = 1
1
5
1
5
3
5
4
5
1
5
1
5
Vector of length 1
are called unit vectors.
Unitized Vectors

23. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is
|< , >| = * |<3, 4>| = * 5 = 1
1
5
1
5
3
5
4
5
1
5
1
5
Vector of length 1
are called unit vectors.
<3/5, 4/5>
r = 1
Unit vectors
Unitized Vectors

24. Fact: Given v a vector, λ a scalar, then |λv| = |λ|*|v|.
Example B: Let v = <3, 4> so that | <3, 4> | = 5,
a: Let λ = 10, then the length of 10<3, 4> is
|<30, 40>| = 10 * 5 = 50
b: Let λ = , then the length of <3, 4> is
|< , >| = * |<3, 4>| = * 5 = 1
1
5
1
5
3
5
4
5
1
5
1
5
Vector of length 1
are called unit vectors.
In the above example,
3
5
4
5
< , > is a unit vector.
<3/5, 4/5>
r = 1
Unit vectors
Unitized Vectors

25. Unitized Vectors

26. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.3
5
4
5,

27. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,

28. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
From this example, we see that in general
the unitized v is 1
|v|
v

29. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
From this example, we see that in general
the unitized v is since | v | = 1.1
|v|
1
|v| |v| =
1
|v|
v

30. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
Geometrically, unitizing v
corresponds to shrinking
or stretching v to be a
unit vector.
From this example, we see that in general
the unitized v is since | v | = 1.1
|v|
1
|v| |v| =
1
|v|
v

31. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
From this example, we see that in general
the unitized v is since | v | = 1.1
|v|
1
|v| |v| =
1
|v|
v
Geometrically, unitizing v
corresponds to shrinking
or stretching v to be a
unit vector.
v
r=1
unitized v

32. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
Geometrically, unitizing v
corresponds to shrinking
or stretching v to be a
unit vector.
v
1
|v|
v
r=1
unitized v
unitized v
,
From this example, we see that in general
the unitized v is since | v | = 1.1
|v|
1
|v| |v| =
1
|v|
v

33. Unitized Vectors
In the above exampe b. we rescale the vector
v =<3, 4> and obtain < > which is a unit vector.
We say that we unitized v.
3
5
4
5,
Geometrically, unitizing v
corresponds to shrinking
or stretching v to be a
unit vector.
v
1
|v|
v
r=1
unitized v
unitized v
,
Unitized v is the only unit
vector that has the same
direction as v.
From this example, we see that in general
the unitized v is since | v | = 1.1
|v|
1
|v| |v| =
1
|v|
v

34. Dot product and Angles

35. Dot product and Angles
The following theorem put all the above concepts
together.

36. Dot product and Angles
Dot Product Theorem:
The following theorem put all the above concepts
together.

37. Dot product and Angles
Dot Product Theorem:
a. Let u and v be two unit vectors and  be
the angle between them, then cos() = u•v.
The following theorem put all the above concepts
together.

38. Dot product and Angles
Dot Product Theorem:
a. Let u and v be two unit vectors and  be
the angle between them, then cos() = u•v.
b. Let u and v be any two vectors and  be
the angle between them
cos() = (unitized u)  (unitized v)
The following theorem put all the above concepts
together.

39. Dot product and Angles
Dot Product Theorem:
a. Let u and v be two unit vectors and  be
the angle between them, then cos() = u•v.
b. Let u and v be any two vectors and  be
the angle between them
cos() = (unitized u)  (unitized v)
=  v
|v|
u
|u|
Easy to memorize
The following theorem put all the above concepts
together.

40. Dot product and Angles
Dot Product Theorem:
a. Let u and v be two unit vectors and  be
the angle between them, then cos() = u•v.
b. Let u and v be any two vectors and  be
the angle between them
cos() = (unitized u)  (unitized v)
=  =v
|v|
u
|u|
u•v
|u|*|v|
Easy to memorize Easier way to compute
The following theorem put all the above concepts
together.

41. Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.

42. uv=10,
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.

43. uv=10, |u|=10,
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.

44. uv=10, |u|=10, |v|=20,
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.

45. uv=10, |u|=10, |v|=20, hence,
cos() = =
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20

46. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20

47. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2)
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20

48. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20

49. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.

50. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>,

51. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>

52. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10

53. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10
|u + v| = 50,

54. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10
|u + v| = 50, |u – v| = 10

55. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10
|u + v| = 50, |u – v| = 10
So cos(A) = -10/500

56. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10
|u + v| = 50, |u – v| = 10
So cos(A) = -10/500  -0.447

57. uv=10, |u|=10, |v|=20, hence,
cos() = = = 10/200 = 1/2
So  = cos-1(1/2) = 45o
Dot product and Angles
Example C:
a. Let u = <3, -1> and v = <2, -4>. Find the angle 
between them.
u•v
|u|*|v|
10
10*20
b. Find the angle A between u + v and u – v.
u + v = <5, -5>, u – v = <1, 3>
(u + v)•(u – v) = 5 – 15 = -10
|u + v| = 50, |u – v| = 10
So cos(A) = -10/500  -0.447
A = cos-1(-0.447)  117o.

58. Dot product and Angles
Theorem: Given u, v two nonzero vectors such that
u•v=0, then u and v are perpendicular (orthorgonal).

59. Dot product and Angles
Theorem: Given u, v two nonzero vectors such that
u•v=0, then u and v are perpendicular (orthorgonal).
If  is the angle between them and u•v = 0,
then cos() = = 0.
u•v
|u|*|v|

60. Dot product and Angles
Theorem: Given u, v two nonzero vectors such that
u•v=0, then u and v are perpendicular (orthorgonal).
If  is the angle between them and u•v = 0,
then cos() = = 0.
Hence  = cos-1(0) = 90o
u•v
|u|*|v|

61. Example D: <5, -3>•<3, 5> = 15 – 15 = 0,
hence they are orthogonal.
Dot product and Angles
Theorem: Given u, v two nonzero vectors such that
u•v=0, then u and v are perpendicular (orthorgonal).
If  is the angle between them and u•v = 0,
then cos() = = 0.
Hence  = cos-1(0) = 90o
u•v
|u|*|v|

62.  2006, Frank Ma
Projections

63. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).

64. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).

65. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).projv (u)

66. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).projv (u)
Let  < 1800 be the angle between u and v,
the signed length of the projv(u) is |u |*cos().

67. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).projv (u)
If  is less than 90o then
cos() > 0, so |u|cos() is
also positive.
Let  < 1800 be the angle between u and v,
the signed length of the projv(u) is |u |*cos().

68. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).projv (u)
If  is less than 90o then
cos() > 0, so |u|cos() is
also positive. This means
the shadow is cast in the
direction of v.
Let  < 1800 be the angle between u and v,
the signed length of the projv(u) is |u |*cos().

69. Projections
The projection of the
vector u onto the vector v
is the vertically cast
shadow-vector of u onto v.
It is denoted as projv (u).projv (u)
If  is less than 90o then
cos() > 0, so |u|cos() is
also positive. This means
the shadow is cast in the
direction of v.
u
v
|u|cos() is positive means the
projv(u) is in the direction of v

 < 90o
Let  < 1800 be the angle between u and v,
the signed length of the projv(u) is |u |*cos().

70. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative.

71. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.

72. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.
u
v
|u|cos() is negative so projv(u)
is in the opposite direction of v.

 >90o

73. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.
u
v
|u|cos() is negative so projv(u)
is in the opposite direction of v.

 >90o

74. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.
u
v
|u|cos() is negative so projv(u)
is in the opposite direction of v.

Example A: Given that
the angle between u and v
is 67o and |u|=23, |v|=28.
Find the length of the
shadow projv(u). Draw.
 >90o

75. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.
u
v
|u|cos() is negative so projv(u)
is in the opposite direction of v.

Example A: Given that
the angle between u and v
is 67o and |u|=23, |v|=28.
Find the length of the
shadow projv(u). Draw.
|u|=23
67o
|v|=28
 >90o

76. Projections
If  is more than 90o then
cos() < 0, so |u|cos() is
negative. We get the
negative length of projv(u)
and projv(u) is cast in the
opposite direction of v.
u
v
|u|cos() is negative so projv(u)
is in the opposite direction of v.

Example A: Given that
the angle between u and v
is 67o and |u|=23, |v|=28.
Find the length of the
shadow projv(u). Draw.
|u|=23
67o
|v|=28
The length of projv(u) = |u|cos() = 23cos(67)  8.99
 >90o

77. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.

78. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28

79. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28

80. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28
The length of proju(v) = |v|cos()

81. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28
The length of proju(v) = |v|cos()
= 28cos(117)  -12.7

82. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28
The length of proju(v) = |v|cos()
= 28cos(117)  -12.7
Note the negative answer indicates the shadow is
cast in the opposite direction of u.

83. Projections
Example B: Given that the
angle between u and v is
117o and |u|=23, |v|=28.
Find the length of the
shadow proju(v). Draw.
|u|=23
117o |v|=28
The length of proju(v) = |v|cos()
= 28cos(117)  -12.7
Note the negative answer indicates the shadow is
cast in the opposite direction of u.
Your Turn: Given the angle
between u and v is 135o and
|u|=36, |v|=18. Draw and find
the length of the projv(u).
135o
|u|=36
v
Ans: Signed length of projv(u) = –36/2  –25.4
projv(u)

84. Signed Length of Standard Projection

85. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v.
Projv(u)
u
v
Signed Length of Standard Projection

86. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u•
v
|v|
Projv(u)
u
v
Signed Length of Standard Projection

87. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
Projv(u)
v
|v|
u•v
|v|
u
v
Signed Length of Standard Projection

88. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
v
|v|
u•v
|v|
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
Projv(u)
u
v
Signed Length of Standard Projection

89. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
Projv(u)
v
|v|
u•v
|v|
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
u=<3, -3>
v=<-1, -4>
Signed Length of Standard Projection

90. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
v
|v|
u•v
|v|
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
uv = <3,-3><-1,-4> = 9
Projv(u)
u=<3, -3>
v=<-1, -4>
Signed Length of Standard Projection

91. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
v
|v|
u•v
|v|
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
uv = <3,-3><-1,-4> = 9
|v|= 17,Projv(u)
u=<3, -3>
v=<-1, -4>
Signed Length of Standard Projection

92. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
Projv(u)
v
|v|
u•v
|v|
u
v
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
uv = <3,-3><-1,-4> = 9
|v|= 17, hence the length of
projv(u) is =
Projv(u)
u=<3, -3>
v=<-1, -4>
u•v
|v|
9
17
Signed Length of Standard Projection

93. Theorem: Given two vectors u and v in the
standard position, the signed length of projv(u) is
u dotted with unitized v. That is, the signed length
of projv(u) is u• or .
Projv(u)
v
|v|
u•v
|v|
u
v
Example C:
Let u=<3, -3> and
v=<-1, -4>. Find the length
of projv(u). Draw.
uv = <3,-3><-1,-4> = 9
|v|= 17, hence the length of
projv(u) is =
Projv(u)
u=<3, -3>
v=<-1, -4>
u•v
|v|
9
17
 2.18.
Signed Length of Standard Projection

94. Projections of Standard Vectors

95. Projections of Standard Vectors
For any vector v, v = (its's length)*(unitized v)

96. Projections of Standard Vectors
For any vector v, v = (its's length)*(unitized v)
Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)

97. Projections of Standard Vectors
For any vector v, v = (its's length)*(unitized v)
Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)= vu•v
|v|2

98. Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)=
Projections of Standard Vectors
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
vu•v
|v|2

99. Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)=
Projections of Standard Vectors
u=<3, -3>v=<-1, -4>
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
vu•v
|v|2

100. Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)=
Projv(u)
Projections of Standard Vectors
Projv(u)
u=<3, -3>v=<-1, -4>
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
vu•v
|v|2

101. Projv(u)
Projections of Standard Vectors
Projv(u)
u=<3, -3>v=<-1, -4>
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
We've u•v = 9 and |v|2 =17.
Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)= vu•v
|v|2

102. Projv(u)
Projections of Standard Vectors
Projv(u)
u=<3, -3>v=<-1, -4>
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
We've u•v = 9 and |v|2 =17.
So proju(v) = vu•v
|v|2 *
Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)= vu•v
|v|2

103. Projv(u)
Projections of Standard Vectors
Projv(u)
u=<3, -3>v=<-1, -4>
For any vector v, v = (its's length)*(unitized v)
Example D:
Let u=<3, -3> and
v=<-1, -4>. Find projv(u).
We've u•v = 9 and |v|2 =17.
So proju(v) = vu•v
|v|2 *
9
17
* <-1, -4>=
Theorem: Given u and v in the standard position,
then the projection-vector in the standard form
projv(u)=(it's signed length)*(unitized v)= vu•v
|v|2

104. HW
Given u=<-1,2>, v=<3,-2>, and w=<4,2>
find the signed length and the vectors for
each of the following:
1. proju(v) 2. projv(u) 3. projv(w)
4. proju(u+v) 5. projw(v – u)
6. proju+v (u – w) 7. projv+w (v + u)