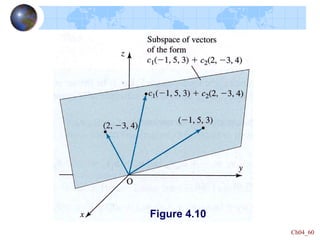
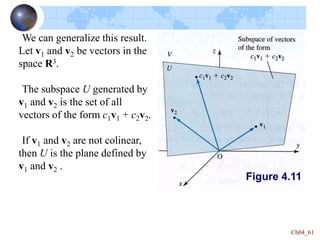
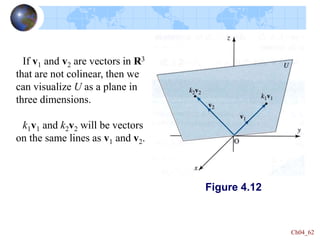
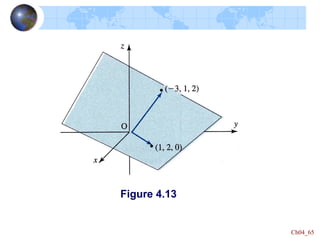
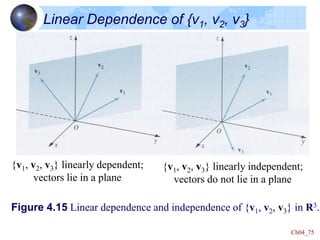
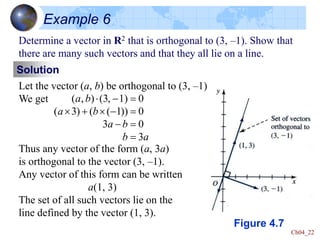
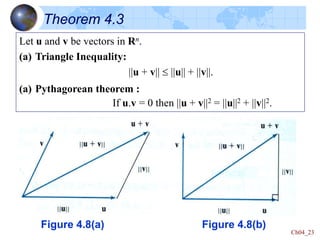
This document defines key concepts in linear algebra including vector spaces, vectors, and operations on vectors such as addition and scalar multiplication. It specifically focuses on the vector space Rn: - Rn is the set of all n-tuples of real numbers, which forms a vector space under component-wise addition and scalar multiplication. - The dot product and norm are defined for vectors in Rn and used to determine properties like orthogonality and the angle between vectors. - Examples show how to perform vector operations in Rn like addition, scalar multiplication, finding the dot product and norm, and determining if vectors are orthogonal.

1. Chapter 4
Ref Book:
Linear Algebra with Applications by Gareth Williams
8th Edition
Vector Spaces
Linear Algebra

2. Ch04_2
Definition 1.
Let be a sequence of n real numbers. The set of all
such sequences is called n-space (or n-dimensional. space) and
is denoted Rn.
u1 is the first component of .
u2 is the second component and so on.
)
...,
,
,
( 2
1 n
u
u
u
)
...,
,
,
( 2
1 n
u
u
u
Example 1
• R2 is the collection of all sets of two ordered real numbers.
For example, (0, 0) , (1, 2) and (-2, -3) are elements of R2.
• R3 is the collection of all sets of three ordered real numbers.
For example, (0,0, 0) and (-1,3, 4) are elements of R3.
4.1 The vector Space Rn

3. Ch04_3
Definition 2.
Let be two elements of Rn.
We say that u and v are equal if u1 = v1, …, un = vn.
Thus two elements of Rn are equal if their corresponding
components are equal.
)
...,
,
,
(
and
)
...,
,
,
( 2
1
2
1 n
n v
v
v
u
u
u 
 v
u
Definition 3.
Let be elements of Rn
and let c be a scalar. Addition and scalar multiplication are
performed as follows:
Addition:
Scalar multiplication :
)
...,
,
,
(
and
)
...,
,
,
( 2
1
2
1 n
n v
v
v
u
u
u 
 v
u
)
...,
,
(
)
...,
,
(
1
1
1
n
n
n
cu
cu
c
v
u
v
u





u
v
u

4. Ch04_4
► The set Rn with operations of componentwise addition and
scalar multiplication is an example of a vector space, and its
elements are called vectors.
We shall henceforth interpret Rn to be a vector space.
(We say that Rn is closed under addition and scalar multiplication).
► In general, if u and v are vectors in the same vector space, then u + v is
the diagonal of the parallelogram defined by u and v.
Figure 4.1

5. Ch04_5
Example 2
Let u = ( –1, 4, 3) and v = ( –2, –3, 1) be elements of R3.
Find u + v and 3u.
Solution: u + v = (–1, 4, 3) + (– 2, –3, 1) = (-3 ,1 ,4)
3u = 3 (–1, 4, 3) = (-3 ,12 ,9)
Example 3
Figure 4.2
In R2 , consider the two elements
(4, 1) and (2, 3).
Find their sum and give a geometrical
interpretation of this sum.
we get (4, 1) + (2, 3) = (6, 4).
The vector (6, 4), the sum, is the
diagonal of the parallelogram.

6. Ch04_6
Example 4
Figure 4.3
Consider the scalar multiple of the vector (3, 2) by 2, we get
2(3, 2) = (6, 4)
Observe in Figure 4.3 that (6, 4) is a vector in the same direction
as (3, 2), and 2 times it in length.

7. Ch04_7
Zero Vector
The vector (0, 0, …, 0), having n zero components, is called the
zero vector of Rn and is denoted 0.
Negative Vector
The vector (–1)u is writing –u and is called the negative of u.
It is a vector having the same length (or magnitude) as u, but
lies in the opposite direction to u.
Subtraction
Subtraction is performed on element of Rn by subtracting
corresponding components.
u
-u

8. Ch04_8
Theorem 4.1
Let u, v, and w be vectors in Rn and let c and d be scalars.
(a) u + v = v + u
(b) u + (v + w) = (u + v) + w
(c) u + 0 = 0 + u = u
(d) u + (–u) = 0
(e) c(u + v) = cu + cv
(f) (c + d)u = cu + du
(g) c(du) = (cd)u
(h) 1u = u
Figure 4.4
Commutativity of vector addition
u + v = v + u

9. Ch04_9
Example 5
Let u = (2, 5, –3), v = ( –4, 1, 9), w = (4, 0, 2) in the vector space R3.
Determine the vector 2u – 3v + w.
Solution
)
31
7,
20,
(
)
2
27
6
,
0
3
10
4,
12
(4
2)
0,
(4,
27)
3,
,
12
(
)
6
10,
,
4
(
2)
0,
(4,
9)
1,
,
4
(
3
)
3
5,
,
2
(
2
-


-
-

-




-
-
-


-
-
-


- w
3v
2u

10. Ch04_10
Column Vectors




























n
n
n
n v
u
v
u
v
v
u
u



1
1
1
1
We defined addition and scalar multiplication of column vectors
in Rn in a componentwise manner:
and

















n
n cu
cu
u
u
c 

1
1
Row vector:
Column vector:
)
...,
,
,
( 2
1 n
u
u
u

u










n
u
u

1

11. Ch04_11
Homework
Exercise set 1.3 page 33:
3, 5, 7, 9, 11

12. Ch04_12
4.2 Dot Product, Norm, Angle, and Distance
Definition
Let be two vectors in Rn.
The dot product of u and v is denoted u.v and is defined
by .
The dot product assigns a real number to each pair of vectors.
)
...,
,
,
(
and
)
...,
,
,
( 2
1
2
1 n
n v
v
v
u
u
u 
 v
u
n
nv
u
v
u 


 
1
1
v
u
Example 1
Find the dot product of
u = (1, –2, 4) and v = (3, 0, 2)
Solution
11
8
0
3
)
2
4
(
)
0
2
(
)
3
1
(







-



 v
u

13. Ch04_13
Properties of the Dot Product
Let u, v, and w be vectors in Rn and let c be a scalar. Then
1. u.v = v.u
2. (u + v).w = u.w + v.w
3. cu.v = c(u.v) = u.cv
4. u.u  0, and u.u = 0 if and only if u = 0
Proof
1.
u
v
v
u
v
u











numbers
real
of
property
e
commutativ
by the
get
We
).
...,
,
,
(
and
)
...,
,
,
(
Let
1
1
1
1
2
1
2
1
n
n
n
n
n
n
u
v
u
v
v
u
v
u
v
v
v
u
u
u


4.    
   
   
.
if
only
and
if
0
Thus
.
0
,
,
0
if
only
and
if
,
0
.
0
thus
,
0
1
2
2
1
2
2
1
2
2
1
1
1
0
u
u
u
u
u
u
u




















n
n
n
n
n
n
u
u
u
u
u
u
u
u
u
u
u
u






14. Ch04_14
Norm of a Vector in Rn
Definition
The norm (length or magnitude)
of a vector u = (u1, …, un) in Rn
is denoted ||u|| and defined by
Note:
The norm of a vector can also
be written in terms of
the dot product
   2
2
1 n
u
u 

 
u
u
u
u 

Figure 4.5 length of u

15. Ch04_15
Definition
A unit vector is a vector whose norm is 1.
If v is a nonzero vector, then the vector
is a unit vector in the direction of v.
This procedure of constructing a unit vector in the same direction
as a given vector is called normalizing the vector.
v
v
u
1

Find the norm of each of the vectors u = (1, 3, 5) of R3
and v = (3, 0, 1, 4) of R4.
Solution 35
25
9
1
)
5
(
)
3
(
)
1
( 2
2
2







u
26
16
1
0
9
)
4
(
)
1
(
)
0
(
)
3
( 2
2
2
2









v
Example 2

16. Ch04_16
Example 3
Solution
(a) Show that the vector (1, 0) is a unit vector.
(b) Find the norm of the vector (2, –1, 3). Normalize this vector.
(a) Thus (1, 0) is a unit vector. It can be
similarly shown that (0, 1) is a unit vector in R2.
.
1
0
1
0)
,
1
( 2
2



(b) The norm of (2, –1, 3) is
The normalized vector is
The vector may also be written
This vector is a unit vector in the direction of (2, –1, 3).
.
14
3
)
1
(
2
3)
,
1
,
2
( 2
2
2


-


- .
14
)
3
,
1
,
2
(
14
1
-
.
14
3
,
14
1
,
14
2





 -

17. Ch04_17
Angle between Vectors ( in R2)
← Figure 4.6
The law of cosines gives:

18. Ch04_18
Definition
Let u and v be two nonzero vectors in Rn.
The cosine of the angle  between these vectors is


 


 0
cos
v
u
v
u
Example 4
Determine the angle between the vectors u = (1, 0, 0) and
v = (1, 0, 1) in R3.
Solution 1
1)
0,
(1,
0)
0,
1,
( 


 v
u
2
1
0
1
1
0
0
1 2
2
2
2
2
2







 v
u
Thus the angle between u and v is 45.
,
2
1
cos 


v
u
v
u

Angle between Vectors (in R n)

19. Ch04_19
Definition
Two nonzero vectors are orthogonal if the angle between them is a
right angle .
Two nonzero vectors u and v are orthogonal if and only if u.v = 0.
Theorem 4.2
Proof
0
0
cos
orthogonal
are
, 



 v
u
v
u 
Orthogonal Vectors

20. Ch04_20
Solution
Example 5
Show that the following pairs of vectors are orthogonal.
(a) (1, 0) and (0, 1).
(b) (2, –3, 1) and (1, 2, 4).
(a) (1, 0).(0, 1) = (1  0) + (0  1) = 0.
The vectors are orthogonal.
(b) (2, –3, 1).(1, 2, 4) = (2  1) + (–3  2) + (1  4) = 2 – 6 + 4 = 0.
The vectors are orthogonal.

21. Ch04_21
Note
(1, 0), (0,1) are orthogonal unit vectors in R2.
(1, 0, 0), (0, 1, 0), (0, 0, 1) are orthogonal unit
vectors in R3.
(1, 0, …, 0), (0, 1, 0, …, 0), …, (0, …, 0, 1) are
orthogonal unit vectors in Rn.

22. Ch04_22
Example 6
Determine a vector in R2 that is orthogonal to (3, –1). Show that
there are many such vectors and that they all lie on a line.
Solution
Let the vector (a, b) be orthogonal to (3, –1).
We get
a
b
b
a
b
a
b
a
3
0
3
0
))
1
(
(
)
3
(
0
1)
,
3
(
)
,
(


-

-




-

Thus any vector of the form (a, 3a)
is orthogonal to the vector (3, –1).
Any vector of this form can be written
a(1, 3)
The set of all such vectors lie on the
line defined by the vector (1, 3).
Figure 4.7

23. Ch04_23
Theorem 4.3
Let u and v be vectors in Rn.
(a) Triangle Inequality:
||u + v||  ||u|| + ||v||.
(a) Pythagorean theorem :
If u.v = 0 then ||u + v||2 = ||u||2 + ||v||2.
Figure 4.8(a) Figure 4.8(b)

24. Ch04_24
Distance between Points
Let be two points in Rn.
The distance between x and y is denoted d(x, y) and is defined by
Note: We can also write this distance as follows.
)
...,
,
,
(
and
)
...,
,
,
( 2
1
2
1 n
n y
y
y
x
x
x 
 y
x
2
2
1
1 )
(
)
(
)
,
( n
n y
x
y
x
d -


-
 
y
x
y
x
y
x -

)
,
(
d
Example 7. Determine the distance between the points
x = (1,–2 , 3, 0) and y = (4, 0, –3, 5) in R4.
Solution
74
25
36
4
9
)
5
0
(
)
3
3
(
)
0
2
(
)
4
1
(
)
,
( 2
2
2
2





-



-
-

-

y
x
d
x
y
x-y
Note: ( , ) ( , ) ( )
It is clear that d d the symmetric property

x y y x

25. Ch04_25
Homework
Exercise set 1.6 page 55:
3, 5, 8, 10, 14, 15, 17, 26.

26. Ch04_26
4.3 General Vector Spaces
Definition
A vector space is a set V of elements called vectors, having
operations of addition and scalar multiplication defined on it
that satisfy the following conditions.
Let u, v, and w be arbitrary elements of V, and c and d are scalars.
• Closure Axioms
1. The sum u + v exists and is an element of V. (V is closed
under addition.)
2. cu is an element of V. (V is closed under scalar multiplication.)
Our aim in this section will be to focus on the algebraic
properties of Rn.

27. Ch04_27
Example 1
(1) V={ …, -3, -1, 1, 3, 5, 7, …}
V is not closed under addition because 1+3=4  V.
(2) Z={ …, -2, -1, 0, 1, 2, 3, 4, …}
Z is closed under addition because
for any a, b  Z, a + b Z.
Z is not closed under scalar multiplication because
½ is a scalar, for any odd a  Z, (½)a  Z.

28. Ch04_28
• Addition Axioms
3. u + v = v + u (commutative property)
4. u + (v + w) = (u + v) + w (associative property)
5. There exists an element of V, called the zero vector, denoted 0,
such that u + 0 = u.
6. For every element u of V there exists an element called the
negative of u, denoted -u, such that u + (-u) = 0.
• Scalar Multiplication Axioms
7. c(u + v) = cu + cv
8. (c + d)u = cu + du
9. c(du) = (cd)u
10. 1u = u
Definition of Vector Space (continued)

29. Ch04_29
W.
Thus W is closed under scalar multiplication.
A Vector Space in R3
Let , for some a, bR.
W
b
a )
1
,
0
,
1
(
and
)
1
,
0
,
1
( 

 v
u
Axiom 1:
u + v W. Thus W is closed under addition.
)
1
,
0
,
1
)(
(
)
1
,
0
,
1
(
)
1
,
0
,
1
( b
a
b
a 



 v
u
Axiom 3,4 and 7~10: trivial
}.
|
1)
0,
(1,
{
Let R

 a
a
W Prove that W is a vector space.
Proof
)
1
,
0
,
1
(
ca
c 
u
Axiom 2:
Axiom 5: Let 0 = (0, 0, 0) = 0(1,0,1),
then 0 W and 0+u = u+0 = u for any u  W.
Axiom 6: For any u = a(1,0,1)  W. Let -u = -a(1,0,1),
then -u W and (-u)+u = 0.

30. Ch04_30
Vector Spaces of Matrices (Mmn)
Let .
and 22
M
h
g
f
e
d
c
b
a














 v
u
Axiom 1:
u + v is a 2  2 matrix. Thus M22 is closed under addition.
► Question: Prove Axiom 2 and Axiom 7 .


























h
d
g
c
f
b
e
a
h
g
f
e
d
c
b
a
v
u
Axiom 3 and 4:
From our previous discussions we know that 2  2 matrices are
commutative and associative under addition (Theorem 2.2).
}.
,
,
,
|
{
Let 22 R







 s
r
q
p
s
r
q
p
M Prove that M22 is a vector space.
Proof

31. Ch04_31
{ | , , , 0} a vector space?
p q
Is the set W p q r s
r s
 
 
 
 
Axiom 5:
The 2  2 zero matrix is , since







0
0
0
0
0
u
0
u 






















d
c
b
a
d
c
b
a
0
0
0
0
Axiom 6:
0
u
u
u
u














-
-
-
-







-
-
-
-








-







-
-
-
-

-







0
0
0
0
d
d
c
c
b
b
a
a
d
c
b
a
d
c
b
a
d
c
b
a
d
c
b
a
)
(
since
,
then
,
If
In general: The set of m  n matrices, Mmn, is a vector space.

32. Ch04_32
Vector Spaces of Functions
Axiom 1:
f + g is defined by (f + g)(x) = f(x) + g(x).
 f + g : R R
 f + g  F. Thus F is closed under addition.
Axiom 2:
cf is defined by (cf)(x) = c f(x).
 cf : R R
 cf  F. Thus F is closed under scalar multiplication.
Prove that F = { f | f: R R } is a vector space.
Let f, g  F, c  R. For example: f: R R, f(x)=2x,
g: R R, g(x)=x2+1.

33. Ch04_33
Vector Spaces of Functions (continued)
Axiom 5:
Let 0 be the function such that 0(x) = 0 for every xR.
0 is called the zero function.
We get (f + 0)(x) = f(x) + 0(x) = f(x) + 0 = f(x) for every xR.
Thus f + 0 = f. (0 is the zero vector.)
Axiom 6:
Let the function –f defined by (-f )(x) = -f (x).
Thus [f + (-f )] = 0, -f is the negative of f.
)
(
0
)]
(
[
)
(
)
)(
(
)
(
)
)](
(
[
x
x
f
x
f
x
f
x
f
x
f
f
0


-

-


-

Is the set F ={ f | f(x)=ax2+bx+c for some a,b,c R} a vector space?

34. Ch04_34
Theorem 4.4 (useful properties)
Let V be a vector space, v a vector in V, 0 the zero vector of V,
c a scalar, and 0 the zero scalar. Then
(a) 0v = 0
(b) c0 = 0
(c) (-1)v = -v
(d) If cv = 0, then either c = 0 or v = 0.

35. Ch04_35
Homework
Exercise set 4.1, pages 206-207:
5, 7, 11, 13, 15.

36. Ch04_36
4.4 Subspaces
Figure 4.9

37. Ch04_37
Definition
Let V be a vector space and U be a nonempty subset of V.
U is said to be a subspace of V if it is closed under addition
and under scalar multiplication.
Note:
► In general, a subset of a vector space may or may not satisfy
the closure axioms.
► However, any subset that is closed under both of these
operations satisfies all the other vector space properties.

38. Ch04_38
Example 1
Let U be the subset of R3 consisting of all vectors of the form
(a, 0, 0) (with zeros as second and third components and aR ),
i.e., U = {(a, 0, 0)  R3 }.
Show that U is a subspace of R3.
Solution
Let (a, 0, 0), (b, 0, 0)  U, and let k R.
We get
(a, 0, 0) + (b, 0, 0) = (a + b, 0, 0)  U
k(a, 0, 0) = (k a, 0, 0)  U
The sum and scalar product are in U.
Thus U is a subspace of R3. #
Geometrically, U is the set of vectors that lie on the x-axis.

39. Ch04_39
Example 2
Let V be the set of vectors of of R3 of the form (a, a2, b), namely
V = {(a, a2, b)  R3 }.
Show that V is not a subspace of R3.
Solution
Let (a, a2, b), (c, c2, d)  V.
(a, a2, b) + (c, c2, d) = (a+ c, a2 + c2, b + d)
 (a + c, (a + c)2, b + d) ,
since a2 + c2  (a + c)2 .
Thus (a, a2, b) + (c, c2, d)  V.
V is not closed under addition.
V is not a subspace.

40. Ch04_40
Example 3
Prove that the set W of 2  2 diagonal matrices is a subspace of
the vector space M22 of 2  2 matrices.
Solution
(+) Let W.














q
p
b
a
0
0
and
0
0
v
u
We get
 u + v  W.
 W is closed under addition.
























q
b
p
a
q
p
b
a
0
0
0
0
0
0
v
u
() Let c R. We get
 cu  W.
 W is closed under scalar multiplication.
 W is a subspace of M22.














cb
ca
b
a
c
c
0
0
0
0
u

41. Ch04_41
The vector space of polynomials (Pn)
Example 5. Let Pn denoted the set of real polynomial functions of
degree  n. Prove that Pn is a vector space if addition and scalar
multiplication are defined on polynomials in a pointwise manner.
Solution
Let f and g  Pn, where
1
1 1 0
1
1 1 0
( ) ... and
( ) ...
n n
n n
n n
n n
f x a x a x a x a
g x b x b x b x b
-
-
-
-
    
    
►(+)
(f + g)(x) is a polynomial of degree  n.
Thus f + g  Pn.
Then Pn is closed under addition.
)
(
)
(
...
)
(
)
(
]
...
[
]
...
[
)
(
)
(
)
)(
(
0
0
1
1
1
1
1
0
1
1
1
0
1
1
1
b
a
x
b
a
x
b
a
x
b
a
b
x
b
x
b
x
b
a
x
a
x
a
x
a
x
g
x
f
x
g
f
n
n
n
n
n
n
n
n
n
n
n
n
n
n






















-
-
-
-
-
-
-
Example 4.

42. Ch04_42
►() Let c R,
(cf )(x) is a polynomial of degree  n.
So cf  Pn.
Then Pn is closed under scalar multiplication.
In conclusion : By (+) and (), Pn is a subspace of the vector
space F of functions.
Therefore Pn is itself a vector space.
0
1
1
1
0
1
1
1
...
]
...
[
)]
(
[
)
)(
(
ca
x
ca
x
ca
x
ca
a
x
a
x
a
x
a
c
x
f
c
x
cf
n
n
n
n
n
n
n
n











-
-
-
-

43. Ch04_43
Theorem 4.5 (Very important condition)
Let U be a subspace of a vector space V.
U contains the zero vector of V.
Note. Let 0 be the zero vector of V.
If 0 U  U is not a subspace of V.
If 0 U  (+)() hold  U is a subspace of V.
(+)() failed U is not a subspace of V.
Caution. This condition is necessary but not sufficient.
(See, for instance, Example 2 above and Example 5 below)

44. Ch04_44
Example 5
Let W be the set of vectors of the form (a, a, a+2).
Show that W is not a subspace of R3.
Solution
If (a, a, a+2) = (0, 0, 0), then a = 0 and a + 2 = 0 .
This system is inconsistent it has no solution.
Thus (0, 0, 0)  W. (The necessary condition does not hold)
 W is not a subspace of R3.

45. Ch04_45
Homework
Exercise set 4.1, pages 207-208:
19, 21, 23, 25, 27, 29, 31, 33.
Exercise set 1.3, page 32: 11, 12, 13, 15.
Let F ={ f | f: R R } the vector space of functions on R.
Which of the following are subspaces of F ?
(a) W1={ f | f: R R, f(0)=0 }.
(b) W2={ f | f: R R, f(0)=3 }.
(c) W3={ f | f: R R, for some cR, f(x)=c for every x}.
Exercise

46. Ch04_46
4.5 Linear Combinations of Vectors
W={(a, a, b) | a,b R}  R3
(a, a, b) = a (1,1,0) + b (0,0,1)
W is generated by (1,1,0) and (0,0,1).
e.g., (2, 2, 3) = 2 (1,1,0) + 3 (0,0,1)
(-1, -1, 7) = -1 (1,1,0) + 7 (0,0,1).
Definition
Let v1, v2, …, vm be vectors in a vector space V.
We say that v, a vector of V, is a linear combination of
v1, v2, …, vm , if there exist scalars c1, c2, …, cm such that
v can be written v = c1v1 + c2v2 + … + cmvm .

47. Ch04_47
The vector (5, 4, 2) is a linear combination of the vectors
(1, 2, 0), (3, 1, 4), and (1, 0, 3), since it can be written
(5, 4, 2) = (1, 2, 0) + 2(3, 1, 4) – 2(1, 0, 3)
Example 1

48. Ch04_48
Example 2
Determine whether or not the vector (-1, 1, 5) is a linear
combination of the vectors (1, 2, 3), (0, 1, 4), and (2, 3, 6).
Solution
Suppose 5)
1,
1,
(
6)
3,
(2,
4)
1,
(0,
3)
2,
(1, 3
2
1 -


 c
c
c
)
5
,
1
,
1
(
)
6
4
3
,
3
2
,
2
(
)
5
,
1
,
1
(
)
6
,
3
,
2
(
)
4
,
,
0
(
)
3
,
2
,
(
3
2
1
3
2
1
3
1
3
3
3
2
2
1
1
1
-






-



c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
1
,
2
,
1
5
6
4
3
1
3
2
1
2
3
2
1
3
2
1
3
2
1
3
1
-















-


 c
c
c
c
c
c
c
c
c
c
c
Thus (-1, 1, 5) is a linear combination of (1, 2, 3), (0, 1, 4), and
(2, 3, 6), where 6).
3,
(2,
1
4)
1,
(0,
2
3)
2,
(1,
5)
1,
1,
( -


-

49. Ch04_49
Example 3
Express the vector (4, 5, 5) as a linear combination of the vectors
(1, 2, 3), (-1, 1, 4), and (3, 3, 2).
Solution
Suppose 5)
5,
(4,
2)
3,
(3,
4)
1,
1
(
3)
2,
(1, 3
2
1 

-
 c
,
c
c
)
5
,
5
,
4
(
)
2
4
3
,
3
2
,
3
(
)
5
,
5
,
4
(
)
2
,
3
,
3
(
)
4
,
,
(
)
3
,
2
,
(
3
2
1
3
2
1
3
2
1
3
3
3
2
2
2
1
1
1






-


-

c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
r
c
r
c
r
c
c
c
c
c
c
c
c
c
c

-


-















-
 3
2
1
3
2
1
3
2
1
3
2
1
,
1
,
3
2
5
2
4
3
5
3
2
4
3
Thus (4, 5, 5) can be expressed in many ways as a linear
combination of (1, 2, 3), (-1, 1, 4), and (3, 3, 2):
6)
3,
,
2
(
4)
1,
,
1
(
)
1
(
3)
2,
(1,
)
3
2
(
5)
5,
,
4
( r
r
r 
-
-


-


50. Ch04_50
Example 4
Show that the vector (3, -4, -6) cannot be expressed as a linear
combination of the vectors (1, 2, 3), (-1, -1, -2), and (1, 4, 5).
Solution
Suppose

)
6
,
4
,
3
(
5)
4,
(1,
2)
,
1
1
(
3)
2,
(1, 3
2
1 -
-


-
-
-
 c
,
c
c
6
5
2
3
4
4
2
3
3
2
1
3
2
1
3
2
1





-


-
-


-


-
c
c
c
c
c
c
c
c
c
This system has no solution.
Thus (3, -4, -6) is not a linear combination of the vectors
(1, 2, 3), (-1, -1, -2), and (1, 4, 5).

51. Ch04_51
Example 5
Determine whether the matrix is a linear combination
of the matrices in the vector space
M22 of 2  2 matrices.






-
-
1
8
7
1











 -






0
2
1
0
and
,
2
0
3
2
,
1
2
0
1
Solution
Suppose






-
-













 -







1
8
7
1
0
2
1
0
2
0
3
2
1
2
0
1
3
2
1 c
c
c






-
-










-

1
8
7
1
2
2
2
3
2
2
1
3
1
3
2
2
1
c
c
c
c
c
c
c
c
Then

52. Ch04_52







-






-
-


1
2
8
2
2
7
3
1
2
2
1
3
1
3
2
2
1
c
c
c
c
c
c
c
c
This system has the unique solution c1 = 3, c2 = -2, c3 = 1.
Therefore












 -
-













-
-
0
2
1
0
2
0
3
2
2
1
2
0
1
3
1
8
7
1

53. Ch04_53
Example 6
Determine whether the function is a linear
combination of the functions and
7
10
)
( 2
-

 x
x
x
f
Solution
Suppose .
2
1 f
h
c
g
c 

7
10
)
4
2
(
)
1
3
( 2
2
2
2
1 -



-

-
 x
x
x
x
c
x
x
c
Then
1
3
)
( 2
-

 x
x
x
g
.
4
2
)
( 2

-
 x
x
x
h
7
10
4
)
3
(
)
2
( 2
2
1
2
1
2
2
1 -



-
-

 x
x
c
c
x
c
c
x
c
c





-


-

-



7
4
10
3
1
2
2
1
2
1
2
1
c
c
c
c
c
c
1
,
3 2
1 -


 c
c .
3 h
g
f -



54. Ch04_54
Definition
The vectors v1, v2, …, vm are said to span a vector space if every
vector in the space can be expressed as a linear combination of
these vectors.
In this case {v1, v2, …, vm} is called a spanning set.
Spanning Sets

55. Ch04_55
Show that the vectors (1, 2, 0), (0, 1, -1), and (1, 1, 2) span R3.
Solution
Let (x, y, z) be an arbitrary element of R3.
Suppose )
2
,
1
,
1
(
)
1
,
1
,
0
(
)
0
,
2
,
1
(
)
,
,
( 3
2
1 c
c
c
z
y
x 
-


)
2
,
2
,
(
)
,
,
( 3
2
3
2
1
3
1 c
c
c
c
c
c
c
z
y
x 
-





Example 7







-





z
c
c
y
c
c
c
x
c
c
3
2
3
2
1
3
1
2
2







-



-

-
-

z
y
x
c
z
y
x
c
z
y
x
c
2
2
4
3
3
2
1
 
The vectors (1, 2, 0), (0, 1, -1), and (1, 1, 2) span R3.
)
2
,
1
,
1
)(
2
(
)
1
,
1
,
0
)(
2
4
(
)
0
,
2
,
1
)(
3
(
)
,
,
( z
y
x
z
y
x
z
y
x
z
y
x 

-

-


-

-
-



56. Ch04_56
Example 8
Show that the following matrices span the vector space M22 of
2  2 matrices.
























1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
Solution






d
c
b
a
Let  M22 (an arbitrary element).
We can express this matrix as follows:
proving the result.


































1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
d
c
b
a
d
c
b
a

57. Ch04_57
Theorem 4.6
Let v1, …, vm be vectors in a vector space V. Let U be the set
consisting of all linear combinations of v1, …, vm .
Then U is a subspace of V spanned by the vectors v1, …, vm .
U is said to be the vector space generated by v1, …, vm .
Proof
(+) Let u1 = a1v1 + … + amvm and u2 = b1v1 + … + bmvm  U.
Then u1 + u2 = (a1v1 + … + amvm) + (b1v1 + … + bmvm)
= (a1 + b1) v1 + … + (am + bm) vm
 u1 + u2 is a linear combination of v1, …, vm .
 u1 + u2  U.
 U is closed under vector addition.

58. Ch04_58
()Let c R. Then
cu1 = c(a1v1 + … + amvm)
= ca1v1 + … + camvm
 cu1 is a linear combination of v1, …, vm .
 cu1  U.
 U is closed under scalar multiplication.
Thus U is a subspace of V.
By the definition of U, every vector in U can be written as a
linear combination of v1, …, vm .
Thus v1, …, vm span U.

59. Ch04_59
Example 9
Consider the vector space R3.
The vectors (-1, 5, 3) and (2, -3, 4) are in R3.
Let U be the subset of R3 consisting of all vectors of the form
c1(-1, 5, 3) + c2(2, -3, 4)
Then U is a subspace of R3 spanned by (-1, 5, 3) and (2, -3, 4).
The following are examples of some of the vectors in U, obtained
by given c1 and c2 various values.
)
8
1
,
1
,
4
(
vector
;
3
,
2
)
0
,
0
,
0
(
vector
;
0
,
0
)
4
,
3
,
2
(
vector
;
1
,
0
)
3
,
5
,
1
(
vector
;
0
,
1
2
1
2
1
2
1
2
1




-


-


c
c
c
c
c
c
c
c
We can visualize U. U is made up of all vectors in the plane
defined by the vectors (-1, 5, 3) and (2, -3, 4).

60. Ch04_60
Figure 4.10

61. Ch04_61
We can generalize this result.
Let v1 and v2 be vectors in the
space R3.
The subspace U generated by
v1 and v2 is the set of all
vectors of the form c1v1 + c2v2.
If v1 and v2 are not colinear,
then U is the plane defined by
v1 and v2 .
Figure 4.11

62. Ch04_62
Figure 4.12
If v1 and v2 are vectors in R3
that are not colinear, then we
can visualize U as a plane in
three dimensions.
k1v1 and k2v2 will be vectors
on the same lines as v1 and v2.

63. Ch04_63
Example 10
Let U be the subspace of R3 generated by the vectors (1, 2, 0) and
(-3, 1, 2). Let V be the subspace of R3 generated by the vectors
(-1, 5, 2) and (4, 1, -2). Show that U = V.
(U V) Let u be a vector in U. Let us show that u is in V.
Since u is in U, there exist scalars a and b such that
Let us see if we can write u as a linear combination of (-1, 5, 2)
and (4, 1, -2).
Such p and q would have to satisfy
Solution
)
2
,
2
,
3
(
)
2
,
1
,
3
(
)
0
,
2
,
1
( b
b
a
b
a
b
a 
-

-


u
)
2
2
,
5
,
4
(
)
2
-
,
1
,
4
(
)
2
,
5
,
1
( q
p
q
p
q
p
q
p -


-


-

u
b
q
p
b
a
q
p
b
a
q
p
2
2
2
2
5
3
4

-



-


-

64. Ch04_64
This system of equations has unique solution
Thus u can be written
Therefore, u is a vector in V.
.
3
2
,
3
b
a
q
b
a
p
-



)
2
,
1
,
4
(
3
2
)
2
,
5
,
1
(
3
-
-

-


b
a
b
a
u
(V U) Let v be a vector in V. Let us show that v is in U.
Since v is in V, there exist scalars c and d such that
It can be shown that
)
2
1
4
(
)
2
,
5
,
1
( -

-
 ,
,
d
c
v
)
2
,
1
,
3
)(
(
)
0
,
2
,
1
)(
2
( -
-


 d
c
d
c
v
Therefore, v is a vector in U and hence U=V.

65. Ch04_65
Figure 4.13

66. Ch04_66
Example 11
Let U be the vector space generated by the functions f(x) = x + 1
and g(x) = 2x2 – 2x + 3. Show that the function h(x) = 6x2–10x+5
lies in U.
Solution
h will be in the space generated by f and g if there exist scalars a
and b such that
a(x + 1) + b(2x2 – 2x + 3) = 6x2 – 10x + 5
This given
2bx2 + (a – 2b)x + a + 3b = 6x2 – 10x + 5
2b = 6
 a – 2b = – 10
a + 3b = 5
This system has the unique solution a = – 4, b = 3.
Thus – 4(x + 1) + 3(2x2 – 2x + 3) = 6x2 – 10x + 5

67. Ch04_67
Homework
Exercise set 4.2 pages 214-215:
1, 2, 3, 5, 7, 9, 11, 15, 17.

68. Ch04_68
4.6 Linear Dependence and Independence
Definition
(a) The set of vectors { v1, …, vm } in a vector space V is said to
be linearly dependent if there exist scalars c1, …, cm, not all
zero, such that c1v1 + … + cmvm = 0
(b) The set of vectors { v1, …, vm } is linearly independent if
c1v1 + … + cmvm = 0 can only be satisfied when
c1 = 0, …, cm = 0.
The concepts of dependence and independence of vectors are
useful tools in constructing “efficient” spanning sets for vector
spaces – sets in which there are no redundant vectors.

69. Ch04_69
Example 1
Show that the set {(1, 2, 3), (-2, 1, 1), (8, 6, 10)} is linearly
dependent in R3.
Solution
Suppose

0


-
 )
10
,
6
,
8
(
)
1
,
1
,
2
(
)
3
,
2
,
1
( 3
2
1 c
c
c
0
0






-


-

)
10
3
,
6
2
,
8
2
(
)
10
,
6
,
8
(
)
,
,
2
(
)
3
,
2
,
(
3
2
1
3
2
1
3
2
1
3
3
3
2
2
2
1
1
1
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
Thus
The set of vectors is linearly dependent.
0

-
-
- )
10
,
6
,
8
(
)
1
,
1
,
2
(
2
)
3
,
2
,
1
(
4
c1 = 4
c2 = -2
c3 = -1














-

0
10
3
0
6
2
0
8
2
3
2
1
3
2
1
3
2
1
c
c
c
c
c
c
c
c
c

70. Ch04_70
Example 2
Show that the set {(3, -2, 2), (3, -1, 4), (1, 0, 5)} is linearly
independent in R3.
Suppose

0


-

- )
5
,
0
,
1
(
)
4
,
1
,
3
(
)
2
,
2
,
3
( 3
2
1 c
c
c
0
0



-
-




-

-
)
5
4
2
,
2
,
3
3
(
)
5
,
0
,
(
)
4
,
,
3
(
)
2
,
2
,
3
(
3
2
1
2
1
3
2
1
3
3
2
2
2
1
1
1
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
Solution

This system has the unique solution c1 = 0, c2 = 0, and c3 = 0.
Thus the set is linearly independent.









-
-



0
5
4
2
0
2
0
3
3
3
2
1
2
1
3
2
1
c
c
c
c
c
c
c
c

71. Ch04_71
Example 3
Consider the functions f(x) = x2 + 1, g(x) = 3x – 1, h(x) = – 4x + 1
of the vector space P2 of polynomials of degree  2.
Show that the set of functions { f, g, h } is linearly independent.
Solution
Suppose
c1f + c2g + c3h = 0
Since for any real number x,
Consider three convenient values of x. We get
0


-

-

 )
1
4
(
)
1
3
(
)
1
( 3
2
2
1 x
c
x
c
x
c
0
5
4
2
:
1
0
3
2
2
:
1
0
:
0
3
2
1
3
2
1
3
2
1


-
-


-




-

c
c
c
x
c
c
c
x
c
c
c
x

72. Ch04_72
It can be shown that this system of three equations has the unique
solution
c1 = 0, c2 = 0, c3 = 0
Thus c1f + c2g + c3h = 0 implies that c1 = 0, c2 = 0, c3 = 0.
The set { f, g, h } is linearly independent.

73. Ch04_73
Theorem 4.7
A set consisting of two or more vectors in a vector space is
linearly dependent if and only if it is possible to express one
of the vectors as a linearly combination of the other vectors.
Example 4
The set of vectors {v1=(1, 2, 1) , v2 =(-1, -1, 0) , v3 = (0, 1,1)}
is linearly dependent, since v3 = v1 + v2 .
Thus, v3 is a linear combination of v1 and v2.
m

74. Ch04_74
Linear Dependence of {v1, v2}
{v1, v2} linearly dependent;
vectors lie on a line
{v1, v2} linearly independent;
vectors do not lie on a line
Figure 4.14 Linear dependence and independence of {v1, v2} in R3.

75. Ch04_75
Linear Dependence of {v1, v2, v3}
{v1, v2, v3} linearly dependent;
vectors lie in a plane
{v1, v2, v3} linearly independent;
vectors do not lie in a plane
Figure 4.15 Linear dependence and independence of {v1, v2, v3} in R3.

76. Ch04_76
Theorem 4.8
Let V be a vector space. Any set of vectors in V that contains the
zero is linearly dependent.
Proof
Consider the set { 0, v2, …, vm }, which contains the zero vectors.
Let us examine the identity
0
v
v
0 


 m
m
c
c
c 
2
2
1
We see that the identity is true for c1 = 1, c2 = 0, …, cm = 0 (not
all zero).
Thus the set of vectors is linearly dependent, proving the theorem.

77. Ch04_77
Theorem 4.9
Let the set {v1, …, vm} be linearly dependent in a vector space V.
Any set of vectors in V that contains these vectors will also be
linearly dependent.
Example 5
The set of vectors
{v1=(1, 2, 1) , v2 =(-1, -1, 0) , v3 = (0, 1,1) , v4 =( 1, 1, 1) }
is linearly dependent, since it contains the vectors v1 , v2 , v3
which are linearly dependent.

78. Ch04_78
Homework
Exercise set 4.3 pages 219-220:
1, 3, 7, 8, 9, 13, 15, 17.

79. Ch04_79
4.7 Bases and Dimension
Definition
A finite set of vectors {v1, …, vm} is called a basis for a vector
space V if the set spans V and is linearly independent.
Standard Basis
The set of n vectors
{(1, 0, …, 0), (0, 1, …, 0), …, (0, …, 1)}
is a basis for Rn. This basis is called the standard basis for Rn.
How to prove it?

80. Ch04_80
Example 1
Show that the set {(1, 0, -1), (1, 1, 1), (1, 2, 4)} is a basis for R3.
Solution
(span)
Let (x1, x2, x3) be an arbitrary element of R3.
Suppose
)
4
,
2
,
1
(
)
1
,
1
,
1
(
)
1
,
0
,
1
(
)
,
,
( 3
2
1
3
2
1 a
a
a
x
x
x 

-

Thus the set spans the space.
3
3
2
1
2
3
2
1
3
2
1
4
2
x
a
a
a
x
a
a
x
a
a
a



-






3
2
1
3
3
2
1
2
3
2
1
1
2
2
5
2
3
2
x
x
x
a
x
x
x
a
x
x
x
a

-

-

-


-



81. Ch04_81
0
4
0
2
0
3
2
1
3
2
3
2
1



-





b
b
b
b
b
b
b
b
(linearly independent)
Consider the identity
The identity leads to the system of equations
)
0
,
0
,
0
(
)
4
,
2
,
1
(
)
1
,
1
,
1
(
)
1
,
0
,
1
( 3
2
1 


- b
b
b
 b1 = 0, b2 = 0, and b3 = 0 is the unique solution.
Thus the set is linearly independent.
 {(1, 0, -1), (1, 1, 1), (1, 2, 4)} spans R3 and is linearly
independent.
 It forms a basis for R3.

82. Ch04_82
Example 2
Show that { f, g, h }, where f(x) = x2 + 1, g(x) = 3x – 1, and h(x)
= –4x + 1 is a basis for P2.
Solution
(linearly independent) see Example 3 of the previous section.
(span). Let p be an arbitrary function in P2.
p is thus a polynomial of the form
d
cx
bx
x
p 

 2
)
(
Suppose )
(
)
(
)
(
)
( 3
2
1 x
h
a
x
g
a
x
f
a
x
p 


for some scalars a1, a2, a3.
This gives
)
(
)
4
3
(
)
1
4
(
)
1
3
(
)
1
(
3
2
1
3
2
2
1
3
2
2
1
2
a
a
a
x
a
a
x
a
x
a
x
a
x
a
d
cx
bx

-

-



-

-






83. Ch04_83
Thus the polynomial p can be expressed
The functions f, g, and h span P2.
They form a basis for P2.
)
(
)
(
)
(
)
( 3
2
1 x
h
a
x
g
a
x
f
a
x
p 


d
a
a
a
c
a
a
b
a


-

-

3
2
1
3
2
1
4
3

c
d
b
a
c
d
b
a
b
a
-
-

-
-


3
3
4
4
3
2
1


84. Ch04_84
Theorem 4.10
Let {v1, …, vn } be a basis for a vector space V.
If {w1, …, wm} is a set of more than n vectors in V, then this set
is linearly dependent.
Proof
Suppose
(1)
We will show that values of c1, …, cm are not all zero.
0
1
1 

 m
m
c
c w
w 
The set {v1, …, vn} is a basis for V. Thus each of the vectors
w1, …, wm can be expressed as a linear combination of v1, …, vn.
Let
n
mn
m
m
m
n
n
a
a
a
a
a
a
v
v
v
w
v
v
v
w











2
2
1
1
1
2
12
1
11
1

85. Ch04_85
Substituting for w1, …, wm into Equation (1) we get
0
v
v
v
v
v
v 







 )
(
)
( 2
2
1
1
1
2
12
1
11
1 n
mn
m
m
m
n
n a
a
a
c
a
a
a
c 


0
v
v 







 n
mn
m
n
n
m
m a
c
a
c
a
c
a
c
a
c
a
c )
(
)
( 2
2
1
1
1
1
21
2
11
1 


Since v1, …, vn are linear independent,
0
0
2
2
1
1
1
2
21
1
11








m
mn
n
n
m
m
c
a
c
a
c
a
c
a
c
a
c
a



Since m > n, there are many solutions in this system.
Rearranging, we get
Thus the set {w1, …, wm} is linearly dependent.

86. Ch04_86
Theorem 4.11
Any two bases for a vector space V consist of the same number
of vectors.
Proof
Let {v1, …, vn} and {w1, …, wm} be two bases for V.
Thus n = m.
By Theorem 4.10,
m  n and n  m

87. Ch04_87
Definition
If a vector space V has a basis consisting of n vectors, then the
dimension of V is said to be n. We write dim(V) for the
dimension of V.
• V is finite dimensional if such a finite basis exists.
• V is infinite dimensional otherwise.

88. Ch04_88
Example 3
Consider the set {{1, 2, 3), (-2, 4, 1)} of vectors in R3.
These vectors generate a subspace V of R3 consisting of all
vectors of the form
The vectors (1, 2, 3) and (-2, 4, 1) span this subspace.
)
1
,
4
,
2
(
)
3
,
2
,
1
( 2
1 -

 c
c
v
Furthermore, since the second vector is not a scalar multiple of
the first vector, the vectors are linearly independent.
Therefore {{1, 2, 3), (-2, 4, 1)} is a basis for V.
Thus dim(V) = 2.
We know that V is, in fact, a plane through the origin.

89. Ch04_89
Theorem 4.12
(a) The origin is a subspace of R3. The dimension of this
subspace is defined to be zero.
(b) The one-dimensional subspaces of R3 are lines through the
origin.
(c) The two-dimensional subspaces of R3 are planes through the
origin.
Figure 4.16 One and two-dimensional subspaces of R3

90. Ch04_90
Proof
(a) Let V be the set {(0, 0, 0)}, consisting of a single elements,
the zero vector of R3. Let c be the arbitrary scalar. Since
(0, 0, 0) + (0, 0, 0) = (0, 0, 0) and c(0, 0, 0) = (0, 0, 0)
V is closed under addition and scalar multiplication. It is thus
a subspace of R3. The dimension of this subspaces is defined
to be zero.
(b) Let v be a basis for a one-dimensional subspace V of R3.
Every vector in V is thus of the form cv, for some scalar c. We
know that these vectors form a line through the origin.
(c) Let {v1, v2}be a basis for a two-dimensional subspace V of R3.
Every vector in V is of the form c1v1 + c2v2. V is thus a plane
through the origin.

91. Ch04_91
Theorem 4.13
Let {v1, …, vn} be a basis for a vector space V. Then each vector
in V can be expressed uniquely as a linear combination of these
vectors.
Proof
Let v be a vector in V. Since {v1, …, vn} is a basis, we can
express v as a linear combination of these vectors. Suppose we
can write
n
n
n
n b
b
a
a v
v
v
v
v
v 




 
 1
1
1
1 and
Then
giving
n
n
n
n b
b
a
a v
v
v
v 



 
 1
1
1
1
0
v
v 
-


- n
n
n b
a
b
a )
(
)
( 1
1
1 
Since {v1, …, vn} is a basis, the vectors v1, …, vn are linearly
independent. Thus (a1 – b1) = 0, …, (an – bn) = 0, implying that
a1 = b1, …, an = bn. There is thus only one way of expressing v
as a linear combination of the basis.

92. Ch04_92
Theorem 4.14
Let V be a vector space of dimension n.
(a) If S = {v1, …, vn} is a set of n linearly independent vectors
in V, then S is a basis for V.
(b) If S = {v1, …, vn} is a set of n vectors V that spans V, then S
is a basis for V.
Let V be a vector space, S = {v1, …, vn} is a set of vectors in V.
(a) dim(V) = |S|.
(b) S is a linearly independent set.
(c) S spans V.
S is a basis of V.

93. Ch04_93
Example 4
Prove that the set B={(1, 3, -1), (2, 1, 0), (4, 2, 1)} is a basis for R3.
Solution
Since dim(R3)=|B|=3. It suffices to show that this set is linearly
independent or it spans R3.
Let us check for linear independence. Suppose
)
0
,
0
,
0
(
)
1
,
2
,
4
(
)
0
,
1
,
2
(
)
1
,
3
,
1
( 3
2
1 


- c
c
c
This identity leads to the system of equations
This system has the unique solution c1 = 0, c2 = 0, c3 = 0.
Thus the vectors are linearly independent.
The set {(1, 3, -1), (2, 1, 0), (4, 2, 1)} is therefore a basis for R3.
0
0
2
3
0
4
2
3
1
3
2
1
3
2
1


-






c
c
c
c
c
c
c
c

94. Ch04_94
Theorem 4.15
Let V be a vector space of dimension n. Let {v1, …, vm} be a set
of m linearly independent vectors in V, where m < n.
Then there exist vectors vm+1, …, vn such that
{v1, …, vm, vm+1, …, vn } is a basis of V.

95. Ch04_95
Example 5
State (with a brief explanation) whether the following statements
are true or false.
(a) The vectors (1, 2), (-1, 3), (5, 2) are linearly dependent in R2.
(b) The vectors (1, 0, 0), (0, 2, 0), (1, 2, 0) span R3.
(c) {(1, 0, 2), (0, 1, -3)} is a basis for the subspace of R3 consisting
of vectors of the form (a, b, 2a -3b).
(d) Any set of two vectors can be used to generate a two-
dimensional subspace of R3.
Solution
(a) True: The dimension of R2 is two. Thus any three vectors are
linearly dependent.
(b) False: The three vectors are linearly dependent. Thus they
cannot span a three-dimensional space.

96. Ch04_96
(c) True: The vectors span the subspace since
(a, b, 2a -3b) = a(1, 0, 2) + b(0, 1, -3)
The vectors are also linearly independent since they are not
colinear.
(d) False: The two vectors must be linearly independent.

97. Homework
Exercise set 4.4 pages 226-227:
1, 3, 5, 11, 13, 15, 17, 20.
Ch04_97