This document discusses algorithms and techniques for computing the Stanley depth of monomial ideals. It begins by introducing some key concepts such as squarefree monomial ideals and the Stanley depth. It then describes an approach for computing the Stanley depth of a squarefree monomial ideal by partitioning the collection of subsets of variables into non-colliding intervals. The document presents pseudocode for expanding an interval into its constituent sets. It also references several related papers on algorithms for computing Stanley depth and bounds on the Stanley depth of certain classes of monomial ideals.

1. Aswasan Joshi
Stanley Depth of Monomial Ideals:
A Computational Investigation

2. 3x 5−πx 3+3x+ √7

3. Coefficients
3x 5−πx 3+3x+ √7

4. ½
⅓
-⅔
¼
¾
-⅕
⅖
⅗
⅘
⅙
⅚
⅛
-⅜
⅝
½
⅕
⅘
⅓
⅖
⅘
½
⅜
⅝
-⅜
⅝ ⅘
⅔
-⅘
⅜
½
⅓
½
⅓
⅘
-⅕
-⅘
-⅗
Field
Addition, Subtraction, Multiplication & Division
by nonzero numbers in the collection are all defined
-⅝
-⅘

5. ½
⅓
-⅔
¼
¾
-⅕
⅖
⅗
⅘
⅙
⅛
-⅜
⅝
½
⅕
⅘
⅓
⅖
⅘
½
⅜
⅝
-⅜
⅝ ⅘
⅔
-⅘
⅜
½
⅓
½
⅓
⅘
-⅕
-⅘
-⅗
Field
Addition, Subtraction, Multiplication & Division
by nonzero numbers in the collection are all defined
-⅝
-⅘
✓
✗
Rational, Real
Complex numbers Integers⅚

6. If K is a field,
the polynomial ring in n variables,
denoted K [ x1,...,xn ],
consists of all polynomials
where the coefficients come
from the field K
and the variables x1,x2,...,xn
are all allowed to appear.

7. K is the rational numbers
½x1
3x2 −3x3 +7x1
&
⅝x1
100 −5x3 +6
examples of polynomials in
K [x1,x2,x3]

8. Squarefree monomial ideals
• A monomial is called
squarefree if each ai is 0 or 1.
✓ x5x8x9 ✗ x5
4x8
2x9
• A monomial ideal is called squarefree if it
is generated by squarefree monomials.
Stanley Depth
!!
!!
!!
!!
⋯!!!
!!

9. Source: Richard P. Stanley

10. How to compute the Stanley depth of a
monomial ideal
HERZOG, J., VLADOIU, M., AND ZHENG, X
Journal of Algebra
11/2009
• Possible to compute the Stanley depth of a
squarefree monomial ideal using only
techniques from discrete mathematics
• It is enough to look at some of the subsets of
{ x1, ..., xn }, which is equivalent to considering
subsets of {1, 2, ..., n}

11. Our goal is then to partition this
collection C of sets into intervals
that do not collide and cover the
whole poset.
1 2 3 4
12 13 23 14 24 34
123 124 134 234
1234
n = 4
nonempty subsets

12. If A and B are subsets of {1, 2, . . . , n},
the interval [A, B] contains every set T such that
A is a subset of T and T is a subset of B.
(We call B the upper bound of the interval.)
[ {1, 2}, {1, 2, 4, 6} ]
{1, 2}, {1, 2, 4}, {1, 2, 6}, {1, 2, 4, 6}
{1, 2, 5} and {2, 4, 6} is not in this interval

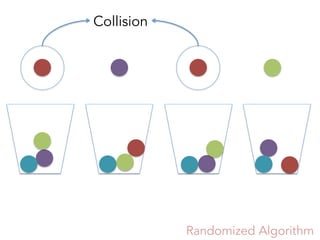
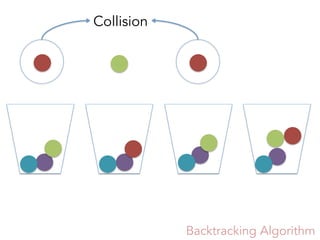
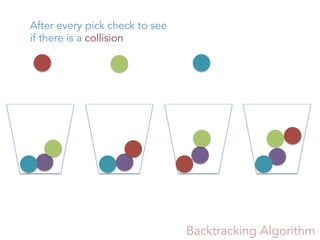
13. Two intervals collide if they have
at least a set in common.
[{1, 6}, {1, 6, 2, 3}] [{1, 3}, {1, 3, 6, 9}]
{1, 3, 6}
Collision
{1, 6}
{1,6,2}
{1, 6, 2, 3}
{1, 3} {1,3,9}
{1, 3, 6, 9}

14. Our goal is then to partition this
collection C of sets into intervals
that do not collide and cover the
whole poset.
1 2 3 4
12 13 23 14 24 34
123 124 134 234
1234
n = 4
nonempty subsets

15. n = 4
nonempty subsets
1 2 3
12 3123
123
4
14 24 34
124 134 234
1234

16. sdepth!! =!max
!
!!!sdepth!!
!!!!!!!!!!!!!!!!!!!=!max
!
min
!,!!!! ∈!
|!|
P – Poset
Q – Partition

17. Interval partitions and Stanley depth
BIRO
́
, CS., HOWARD, D. M., KELLER, M. T.,
TROTTER, W. T., AND YOUNG, S. J.
J. Combin. Theory Ser. A
5/2010
For the case where all nonempty subsets of
{1,2,...,n} are considered, it is possible to find a
partition in which every interval’s upper bound
has size at least n/2.

18. What happens for
all subsets of {1, 2,…, n}
of size at least 2?
sdepth!! = ⌈! + 4
3
⌉!
On the Stanley depth of squarefree Veronese Ideals.
KELLER, M. T., SHEN, Y.-H., STREIB, N., AND YOUNG, S. J.
J. Alg. Combin. (2011)

19. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}

20. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{ }
{3}
{4}
{6}
{7}
{8}
{3, 4}
{3, 6}
{3, 7}
{3, 8}
{4, 6}
{4, 7}
{4, 8}
{6, 7}
{6, 8}
{7, 8}
{3, 4, 6}
{3, 4, 7}
{3, 4, 8}
{3, 6, 7}
{3, 6, 8}
{3, 7, 8}
{4, 6, 7}
{4, 6, 8}
{4, 7, 8}
{6, 7, 8}
{3, 4, 6, 7}
{3, 4, 6, 8}
{3, 4, 7, 8}
{3, 6, 7, 8}
{4, 6, 7, 8}
{3,4,6,7,8}
Powerset of {3, 4, 6, 7, 8}

21. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{ }
{3}
{4}
{6}
{7}
{8}
{3, 4}
{3, 6}
{3, 7}
{3, 8}
{4, 6}
{4, 7}
{4, 8}
{6, 7}
{6, 8}
{7, 8}
{3, 4, 6}
{3, 4, 7}
{3, 4, 8}
{3, 6, 7}
{3, 6, 8}
{3, 7, 8}
{4, 6, 7}
{4, 6, 8}
{4, 7, 8}
{6, 7, 8}
{3, 4, 6, 7}
{3, 4, 6, 8}
{3, 4, 7, 8}
{3, 6, 7, 8}
{4, 6, 7, 8}
{3,4,6,7,8}
Powerset of {3, 4, 6, 7, 8}

22. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A

23. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A

24. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A

25. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4,
7,
8}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A
{3,
4,
8,
6}

26. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4,
7,
8}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A
{3,
4,
8,
6}
{3,
4,
8,
7}

27. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4,
7,
8}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A
{3,
4,
8,
6}
{3,
4,
8,
7}

28. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4,
7,
8}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A
{3,
4,
8,
6}
{3,
4,
8,
7}
{3,
4,
6,
7,
8}
B

29. expand_interval
Input: [{3, 4}, {3, 4, 6, 7, 8}]
Output: {{3,4}, {3,4,6}, {3,4,7}, {3,4,8}, {3,4,6,7},
{3,4,6,8}, {3,4,7,8}, {3,4,6,7,8}}
{3,
4,
6,
7}
{3,
4,
6,
8}
{3,
4,
7,
6}
{3,
4,
7,
8}
{3,
4}
{3,
4,
6}
{3,
4,
7}
{3,
4,
8}
A
{3,
4,
8,
6}
{3,
4,
8,
7}
{3,
4,
6,
7,
8}
B

30. find_partition
Input: n = 8
Output: [[[1, 2], [1, 2, 3, 4]], [[2, 3], [2, 3, 4, 5]], [[3, 4], [3, 4,
5, 6]], [[4, 5], [4, 5, 6, 7]], [[5, 6], [5, 6, 7, 8]], [[6, 7], [6, 7, 8, 1]],
[[7, 8], [7, 8, 1, 2]], [[8, 1], [8, 1, 2, 3]], [[1, 3], [1, 3, 4, 5]], [[2, 4],
[2, 4, 5, 6]], [[3, 5], [3, 5, 6, 7]], [[4, 6], [4, 6, 7, 8]], [[5, 7], [5, 7,
8, 1]], [[6, 8], [6, 8, 1, 2]], [[7, 1], [7, 1, 2, 3]], [[8, 2], [8, 2, 3, 4]],
[[1, 4], [1, 4, 5, 6]], [[2, 5], [2, 5, 6, 7]], [[3, 6], [3, 6, 7, 8]], [[4, 7],
[4, 7, 8, 1]], [[5, 8], [5, 8, 1, 2]], [[6, 1], [6, 1, 2, 3]], [[7, 2], [7, 2,
3, 4]], [[8, 3], [8, 3, 4, 5]], [[1, 5], [1, 5, 2, 6]], [[2, 6], [2, 6, 3, 7]],
[[3, 7], [3, 7, 4, 8]], [[4, 8], [4, 8, 5, 1]]]
• No Collision
• Covers the whole Poset

32. Randomized Algorithm

33. Randomized Algorithm
Collision

34. Randomized Algorithm

36. Backtracking Algorithm

37. Backtracking Algorithm
After every pick, check to see
if there is a collision

38. Backtracking Algorithm
Collision

39. Backtracking Algorithm
If there is a collision, pick another ball.

40. Backtracking Algorithm
After every pick check to see
if there is a collision

41. For
n
=
11
6.845 * 10105

42. 1078 – 1082
atoms
in the observable,
known universe

43. For
n
=
14
1.618 * 10245
6.247
*
10238
possible
par<<ons
per
second

44. Ring Diagram to make Intervals
1
2
3
4
5
6
7
8
[{1,2},{1,2,3,4}]
[A,
B]
n = 8
=
A
+
=
B

45. 1
2
3
4
5
6
7
8
A single rotation
clockwise
n = 8
[{2,3},{2,3,4,5}]

47. ring_to_interval
Input: [1,1,2,2,0,0,0,0]
Output: [[[1, 2], [1, 2, 3, 4]], [[2, 3], [2, 3, 4, 5]], [[3, 4],
[3, 4, 5, 6]], [[4, 5], [4, 5, 6, 7]], [[5, 6], [5, 6, 7, 8]],
[[6, 7], [6, 7, 8, 1]], [[7, 8], [7, 8, 1, 2]], [[8, 1],
[8, 1, 2,3]]]
1
1
2
2
0
0
0
0
1
2
3
4
5
6
7
8
n = 8

48. n = 8
1 - 2 config. 1 - 3 config.
1 - 4 config. 1 - 5 config.

49. n = 14
1 - 2 config. 1 – 3 config.
1 - 4 config. 1 - 5 config. 1 - 6 config.
1 - 7 config. 1 - 8 config.

50. Acknowledgments
• Professor Mitchel T. Keller
• Summer Research Scholars Program
• W&L Mathematics Department