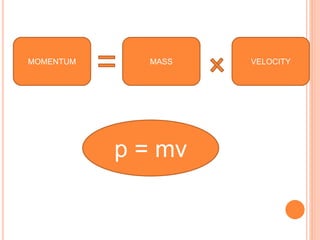
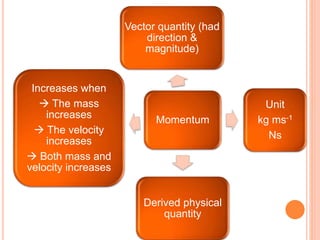
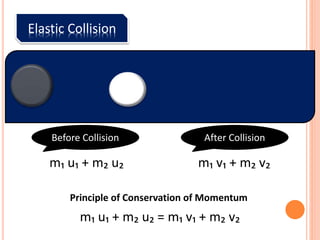
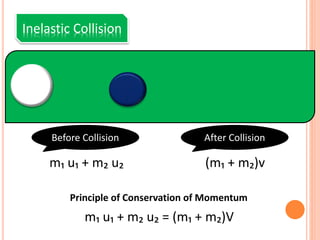
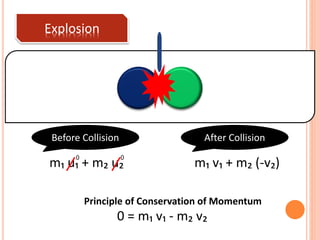
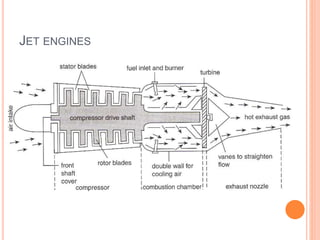
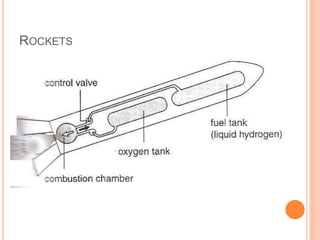
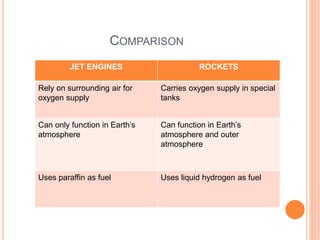
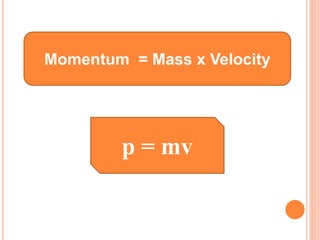
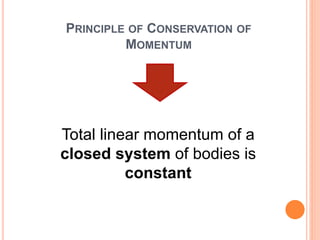
The document discusses linear momentum, the principle of conservation of momentum, and its applications. It defines momentum as the product of mass and velocity (p=mv) and explains that momentum is a vector quantity. The principle of conservation of momentum states that the total momentum of an isolated system remains constant. Elastic collisions result in bodies separating after collision while maintaining the total momentum, inelastic collisions result in bodies sticking together, and explosions involve contact before and separation after. Examples demonstrate applying the principle to calculate velocities and momentum in collisions and explosions.

1. LINEAR
MOMENTUM

2. CONCEPT OF LINEAR
MOMENTUM

3. MOMENTUM VELOCITYMASS
p = mv

4. Momentum
Vector quantity (had
direction &
magnitude)
Unit
kg ms-1
Ns
Derived physical
quantity
Increases when
 The mass
increases
 The velocity
increases
 Both mass and
velocity increases

5. CONSERVATION OF
MOMENTUM

6. PRINCIPLE OF CONSERVATION OF
MOMENTUM
Total linear momentum of a
closed system of bodies is
constant

7. JUST PUT IT THIS WAY…
Total momentum
before and after
collision is conserved
if no external forces
act on the system
Total momentum before collision
= Total momentum after collision

8. ELASTIC COLLISION
 The colliding objects move separately after collision
INELASTIC COLLISION
EXPLOSION
 The colliding objects move together after collision
 The objects involved are in contact with each other
before explosion and are separated after the
explosion

9. Elastic Collision
Before Collision After Collision
m₁ u₁ + m₂ u₂ m₁ v₁ + m₂ v₂
Principle of Conservation of Momentum
m₁ u₁ + m₂ u₂ = m₁ v₁ + m₂ v₂

10. Inelastic Collision
Before Collision After Collision
m₁ u₁ + m₂ u₂ (m₁ + m₂)v
m₁ u₁ + m₂ u₂ = (m₁ + m₂)V
Principle of Conservation of Momentum

11. Explosion
Before Collision After Collision
m₁ u₁ + m₂ u₂ m₁ v₁ + m₂ (-v₂)
Principle of Conservation of Momentum
0 = m₁ v₁ - m₂ v₂
0 0

12. Elastic Inelastic Explosion
m₁ u₁ + m₂ u₂ = m₁ v₁ +
m₂ v₂
m₁ u₁ + m₂ u₂ = (m₁ +
m₂)V
0 = m₁ v₁ - m₂ v₂
Momentum is conserved

13. APPLICATION: THE PRINCIPLE OF
CONSERVATION OF MOMENTUM

14. JET ENGINES

15. ROCKETS

16. COMPARISON
JET ENGINES ROCKETS
Rely on surrounding air for
oxygen supply
Carries oxygen supply in special
tanks
Can only function in Earth’s
atmosphere
Can function in Earth’s
atmosphere and outer
atmosphere
Uses paraffin as fuel Uses liquid hydrogen as fuel

17. APPLICATION OF IDEA

18. Car A of mass 100 kg moving at 20 m sˉ¹ collides with
car B of mass 1 200 kg moving at 10 ms ˉ¹ in the same
direction. If car B is pushed forwards at 15 ms ˉ¹ by the
impact, find the;
(a) Velocity of the car A immediately after the
collision.
(b) What type is this collision? Why?

19.  (100 x 20) + (1200 x 10) = (100 x V1) + (1200 x 15)
 14000 = 100V1 + 18000
 V1 = - 40ms-1
 Elastic collision because both car are moving in
opposite direction
M₁ U₁ + M₂ U₂ = M₁ V₁ + M₂ V₂
Principle of Conservation of Momentum

20. A trolley of mass 4kg moves at 3 m sˉ¹ and collides
with a trolley of mass 2kg which is moving in the
opposite direction at 1 ms ˉ¹. After the collision, both
trolley move together with the same velocity.
(a) What is the final velocity of both trolleys?
(b) What type is this collision? Why?

21.  (4 x 3) + (2 x -1) = (4 + 2) V
 12 + (-2) = 6V
 V = 1.7 ms-1
 Inelastic collision because both trolley are moving
together
Principle of Conservation of Momentum
m₁ u₁ + m₂ u₂ = (m₁ + m₂)V

22. A man fires a pistol which has a mass of 1.5 kg. if the
mass of the bullet is 10 g and it reaches a velocity of
300 m sˉ¹ after shooting. What is the recoil velocity of
the pistol?

23.  0 = (0.01x 300) - 1.5V2
 0 = 3 - 1.5V2
 V2 = 2 ms-1
Principle of Conservation of Momentum
0 = m₁ v₁ - m₂ v₂

24. In a football game, a player of mass 70 kg
is moving with velocity of 4 msˉ¹ and
another player of mass 76 kg is moving with
3 msˉ¹ towards each other. Calculate the
total initial momentum of both players.

25.  Total initial momentum = (70 x 4) + (76 x 3)
 Total initial momentum = 280 + 138
 Total initial momentum = 418 kg ms-1
Total initial momentum = m₁ v₁ + m₂ v₂

27.  Total initial momentum = (80x 6) + (40 x 0)
 Total initial momentum = 480 + 0
 Total initial momentum = 480 kg ms-1
Total initial momentum = m₁ v₁ + m₂ v₂

28. SUMMARY

29. Momentum = Mass x Velocity
p = mv

30. PRINCIPLE OF CONSERVATION OF
MOMENTUM
Total linear momentum of a
closed system of bodies is
constant

31. Elastic Inelastic Explosion
Both bodies will separate
after collision
Both bodies will move
together after collision
Two or more bodies in
contact will be separated
after the collision
m₁ u₁ + m₂ u₂ = m₁ v₁ +
m₂ v₂
m₁ u₁ + m₂ u₂ = (m₁ +
m₂)V
0 = m₁ v₁ - m₂ v₂
Momentum is conserved
DIFFERENCES AND SIMILARITIES