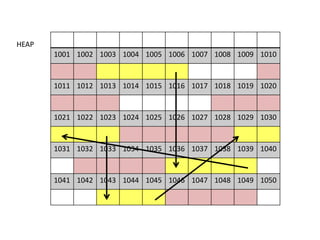
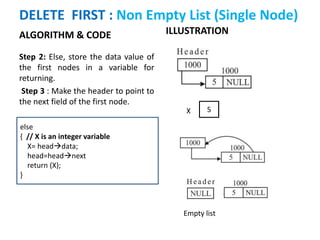
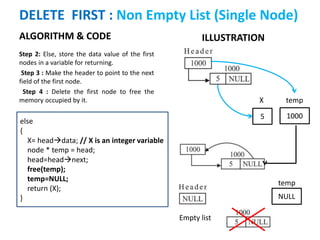
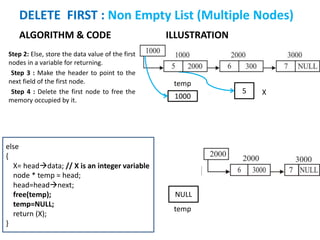
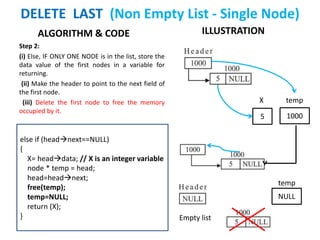
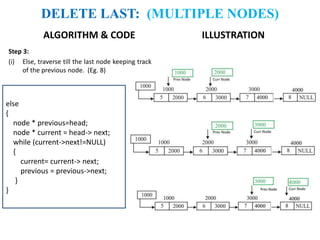
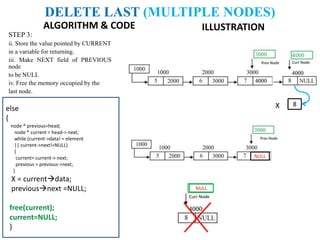
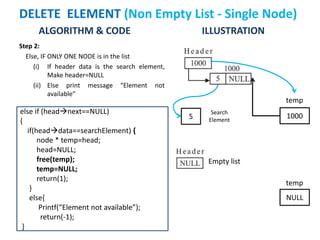
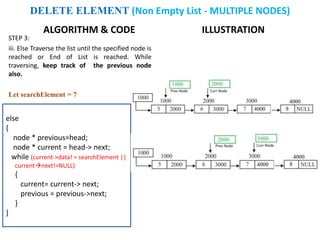
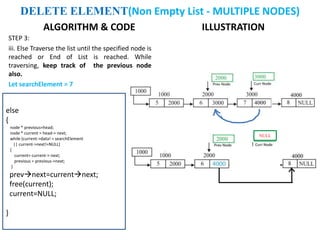
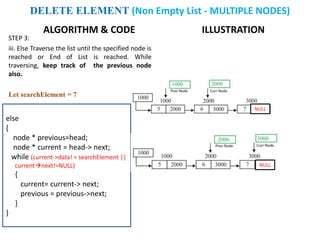
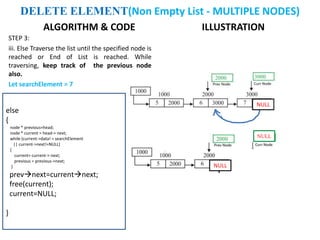
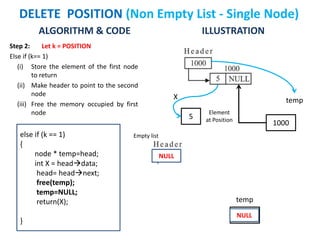
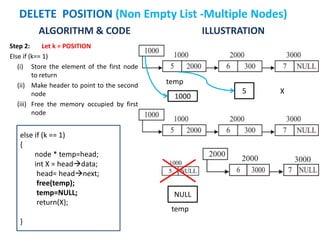
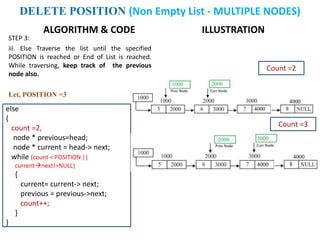
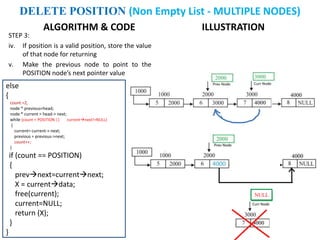
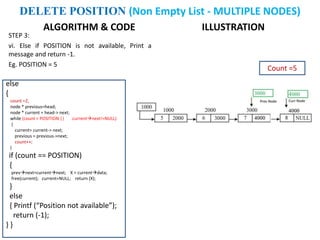
The document discusses various deletion operations on singly linked lists. It provides algorithms and code snippets for deleting the first element, last element, a given element, and an element at a given position in a singly linked list. The algorithms handle both empty lists and non-empty lists with single and multiple nodes. Key steps include checking for empty lists, traversing the list to find the required element or position while tracking the previous node, and updating pointers after deleting the node.

1. DATA STRUCTURES
Dr. P. Subathra
Professor
Dept. of Information Technology
KAMARAJ College of Engineering & Technology

2. CS8391 – DATA STRUCTURES
ONLINE CLASSES – CLASS NO. 4
21.08.2020
(10:00 AM – 11:00 AM
&
11:30 AM – 12:30 PM)

3. UNIT 1
SINGLY LINKED LIST

4. DELETION OPERATIONS

5. HEAP
1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
LOOK CLOSER……

6. HEAP
1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
LOOK CLOSER……

7. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

8. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

9. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

10. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

11. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

12. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
free()
HEAP

13. Operations on a Singly Linked List
• Creating a new list
• Insertion
- at the beginning
- at the end
- after and element
- before an element
• Deletion
- at the beginning
- at the end
- a given element
- at a position
• Display
• Search Element
• Reverse List
• Sort List
• Find Duplicates
• ………………

14. DELETE FIRST

15. ALGORITHM
Step 1 : Check if the list is empty,
if so, display a message and exit
Step 2: Else, store the data value
of the first nodes in a variable for
returning.
Step 3 : Make the header to point
to the next field of the first node.
Step 4 : Delete the first node to
free the memory occupied by it.
SAME ALGORITHM WORKS
• Case 1
– Delete from an Empty List
• Case 2
– Delete from a Non Empty List
DELETE FIRST

16. ALGORITHM & CODE
Step 1 : Check if the list is
empty, if so, display a message
and exit
ILLUSTRATION
DELETE FIRST (Empty List)
If (head == NULL)
{
printf(“Empty List, ignore the return
value”);
return (-999);
}

17. ALGORITHM & CODE
Step 2: Else, store the data value of
the first nodes in a variable for
returning.
Step 3 : Make the header to point to
the next field of the first node.
ILLUSTRATION
DELETE FIRST : Non Empty List (Single Node)
else
{ // X is an integer variable
X= headdata;
head=headnext
return (X);
}
Empty list
5X

18. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP

19. ALGORITHM & CODE
Step 2: Else, store the data value of the first
nodes in a variable for returning.
Step 3 : Make the header to point to the next
field of the first node.
Step 4 : Delete the first node to free the
memory occupied by it.
ILLUSTRATION
else
{
X= headdata; // X is an integer variable
node * temp = head;
head=headnext;
free(temp);
temp=NULL;
return (X);
}
Empty list
5
X
temp
1000
NULL
temp
DELETE FIRST : Non Empty List (Single Node)

20. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP
1036
temp

21. 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
HEAP
1036
temp
NULL

22. ALGORITHM & CODE
Step 2: Else, store the data value of the first
nodes in a variable for returning.
Step 3 : Make the header to point to the
next field of the first node.
Step 4 : Delete the first node to free the
memory occupied by it.
ILLUSTRATION
DELETE FIRST : Non Empty List (Multiple Nodes)
else
{
X= headdata; // X is an integer variable
node * temp = head;
head=headnext;
free(temp);
temp=NULL;
return (X);
}
5 X
temp
1000
NULL
temp

23. DELETE LAST

24. DELETE LAST
Step 1 : Check if the list is empty,
if so, display a message and exit
Step 2: Else, if only one node
available in the list, store the
data value of that nodes in a
variable for returning.
Step 3 : Make the header NULL
Step 4 : Delete the first node to
free the memory occupied by it.
SAME ALGORITHM WORKS
• Case 1
– Delete an Empty List
• Case 2
– Delete from a Non Empty List
Operations on a Singly Linked List

25. ALGORITHM & CODE
Step 1 : Check if the list is
empty, if so, display a message
and exit
ILLUSTRATION
DELETE LAST : Empty List
If (head == NULL)
{
printf(“Empty List, ignore the return
value”);
return (-999);
}

26. ALGORITHM & CODE
Step 2:
(i) Else, IF ONLY ONE NODE is in the list, store the
data value of the first nodes in a variable for
returning.
(ii) Make the header to point to the next field of
the first node.
(iii) Delete the first node to free the memory
occupied by it.
ILLUSTRATION
DELETE LAST (Non Empty List - Single Node)
else if (headnext==NULL)
{
X= headdata; // X is an integer variable
node * temp = head;
head=headnext;
free(temp);
temp=NULL;
return (X);
} Empty list
5
X
temp
1000
NULL
temp

27. ALGORITHM & CODE
Step 3:
(i) Else, traverse till the last node keeping track
of the previous node. (Eg. 8)
ILLUSTRATION
else
{
node * previous=head;
node * current = head-> next;
while (current->next!=NULL)
{
current= current-> next;
previous = previous->next;
}
}
DELETE LAST: (MULTIPLE NODES)

28. ALGORITHM & CODE
STEP 3:
ii. Store the value pointed by CURRENT
in a variable for returning.
iii. Make NEXT field of PREVIOUS
node
to be NULL
iv. Free the memory occupied by the
last node.
ILLUSTRATION
DELETE LAST (MULTIPLE NODES)
else
{
node * previous=head;
node * current = head-> next;
while (current->data! = element
|| current->next!=NULL)
{
current= current-> next;
previous = previous->next;
}
X = currentdata;
previousnext =NULL;
free(current);
current=NULL;
}
8X
NULL
NULL

29. DELETE ELEMENT

30. ALGORITHM & CODE
Step 1 : Check if the list is
empty, if so, display a message
and exit
ILLUSTRATION
DELETE ELEMENT (Empty List)
If (head == NULL)
{
printf(“Empty List, Element not available
ignore the return value”);
return (-1);
}

31. ALGORITHM & CODE
Step 2:
Else, IF ONLY ONE NODE is in the list
(i) If header data is the search element,
Make header=NULL
(ii) Else print message “Element not
available”
ILLUSTRATION
DELETE ELEMENT (Non Empty List - Single Node)
else if (headnext==NULL)
{
if(headdata==searchElement) {
node * temp=head;
head=NULL;
free(temp);
temp=NULL;
return(1);
}
else{
Printf(“Element not available”);
return(-1);
}
Empty list
5
Search
Element
temp
1000
NULL
temp

32. ALGORITHM & CODE
STEP 3:
iii. Else Traverse the list until the specified node is
reached or End of List is reached. While
traversing, keep track of the previous node
also.
Let searchElement = 7
ILLUSTRATION
else
{
node * previous=head;
node * current = head-> next;
while (current->data! = searchElement ||
currentnext!=NULL)
{
current= current-> next;
previous = previous->next;
}
}
DELETE ELEMENT (Non Empty List - MULTIPLE NODES)

33. ALGORITHM & CODE
STEP 3:
iii. Else Traverse the list until the specified node is
reached or End of List is reached. While
traversing, keep track of the previous node
also.
Let searchElement = 7
ILLUSTRATION
else
{
node * previous=head;
node * current = head-> next;
while (current->data! = searchElement
|| current->next!=NULL)
{
current= current-> next;
previous = previous->next;
}
prevnext=currentnext;
free(current);
current=NULL;
}
DELETE ELEMENT(Non Empty List - MULTIPLE NODES)
NULL

34. ALGORITHM & CODE
STEP 3:
iii. Else Traverse the list until the specified node is
reached or End of List is reached. While
traversing, keep track of the previous node
also.
Let searchElement = 7
ILLUSTRATION
else
{
node * previous=head;
node * current = head-> next;
while (current->data! = searchElement ||
currentnext!=NULL)
{
current= current-> next;
previous = previous->next;
}
}
DELETE ELEMENT (Non Empty List - MULTIPLE NODES)
NULL
NULL

35. ALGORITHM & CODE
STEP 3:
iii. Else Traverse the list until the specified node is
reached or End of List is reached. While
traversing, keep track of the previous node
also.
Let searchElement = 7
ILLUSTRATION
else
{
node * previous=head;
node * current = head-> next;
while (current->data! = searchElement
|| current->next!=NULL)
{
current= current-> next;
previous = previous->next;
}
prevnext=currentnext;
free(current);
current=NULL;
}
DELETE ELEMENT(Non Empty List - MULTIPLE NODES)
NULL
NULL
NULL NULL

36. DELETE GIVEN POSITION

37. ALGORITHM & CODE
Step 1 : Check if the list is
empty, if so, display a message
and exit
ILLUSTRATION
DELETE POSITION (Empty List)
If (head == NULL)
{
printf(“Empty List, Element not available
ignore the return value”);
return (-1);
}

38. ALGORITHM & CODE ILLUSTRATION
DELETE POSITION (Non Empty List - Single Node)
else if (k == 1)
{
node * temp=head;
int X = headdata;
head= headnext;
free(temp);
temp=NULL;
return(X);
}
Empty list
5
Element
at Position
1000
tempX
Step 2: Let k = POSITION
Else if (k== 1)
(i) Store the element of the first node
to return
(ii) Make header to point to the second
node
(iii) Free the memory occupied by first
node
1000
temp
NULL
NULL

39. ALGORITHM & CODE
Step 2: Let k = POSITION
Else if (k== 1)
(i) Store the element of the first node
to return
(ii) Make header to point to the second
node
(iii) Free the memory occupied by first
node
ILLUSTRATION
DELETE POSITION (Non Empty List -Multiple Nodes)
else if (k == 1)
{
node * temp=head;
int X = headdata;
head= headnext;
free(temp);
temp=NULL;
return(X);
}
5
1000
X
temp
temp
NULL

40. ALGORITHM & CODE
STEP 3:
iii. Else Traverse the list until the specified
POSITION is reached or End of List is reached.
While traversing, keep track of the previous
node also.
Let, POSITION =3
ILLUSTRATION
else
{
count =2,
node * previous=head;
node * current = head-> next;
while (count < POSITION ||
currentnext!=NULL)
{
current= current-> next;
previous = previous->next;
count++;
}
}
DELETE POSITION (Non Empty List - MULTIPLE NODES)
Count =2
Count =3

41. STEP 3:
iv. If position is a valid position, store the value
of that node for returning
v. Make the previous node to point to the
POSITION node’s next pointer value
ILLUSTRATION
else
{
count =2,
node * previous=head;
node * current = head-> next;
while (count < POSITION || currentnext!=NULL)
{
current= current-> next;
previous = previous->next;
count++;
}
if (count == POSITION)
{
prevnext=currentnext;
X = currentdata;
free(current);
current=NULL;
return (X);
}
}
DELETE POSITION (Non Empty List - MULTIPLE NODES)
NULL
ALGORITHM & CODE

42. STEP 3:
vi. Else if POSITION is not available, Print a
message and return -1.
Eg. POSITION = 5
ILLUSTRATION
else
{
count =2,
node * previous=head;
node * current = head-> next;
while (count < POSITION || currentnext!=NULL)
{
current= current-> next;
previous = previous->next;
count++;
}
if (count == POSITION)
{
prevnext=currentnext; X = currentdata;
free(current); current=NULL; return (X);
}
else
{ Printf (“Position not available”);
return (-1);
} }
DELETE POSITION (Non Empty List - MULTIPLE NODES)
ALGORITHM & CODE
Count =5

43. END OF
DELETION OPERATIONS

44. PRINT THE LIST