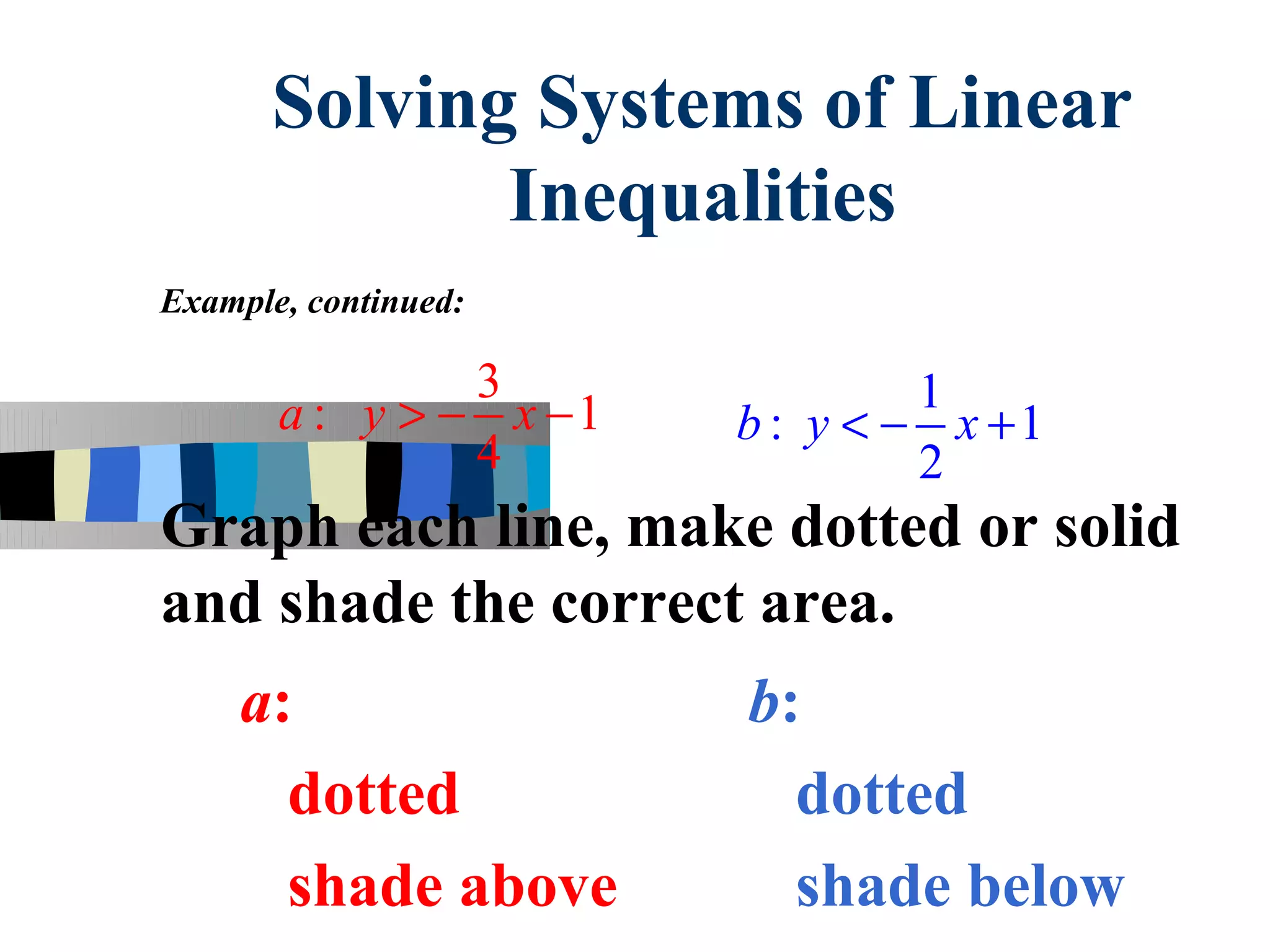
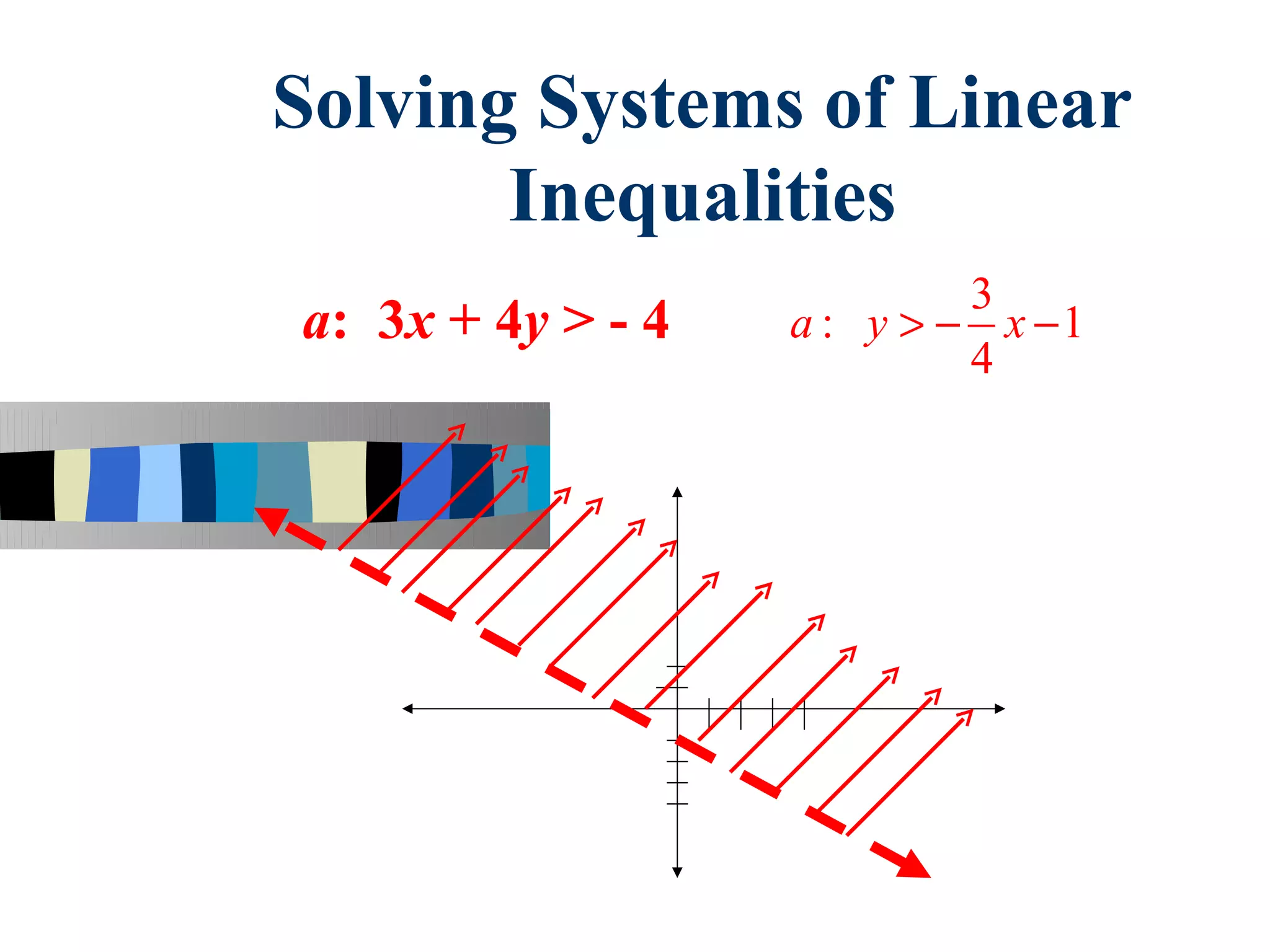
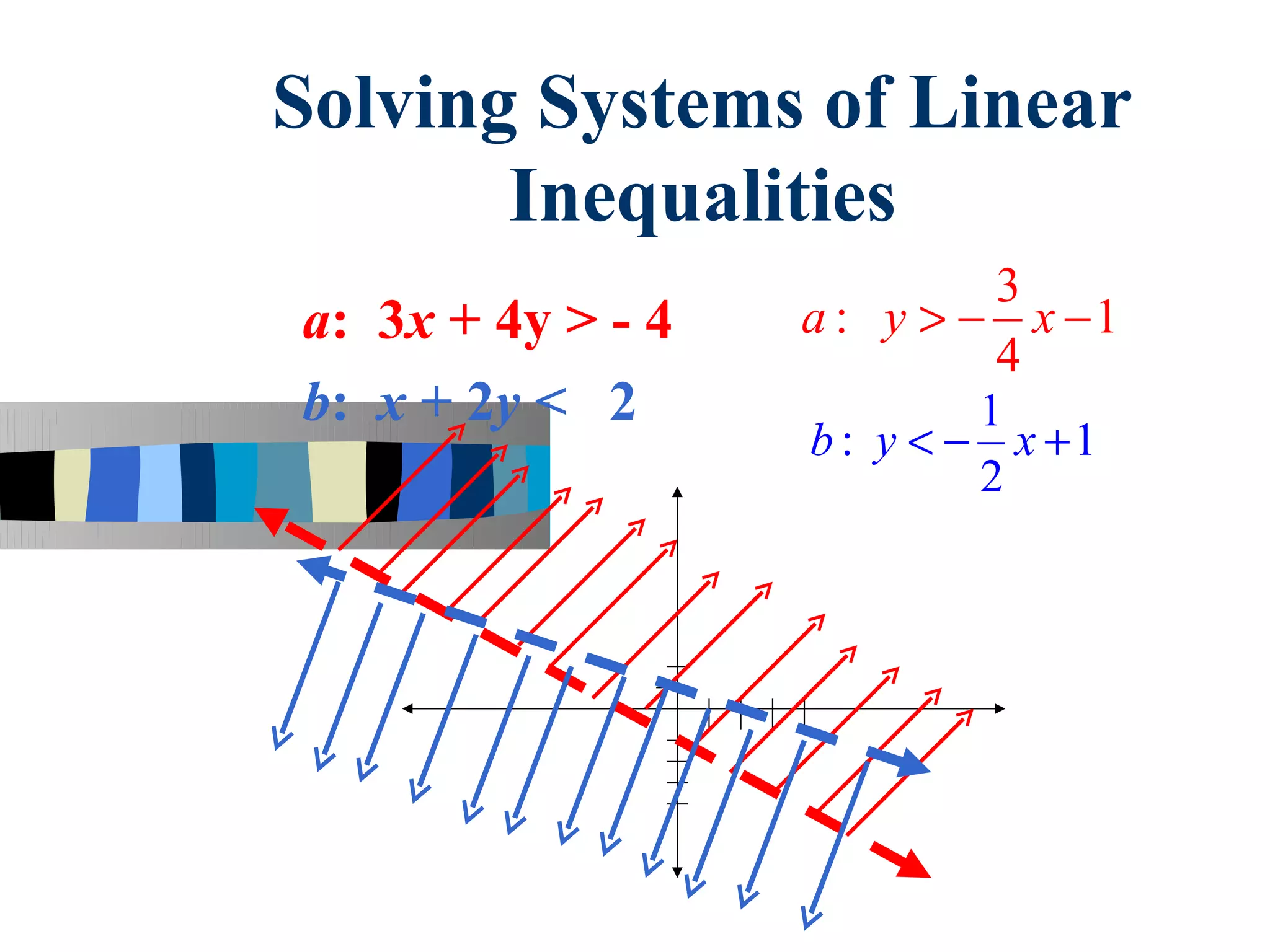
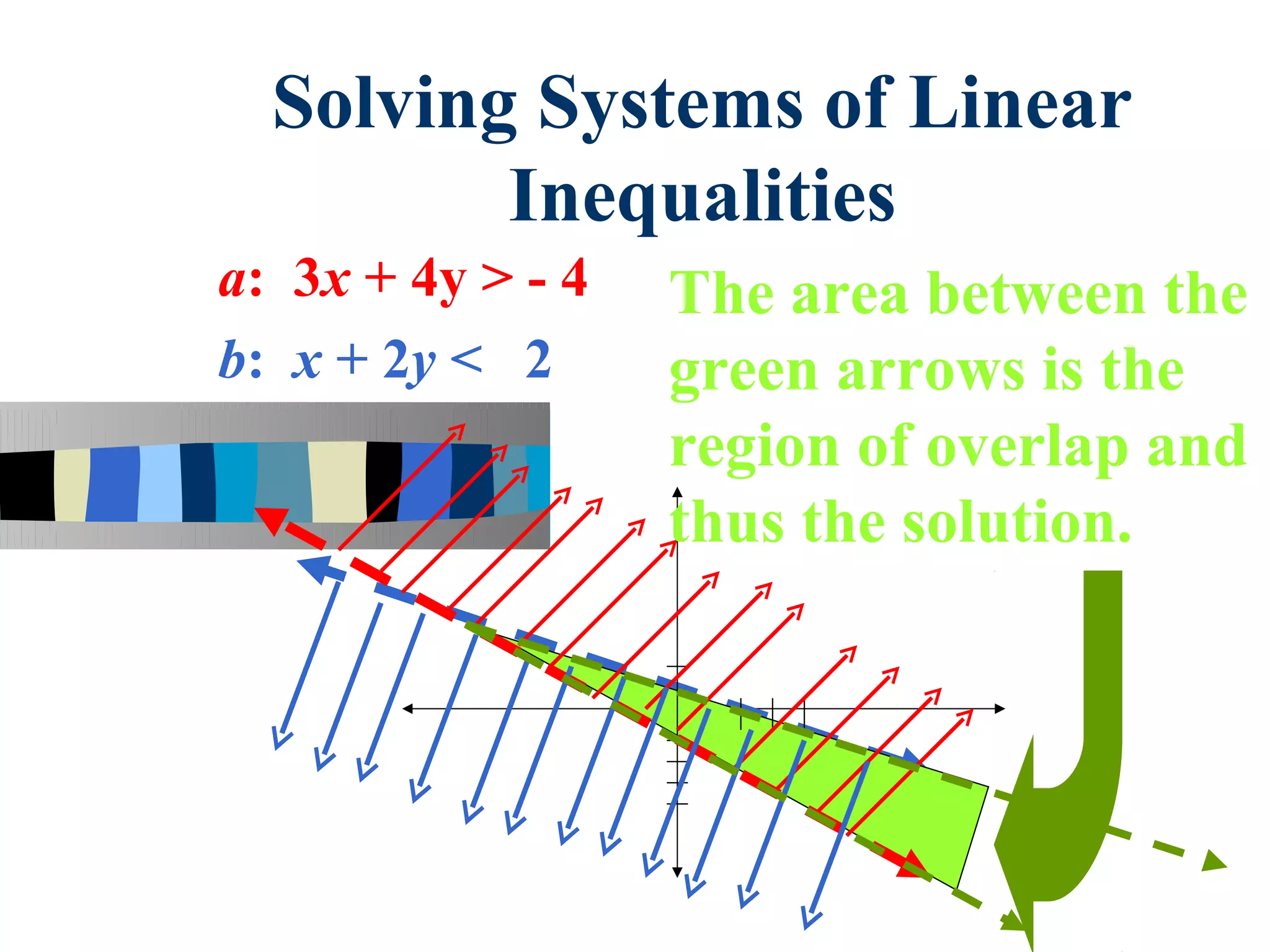
1. Systems of linear inequalities can be solved by graphing the inequalities on a coordinate plane. 2. Each inequality is written in slope-intercept form (y=mx+b) and graphed as either a solid or dotted line. 3. The region representing the solution of the system is found by shading the area of overlap between the graphs based on whether each inequality represents "above or below" the line.

1. SYSTEMS OF LINEAR
INEQUALITIES
Today’s objective:
1. I will graph a system of three or
more linear inequalities.

2. Solving Systems of Linear
Inequalities
1. We show the solution to a system of
linear inequalities by graphing
them.
a) This process is easier if we put the
inequalities into Slope-Intercept
Form, y = mx + b.

3. Solving Systems of Linear
Inequalities
2. Graph the line using the y-intercept
& slope.
a) If the inequality is < or >, make
the lines dotted.
b) If the inequality is < or >, make
the lines solid.

4. Solving Systems of Linear
Inequalities
3. The solution also includes points
not on the line, so you need to
shade the region of the graph:
a) above the line for ‘y >’ or ‘y ≥’.
b) below the line for ‘y <’ or ‘y ≤’.

5. Solving Systems of Linear
Inequalities
Example:
a: 3x + 4y > - 4
b: x + 2y < 2
Put in Slope-Intercept Form:
a) 3x + 4 y > −4 b) x + 2 y < 2
4 y > − 3x − 4 2 y < −x + 2
3 1
y > − x −1 y < − x +1
4 2

6. Solving Systems of Linear
Inequalities
Example, continued:
3 1
a : y > − x −1 b : y < − x +1
4 2
Graph each line, make dotted or solid
and shade the correct area.
a: b:
dotted dotted
shade above shade below

7. Solving Systems of Linear
Inequalities
3
a: 3x + 4y > - 4 a : y > − x −1
4

8. Solving Systems of Linear
Inequalities
3
a: 3x + 4y > - 4 a : y > − x −1
4
b: x + 2y < 2 1
b : y < − x +1
2

9. Solving Systems of Linear
Inequalities
a: 3x + 4y > - 4 The area between the
b: x + 2y < 2 green arrows is the
region of overlap and
thus the solution.