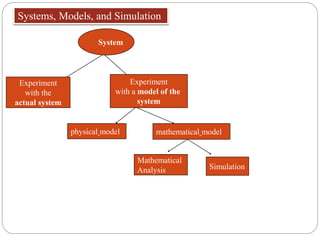
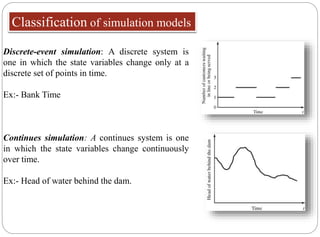
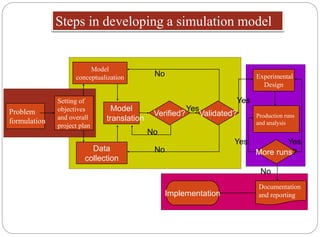
The document discusses system simulation. It defines key terms like system, model, modeling, and simulation. It explains that a simulation experiments with a model of a system rather than the actual system. There are different types of simulations - discrete-event vs continuous, deterministic vs stochastic. Simulation can be done by hand, with spreadsheets, programming languages, or simulation packages. The steps in developing a simulation model are outlined. Advantages include understanding systems without using real-time systems and testing changes. Disadvantages include requiring expertise and being time-consuming. Dimensional analysis using Buckingham's π-theorem is also summarized.

1. System Simulation
Presented by
Amita Gautam
PhD Schollar (FMPE)
Submitted to
Dr. A. K. Verma
Department of Farm Machinery and Power Engineering
SVCAET & Reaserch Station, Faculty of Agril. Engineering
Indira Gandhi Krishi Vishwavidyalaya, Raipur(C.G)
DEPARTMENT OF FARM MACHINERY AND POWER
ENGINEERING
SVCAETRS, FACULTY OF AGRICULTURAL ENGINEERING
INDIRA GANDHI KRISHI VISHWAVIDYALAYA
RAIPUR (CHHATTISGARH)

2. System:- A set of things working together as parts of a mechanism or an
interconnecting network
Examples: A manufacturing system with its machine centres, conveyor belts etc.
Systems, Models, and Simulation
Model:- A model is the small scale replica of the actual structure or machine.
Modeling:- Modeling is the process of representing a model which includes its
construction and working.
Simulation :- Simulation of a system is the operation of a model in terms of time
or space, which helps analyze the performance of an existing
system. The simulation process involves
 Construction of models
Analytical use of models for studying a problem

3. mathematical model
Mathematical
Analysis
physical model
System
Experiment
with the
actual system
Simulation
Experiment
with a model of the
system
Systems, Models, and Simulation

4. Discrete-event simulation: A discrete system is
one in which the state variables change only at a
discrete set of points in time.
Ex:- Bank Time
Continues simulation: A continues system is one
in which the state variables change continuously
over time.
Ex:- Head of water behind the dam.
Classification of simulation models

5. Deterministic: Simulation data will not be probabilistic result will be Constant.
Given input will always produce the same output.
Ex- y= m x+ c
Stochastic: Simulation data will be probabilistic result will be varying.
Randomness affects the behavior of the system.
Ex- Bank with customers and tellers
Dynamic: Dynamic simulation model represent system as they Change over
time.
Ex- Water level in dam
Static: A simulation of a system at one specific time.
Ex-Monte Carlo & steady-state simulations, Estimation of pi.
Stochastic and Deterministic Systems

6.  By hand
 Buffon Needle and Cross Experiments (see Kelton et al.)
 Spreadsheets
 Programming in General Purpose Languages
• Java
 Simulation Languages
 SIMAN
 Simulation Packages
 Arena
HOW TO SIMULATE

7. Problem
formulation
Setting of
objectives
and overall
project plan
Model
conceptualization
Data
collection
Model
translation
Verified?
No
Validated?
No
No Experimental
Design
Production runs
and analysis
More runs?
Documentation
and reporting
No
Implementation
Yes
Yes
Yes
Yes
Steps in developing a simulation model

8.  Easy to understand: Allows to understand how the system really operates without
working on real-time systems.
 Easy to test: Allows to make changes into the system and their effect on the output
without working on real-time systems.
 Easy to upgrade: Allows to determine the system requirements by applying different
configurations.
 Easy to identifying constraints: Allows to perform bottleneck analysis that causes
delay in the work process, information, etc.
 Easy to diagnose problems: Certain systems are so complex that it is not easy to
understand their interaction at a time. However, Modelling & Simulation allows to
understand all the interactions and analyze their effect.
Advantages of modeling & simulation

9. Designing a model is an art which requires domain knowledge, training and
experience.
Operations are performed on the system using random number, hence
difficult to predict the result.
Simulation requires manpower and it is a time-consuming process.
Simulation results are difficult to translate, it requires experts to understand.
Simulation process is expensive.
Disadvantages of modeling & simulation

10. The Buckingham’s π-Method/Theorem in Dimensional Analysis
 If there are n variable (dependent and independent variables) in a dimensionally
homogeneous equation and if these variable contains m fundamental dimensions (such M,
L, T, etc) then the variables are arranged into (n-m) dimensionless terms. These
dimensionless terms are called pi-terms.
Mathematically, if any variable X1, depends on independent variables, X2, X3,
X4,…….Xn; the function equation may be written as
X1 = f(X2, X3, X4,…….Xn)
Eqn. can also be written as
f1(X2, X3, X4,…….Xn) = 0
According to Buckingham’s π-Theorem (n-m) dimension pi term can be formed
f1(π 1,π2, π3……..πn-m) = 0

11. Than it is written in π-term . In which number of π-term is equal to (n-m). Hence eqn.
becomes as
Let X2, X3, X4 are the repeating variable if m = 3
Then pi term can be written as
a1 b1 c1
π 1 = X2. X3. X4 . X1
a2 b2 c2
π 2 = X2. X3. X4 . X5
an-m bn-m cm
π n-m = X2. X3. X4 . Xn
Each equation is solved by principle of homogeneity. And finale answer of pi is obtained .

15. Thank you