The document provides a comprehensive overview of various estimation techniques in control systems, specifically focusing on different types of Kalman filters and their applications. It details the history and development of these methods, highlighting significant contributions by key figures such as Gauss and Kolmogorov. Additionally, it discusses properties of estimators and optimal parameter estimation processes in linear stationary systems.

1. 1
Estimators
SOLO HERMELIN
Updated: 22.02.09
17.06.14
http://www.solohermelin.com

2. 2
EstimatorsSOLO
Table of Content
Summary of Discrete Case Kalman Filter
Extended Kalman Filter
Uscented Kalman Filter
Kalman Filter Discrete Case & Colored Measurement Noise
Parameter Estimation
History
Optimal Parameter Estimate
Optimal Weighted Last-Square Estimate
Recursive Weighted Least Square Estimate (RWLS)
Markov Estimate
Maximum Likelihood Estimate (MLE)
Bayesian Maximum Likelihood Estimate
(Maximum Aposterior – MAP Estimate)
The Cramér-Rao Lower Bound on the Variance of the Estimator
Kalman Filter Discrete Case
Properties of the Discrete Kalman Filter
( ) ( ){ } 01|1~1|1ˆ =++++ kkxkkxE T
(1)
(2) Innovation =White Noise for Kalman Filter Gain

3. EstimatorsSOLO
Table of Content (continue – 1)
Optimal State Estimation in Linear Stationary Systems
Kalman Filter Continuous Time Case
Applications
Multi-sensor Estimate
Target Acceleration Models
Kalman Filter for Filtering Position and Velocity Measurements
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model
Optimal Filtering
Continuous Filter-Smoother Algorithms
References
End of Estimation Presentation
Review of Probability
Random Variables
Matrices
Inner Product
Signals

4. 4
Estimators
v
( )vxh , z
x
SOLO
Estimate parameters x of a given system, by using measurements z corrupted by noise v.
Parameter is a quantity (scalar or vector-valued) that is
usually assumed to be time-invariant. If the parameter
does change with time, it is designed as a time-varying
parameter, but its time variation is assumed slow relative
to system states.
The estimation is performed on different
measurements j = 1,…,k that provide different results
z (j) because of the random variables (noises) v (j)
( ) ( )( ) kjjvxjhjz ,,1,, ==
We define the observation (information) vector as: ( ) ( ){ } ( ){ }k
j
Tk
jzkzzZ 1
1: =
== 
We want to find the estimation of x, given the measurements Zk
:
( ) ( )k
Zkxkx ,ˆˆ =
Assuming that the parameters x are observable (defined later)
from the measurement, and knowledge of the system h (x,ν) the
estimation of x will be done in some sense.
Parameter Estimation

5. 5
Estimators
v
( )vxh , z
x
SOLO
Desirable Properties of Estimators.
( ){ } ( ){ } ( )kxZkxEkxE k
== ,ˆˆ
Unbiased Estimator1
Consistent or Convergent Estimator2
( ) ( )[ ] ( ) ( )[ ]{ } 00ˆˆProblim =>>−−
∞→
εkxkxkxkx
T
k
( ) ( )[ ] ( ) ( )[ ]{ } ( ) ( )[ ] ( ) ( )[ ]{ } KkforkxkxkxkxEkxkxkxkxE
TT
>−−≤−− γγ ˆˆˆˆ
Efficient or Assymptotic Efficient Estimator if for All Unbiased Estimators3 ( )( )kxγγ ˆ
Sufficient Estimator if it contains all the information in the set of observed values
regarding the parameter to be observed.
4 k
Z
( )kx
Table of Content

6. 6
EstimatorsSOLO
History
The Linear Estimation Theory is credited o Gauss, who, in 1798, at
age of 18, invented the method of Least Square.
On January 1st, 1801, the Italian astronomer Giuseppe Piazzi had
discovered the asteroid Ceres and had been able to track its path
for 40 days before it was lost in the glare of the sun. Based on this
data, it was desired to determine the location of Ceres after it
emerged from behind the sun without solving the complicated
Kepler’s nonlinear equations of planetary motion. The only
predictions that successfully allowed the German astronomer
Franz Xaver von Zach to relocate Ceres on 7 December 1801,
were those performed by the 24-year-old Gauss using least-
squares analysis.
However, Gauss did not publish the method until 1809, when it
appeared in volume two of his work on celestial mechanics,
“Theoria Motus Corporum Coelestium in sectionibus conicis
solem ambientium”.
Giuseppe Piazzi
1746 - 1826
Franz Xaver von Zach
1754 - 1832
Gauss' potrait published
in Astronomische
Nachrichten 1828
Johann Carl Friedrich
Gauss
1777 - 1855

7. 7
"In this work Gauss systematically
developed the method of orbit calculation
from three observations he had devised in
1801 to locate the planetoid Ceres, the
earliest discovered of the 'asteroids,'
which had been spotted and lost by G.
Piazzi in January 1801. Gauss predicted
where the planetoid would be found next,
using improved numerical methods based
on least squares, and a more accurate
orbit theory based on the ellipse rather
than the usual circular approximation.
Gauss's calculations, completed in 1801,
enabled the astronomer W. M. Olbers to
find Ceres in the predicted position, a
remarkable feat that cemented Gauss's
reputation as a mathematical and
scientific genius" (Norman 879).
http://www.19thcenturyshop.com/apps/catalogitem?id=84#
Theoria motus corporum coelestium (1809)

8. 8
Sketch of the orbits of Ceres and Pallas, by Gauss
http://www.math.rutgers.edu/~cherlin/History/Papers1999/weiss.html

9. 9
EstimatorsSOLO
History
Legendre published a book on determining the orbits of comets
in 1806. His method involved three observations taken at equal
intervals and he assumed that the comet followed a parabolic
path so that he ended up with more equations than there were
unknowns. He applied his methods to the data known for two
comets. In an appendix Legendre gave the least squares method
of fitting a curve to the data available. However, Gauss published
his version of the least squares method in 1809 and, while
acknowledging that it appeared in Legendre's book, Gauss still
claimed priority for himself. This greatly hurt Legendre who
fought for many years to have his priority recognized.
Adrien-Marie Legendre
1752 - 1833
The idea of least-squares analysis was independently formulated
by the Frenchman Adrien-Marie Legendre in 1805 and the
american Robert Adrain in 1808.
Robert Adrain
1775 - 1843
Legendre, A.M. “Nouvelles Méthodes pour La Détermination
des Orbites des Comètes”, Paris, 1806

10. 10
EstimatorsSOLO
History
Mark Grigorievich Krein
1907 - 1989
Andrey Nikolaevich
Kolmogorov
1903 - 1987
Norbert Wiener
1894 - 1964
The first studies of minimum-mean-square estimation in stochastic
processes were made by Kolmogorov (1939), Krein (1945) and
Wiener (1949)
Kolmogorov, A.N., “Sur l’interpolation et extrapolation des
suites stationaires”, C.R. Acad. Sci. Paris, vol.208, 1939, pp.2043-2045
Krein, M.G., “On a problem of extrapolation of A. N. Kolmogorov”,
C.R. (Dokl) Akad. Nauk SSSR, vol.46, 1945, pp.306-309
Wiener, N., “Extrapolation, Interpolation and Smoothing of
Stationary Time Series, with Engineering Applications”,
MIT Press, Cambridge, MA, 1949 (secret version 1942)
Kolmogorov developed a comprehensive treatment of the linear
prediction problem for discrete-time stochastic processes.
Krein extended the results to continuous time by the lever use of
bilinear transformation.
Wiener, independently, formulated the continuous time linear
prediction problem and derived an explicit formula for the optimal
predictor. Wiener also considered the filtering problem of estimating
a process corrupted by additive noise.

11. 11
Kalman, Rudolf E.
1920 -
Peter Swerling
1929 - 2000
The filter is named after Rudolf E. Kalman, though Thorvald
Nicolai Thiele and Peter Swerling actually developed a similar
algorithm earlier. Stanley F. Schmidt is generally credited with
developing the first implementation of a Kalman filter. It was
during a visit of Kalman to the NASA Ames Research Center that
he saw the applicability of his ideas to the problem of trajectory
estimation for the Apollo program, leading to its incorporation in
the Apollo navigation computer. The filter was developed in
papers by Swerling (1958), Kalman (1960), and Kalman and
Bucy (1961).
Kalman Filter History
Thorvald Nicolai Thiele
1830 - 1910
Stanley F. Schmidt
1926 -
The filter is sometimes called filter due to the fact that it is a special
case of a more general, non-linear filter developed earlier by Ruslan
L. Stratonovich. In fact, equations of the special case, linear filter
appeared in these papers by Stratonovich that were published before
summer 1960, when Rudolf E. Kalman met with Ruslan L.
Stratonovich during a conference in Moscow.
In control theory, the Kalman filter is most commonly referred to as
linear quadratic estimator (LQE).
Kalman, R.E., “A New Approach to Filtering and Prediction Problems”,
J. Basic Eng., March 1960, p. 35-46
Kalman, R.E., Bucy, R.S.,“New Results in Filtering and Prediction Theory”,
J. Basic Eng., March 1961, p. 95-108 Table of Content

12. 12
EstimatorsSOLO
Optimal Parameter Estimate v
H zx
The optimal procedure to estimate depends on the amount of knowledge of the
process that is initially available.
x
The following estimators are known and are used as function of the assumed initial
knowledge available:
Estimators Known initially
Weighted Least Square (WLS)
& Recursive WLS
1
{ } ( ) ( ){ }T
kkkkkkk vvvvERvEv −−== &Markov Estimator2
Maximum Likelihood Estimator3 ( ) ( )xZLxZp xZ ,:|| =
Bayes Estimator4 ( ) ( )Zxporvxp Zxvx |, |,
The amount of assumed initial knowledge available on the process increases in this order.
Table of Content

13. 13
Estimators for Static Systems
z
SOLO
Optimal Weighted Last-Square Estimate
Assume that the set of p measurements, can be expressed as a linear combination,
of the elements of a constant vector plus a random, additive measurement error, :
v
H zx
x v
vxHz +=
( ) ( ) 1
1
−−=−−= −
W
T
xHzxHzWxHzJ

( )T
p
zzzz ,,, 21
=
( )T
n
xxxx ,,, 21
=
( )T
p
vvvv ,,, 21
=
We want to find , the estimation of the constant vector , that minimizes the
cost function:
x

x
that minimizes J, is obtained by solving:0
x

( ) 02/ 1
=−=∂∂=∇ −
xHzWHxJJ T
x

 ( ) zWHHWHx TT 111
0
−−−
=

This solution minimizes J iff :
( ) [ ]( ) ( ) ( ) 02/ 0
1
00
22
0
<−−−=−∂∂− −
xxHWHxxxxxJxx TTT 
or the matrix HT
W-1
H is positive definite.
W is a hermitian (WH
= W, H stands for complex conjugate and matrix transpose),
positive definite weighting matrix.

14. 14
v
H zx
SOLO
Optimal Weighted Least-Square Estimate (continue – 1)
( ) zWHHWHx TT 111
0
−−−
=

Since the mean of the estimate is equal to the estimated parameter, the estimator
is unbiased.
vxHz +=Since is random with mean
{ } { } { } xHvExHvxHEzE =+=+=
0
{ } ( ) { } ( ) xxHWHHWHzEWHHWHxE TTTT
=== −−−−−− 111111
0

is also random with mean:0
x

( ) ( ) ( ) ( )0
1
00
12
00
1
0
*
: xHzWHxxHzWzxHzxHzWxHzJ TTT
W
T 
−+−=−=−−= −−−
Using we want to find the minimum value of J:0
11
xHWHzWH TT −−
=
( ) ( ) ( )0
1
0
0
11
00
1
xHzWzxHWHzWHxxHzWz TTTTT 
  

−=−+−= −−−−
2
0
2
0
1
0
1
0
11
1
0
WW
TTT
HWHx
TT
xHzxHWHxzWzxHWzzWz
TT


−=−=−= −−−−
−
Estimators for Static Systems

15. 15
v
H zx
2
0
22
0
*
111 −−− −=−= WWW
xHzxHzJ

SOLO
Optimal Weighted Least-Square Estimate (continue – 2)
where is a norm.aWaa T
W
12
: −
=
Using we obtain:
0
11
xHWHzWH TT −−
=
( ) ( )
0
,
0
1
0
1
0
0
1
000
0
1
=−=
−=−
−−
−
−
xHWHxzWHx
xHzWxHxHzxH
TT
xHWH
TT
T
W
T





bWaba T
W
1
:, −
=
This suggest the definition of an inner product of two vectors and (relative to the
weighting matrix W) as
ba
Projection Theorem
The Optimal Estimate is such that is the projection (relative to the weighting
matrix W) of on the plane.
0
x

z
0
xH

xH
Table of Content
Estimators for Static Systems

16. 16
v
H zx
2
0
22
0
*
111 −−− −=−= WWW
xHzxHzJ

SOLO
Optimal Weighted Least-Square Estimate (continue – 3)
Projection Theorem
The Optimal Estimate is such that is the projection (relative to the weighting
matrix W) of on the plane.
0
x

z
0
xH

xH
Table of Content
( )
vxHz
zWHHWHx TT
+=
= −−− 111
0

( ) ( ) ( ) vWHHWHxvxHWHHWHxx TTTT 111111
0
−−−−−−
=−+=−

Estimators for Static Systems

17. 18
0z
SOLO
Recursive Weighted Least Square Estimate (RWLS)
Assume that the set of N measurements, can be expressed as a linear combination,
of the elements of a constant vector plus a random, additive measurement error, :
0
v
0
zx 0
H
x v
vxHz += 00
( ) ( ) 1
0
0000
1
0000 −−=−−=
−
W
T
xHzxHzWxHzJ

We found that the optimal estimator ,
that minimizes the cost function:
( )−x

( ) ( ) 0
1
00
1
0
1
00
zWHHWHx
TT −−−
=−
is
Let define the following matrices for the complete measurement set






=





=





=
W
W
W
z
z
z
H
H
H
0
0
:,:,: 0
1
0
1
0
1
( ) ( ) 1
0
1
00
:
−−
=− HWHP
T
Therefore:
( ) ( )
1
1 1
0 0 0 01 1
1 1 1 1 1 1 0 01 1
0 0
0 0
T T T T T T
W H W z
x H W H H W z H H H H
H zW W
−
− −
− −
− −
       
   + = =  ÷     ÷     ÷          

v
H zx
( ) ( ) 0
1
00
zWHPx
T −
−=−

An additional measurement set, is obtained
and we want to find the optimal estimator .
z
( )+x

Estimators for Static Systems

18. 19
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -1)
( ) ( ) 1
0
1
00
:
−−
=− HWHP
T
( ) ( ) 0
1
00
zWHPx
T −
−=−

( ) ( ) [ ] [ ]
( ) ( )zWHzWHHWHHWH
z
z
W
W
HH
H
H
W
W
HHzWHHWHx
TTTT
TTTTTT
1
0
1
00
11
0
1
00
0
1
1
0
0
1
0
1
1
0
01
1
111
1
11
0
0
0
0
−−−−−
−
−
−
−
−
−−
++=




































==+

Define ( ) ( ) HWHPHWHHWHP TTT 111
0
1
00
1
: −−−−−
+−=+=+
( ) ( )[ ] ( ) ( ) ( )[ ] ( )−+−−−−=+−=+
−−−−
PHWHPHHPPHWHPP TT
LemmaMatrixInverse
T 1111
( ) ( )[ ] ( )[ ] ( ) 111111 −−−−−−
+=+−≡+−− WHPWHHWHPWHPHHP TTTTT
( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( )−+−−=−+−−−−=+ −−
PHWHPPPHWHPHHPPP TTT 11
( ) ( )( )
( ) ( ) ( )[ ] ( ){ } ( ) zWHPzWHPHWHPHHPP
zWHzWHPx
TTTT
TT
1
0
1
00
1
1
0
1
00
−−−
−−
++−+−−−−=
++=+

Estimators for Static Systems

19. 20
v
H zx
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -2)
( ) ( )( )
( ) ( ) ( )[ ] ( ){ } ( )
( )
( )
( ) ( )[ ]
( )
( )
( )
( )
( ) ( ) ( ) ( ) zWHPxHWHPx
zWHPzWHPHWHPHHPzWHP
zWHPzWHPHWHPHHPP
zWHzWHPx
TT
T
x
T
WHP
TT
x
T
TTTT
TT
T
11
1
0
1
00
1
0
1
00
1
0
1
00
1
1
0
1
00
1
−−
−
−
−
+
−
−
−
−−−
−−
++−+−−=
++−+−−−−=
++−+−−−−=
++=+
−

      


( ) ( ) 0
1
00
zWHPx
T −
−=−

( ) ( ) HWHPP T 111 −−−
+−=+
( ) ( ) ( ) ( )( )−−++−=+ −
xHzWHPxx T  1
Recursive Weighted Least Square Estimate
(RWLS)
z
( )−x

( )+x

Delay
( ) HWHP T 11 −−
=+
H
( ) 1−
+ WHP T
Estimator
Estimators for Static Systems

20. 21
( ) ( )
( ) ( )[ ]
( ) ( ) ( ) ( )xHzWxHzxHzWxHz
xHz
xHz
W
W
xHzxHz
xHz
xHz
W
W
xHz
xHz
xHzWxHzJ
TT
TT
T
T









−−+−−=






−
−








−−=






−
−












−
−
=−−=
−−
−
−
−
−
1
00
1
000
00
1
1
0
00
00
1
000
11
1
1111
0
0
0
0
( ) 0
1
00
1
: HWHP
T −−
=−
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -3)
Second Way
We want to prove that
where ( ) ( ) 0
1
00
: zWHPx
T −
−=−

( ) ( ) ( )[ ] ( ) ( )[ ]−−−−−=−− −−
xxPxxxHzWxHz
TT  1
00
1
000
Therefore
( )[ ] ( ) ( )[ ] ( ) ( ) ( ) ( ) 11
11
1 −− −+−−=−−+−−−−−= −
−−
WP
TT
xHzxxxHzWxHzxxPxxJ

Estimators for Static Systems

21. 22
( ) 0
1
00
1
: HWHP
T −−
=−
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -4)
Second Way (continue – 1)
We want to prove that
Define
( ) ( ) 0
1
00: zWHPx
T −
−=−

( ) ( )−=−
−
PHWzx
TT
0
1
00

( ) ( )−−= −−
xPzWH
T 1
0
1
00
( ) ( )−−= −− 1
0
1
00 PxHWz TT 
( ) ( ) ( )[ ] ( ) ( )[ ]−−−−−=−− −−
xxPxxxHzWxHz
TT  1
00
1
000
( ) ( )
xHWHxzWHxxHWzzWz
xHzWxHz
TTTTTT
T


0
1
000
1
000
1
000
1
00
00
1
000
−−−−
−
+−−=
−−
( )[ ] ( ) ( )[ ]
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )−−−+−−−−−−−=
−−−−−
−−−−
−
xPxxPxxPxxPx
xxPxx
TTTT
T


1111
1
( ) ( ) xPxxHWz TT 
−−= −− 1
0
1
00
( ) ( )−−= −−
xPxzWx TTT  1
0
1
00
R
( ) xHWHxxPx
TTT 
0
1
00
1 −−
=−
Estimators for Static Systems

22. 23
( ) 0
1
00
1
: HWHP
T −−
=− ( ) ( ) 0
1
00
: zWHPx
T −
−=−

SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -5)
Second Way (continue – 2)
We want to prove that
Define
( ) ( ) ( )[ ] ( ) ( )[ ]−−−−−=−− −−
xxPxxxHzWxHz
TT  1
00
1
00
( ) ( )
xHWHxzWHxxHWzzWz
xHzWxHz
TTTTTT
T


0
1
000
1
000
1
000
1
00
00
1
000
−−−−
−
+−−=
−−
( )[ ] ( ) ( )[ ]
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )−−−+−−−−−−−=
−−−−−
−−−−
−
xPxxPxxPxxPx
xxPxx
TTTT
T


1111
1
( ) ( ) ( ) ( ) 0
1
00
1
0
1
00
1
zWHPHWzxPx
TTT −−−−
−=−−−

Use the identity: ( )
1
00
1
0
1
00
1
0
1
000
1
0
1
0
1
−
−−−−−−






+≡+−
TTT
HIHWWHIHWHHWW
ε
ε
( ) 0lim
1
lim
1
lim
1
00
0
1
00
0
1
00
1
0
0
1
0 ==





=





+−
−
→
−
→
−
−
→
− TTT
HHHHHIHWW ε
εε εεε
( ) ( ) 1
00
1
0
1
0
1
00
1
0
1
000
1
0
1
0
−−−−−−−−
−== WHPHWWHHWHHWW
TTT
( ) ( ) ( ) ( ) 0
1
000
1
00
1
0
1
00
1
zWzzWHPHWzxPx
TTTT −−−−−
=−=−−−

q.e.d.
Estimators for Static Systems

23. 24
( )[ ] ( ) ( )[ ] ( ) ( )xHzWxHzxxPxxJ
TT 
−−+−−−−−= −− 11
1
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -6)
Second Way (continue – 5)
x

Choose that minimizes the scalar cost function
Solution
( ) ( )[ ] ( ) 022 *1*11
=−−−−−=





∂
∂ −−
xHzWHxxP
x
J T
T


Define: ( ) ( ) HWHPP T 111
: −−−
+−=+
Then:
( ) ( )[ ] ( ) ( ) ( ) ( )[ ]−−+−+=+−−+=+ −−−−−−
xHzWHxPzWHxHWHPxP TTT  11111*1
( )[ ] ( ) ( ) zWHxPxHWHP TT 11*11 −−−−
+−−=+−

( ) ( ) ( ) ( )[ ]−−++−=+= −
xHzWHPxxx T  1*
( )[ ] ( )+=+−=





∂
∂ −−− 111
2
1
2
22 PHWHP
x
J T
T

If P-1
(+) is a positive definite matrix then is a minimum solution.*
x

Estimators for Static Systems

24. 25
SOLO
Recursive Weighted Least Square Estimate (RWLS) (continue -7)
( ) ( ) 1
1
−−=−−= −
W
T
xHzxHzWxHzJ

10
1000
000
000
000
2
1
<<


















=
−
−
λ
λ
λ
λ





k
k
W
For W = I (Identity Matrix) we have the Least-Square Estimator (LSE).
How to choose W?
1
If x (i) ≠ constant we can use either one step of measurement or if we assume that
x (i) changes continuously we can choose
2
λ is the fading factor.
Table of Content
Estimators for Static Systems

25. 26
vxHz += 00
v
0H 0zx
( ) zRHHRHx
TT 1
0
1
0
1
00
−−−
=

SOLO
Markov Estimate
For the particular vector measurement equation
where for the measurement noise, we know the mean: { }vEv =
and the variance: ( ) ( ){ }T
vvvvER −−=
v
We choose W = R in WLS, and we obtain:
( ) ( ) 1
0
1
0:
−−
=− HRHP
T
( ) ( ) HRHPP T 111 −−−
+−=+
( ) ( ) ( ) ( )( )−−++−=+ −
xHzRHPxx T  1
RWLS = Markov Estimate
W = R
In Recursive WLS, we obtain for a new
observation: vxHz +=
v
H zx
Table of Content
Estimators for Static Systems

26. 27
vxHz +=
SOLO
Maximum Likelihood Estimate (MLE)
For the particular vector measurement equation
where the measurement noise, is gaussian (normal), with zero mean:
v
H zx
( )RNv ,0~
( )
( )
( )xp
zxp
xzp
x
zx
xz
,
| ,
| =
and independent of , the conditional probability can be written,
using Bayes rule as:
x ( )xzp xz ||
( )










−
−
==−=
1
111
1111
1
1
,
nxpp
nx
pxnxpxnpxpx
xHz
xHz
zxfxHzv
xn
xn

( ) ( )
2/1
,,
/,, T
vxzx
JJvxpzxp =
The measurement noise can be related to and by the function:v zx
pxp
p
pp
p
I
z
f
z
f
z
f
z
f
z
f
J =
















∂
∂
∂
∂
∂
∂
∂
∂
=





∂
∂
=



1
1
1
1
( ) ( ) ( ) ( )vpxpvxpzxp vxvxzx
⋅== ,, ,,
v
Since the measurement noise is independent of :xv
zThe joint probability of and is given by:x
Estimators for Static Systems

27. 28
SOLO
Maximum Likelihood Estimate (continue – 1)
v
H zx
( ) ( ) ( ) ( )vpxpvxpzxp vxvxzx ⋅== ,, ,,
x
v
( )vxp vx
,,
( ) ( )
( )
( ) ( )





−−−=
−=
−
xHzRxHz
R
xHzpxzp
T
p
vxz
1
2/12/
|
2
1
exp
2
1
|
π
( ) ( ) ( )[ ] ( )RWWLSxHzRxHzxzp
T
x
xz
x
⇒−−⇔ −1
| min|max
( ) ( )[ ] ( ) 02 11
=−−=−−
∂
∂ −−
xHzRHxHzRxHz
x
TT
0*11
=− −−
xHRHzRH TT
( ) zRHHRHxx TT 111
*: −−−
==

( ) ( )[ ] HRHxHzRxHz
x
TT 11
2
2
2 −−
=−−
∂
∂ this is a positive definite matrix, therefore
the solution minimizes
and maximizes
( ) ( )[ ]xHzRxHz
T
−− −1
( )xzp xz ||
( ) ( )
( )
( )
( ) 



−=== −
vRv
R
vp
xp
zxp
xzp T
pv
x
zx
xz
1
2/12/
/
|
2
1
exp
2
1,
|
π
Gaussian (normal), with zero mean
( ) ( )xzpxzL xz |:, |=
is called the Likelihood Function and is a measure
of how likely is the parameter given the observation .x z
Estimators for Static Systems

28. 29
SOLO
Maximum Likelihood Estimate (continue – 2)
( ) ( )xzpxzL xz |:, |=
is called the Likelihood Function and is a measure
of how likely is the parameter given the observation .x z
Estimators for Static Systems
Fisher, Sir Ronald Aylmer
1890 - 1962
R.A. Fisher first used the term Likelihood. His reason for the
term likelihood function was that if the observation is and
, then it is more likely that the true value of
is than .
zZ =
( ) ( )21 ,, xzLxzL >
1x 2xX

29. 30
SOLO
Bayesian Maximum Likelihood Estimate (Maximum Aposterior – MAP Estimate)
v
H zx
vxHz +=
Consider a gaussian vector , where ,
measurement, , where the Gaussian noise
is independent of and .( )Rv ,0~ N
v
x ( ) ( )[ ]−− Pxx ,~

N
x
( )
( ) ( )
( )( ) ( ) ( )( )





−−−−−−
−
= −
xxPxx
P
xp
T
nx
 1
2/12/
2
1
exp
2
1
π
( ) ( )
( )
( ) ( )





−−−=−= −
xHzRxHz
R
xHzpxzp
T
pvxz
1
2/12/|
2
1
exp
2
1
|
π
( ) ( ) ( ) ( )∫∫
+∞
∞−
+∞
∞−
== xdxpxzpxdzxpzp xxzzxz |, |,
is Gaussian with( )zpz ( ) ( ) ( ) ( ) ( )−=+=+= xHvExEHvxHEzE

0
( ) ( )[ ] ( )[ ]{ } ( )[ ] ( )[ ]{ }
( )( )[ ] ( )( )[ ]{ } ( )[ ] ( )[ ]{ }
( )[ ]{ } ( )[ ]{ } { } ( ) RHPHvvEHxxvEvxxEH
HxxxxEHvxxHvxxHE
xHvxHxHvxHEzEzzEzEz
TTTTT
TTT
TT
+−=+−−−−−−
−−−−=+−−+−−=
−−+−−+=−−=
  

  



00
cov
( )
( ) ( )
( )[ ] ( )[ ] ( )[ ]






−−+−−−−
+−
=
−
xHzRHPHxHz
RHPH
zp TT
Tpz
ˆˆ
2
1
exp
2
1 1
2/12/
π
Estimators for Static Systems

30. 31
SOLO
Bayesian Maximum Likelihood Estimate (Maximum Aposterior Estimate) (continue – 1)
v
H zx
vxHz +=
Consider a Gaussian vector , where ,
measurement, , where the Gaussian noise
is independent of and .( )Rvv ,0;~ N
v
x ( ) ( )[ ]−− Pxxx ,;~

N
x
( )
( ) ( )
( )( ) ( ) ( )( )





−−−−−−
−
= −
xxPxx
P
xp
T
nx
 1
2/12/
2
1
exp
2
1
π
( ) ( )
( )
( ) ( )



−−−=−= −
xHzRxHz
R
xHzpxzp
T
pvxz
1
2/12/|
2
1
exp
2
1
|
π
( )
( ) ( )
( )[ ] ( )[ ] ( )[ ]






−−+−−−−
+−
=
−
xHzRHPHxHz
RHPH
zp TT
Tpz
ˆˆ
2
1
exp
2
1 1
2/12/
π
( )
( ) ( )
( )
( )
( )
( )
( ) ( ) ( )( ) ( ) ( )( ) ( )[ ] ( )[ ] ( )[ ]





−−+−−−+−−−−−−−−−⋅
+−
−
==
−−−
xHzRHPHxHzxxPxxxHzRxHz
RHPH
RPzp
xpxzp
zxp
TTTT
T
nz
xxz
zx
ˆˆ
2
1
2
1
2
1
exp
2
1|
|
111
2/1
2/12/1
2/
|
|

π
from which
Estimators for Static Systems

31. 32
SOLO
Bayesian Maximum Likelihood Estimate (Maximum Aposterior Estimate) (continue – 2)
( ) ( ) ( )( ) ( ) ( )( ) ( )( ) ( )[ ] ( )( )−−+−−−−−−−−−+−−
−−−
xHzRHPHxHzxxPxxxHzRxHz TTTT  111
( ) ( )( )[ ] ( ) ( )( )[ ] ( )( ) ( ) ( )( )
( )( ) ( )[ ] ( )( ) ( )( ) ( )[ ]{ } ( )( )
( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )[ ] ( )( )−−+−−−+−−−−−−−−−−
−−+−−−−=−−+−−−−
−−−−−+−−−−−−−−−−=
−−−−
−−−
−−
xxHRHPxxxxHRxHzxHzRHxx
xHzRHPHRxHzxHzRHPHxHz
xxPxxxxHxHzRxxHxHz
TTTTT
TTTT
TT



1111
111
11
( )( ) ( )( ) ( )( ) ( ) ( )( ) ( )( ) ( )[ ] ( )( )−−+−−−−−−−−−+−−−−
−−−
xHzRHPHxHzxxPxxxHzRxHz TTTT  111
( )[ ] ( )[ ] 11111111 −−−−−−−−
−++/−/=+−− RHPHRHHRRRRHPHR TTT
we have
then
Define: ( ) ( )[ ] 111
:
−−−
+−=+ HRHPP T
( )( ) ( ) ( )[ ] ( ) ( )( )
( )( ) ( ) ( )[ ] ( )( ) ( )( ) ( ) ( )[ ] ( )( )
( )( ) ( )[ ] ( )( )−−+−−−+
−−++−−−−−++−−−
−−+++−−=
−−
−−−−
−−−
xxHRHPxx
xxPPHRxHzxHzRHPPxx
xHzRHPPPHRxHz
TT
TTT
TT



11
1111
111
( ) ( ) ( )( )[ ] ( ) ( ) ( ) ( )( )[ ]−−++−−+−−++−−= −−−
xHzRHPxxPxHzRHPxx TTT  111
( )
( ) ( )
( ) ( ) ( )( )[ ] ( ) ( ) ( ) ( )( )[ ]






−−+−−−+−−+−−−−⋅
+
= −−−
xHzRHPxxPxHzRHPxx
P
zxp TTT
nzx
 111
2/12/|
2
1
exp
2
1
|
π
Estimators for Static Systems

32. 33
SOLO
Bayesian Maximum Likelihood Estimate (Maximum Aposterior Estimate) (continue – 3)
then
where: ( ) ( )[ ] 111
:
−−−
+−=+ HRHPP T
( )
( ) ( )
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ]






−+−−−+−+−−−−⋅
+
= −−−
xHzRHPxxPxHzRHPxx
P
zxp TTT
nzx
111
2/12/|
2
1
exp
2
1
|

π
( )zxp zx
x
|max | ( ) ( ) ( ) ( )( )−−++−==+ −
xHzRHPxxx T  1*
:
Table of Content
Estimators for Static Systems

33. 34
Estimators
v
( )vxh ,
z
x
Estimator
x

SOLO
The Cramér-Rao Lower Bound (CRLB) on the Variance of the Estimator
{ }xE

- estimated mean vector
[ ]( ) [ ]( ){ } { } { } { }TTT
x xExExxExExxExE

 −=−−=
2
σ - estimated variance matrix
For a good estimator we want
{ } xxE =

- unbiased estimator vector
{ } { } { }TT
x xExExxE

 −=
2
σ - minimum estimation variance
( ) ( ){ }Tk
kzzZ 1:= - the observation matrix after k observations
( ) ( ) ( ){ }xkzzLxZL k
,,,1, = - the Likelihood or the joint density function of Zk
We have:
( )T
pzzzz ,,, 21 = ( )T
n
xxxx ,,, 21
= ( )T
pvvvv ,,, 21 =
The estimation of , using the measurements
of a system corrupted by noise is a random variable with
xˆ x z
v
( ) ( ) ( ) ( )∫== dvvpxvZpxZpxZL v
k
vz
k
xz
k
;||, ||
( ) ( )[ ]{ } ( ) ( )[ ] ( ) ( )[ ] ( ) ( )
[ ] [ ] ( )xbxZdxZLZx
kzdzdxkzzLkzzxkzzxE
kkk
+==
=
∫
∫
,
1,,,1,,1,,1





- estimator bias( )xb
therefore:

34. 35
Estimators
v
( )vxh ,
z
x
Estimator
x

SOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 1)
[ ]{ } [ ] [ ] ( )xbxZdxZLZxZxE kkkk
+== ∫ ,

We have:
[ ]{ } [ ] [ ] ( )
x
xb
Zd
x
xZL
Zx
x
ZxE k
k
k
k
∂
∂
+=
∂
∂
=
∂
∂
∫ 1
,

Since L [Zk
,x] is a joint density function, we have:
[ ] 1, =∫
kk
ZdxZL
[ ] [ ] [ ] [ ]0
,,
0
,
=
∂
∂
=
∂
∂
→=
∂
∂
∫∫∫
k
k
k
k
k
k
Zd
x
xZL
xZd
x
xZL
xZd
x
xZL
[ ]( ) [ ] ( )
x
xb
Zd
x
xZL
xZx k
k
k
∂
∂
+=
∂
∂
−∫ 1
,
Using the fact that: [ ] [ ] [ ]
x
xZL
xZL
x
xZL k
k
k
∂
∂
=
∂
∂ ,ln
,
,
[ ]( ) [ ] [ ] ( )
x
xb
Zd
x
xZL
xZLxZx k
k
kk
∂
∂
+=
∂
∂
−∫ 1
,ln
,


35. 36
EstimatorsSOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 2)
[ ]( ) [ ] [ ] ( )
x
xb
Zd
x
xZL
xZLxZx k
k
kk
∂
∂
+=
∂
∂
−∫ 1
,ln
,

Hermann Amandus
Schwarz
1843 - 1921
Let use Schwarz Inequality:
( ) ( ) ( ) ( )∫∫∫ ≤ dttgdttfdttgtf
22
2
The equality occurs if and only if f (t) = k g (t)
[ ]( ) [ ] [ ] [ ]xZL
x
xZL
gxZLxZxf k
k
kk
,
,ln
:&,:
∂
∂
=−=
choose:
[ ]( ) [ ] [ ]
( ) [ ]( ) [ ]( ) [ ] [ ]














∂
∂
−≤





∂
∂
+=






∂
∂
−
∫∫
∫
k
k
kkkk
k
k
kk
Zd
x
xZL
xZLZdxZLxZx
x
xb
Zd
x
xZL
xZLxZx
2
2
2
2
,ln
,,1
,ln
,


[ ]( ) [ ]
( )
[ ] [ ]
∫
∫






∂
∂






∂
∂
+
≥−
k
k
k
kkk
Zd
x
xZL
xZL
x
xb
ZdxZLxZx 2
2
2
,ln
,
1
,


36. 37
EstimatorsSOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 3)
[ ]( ) [ ]
( )
[ ] [ ]
∫
∫






∂
∂






∂
∂
+
≥−
k
k
k
kkk
Zd
x
xZL
xZL
x
xb
ZdxZLxZx 2
2
2
,ln
,
1
,

This is the Cramér-Rao bound for a biased estimator
Harald Cramér
1893–1985
Cayampudi Radhakrishna
Rao
1920 -
[ ]{ } ( ) [ ] 1,& =+= ∫
kkk
ZdxZLxbxZxE

[ ]( ) [ ] [ ] [ ]{ } ( )( ) [ ]
[ ] [ ]{ }( ) [ ] ( ) [ ] [ ]{ }( ) [ ]
( ) [ ]
  
  


1
2
0
2
22
,
,2,
,,
∫
∫∫
∫∫
+
−+−=
+−=−
kk
kkkkkkkk
kkkkkkk
ZdxZLxb
ZdxZLZxEZxxbZdxZLZxEZx
ZdxZLxbZxEZxZdxZLxZx
[ ] [ ]{ }( ) [ ]
( )
[ ] [ ]
( )xb
Zd
x
xZL
xZL
x
xb
ZdxZLZxEZx
k
k
k
kkkk
x
2
2
2
22
,ln
,
1
, −






∂
∂






∂
∂
+
≥−=
∫
∫

σ

37. 38
EstimatorsSOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 4)
[ ] [ ]{ }( ) [ ]
( )
[ ] [ ]
( )xb
Zd
x
xZL
xZL
x
xb
ZdxZLZxEZx
k
k
k
kkkk
x
2
2
2
22
,ln
,
1
, −






∂
∂






∂
∂
+
≥−=
∫
∫

σ
[ ] [ ]
[ ]
[ ]
[ ] [ ] [ ] 0,
,ln
0
,
1,
,
,
,ln
=
∂
∂
→=
∂
∂
→= ∫∫∫
∂
∂
=
∂
∂
kk
kxZL
x
xZL
x
xZL
k
k
kk
ZdxZL
x
xZL
Zd
x
xZL
ZdxZL
k
k
k
[ ] [ ] [ ] [ ] [ ]
[ ]
0,
,ln,ln
,
,ln
,
2
2
=
∂
∂
∂
∂
+
∂
∂
→ ∫∫
∂
∂
∂
∂
k
x
xZL
k
kk
kk
kx
ZdxZL
x
xZL
x
xZL
ZdxZL
x
xZL
k
  
[ ] [ ] 0
,ln,ln
2
2
2
=














∂
∂
+






∂
∂
→
∂
∂
x
xZL
E
x
xZL
E
kkx
( )
[ ]
( )
( )
[ ]
( )xb
x
xZL
E
x
xb
xb
x
xZL
E
x
xb
k
k
x
2
2
2
2
2
2
2
2
,ln
1
,ln
1
−






∂
∂






∂
∂
+
−=−














∂
∂






∂
∂
+
≥σ

38. 39
Estimators
[ ]( ) [ ]
( )
[ ]
( )
[ ]






∂
∂






∂
∂
+
−=














∂
∂






∂
∂
+
≥−∫
2
2
2
2
2
2
,ln
1
,ln
1
,
x
xZL
E
x
xb
x
xZL
E
x
xb
ZdxZLxZx kk
kkk
SOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 5)
( )
[ ]
( )
( )
[ ]
( )xb
x
xZL
E
x
xb
xb
x
xZL
E
x
xb
k
k
x
2
2
2
2
2
2
2
2
,ln
1
,ln
1
−






∂
∂






∂
∂
+
−=−














∂
∂






∂
∂
+
≥σ
For an unbiased estimator (b (x) = 0), we have:
[ ] [ ]






∂
∂
−=














∂
∂
≥
2
22
2
,ln
1
,ln
1
x
xZL
E
x
xZL
E
k
k
x
σ
http://www.york.ac.uk/depts/maths/histstat/people/cramer.gif

39. 40
Estimators
[ ]( ) [ ]( ) [ ] [ ]( ) [ ]( ){ }
( ) [ ] [ ] ( )
( ) [ ] ( )






∂
∂
+
















∂
∂






∂
∂
+−=






∂
∂
+






















∂
∂






∂
∂






∂
∂
+≥
−−=−−
−
−
∫
x
xb
I
x
xZL
E
x
xb
I
x
xb
I
x
xZL
x
xZL
E
x
xb
I
xZxxZxEZdxZLxZxxZx
x
k
T
x
T
kk
T
x
TkkkkTkk
1
2
2
1
,ln
,ln,ln
,

SOLO
The Cramér-Rao Lower Bound on the Variance of the Estimator (continue – 5)
The multivariable form of the Cramér-Rao Lower Bound is:
[ ]( )
[ ]
[ ] 









−
−
=−
n
k
n
k
k
xZx
xZx
xZx




11
[ ]( ) [ ]
[ ]
[ ]
















∂
∂
∂
∂
=





∂
∂
=∇
n
k
k
k
k
x
x
xZL
x
xZL
x
xZL
xZL
,ln
,ln
,ln
,ln
1

Fisher Information Matrix
[ ] [ ] [ ]








∂
∂
−=














∂
∂






∂
∂
=
x
k
x
T
kk
x
xZL
E
x
xZL
x
xZL
E 2
2
,ln,ln,ln
:J
Fisher, Sir Ronald Aylmer
1890 - 1962

40. 41
Fisher, Sir Ronald Aylmer (1890-1962)
The Fisher information is the amount of information that
an observable random variable z carries about an unknown
parameter x upon which the likelihood of z, L(x) = f(Z; x),
depends. The likelihood function is the joint probability of
the data, the Zs, conditional on the value of x, as a function
of x. Since the expectation of the score is zero, the variance
is simply the second moment of the score, the derivative of
the lan of the likelihood function with respect to x. Hence
the Fisher information can be written
( ) [ ]( ) [ ]( ){ } [ ]( ){ }x
k
xx
x
Tk
x
k
x
xZLExZLxZLEx ,ln,ln,ln: ∇∇−=∇∇=J
Table of Content

41. 42
Estimators
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
kkkk
kkkkkkk
vxHz
wuGxx
+=
Γ++Φ= −−−−−− 111111
SOLO
Kalman Filter Discrete Case
Assume a discrete dynamic system
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

kkkkkkk zKxKx += −1||
ˆ'ˆ
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
vvv kRlekeEkvEkvke ,
0
&: δ=−=
 ( ) ( ){ } ( ) 1, −= lk
T
vw kMlekeE δ
Let find a Linear Filter that works in two stages:
s.t. will minimize (by choosing the optimal gains Kk and Kk’ )
( ) ( ){ } { }
kkkkk
kk
T
kkkkk
T
kkkk
xxxwhere
xxExxxxEJ
−=
=−−=
||
||||
ˆ:~
~~ˆˆ
{ } { }kkk xExE =|
ˆ Unbiased Estimator { } { } { } { }0ˆ~
|| =−= kkkkk xExExE



=
≠
=
lk
lk
lk
1
0
,δ
111|111|
ˆˆ −−−−−− +Φ= kkkkkkk uGxx
kz1. One step prediction, before the measurement ,based on the estimation at step k-1 :1|
ˆ −kkx
2. Update after the measurement is received:kz

42. 43
Estimators
kkkkk xxx −= −− 1|1|
ˆ:~
kkkkkkk zKxKx += −1||
ˆ'ˆ
SOLO
Kalman Filter Discrete Case (continue – 1)
Define
kkkkk xxx −= ||
ˆ:~
The Linear Estimator we want is:
Therefore
[ ] [ ] [ ] kkkkkkkkk
z
kkkk
x
kkkkkkk vKxKxIHKKvxHKxxKxx
kkk
++−+=++++−= −−
−
1|
ˆ
1||
~''~'~
1|

Unbiaseness conditions: { } { } 0~~
1|| == −kkkk xExE
gives: { } [ ] { } { } { } 0~''~
00
1|
0
| =++−+= −
 kkkkkkkkkkk vEKxEKxEIHKKxE
or: kkk HKIK −='
Therefore the Unbiased Linear Estimator is:
[ ]1|1||
ˆˆˆ −− −+= kkkkkkkkk xHzKxx

43. 44
Estimators



+=
Γ++Φ= −−−−−−
kkkk
kkkkkkk
vxHz
wuGxx 111111
SOLO
Kalman Filter Discrete Case (continue – 2)
The discrete dynamic system
The Linear Filter
(Linear Observer)[ ]



−++=
+Φ=
−−−−
−−−−−−
1|111||
111|111|
ˆˆˆ
ˆˆ
kkkkkkkkkkk
kkkkkkk
xHzKuGxx
uGxx
111|111|1|
~ˆ:~
−−−−−−− Γ−Φ=−= kkkkkkkkkk wxxxx
{ } T
kkk
T
kkkk
T
kkkkkk QPxxEP 11111|111|1|1|
~~: −−−−−−−−−− ΓΓ+ΦΦ==
{ } { } { }
{ } { } { } { }
{ } { } { }0~
00
0~~
1111
1
1||
==
==
==
−−−−
−
−
T
kk
T
kk
kk
kkkk
wxEwxE
wEvE
xExE
{ }
[ ] [ ]{ }
{ } { }
{ } { } T
k
T
kkk
T
k
T
kkk
T
k
T
kkk
T
k
T
kkk
T
k
T
k
T
k
T
kkkkk
T
kkkkkk
wwExwE
wxExxE
wxwxE
xxEP
11111
0
111
1
0
1111111
11111111
1|1|1|
~
~~~
~~
~~:
−−−−−−−−
−−−−−−−−
−−−−−−−−
−−−
ΓΓ+ΦΓ−
ΓΦ−ΦΦ=
Γ−ΦΓ−Φ=
=


{ } { } { } 1111
0
1|111|
1
~~
−−−−−−−− Γ−=Γ−Φ=
−
kk
M
T
kkkkkkk
T
kkk MvwEvxEvxE
k


44. 45
EstimatorsSOLO
Kalman Filter Discrete Case (continue – 3)
{ }kkkkkkkkkkkk vxHKxxxx −−=−= −− 1|1|||
~~ˆ:~
{ } ( )[ ] ( )[ ]{ }T
k
T
k
T
k
T
kk
T
kkkkkkkkk
T
kkkkkk KvHxxvxHKxExxEP −−−−== −−−− 1|1|1|1||||
~~~~~~:
{ } 111|
~
−−− Γ−= kk
T
kkk MvxE
( ) { }( ) { }[ ]
{ }( ) { }[ ]T
k
T
kkk
T
k
T
k
T
kkkk
T
k
T
kkk
T
k
T
k
T
kkkkkk
KxvEKHIxvEK
KvxEKHIxxEHKI
1|1|
1|1|1|
~~
~~~
−−
−−−
+−+
+−−=
( ) { } ( ) { }
( ) ( )T
kk
T
k
T
kk
T
kkkkk
T
k
R
T
kkk
T
kk
P
T
kkkkkk
HKIMKKMHKI
KvvEKHKIxxEHKI
kkk
−Γ−Γ−−
+−−=
−−−−
−−
−
1111
1|1|
1|
~~
  



+=
Γ++Φ= −−−−−−
kkkk
kkkkkkk
vxHz
wuGxx 111111
The discrete dynamic system
The Linear Filter
(Linear Observer)[ ]



−++=
+Φ=
−−−−
−−−−−−
1|111||
111|111|
ˆˆˆ
ˆˆ
kkkkkkkkkkk
kkkkkkk
xHzKuGxx
uGxx

45. 46
EstimatorsSOLO
Kalman Filter Discrete Case (continue – 4)
{ }
( ) ( ) ( ) ( )T
kk
T
k
T
kk
T
kkkkk
T
kkk
T
kkkkkk
T
kkkkkk
HKIMKKMHKIKRKHKIPHKI
xxEP
−Γ−Γ−−+−−=
=
−−−−− 11111|
|||
~~:
{ } ( ) ( )
( ) T
k
T
kkkk
T
k
T
k
T
kkkkkk
T
k
T
kkkkk
T
kkk
T
kkkkk
T
kkkkkk
KHPHHMMHRK
MPHKKMHPPxxEP
1|1111
111|111|1||||
~~:
−−−−−
−−−−−−−
+Γ+Γ++
Γ+−Γ+−==
Completion of Squares
[ ]

[ ]
[ ] [ ] 

















+Γ+Γ+Γ+−
Γ+−
=
−−−−−−−−
−−−−
T
k
C
T
kkkk
T
k
T
k
T
kkkkk
B
T
k
T
kkkk
B
kk
T
kkk
A
kk
kkk
K
I
HPHHMMHRMPH
MHPP
KIP
T
    
  
1|1111111|
111|1|
|
Joseph Form (true for all Kk)

46. 47
Estimators
{ } { } kk
K
T
kk
K
k
T
k
K
k
K
PtracexxEtracexxEJ
kkkk
|min~~min~~minmin ===
SOLO
Kalman Filter Discrete Case (continue – 5)
Completion of Squares
Use the Matrix Identity: 





−






 −





 −
=





−
−
−
∆
−
−
IBC
I
C
BCBA
I
CBI
CB
BA
T
T
T 1
1
1
0
0
0
0

{ } [ ] [ ] ( ) 







−







+Γ+Γ+
∆
−== −
−−−−−
−
T
k
T
kkkk
T
k
T
k
T
kkkkk
k
k
T
kkkkkk
CBK
I
HPHHMMHR
CBKIxxEP 1
1|1111
1
|||
0
0
~~:
to obtain
( ) ( ) ( )T
k
T
kkkk
T
kkkk
T
k
T
k
T
kkkkkkk
T
kkkkkk MPHHPHHMMHRMHPP 111|
1
1|1111111|1|: −−−
−
−−−−−−−−− Γ++Γ+Γ+Γ+−=∆
[ ]

[ ]
[ ] [ ] 

















+Γ+Γ+Γ+−
Γ+−
=
−−−−−−−−
−−−−
T
k
C
T
kkkk
T
k
T
k
T
kkkkk
B
T
k
T
kkkk
B
kk
T
kkk
A
kk
kkk
K
I
HPHHMMHRMPH
MHPP
KIP
T
    
  
1|1111111|
111|1|
|

47. 48
Estimators
{ } { } kk
T
kkkkkk
T
kkk PtracexxEtracexxEJ |||||
~~~~ ===
[ ][ ]    
1
1
1|1111111|
..*
−
−
−−−−−−−− +Γ+Γ+Γ+==
C
T
kkkk
T
k
T
k
T
kkkkk
B
kk
T
kkk
FK
kk HPHHMMHRMHPKK
SOLO
Kalman Filter Discrete Case (continue – 6)
To obtain the optimal K (k) that minimizes J (k+1) we perform
[ ] [ ]{ } 011|
=−−+∆
∂
∂
=
∂
∂
=
∂
∂ −− T
kkk
kk
kk
k
k
CBKCCBKtrace
KK
Ptrace
K
J
Using the Matrix Equation: (see next slide){ } ( )TT
BBAABAtrace
A
+=
∂
∂
[ ]( ) 01*|
=+−=
∂
∂
=
∂
∂ − T
k
k
kk
k
k
CCCBK
K
Ptrace
K
J
we obtain
or
Kalman Filter Gain
( ) ( )( ) ( )
( ){ }T
kk
T
kkkkkk
B
T
kk
T
kkk
C
T
kkkk
T
k
T
k
T
kkkkk
B
kk
T
kkk
A
kkkkk
K
MHPKPtrace
MHPHPHHMMHRMHPPtracetracePtracekJ
T
111|1|
111|
1
1|1111111|1||min
1
min
−−−−
−−−
−
−−−−−−−−−
Γ+−=








Γ++Γ+Γ+Γ+−=∆==
−
      
( ) [ ]T
kkkk
T
k
T
k
T
kkkkk
T
k
kk
k
k
HPHHMMHRCC
K
Ptrace
K
J
1|11112
|
2
2
2
2 −−−−− +Γ+Γ+=+=
∂
∂
=
∂
∂

48. 49
MatricesSOLO
Differentiation of the Trace of a square matrix
[ ] ( )
( )
∑∑∑∑∑∑
=
==
l p k
lkpklp
aa
l p k
T
klpklp
T
abaabaABAtrace
lk
T
kl
[ ]T
ABAtrace
A∂
∂
[ ] ∑∑ +=
∂
∂
p
pjip
k
ikjk
T
ij
baabABAtrace
a
[ ] ( )TTT
BBABABAABAtrace
A
+=+=
∂
∂

49. 50
Estimators
( ) 1
1|1|*
−
−− +=
T
kkkkk
T
kkkk HPHRHPK
( ) ( ) T
kkk
T
kkkkkkkk KRKHKIPHKIP ***** 1|| +−−= −
SOLO
Kalman Filter Discrete Case (continue – 7)
we found that the optimal Kk that minimizes Jk is
( ) 1|
1
1|1|1| −
−
−−− +−= kkk
T
kkkkk
T
kkkkk PHHPHRHPP
( ) [ ] 1|
111
1|
&
*11 −
−−−
− −=+=−− kkkkkk
T
kkk
LemmaMatrixInverse
existRP
PHKIHRHP
kk
When Mk = 0, where:
( ) ( ){ } 1, −= lkk
T
vw MlekeE δ

50. 51
Estimators
SOLO
Kalman Filter Discrete Case (continue – 8)
We found that the optimal Kk that minimizes Jk (when Mk-1 = 0 ) is
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] 1
1|1111|11*
−
+++++++=+ kHkkPkHkRkHkkPkK TT
( ) ( ) 1111
1|
11
&
1
1| 1
1|
1
−−−−
−
−−−
− +−=+ −
−
− k
T
kkk
T
kkkkkk
LemmaMatrixInverse
existPR
T
kkkkk RHHRHPHRRHPHR
kkk
( ) 1111
1|
1
1|
1
1|*
−−−−
−
−
−
−
− +−= k
T
kkk
T
kkkkk
T
kkkk
T
kkkk RHHRHPHRHPRHPK
( ){ } ( ) 1111
1|
111
1|1|
−−−−
−
−−−
−− +−+= k
T
kkk
T
kkkkk
T
kkk
T
kkkkk RHHRHPHRHHRHPP
[ ] 1
1|
1111
1|*
−
−
−−−−
− =+= k
T
kkkk
T
kkk
T
kkkk RHPRHHRHPK
If Rk
-1
and Pk|k-1
-1
exist:
Table of Content

51. 52
Estimators
SOLO
Kalman Filter Discrete Case (continue – 9)
Properties of the Kalman Filter
{ } 0~ˆ || =
T
kkkk xxE
Proof (by induction):
( )
1111
00000001 0
vxHz
xxwuGxx
+=
=Γ++Φ=k=1:
( ) { }
( )
( )0010|00110010010011000|00
0010|0011111000|00
00|00|1111000|001|1
ˆˆ
ˆˆ
ˆˆˆˆ
uGHxHvwHuGHxHKuGx
uGHxHvxHKuGx
xExxHzKuGxx
−Φ−+Γ++Φ++Φ=
−Φ−+++Φ=
=−++Φ=
( ) 1100110|00110|0011|11|1
~~ˆ~ vKwIHKxHKxxxx +Γ−+Φ−Φ=−=
{ } ( )[ ]{ 100110|001000|001|11|1
~ˆ~ˆ vwHKxKuGxExxE
T
+Γ+Φ−+Φ=
( )[ ] }T
vKwIHKxHKx 1100110|00110|00
~~ +Γ−+Φ−Φ
{ }( ) { } ( )
{ } T
R
T
TTT
Q
TTT
P
T
KvvEK
IKHwwEHKHKIxxEHK
1111
110000110110|00|0011
1
00|0
~~


+
−ΓΓ+Φ−Φ−=
1

52. 53
Estimators
SOLO
Kalman Filter Discrete Case (continue – 10)
Properties of the Discrete Kalman Filter
{ } 0~ˆ || =
T
kkkk xxE
Proof (by induction) (continue – 1):
k=1 :
{ } ( ) ( ) TTTTTTT
KRKIKHQHKHKIPHKxxE 11111000110110|00111|11|1
~ˆ +−ΓΓ+Φ−Φ−=
1
( ) ( ) TTT
P
TT
P
TT
KRKKHQPHKQPHK 1111100000|001100000|0011
0|10|1
+ΓΓ+ΦΦ+ΓΓ+ΦΦ−=
    
[ ] [ ] 0
1
111|11
1|1
111|111111110|111
−
=
=+−=+−−=
RHPK
TTT
P
TT
T
T
KRPHKKRKKHIPHK
  
In the same way we continue for k > 1 and by induction we prove the result.
Table of Content

53. 54
Estimators
SOLO
Kalman Filter Discrete Case (continue – 9)
Properties of the Kalman Filter
{ } 1,,10~
| −== kjzxE
T
jkk 
Proof:
( )
jjjj
kkkkkkkkk
vxHz
xHzKxx
+=
−+= −− 1|1||
ˆˆˆ
2
( ) ( ) kkkkkkkkkkkkkkkkkkkkk vKxHKIxxHvxHKxxxx +−=−−++=−= −−− 1|1|1|||
~ˆˆˆ:~
{ } ( )[ ]( ){ }
( ) { } ( ) { } { } { }
jkkR
T
jkk
T
j
jk
T
jkk
jk
T
jkkkk
T
j
T
jkkkk
T
jjjkkkkkkjkk
vvEKHxvEKvxEHKIHxxEHKI
vxHvKxHKIEzxE
,00
1|1|
1||
~~
~~
δ
++−+−=
++−=
→>→>
−−
−
{ } ( )[ ]{ } ( ) { } { }
0
1|1||
~~~
→>
−− +−=+−=
jk
T
jkk
T
jkkkk
T
jkkkkkk
T
jkk zvEKzxEHKIzvKxHKIEzxE

54. 55
Estimators
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
kkkk
kkkkkkk
vxHz
wuGxx
+=
Γ++Φ= −−−−−− 111111
SOLO
Kalman Filter Discrete Case - Innovation
Assume a discrete dynamic system
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
vvv kRlekeEkvEkvke ,
0
&: δ=−=

( ) ( ){ } lklekeE
T
vw ,0 ∀=



=
≠
=
lk
lk
lk
1
0
,δ
kkkkkkkk vxHzz +−=−= −− 1|1|
~ˆ:ι
Innovation is defined as:
The Linear Filter
(Linear Observer)


















−+=
+Φ=
−
−−
−−−−−−
  

k
kkz
kkkkkkkkk
kkkkkkk
xHzKxx
uGxx
ι
1|ˆ
1|1||
111|111|
ˆˆˆ
ˆˆ
111|1111|1|
~ˆ:~
−−−−−−−− Γ−Φ=−= kkkkkkkkkk wxxxx
{ } { } { } { }0~
00
1| =+−= −
 kkkkk vExEHE ι
( ) 1
1|1|
..
:
−
−− += k
T
kkkkkkk
FK
k RHPHPHK
2
Properties of the Discrete Kalman Filter

55. 56
Estimators
( )
[ ]
( )∑+=
+−++−
−−−−−−−−
−+
Γ−Φ+=
=
Γ−Φ+Γ−Φ+=
Γ−Φ+−Φ=Γ−Φ=
++
i
jk
kkkkk
F
kiijj
F
jii
iiiiiiiiiiiiii
iiiiiii
F
iiiiiiiiii
wvKFFFxFFF
wvKwvKxFF
wvKxHKIwxx
kiji
i
1
11|111
111112|11
1|||1
1,1,
~
~
~~~





  
SOLO
Kalman Filter Discrete Case – Innovation (continue – 1)
Assume i > j:
{ } { } { }
{ }
{ }
{ }
∑+=
→+≥
+
→+≥
++
+
+++++








Γ−Φ+=
i
jk
jk
T
jjkk
jk
T
jjkkkki
jPj
T
jjjjji
T
jjji xwExvEKFxxEFxxE
1
01
|1
01
|11,
|1
|1|11,|1|1
~~~~~~
  
( )
iiikiiki
iiii
FFFFFF
HKIF
==
−Φ=
− :&:
:
,1, 
( ) ( ) iiiiiiiiiiiiiii vKxHKIvxHKxx +−=−−= −−− 1|1|1||
~~~~
{ } ( )( ){ }T
j
T
j
T
jjiiii
T
ji vHxvxHEE +−+−= −− 1|1|
~~ιι
{ } { } { } { }T
ji
T
j
T
jji
T
jiii
T
j
T
jjiii vvEHxvEvxEHHxxEH +−−= −−−− 1|1|1|1|
~~~~
jjjjjjj wxx Γ−Φ=+ ||1
~~
{ } jjji
T
jjji PFxxE |11,|1|1
~~
++++ =

56. 57
Estimators
( )∑+=
++++ Γ−Φ+=
i
jk
kkkkkkijjjiji wvKFxFx
1
1,|11,|1
~~
SOLO
Kalman Filter Discrete Case – Innovation (continue – 2)
Assume i > j:
{ } { } { }
( )
0~~
0
1
0
|1|1|1
,
=Γ−Φ=
→>⇒
+
→>
+
>
++
T
j
jijM
T
ji
T
j
ji
T
jji
ji
T
jjji
ji
T
wvExvExvE

δ
( )
iiikiiki
iiii
FFFFFF
HKIF
==
−Φ=
− :&:
:
,1, 
{ } { }
{ }
{ } { }
{ }
1112,
1
0
111,
0
1|11,|1|1
1,1
~~
++++
+=
++++++++
Φ=










Γ−Φ+= ∑
++
jjjji
i
jk
T
jkk
R
T
jkkkki
T
jjjji
T
jjji
RKF
vwEvvEKFvxEFvxE
jkj
  
δ
{ } 1,1111 +++++ = jij
T
ji RvvE δ
{ } { } { } { } { }T
ji
T
j
T
jji
T
jiii
T
j
T
jjiii
T
ji vvEHxvEvxEHHxxEHE 111|111|111|1|1111
~~~~
++++++++++++++ +−−=ιι
jjjjjjj wxx Γ−Φ=+ ||1
~~

57. 58
Estimators
[ ] 1
11|111|11
.. −
+++++++ += j
T
jjjj
T
jjj
K
j RHPHHPK
FK
SOLO
Kalman Filter Discrete Case – Innovation (continue – 3)
Assume i > j:
1,111112,111|11,1 +++++++++++++ +Φ−+= jijjjjjiii
T
jjjjii RRKFHHHPFH δ
{ } { } { } { } { }T
ji
T
j
T
jji
T
jiii
T
j
T
jjiii
T
ji vvEHxvEvxEHHxxEHE 111|111|111|1|1111
~~~~
++++++++++++++ +−−=ιι
( )1112,12,1, +++++++ −Φ== jjjjijjiji HKIFFFF
( ){ } 1,11111|11112,1 ++++++++++++ +−−Φ= jijjj
T
jjjjjjjii RRKHPHKIFH δ
{ [ ]}
1,11
1,1111|1111|112,1
+++
+++++++++++++
=
++−Φ=
jij
jijj
T
jjjjj
T
jjjjjii
R
RRHPHKHPFH
δ
δ
{ } 1,1111
..
+++++ = jij
K
T
ji RE
FK
διι { } 01 =+iE ι
Innovation =
White Noise for
Kalman Filter Gain!!!
&
Table of Content

58. 59
Kalman Filter
State Estimation in a Linear System (one cycle)
SOLO
State vector prediction111|111|
ˆˆ −−−−−− +Φ= kkkkkkk uGxx
Covariance matrix extrapolation111|111| −−−−−− +ΦΦ= k
T
kkkkkk QPP
Innovation Covariancek
T
kkkkk RHPHS += −1|
Gain Matrix Computation
1
1|
−
−= k
T
kkkk SHPK
Innovation
1|ˆ
1|
ˆ
−
−−=
kkz
kkkkk xHzi
Filteringkkkkkk iKxx += −1||
ˆˆ
Covariance matrix updating
( )
( ) ( ) T
kkk
T
kkkkkk
kkkk
T
kkkkk
kkkk
T
kkkkkkk
KRKHKIPHKI
PHKI
KSKP
PHSHPPP
+−−=
−=
−=
−=
−
−
−
−
−
−−
1|
1|
1|
1|
1
1|1||
1+= kk

59. 60
Kalman Filter
State Estimation in a Linear System (one cycle)
Sensor Data
Processing and
Measurement
Formation
Observation -
to - Track
Association
Input
Data Track Maintenance
( Initialization,
Confirmation
and Deletion)
Filtering and
Prediction
Gating
Computations
Samuel S. Blackman, " Multiple-Target Tracking with Radar Applications", Artech House,
1986
Samuel S. Blackman, Robert Popoli, " Design and Analysis of Modern Tracking Systems",
Artech House, 1999
SOLO
Rudolf E. Kalman
( 1920 - )

60. 61
1|1| ˆˆ: −− −=−= kkkkkkkk zzxHzi
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 18)
Innovation
The innovation is the quantity:
We found that:
{ } ( ){ } { } 0ˆ||ˆ| 1|1:11:11|1:1 =−=−= −−−−− kkkkkkkkkk zZzEZzzEZiE
[ ][ ]{ } { } k
T
kkkkkk
T
kkk
T
kkkkkk SHPHRZiiEZzzzzE =+==−− −−−−− :ˆˆ 1|1:11:11|1|
Using the smoothing property of the expectation:
{ }{ } ( ) ( ) ( ) ( )
( )
( ) ( ) { }xEdxxpxdxdyyxpx
dxdyypyxpxdyypdxyxpxyxEE
x
X
x y
YX
x y
yxp
YYX
y
Y
x
YX
YX
==








=










=





=
∫∫ ∫
∫ ∫∫ ∫
∞+
−∞=
∞+
−∞=
∞+
−∞=
∞+
−∞=
∞+
−∞=
∞+
−∞=
∞+
−∞=
,
||
,
,
||
,
  
{ } { }{ }1:1 −= k
T
jk
T
jk ZiiEEiiEwe have:
Assuming, without loss of generality, that k-1 ≥ j, and innovation I (j) is
Independent on Z1:k-1, and it can be taken outside the inner expectation:
{ } { }{ } { } 0
0
1:11:1 =








== −−
T
jkkk
T
jk
T
jk iZiEEZiiEEiiE


61. 62
1|1| ˆˆ: −− −=−= kkkkkkkk zzxHzi
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 18)
Innovation (continue – 1)
The innovation is the quantity:
We found that:
{ } ( ){ } { } 0ˆ||ˆ| 1|1:11:11|1:1 =−=−= −−−−− kkkkkkkkkk zZzEZzzEZiE
{ } k
T
kkkkkk
T
kk SHPHRZiiE =+= −− :1|1:1
{ } 0=
T
jk iiE
{ } jik
T
jk SiiE δ=
The uncorrelatedness property of the innovation implies that since they are Gaussian,
the innovation are independent of each other and thus the innovation sequence is
Strictly White.
Without the Gaussian assumption, the innovation sequence is Wide Sense White.
Thus the innovation sequence is zero mean and white for the Kalman (Optimal) Filter.
The innovation for the Kalman (Optimal) Filter extracts all the available information
from the measurement, leaving only zero-mean white noise in the measurement residual.

62. 63
kk
T
kn iSiz
1
:
2 −
=χ
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 19)
Innovation (continue – 2)
Define the quantity:
Let use: kkk iSu
2/1
:
−
=
Since is Gaussian (a linear combination of the nz components of )
is Gaussian too with:
ki ku ki
{ } { } 0:
0
2/1
==
−
 kkk iESuE { } { } { } z
k
nk
S
T
kkkk
T
kkk
T
kk ISiiESSiiSEuuE ===
−−−− 2/12/12/12/1
:

where Inz is the identity matrix of size nz. Therefore, since the covariance matrix of
u is diagonal, its components ui are uncorrelated and, since they are jointly Gaussian
they are also independent.
{ } ( )1,0;Pr:
1
22 1
ii
n
i
ik
T
kkk
T
kn uuuuuiSi
z
z
N==== ∑=
−
χ
Therefore is chi-square distributed with nz degrees of freedom.
2
znχ
Since Sk is symmetric and positive definite, it can be written as:
{ } 0,,& 1 >=== SiSSkn
H
kk
H
kkkk znz
diagDITTTDTS λλλ 
H
kkkk TDTS
11 −−
= { }2/12/1
1
2/12/12/1
,,&
−−−−−
==
znSSk
H
kkkk diagDTDTS λλ 

63. 64
SOLO Review of Probability
Chi-square Distribution
{ }( ) { }( ) x
T
x
T
ePexExPxExq
11
:
−−
=−−=
Assume a n-dimensional vector is Gaussian, with mean and covariance P, then
we can define a (scalar) random variable:
x { }xE
Since P is symmetric and positive definite, it can be written as:
{ } 0,,& 1 >=== PiPPPn
HH
P n
diagDITTTDTP λλλ 
H
P TDTP
11 −−
= { }2/12/1
1
2/12/12/1
,,&
−−−−−
== nPPP
H
P diagDTDTP λλ 
Since is Gaussian (a linear combination of the n components of )
is Gaussian too, with:
x u { }( )xEx −
{ } { }{ } 0:
0
2/1
=−=
−

xExEPuE { } { } { } n
P
T
xx
T
xx
T
IPeeEPPeePEuuE ===
−−−− 2/12/12/12/1
:

where In is the identity matrix of size n. Therefore, since the covariance matrix of
u is diagonal, its components ui are uncorrelated and, since they are jointly Gaussian
they are also independent.
{ } ( )1,0;Pr:
1
21
ii
n
i
i
T
x
T
x uuuuuePeq N==== ∑=
−
Therefore q is chi-square distributed with n degrees of freedom.
Let use: { }( ) xePxExPu 2/12/1
: −−
=−=

64. 65
SOLO Review of Probability
Derivation of Chi and Chi-square Distributions
Given k normal random independent variables X1, X2,…,Xk with zero men values and
same variance σ2
, their joint density is given by
( )
( ) ( ) 




 ++
−=






−
= ∏
=
2
22
1
2/
1
2/1
2
2
1
2
exp
2
1
2
2
exp
,,1
σσπσπ
σ k
kk
k
i
i
normal
tindependen
kXX
xx
x
xxp k


Define
Chi-square 0::
22
1
2
≥++== kk
xxy χ
Chi 0:
22
1
≥++= kk
xx χ
( ) 



 +≤++≤=Χ kkkkkk
dxxdp k
χχχχχ
22
1
Pr 
The region in χk space, where pΧk
(χk) is constant, is a hyper-shell of a volume
(A to be defined)
χχ dAVd k 1−
=
( )
( ) 

Vd
kk
kkkkkkkk
dAdxxdp k
χχ
σ
χ
σπ
χχχχχ 1
2
2
2/
22
1
2
exp
2
1
Pr −
Χ 





−=



 +≤++≤=
( )
( ) 





−=
−
Χ 2
2
2/
1
2
exp
2 σ
χ
σπ
χ
χ k
kk
k
k
A
p k
Compute
1x
2x
3x
χ
χdχχπ ddV 2
4=

65. 66
SOLO Review of Probability
Derivation of Chi and Chi-square Distributions (continue – 1)
( )
( )
( )k
k
kk
k
k U
A
p k
χ
σ
χ
σπ
χ
χ 





−=
−
Χ 2
2
2/
1
2
exp
2
Chi-square 0:
22
1
2
≥++== kk
xxy χ
( ) ( ) ( ) ( ) ( )
( )





<
≥





−
=








−+==
−
Χ
00
0
2
exp
22
1 2
2/1
2/
0
2
2
2
y
y
y
y
y
A
ypyp
d
yd
ypp
k
kk
y
k
Yk kkk
σσπ
χ
χ χχ


A is determined from the condition ( ) 1=∫
∞
∞−
dyypY
( )
( ) ( )
( ) ( )
( )2/
2
12/
222
exp
22
2/
2/2
0
2
2
2
22/
k
Ak
Ay
d
yyA
dyyp
k
k
k
kY
Γ
=→=Γ=











−





= ∫∫
∞
−
∞
∞−
π
πσσσπ
( ) ( )
( )
( )
( )yU
yy
k
kyp
kk
Y 





−





Γ
=
−
2
2/2
2
2/
2
exp
2/
2/1
,;
σσ
σ
Γ is the gamma function ( ) ( )∫
∞
−
−=Γ
0
1
exp dttta a
( ) ( ) ( )
( )
( )k
k
k
k
k
k
k
U
k
p k
χ
σ
χ
σ
χ
χ 







−
Γ
=
−−−
Χ 2
212/2
2
exp
2/
2/1
( )



<
≥
=
00
01
:
a
a
aU
Function of
One Random
Variable

66. 67
SOLO Review of Probability
Derivation of Chi and Chi-square Distributions (continue – 2)
Chi-square 0:
22
1
2
≥++== kk
xxy χ
Mean Value { } { } { }2 2 2 2
1k kE E x E x kχ σ= + + =
{ }
( ){ } ( ){ }
4
2 42 2 4
0
1, ,
& 3
th
i
i i
Moment of a
Gauss Distribution
x i i i i
x E x
i k
E x x E x xσ σ σ
 = =

=
 = − = − =


( ){ } ( ){ }
{ } { }
( )
( )
2
4
2 4
2
2 22 2 2 2 2 4 2 2 4
1
2 2 2 4 4 2 2 2 4
1 1 1 1 1
3
2 2 4 4
3 2
k
k
k k i
i
k k k k k
i j i i j
i j i i j
i j
k k
E k E k E x k
E x x k E x E x x k
k k k k k
χ
σ
σ
σ χ σ χ σ σ
σ σ
σ σ
=
= = = = =
≠
−
   
= − = − = −  ÷
   
    
= − = + −  ÷ ÷
    
= + − − =
∑
∑ ∑ ∑ ∑∑

Variance ( ){ }2
22 2 2 4
2
k
kE k kχ
σ χ σ σ= − =
where xi
are Gaussian
with
Gauss’ Distribution

67. 68
SOLO Review of Probability
Derivation of Chi and Chi-square Distributions (continue – 3)
Tail probabilities of the chi-square and normal densities.
The Table presents the points on the chi-square
distribution for a given upper tail probability
{ }xyQ >= Pr
where y = χn
2
and n is the number of degrees
of freedom. This tabulated function is also
known as the complementary distribution.
An alternative way of writing the previous
equation is: { } ( )QxyQ n −=≤=− 1Pr1
2
χ
which indicates that at the left of the point x
the probability mass is 1 – Q. This is
100 (1 – Q) percentile point.
Examples
1. The 95 % probability region for χ2
2
variable
can be taken at the one-sided probability
region (cutting off the 5% upper tail): ( )[ ] [ ]99.5,095.0,0
2
2 =χ
.5 99
2. Or the two-sided probability region (cutting off both 2.5% tails): ( ) ( )[ ] [ ]38.7,05.0975.0,025.0
2
2
2
2 =χχ
.0 51
.0 975 .0 025.0 05
.7 38
3. For χ1002 variable, the two-sided 95% probability region (cutting off both 2.5% tails) is:
( ) ( )[ ] [ ]130,74975.0,025.0
2
100
2
100 =χχ
74
130

68. 69
SOLO Review of Probability
Derivation of Chi and Chi-square Distributions (continue – 4)
Note the skewedness of the chi-square
distribution: the above two-sided regions are
not symmetric about the corresponding means
{ } nE n =
2
χ
Tail probabilities of the chi-square and normal densities.
For degrees of freedom above 100, the
following approximation of the points on the
chi-square distribution can be used:
( ) ( )[ ]22
121
2
1
1 −+−=− nQQn Gχ
where G ( ) is given in the last line of the Table
and shows the point x on the standard (zero
mean and unity variance) Gaussian distribution
for the same tail probabilities.
In the case Pr { y } = N (y; 0,1) and with
Q = Pr { y>x }, we have x (1-Q) :=G (1-Q)
.5 99.0 51
.0 975 .0 025.0 05
.7 38

69. 70
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 19)
Innovation (continue – 2)
Table of Content
The fact that the innovation sequence is zero mean and white for the Kalman (Optimal)
Filter, is very important and can be used in Tracking Systems:
1. when a single target is detected with probability 1 (no false alarms), the innovation
can be used to check Filter Consistency (in fact the knowledge of Filter Parameters
Φ (k), G (k), H (k) – target model, Q (k), R (k) – system and measurement noises)
2. when a single target is detected with probability 1 (no false alarms), and the
target initiate a unknown maneuver (change model) at an unknown time
the innovation can be used to detect the start of the maneuver (change of target model)
by detecting a Filter Inconsistency and choose from a bank of models (see IMM method)
(Φi (k), Gi (k), Hi (k) –i=1,…,n target models) the one with a white innovation.
3. when a single target is detected with probability less then 1 and false alarms are
also detected, the innovation can be used to provide information of the probability
of each detection to be the real target (providing Gating capability that eliminates
less probable detections) (see PDAF method).
4. when multiple targets are detected with probability less then 1 and false alarms are
also detected, the innovation can be used to provide Gating information for each
target track and probability of each detection to be related to each track (data
association). This is done by running a Kalman Filter for each initiated track.
(see JPDAF and MTT methods)

70. 71
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 20)
Evaluation of Kalman Filter Consistency
A state-estimator (filter) is called consistent if its state estimation error satisfy
( ) ( ){ } ( ){ } 0|~:|ˆ ==− kkxEkkxkxE
( ) ( )[ ] ( ) ( )[ ]{ } ( ) ( ){ } ( )kkPkkxkkxEkkxkxkkxkxE TT
||~|~:|ˆ|ˆ ==−−
this is a finite-sample consistency property, that is, the estimation errors based on a
finite number of samples (measurements) should be consistent with the theoretical
statistical properties:
• Have zero mean (i.e. the estimates are unbiased).
• Have covariance matrix as calculated by the Filter.
The Consistency Criteria of a Filter are:
1. The state errors should be acceptable as zero mean and have magnitude commensurate
with the state covariance as yielded by the Filter.
2. The innovation should have the same property as in (1).
3. The innovation should be white noise.
Only the last two criteria (based on innovation) can be tested in real data applications.
The first criterion, which is the most important, can be tested only in simulations.

71. 72
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 21)
Evaluation of Kalman Filter Consistency (continue – 1)
When we design the Kalman Filter, we can perform Monte Carlo (N independent runs)
Simulations to check the Filter Consistency (expected performances).
Real time (Single-Run Tests)
In Real Time, we can use a single run (N = 1). In this case the simulations are replaced
by assuming that we can replace the Ensemble Averages (of the simulations) by the
Time Averages based on the Ergodicity of the Innovation and perform only the tests
(2) and (3) based on Innovation properties.
The Innovation bias and covariance can be evaluated using
( ) ( ) ( )∑∑ == −
==
K
k
T
K
k
kiki
K
Ski
K
i
11 1
1ˆ&
1ˆ

72. 73
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 22)
Evaluation of Kalman Filter Consistency (continue – 2)
Real time (Single-Run Tests) (continue – 1)
Test 2: ( ) ( ){ } ( ){ } ( ) ( ){ } ( )kSkikiEkiEkkzkzE T
===−− &0:1|ˆ
Using the Time-Average Normalized Innovation
Squared (NIS) statistics
( ) ( ) ( )∑=
−
=
K
k
T
i kikSki
K 1
11
:ε
must have a chi-square distribution with
K nz degrees of freedom.
iK ε
Tail probabilities of the chi-square and normal densities.
The test is successful if [ ]21,rri ∈ε
where the confidence interval [r1,r2] is defined
using the chi-square distribution of iε
[ ]{ } αε −=∈ 1,Pr 21 rri
For example for K=50, nz=2, and α=0.05, using the two
tails of the chi-square distribution we get
( )
( )



==→=
==→=
→
6.250/130130925.0
5.150/7474025.0
~50
2
2
100
1
2
1002
100
r
r
i
χ
χ
χε
.0 975
.0 025
74
130

73. 74
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 23)
Evaluation of Kalman Filter Consistency (continue – 3)
Real time (Single-Run Tests) (continue – 2)
Test 3: Whiteness of Innovation
Use the Normalized Time-Average Autocorrelation
( ) ( ) ( ) ( ) ( ) ( ) ( )
2/1
111
:
−
===






+++= ∑∑∑
K
k
T
K
k
T
K
k
T
i lkilkikikilkikilρ
In view of the Central Limit Theorem, for large K, this statistics is normal distributed.
For l≠0 the variance can be shown to be 1/K that tends to zero for large K.
Denoting by ξ a zero-mean unity-variance normal
random variable, let r1 such that
[ ]{ } αξ −=−∈ 1,Pr 11 rr
For α=0.05, will define (from the normal distribution)
r1 = 1.96. Since has standard deviation of
The corresponding probability region for α=0.05 will
be [-r, r] where
iρ K/1
KKrr /96.1/1 ==
Normal Distribution

74. 75
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 24)
Evaluation of Kalman Filter Consistency (continue – 4)
Monte-Carlo Simulation Based Tests
The tests will be based on the results of Monte-Carlo Simulations (Runs) that provide
N independent samples
( ) ( ) ( ) ( ) ( ) ( ){ } NikkxkkxEkkPkkxkxkkx
T
iiiii ,,1|~|~|&|ˆ:|~ ==−=
Test 1:
For each run i we compute at each scan k
And compute the Normalized (state) Estimation Error Squared (NEES)
( ) ( ) ( ) ( ) NikkxkkPkkxk i
T
ixi ,,1|~||~: 1
== −
ε
Under the Hypothesis that the Filter is Consistent and the Linear Gaussian,
is chi-square distributed with nx (dimension of x) degrees of freedom.
Then
( )kxiε
( ){ } xxi nkE =ε
The average, over N runs, of is( )kxiε
( ) ( )∑=
=
N
i
xix k
N
k
1
1
: εε

75. 76
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 25)
Evaluation of Kalman Filter Consistency (continue – 5)
Monte-Carlo Simulation Based Tests (continue – 1)
Test 1 (continue – 1):
The average, over N runs, of is( )kxiε
( ) ( )∑=
=
N
i
xix k
N
k
1
1
: εε
The test is successful if [ ]21,rrx ∈ε
where the confidence interval [r1,r2] is defined
using the chi-square distribution of iε
[ ]{ } αε −=∈ 1,Pr 21 rrx
For example for N=50, nx=2, and α=0.05, using the two
tails of the chi-square distribution we get
( )
( )



==→=
==→=
→
6.250/130130925.0
5.150/7474025.0
~50
2
2
100
1
2
1002
100
r
r
i
χ
χ
χε
Tail probabilities of the chi-square and normal densities.
.0 975
.0 025
74
130
must have a chi-square distribution with
N nx degrees of freedom.
xN ε

76. 77
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 26)
Evaluation of Kalman Filter Consistency (continue – 6)
Monte-Carlo Simulation Based Tests (continue – 2)
The test is successful if [ ]21,rri ∈ε
where the confidence interval [r1,r2] is defined
using the chi-square distribution of iε
[ ]{ } αε −=∈ 1,Pr 21 rri
For example for N=50, nz=2, and α=0.05, using the two
tails of the chi-square distribution we get
( )
( )



==→=
==→=
→
6.250/130130925.0
5.150/7474025.0
~50
2
2
100
1
2
1002
100
r
r
i
χ
χ
χε
Tail probabilities of the chi-square and normal densities.
.0 975
.0 025
74
130
must have a chi-square distribution with
N nz degrees of freedom.
iN ε
Test 2: ( ) ( ){ } ( ){ } ( ) ( ){ } ( )kSkikiEkiEkkzkzE T
===−− &0:1|ˆ
Using the Normalized Innovation Squared (NIS)
statistics, compute from N Monte-Carlo runs:
( ) ( ) ( ) ( )∑=
−
=
N
j
jj
T
ji kikSki
N
k
1
11
:ε

77. 78
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 27)
Evaluation of Kalman Filter Consistency (continue – 7)
Test 3: Whiteness of Innovation
Use the Normalized Sample Average Autocorrelation
( ) ( ) ( ) ( ) ( ) ( ) ( )
2/1
111
:,
−
===






= ∑∑∑
N
j
j
T
j
N
j
j
T
j
N
j
j
T
ji mimikikimikimkρ
In view of the Central Limit Theorem, for large N, this statistics is normal distributed.
For k≠m the variance can be shown to be 1/N that tends to zero for large N.
Denoting by ξ a zero-mean unity-variance normal
random variable, let r1 such that
[ ]{ } αξ −=−∈ 1,Pr 11 rr
For α=0.05, will define (from the normal distribution)
r1 = 1.96. Since has standard deviation of
The corresponding probability region for α=0.05 will
be [-r, r] where
iρ N/1
NNrr /96.1/1 ==
Normal Distribution
Monte-Carlo Simulation Based Tests (continue – 3)

78. 79
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 28)
Evaluation of Kalman Filter Consistency (continue – 8)
Examples Bar-Shalom, Y, Li, X-R, “Estimation and Tracking: Principles, Techniques
and Software”, Artech House, 1993, pg.242
Monte-Carlo Simulation Based Tests (continue – 4)
Single Run, 95% probability
[ ]99.5,0∈xεTest (a) Passes if
A one-sided region is considered.
For nx = 2 we have
( ) ( )[ ] [ ]99.5,095.0,02 2
2
2
2 == χχxn
( ) ( ) ( ) ( )∑=
−
=
K
k
T
x kkxkkPkkx
K
k
1
1
|~||~1
:ε
( ) ( ) ( ) qkxkkx +−Φ= 1
See behavior of for various values of the process noise q
for filters that are perfectly matched.

79. 80
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 29)
Evaluation of Kalman Filter Consistency (continue – 9)
Examples Bar-Shalom, Y, Li, X-R, “Estimation and Tracking: Principles, Techniques
and Software”, Artech House, 1993, pg.244
Monte-Carlo Simulation Based Tests (continue – 5)
Monte-Carlo, N=50, 95% probability
[ ] [ ]6.2,5.150/130,50/74 =∈xεTest (a) Passes if
( ) ( ) ( ) ( )∑=
−
=
N
j
jj
T
jx kkxkkPkkx
N
k
1
1
|~||~1
:ε(a)
( ) ( ) ( ) ( ) ( ) ( ) ( )
2/1
111
:,
−
===






= ∑∑∑
N
j
j
T
j
N
j
j
T
j
N
j
j
T
ji mimikikimikimkρ(c)
The corresponding probability region for
α=0.05 will be [-r, r] where
28.050/96.1/1 === Nrr
[ ] [ ]43.1,65.050/4.71,50/3.32 =∈iεTest (b) Passes if
( ) ( ) ( ) ( )∑=
−
=
N
j
jj
T
ji kikSki
N
k
1
11
:ε(b)
( ) ( )[ ] [ ]130,74925.0,025.02 2
100
2
100 == χχxn
( ) ( )[ ] [ ]71,32925.0,025.01 2
100
2
100 == χχzn

80. 81
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 30)
Evaluation of Kalman Filter Consistency (continue – 10)
Examples Bar-Shalom, Y, Li, X-R, “Estimation and Tracking: Principles, Techniques
and Software”, Artech House, 1993, pg.245
Monte-Carlo Simulation Based Tests (continue – 6)
Example Mismatched Filter
A Mismatched Filter is tested: Real System Process Noise q = 9 Filter Model Process Noise qF=1
( ) ( ) ( ) ( )∑=
−
=
K
k
T
x kkxkkPkkx
K
k
1
1
|~||~1
:ε
( ) ( ) ( ) qkxkkx +−Φ= 1
(1) Single Run
(2) A N=50 runs Monte-Carlo with the
95% probability region
( ) ( ) ( ) ( )∑=
−
=
N
j
jj
T
jx kkxkkPkkx
N
k
1
1
|~||~1
:ε
[ ] [ ]6.2,5.150/130,50/74 =∈xεTest (2) Passes if
( ) ( )[ ] [ ]130,74925.0,025.02 2
100
2
100 == χχxn
Test Fails
Test Fails
[ ]99.5,0∈xεTest (1) Passes if
( ) ( )[ ] [ ]99.5,095.0,02 2
2
2
2 == χχxn

81. 82
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 31)
Evaluation of Kalman Filter Consistency (continue – 11)
Examples Bar-Shalom, Y, Li, X-R, “Estimation and Tracking: Principles, Techniques
and Software”, Artech House, 1993, pg.246
Monte-Carlo Simulation Based Tests (continue – 7)
Example Mismatched Filter (continue -1)
A Mismatched Filter is tested: Real System Process Noise q = 9 Filter Model Process Noise qF=1
( ) ( ) ( ) qkxkkx +−Φ= 1
(3) A N=50 runs Monte-Carlo with the
95% probability region
(4) A N=50 runs Monte-Carlo with the
95% probability region
( ) ( ) ( ) ( )∑=
−
=
N
j
jj
T
ji kikSki
N
k
1
11
:ε
[ ] [ ]43.1,65.050/4.71,50/3.32 =∈iεTest (3) Passes if
( ) ( )[ ] [ ]71,32925.0,025.01 2
100
2
100 == χχzn
( ) ( ) ( ) ( ) ( ) ( ) ( )
2/1
111
:,
−
===






= ∑∑∑
N
j
j
T
j
N
j
j
T
j
N
j
j
T
ji mimikikimikimkρ
(c)
The corresponding probability region for
α=0.05 will be [-r, r] where
28.050/96.1/1 === Nrr
Test Fails
Test Fails

82. 83
Extended Kalman Filter
Sensor Data
Processing and
Measurement
Formation
Observation -
to - Track
Association
Input
Data Track Maintenance
( Initialization,
Confirmation
and Deletion)
Filtering and
Prediction
Gating
Computations
Samuel S. Blackman, " Multiple-Target Tracking with Radar Applications", Artech House,
1986
Samuel S. Blackman, Robert Popoli, " Design and Analysis of Modern Tracking Systems",
Artech House, 1999
SOLO
In the extended Kalman filter, (EKF) the state
transition and observation models need not be linear
functions of the state but may instead be (differentiable)
functions.
( ) ( ) ( )[ ] ( )kwkukxkfkx +=+ ,,1
( ) ( ) ( )[ ] ( )11,1,11 +++++=+ kkukxkhkz ν
State vector dynamics
Measurements
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ){ } lklekeE
T
vw ,0 ∀=



=
≠
=
lk
lk
lk
1
0
,δ
The function f can be used to compute the predicted state from the previous estimate
and similarly the function h can be used to compute the predicted measurement from
the predicted state. However, f and h cannot be applied to the covariance directly.
Instead a matrix of partial derivatives (the Jacobian) is computed.
( ) ( ) ( )[ ] ( ){ } ( )[ ] ( )
( ){ }
( ) ( )
( ){ }
( ) ( )keke
x
f
keke
x
f
kekukxEkfkukxkfke wx
Hessian
kxE
T
xx
Jacobian
kxE
wx ++
∂
∂
+
∂
∂
=+−=+ 

2
2
2
1
,,,,1
( ) ( ) ( )[ ] ( ){ } ( )[ ] ( )
( ){ }
( ) ( )
( ){ }
( ) ( 111
2
1
111,1,11,1,11
1
2
2
1
++++
∂
∂
+++
∂
∂
=+++++−+++=+
++
kke
x
h
keke
x
h
kkukxEkhkukxkhke x
Hessian
kxE
T
xx
Jacobian
kxE
z νν 

Taylor’s Expansion:

83. 84
Extended Kalman Filter
State Estimation (one cycle)
SOLO
( )11|11| ,ˆ,1ˆ −−−− −= kkkkk uxkfx
State vector prediction
Jacobians Computation
1|1|1 ˆˆ
1 &
−−−
∂
∂
=
∂
∂
=Φ −
kkkk x
k
x
k
x
h
H
x
f
Covariance matrix extrapolation111|111| −−−−−− +ΦΦ= k
T
kkkkkk QPP
Innovation Covariancek
T
kkkkk RHPHS += −1|
Gain Matrix Computation
1
1|
−
−= k
T
kkkk SHPK
Innovation
1|ˆ
1|
ˆ
−
−−=
kkz
kkkkk xHzi
Filteringkkkkkk iKxx += −1||
ˆˆ
Covariance matrix updating
( )
( ) ( ) T
kkk
T
kkkkkk
kkkk
T
kkkkk
kkkk
T
kkkkkkk
KRKHKIPHKI
PHKI
KSKP
PHSHPPP
+−−=
−=
−=
−=
−
−
−
−
−
−−
1|
1|
1|
1|
1
1|1||
1+= kk

84. 85
Extended Kalman Filter
State Estimation (one cycle)
Sensor Data
Processing and
Measurement
Formation
Observation -
to - Track
Association
Input
Data Track Maintenance
( Initialization,
Confirmation
and Deletion)
Filtering and
Prediction
Gating
Computations
Samuel S. Blackman, " Multiple-Target Tracking with Radar Applications", Artech House,
1986
Samuel S. Blackman, Robert Popoli, " Design and Analysis of Modern Tracking Systems",
Artech House, 1999
SOLO
Rudolf E. Kalman
( 1920 - )

85. 86
Unscented Kalman FilterSOLO
Criticism of the Extended Kalman Filter
Unlike its linear counterpart, the extended Kalman filter is not an optimal estimator.
In addition, if the initial estimate of the state is wrong, or if the process is modeled
incorrectly, the filter may quickly diverge, owing to its linearization. Another problem
with the extended Kalman filter is that the estimated covariance matrix tends to
underestimate the true covariance matrix and therefore risks becoming inconsistent
in the statistical sense without the addition of "stabilising noise".
Having stated this, the extended Kalman filter can give reasonable performance, and
is arguably the de facto standard in navigation systems and GPS.

86. 87
Uscented Kalman FilterSOLO
When the state transition and observation models – that is, the predict and update
functions f and h (see above) – are highly non-linear, the extended Kalman filter can
give particularly poor performance [JU97]. This is because only the mean is
propagated through the non-linearity. The unscented Kalman filter (UKF) [JU97]
uses a deterministic sampling technique known as the to pick a minimal set of
sample points (called sigma points) around the mean. These sigma points are then
propagated through the non-linear functions and the covariance of the estimate is
then recovered. The result is a filter which more accurately captures the true mean
and covariance. (This can be verified using Monte Carlo sampling or through a
Taylor series expansion of the posterior statistics.) In addition, this technique
removes the requirement to analytically calculate Jacobians, which for complex
functions can be a difficult task in itself.
( ) ( ) ( )[ ] ( )kwkukxkfkx +=+ ,,1
( ) ( )[ ] ( )11,11 ++++=+ kkxkhkz ν
State vector dynamics
Measurements
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ){ } lklekeE
T
vw ,0 ∀=



=
≠
=
lk
lk
lk
1
0
,δ
The Unscent Algorithm using ( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
Determines ( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkzEkzke z
T
zzz =−= &:

87. 88
Unscented Kalman FilterSOLO
( ) ( )[ ]
( )
n
n
j j
j
n
x
n
x
n
x
x
x
xx
fx
n
xxf








∂
∂
=∇⋅
∇⋅=+
∑
∑
=
∞
=
1
0
ˆ
:
!
1
ˆ
δδ
δδ
Develop the nonlinear function f in a Taylor series
around
xˆ
Define also the operator ( )[ ] ( )xf
x
xfxfD
n
n
j j
jx
n
x
n
x
x








∂
∂
=∇⋅= ∑=1
: δδδ
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function .( )xfy =
Let compute
Assume is a random variable with a probability density function pX (x) (known or
unknown) with mean and covariance
x
{ } ( ) ( ){ }Txx
xxxxEPxEx ˆˆ,ˆ −−==
( ){ } { }
( )[ ]{ } ∑ ∑∑
∑
∞
= =
∞
=
∞
=
























∂
∂
=∇⋅=
=+=
0
ˆ
10
ˆ
0
!
1
!
1
!
1
ˆˆ
n
x
n
n
j j
j
n
x
n
x
n
n
x
f
x
xE
n
fxE
n
DE
n
xxfEy
x
δδ
δ δ
{ } { }
{ } ( )( ){ } xxTT
PxxxxExxE
xxExE
xxx
=−−=
=−=
+=
ˆˆ
0ˆ
ˆ
δδ
δ
δ

88. 89
Unscented Kalman Filter
SOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function .
(continue – 1)
( )xfy =
{ } { }
{ } ( )( ){ } xxTT
PxxxxExxE
xxExE
xxx
=−−=
=−=
+=
ˆˆ
0ˆ
ˆ
δδ
δ
δ
( ){ } ( )
+
























∂
∂
+
























∂
∂
+
























∂
∂
+
























∂
∂
+=
























∂
∂
=+=
∑∑∑
∑∑ ∑
===
=
∞
= =
x
n
j j
jx
n
j j
jx
n
j j
j
x
n
j j
j
n
x
n
n
j j
j
f
x
xEf
x
xEf
x
xE
f
x
xExff
x
xE
n
xxfEy
xxx
xx
ˆ
4
1
ˆ
3
1
ˆ
2
1
ˆ
10
ˆ
1
!4
1
!3
1
!2
1
ˆ
!
1
ˆˆ
δδδ
δδδ
Since all the differentials of f are computed around the mean (non-random)xˆ
( )[ ]{ } ( )[ ]{ } { }( )[ ] ( )[ ]xx
xxT
xxx
TT
xxx
TT
xxx fPfxxEfxxEfxE ˆˆˆˆ
2
∇∇=∇∇=∇∇=∇⋅ δδδδδ
( )[ ]{ } { } { } 0
ˆ
1
0ˆ
1
ˆ0
ˆ =
















∂
∂
=
























∂
∂
=
















∇⋅=∇⋅ ∑∑ ==
x
n
j j
j
x
n
j j
j
x
xxx f
x
xEf
x
xEfxEfxE
xx

δδδδ
( ){ } [ ]{ } ( ) ( )[ ] [ ]{ } [ ]{ } +++∇∇+==+= ∑
∞
=
xxxxxx
xxT
x
n
x
n
x fDEfDEfPxffDE
n
xxfEy ˆ
4
ˆ
3
ˆ
0
ˆ
!4
1
!3
1
!2
1
ˆ
!
1
ˆˆ δδδδ

89. 90
Simon J. Julier
Unscented Kalman FilterSOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function .
(continue - 2)
( )xfy = { } { }
{ } ( )( ){ } xxTT
PxxxxExxE
xxExE
xxx
=−−=
=−=
+=
ˆˆ
0ˆ
ˆ
δδ
δ
δ
Unscented Transformation (UT), proposed by Julier and Uhlmann
uses a set of “sigma points” to provide an approximation of
the probabilistic properties through the nonlinear function
Jeffrey K. Uhlman
A set of “sigma points” S consists of p+1 vectors and their associated
weights S = { i=0,1,..,p: x(i)
, W(i)
}.
(1) Compute the transformation of the “sigma points” through the
nonlinear transformation f:
( ) ( )
( ) pixfy ii
,,1,0 ==
(2) Compute the approximation of the mean: ( ) ( )
∑=
≈
p
i
ii
yWy
0
ˆ
The estimation is unbiased if:
( ) ( ) ( ) ( )
{ } ( )
yWyyEWyWE
p
i
i
p
i
y
ii
p
i
ii
ˆˆ
00
ˆ
0
===






∑∑∑ ===

( )
1
0
=∑=
p
i
i
W
(3) The approximation of output covariance is given by
( ) ( )
( ) ( )
( )∑=
−−≈
p
i
Tiiiyy
yyyyWP
0
ˆˆ

90. 91
Unscented Kalman FilterSOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function (continue – 3)( )xfy =
One set of points that satisfies the above conditions consists of a symmetric set of symmetric
p = 2nx points that lie on the covariance contour Pxx
:
th
xn
( ) ( )
( )
( )
( )
( ) ( )
( )
( ) ( )
x
x
ni
x
i
xxxni
i
xxxi
ni
nWW
nWW
P
W
n
xx
P
W
n
xx
WWxx
x
x
,,1
2/1
2/1
1
ˆ
1
ˆ
ˆ
0
0
0
0
0
00
=











−=
−=








−
−=








−
+=
==
+
+
where is the row or column of the matrix square root of nx Pxx
/(1-W0)
(the original covariance matrix Pxx
multiplied by the number of dimensions of x, nx/(1-W0)).
This implies:
( )( )i
xx
x WPn 01/ −
xxx
n
i
T
i
xxx
i
xxx
P
W
n
P
W
n
P
W
nx
01 00 111 −
=







−







−
∑=
Unscented Transformation (UT) (continue – 1)

91. 92
Unscented Kalman Filter
SOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function (continue – 3)( )xfy =
Unscented Transformation (UT) (continue – 2)
( ) ( )
( )
( )
( )
( )








+=
=
=
==
∑
∑
∞
=
−
∞
=
0
0
2,,1ˆ
!
1
,,1ˆ
!
1
0ˆ
n
xx
n
x
n
x
n
x
ii
nnixfD
n
nixfD
n
ixf
xfy
i
i


δ
δ
1
2
Unscented Algorithm:
( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )∑∑
∑
∑ ∑∑ ∑∑
==
=
=
∞
=
−
=
∞
==




++
−
+
−
+=




++++
−
+=
−
+
−
+==
x
ii
x
i
x
iii
x
i
x
i
x
n
i
xx
x
n
i
x
x
n
i
xxx
x
n
i n
n
x
x
n
i n
n
x
x
n
i
ii
UT
xfDxfD
n
W
xfD
n
W
xf
xfDxfDxfDxf
n
W
xfW
xfD
nn
W
xfD
nn
W
xfWyWy
1
640
1
20
1
6420
0
1 0
0
1 0
0
0
2
0
ˆ
!6
1
ˆ
!4
11
ˆ
2
11
ˆ
ˆ
!6
1
ˆ
!4
1
ˆ
!2
1
ˆ
1
ˆ
ˆ
!
1
2
1
ˆ
!
1
2
1
ˆˆ


δδδ
δδδ
δδ
( )
i
xxx
i
i
P
W
n
xxxx 







−
±=±=
01
ˆˆ δ
Since ( ) ( )
( )
( )



−
=








∂
∂
−= ∑=
−
oddnxfD
evennxfD
xf
x
xxfD n
x
n
x
n
n
j j
ij
n
x
i
i
x
i
ˆ
ˆ
ˆˆ
1 δ
δ
δ δ

92. 93
Unscented Kalman Filter
( ) ( ) ( ) ( )∑=




++
−
+∇∇+=
x
ii
n
i
xx
x
xxT
UT xfDxfD
n
W
xfPxfy
1
640
ˆ
!6
1
ˆ
!4
11
ˆ
2
1
ˆˆ δδ
( )
i
xxx
i
i
P
W
n
xxxx 







−
±=±=
01
ˆˆ δ
SOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function (continue – 4)( )xfy =
Unscented Transformation (UT) (continue – 3)
Unscented Algorithm:
( ) ( )
( ) ( ) ( )xfPxfP
W
n
n
W
xfP
W
n
P
W
n
n
W
xfP
W
n
P
W
n
n
W
xfD
n
W
xxTxxxT
x
n
i
T
i
xxx
i
xxxT
x
n
i
T
i
xxx
i
xxxT
x
n
i
x
x
x
xx
i
ˆ
2
1
ˆ
12
11
ˆ
112
11
ˆ
112
11
ˆ
2
11
0
0
1 00
0
1 00
0
1
20
∇∇=∇





−
∇
−
=∇
















−







−
∇
−
=
∇







−







−
∇
−
=
−
∑
∑∑
=
==
δ
Finally:
We found
( ){ } [ ]{ } ( ) ( )[ ] [ ]{ } [ ]{ } +++∇∇+==+= ∑
∞
=
xxxxxx
xxT
x
n
x
n
x fDEfDEfPxffDE
n
xxfEy ˆ
4
ˆ
3
ˆ
0
ˆ
!4
1
!3
1
!2
1
ˆ
!
1
ˆˆ δδδδ
We can see that the two expressions agree exactly to the third order.

93. 94
Unscented Kalman Filter
SOLO
Propagating Means and Covariances Through Nonlinear Transformations
Consider a nonlinear function (continue – 5)( )xfy =
Unscented Transformation (UT) (continue – 4)
Accuracy of the Covariance:
( ) ( ){ } { }
( ) ( ) ( ) ( ) ( )
( ) ( )[ ] [ ]{ } [ ]{ }
( ) ( )[ ] [ ]{ } [ ]{ }
T
xxxxxx
xxT
x
xxxxxx
xxT
x
T
m
m
xx
n
n
xx
TTTyy
fDEfDEfPxf
fDEfDEfPxf
fD
m
xfDxffD
n
xfDxfE
yyyyEyyyyEP






+++∇∇+⋅
⋅





+++∇∇+−














++





++=
−=−−=
∑∑
∞
=
∞
=


ˆ
4
ˆ
3
ˆ
ˆ
4
ˆ
3
ˆ
22
!4
1
!3
1
!2
1
ˆ
!4
1
!3
1
!2
1
ˆ
!
1
ˆˆ
!
1
ˆˆ
ˆˆˆˆ
δδ
δδ
δδδδ
( ) ( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( )
( )




















+






++






++=
∑∑
∑∑
∞
=
∞
=
∞
=
∞
=
T
m
m
x
n
n
x
T
n
n
x
T
x
T
n
n
x
T
x
T
fD
m
fD
n
E
xfxfD
n
ExfxfDExfD
n
ExfxfDExfxfxf
22
2
0
2
0
!
1
!
1
ˆˆ
!
1
ˆˆˆ
!
1
ˆˆˆˆˆ
δδ
δδδδ


94. 95
Uscented Kalman FilterSOLO

95. 96
Uscented Kalman FilterSOLO
( ) ( )∑∑ −−==
N
T
iiiz
N
ii zzPz
2
0
2
0
ψψβψβ
x
xPα
xP




zP
( )f
iβ
iβ
iψ
z
{ } [ ]xxi PxPxx ααχ −+=
Weighted
sample mean
Weighted
sample
covariance
Table of Content

96. 97
Uscented Kalman Filter
SOLO
UKF Summary
Initialization of UKF
{ } ( ) ( ){ }T
xxxxEPxEx 00000|000
ˆˆˆ −−==
{ } [ ] ( )( ){ }










=−−===
R
Q
P
xxxxEPxxEx
TaaaaaTTaa
00
00
00
ˆˆ00ˆˆ
0|0
00000|0000
[ ]TTTTa
vwxx =:
For { }∞∈ ,,1 k
Calculate the Sigma Points ( )
( )
λγ
γ
γ +=







=−=
=+=
=
−−−−
+
−−
−−−−−−
−−−−
L
LiPxx
LiPxx
xx
i
kkkk
Li
kk
i
kkkk
i
kk
kkkk
,,1ˆˆ
,,1ˆˆ
ˆˆ
1|11|11|1
1|11|11|1
1|1
0
1|1


State Prediction and its Covariance
System Definition
( ) { } { }
( ) { } { }



==+=
==+−= −−−−−−−
lkk
T
lkkkkk
lkk
T
lkkkkkk
RvvEvEvxkhz
QwwEwEwuxkfx
,
,1111111
&0,
&0,,1
δ
δ
( ) Liuxkfx k
i
kk
i
kk 2,,1,0,ˆ,1ˆ 11|11| =−= −−−−
( ) ( ) ( )
( )
Li
L
W
L
WxWx m
i
m
L
i
i
kk
m
ikk 2,,1
2
1
&ˆˆ 0
2
0
1|1| =
+
=
+
== ∑=
−−
λλ
λ
0
1
2
( )
( )( ) ( ) ( )
( )
Li
L
W
L
WxxxxWP c
i
c
L
i
T
kk
i
kkkk
i
kk
c
ikk 2,,1
2
1
&1ˆˆˆˆ 2
0
2
0
1|1|1|1|1| =
+
=+−+
+
=−−= ∑=
−−−−−
λ
βα
λ
λ

97. 98
Uscented Kalman Filter
SOLO
UKF Summary (continue – 1)
Measure Prediction
( ) Lixkhz i
kk
i
kk 2,,1,0ˆ,ˆ 1|1| == −−
( ) ( ) ( )
( )
Li
L
W
L
WzWz m
i
m
L
i
i
kk
m
ikk 2,,1
2
1
&ˆˆ 0
2
0
1|1| =
+
=
+
== ∑=
−−
λλ
λ
3
Innovation and its Covariance4
1|ˆ −−= kkkk zzi
( )
( )( ) ( ) ( )
( )
Li
L
W
L
WzzzzWPS c
i
c
L
i
T
kk
i
kkkk
i
kk
c
i
zz
kkk 2,,1
2
1
&1ˆˆˆˆ 2
0
2
0
1|1|1|1|1| =
+
=+−+
+
=−−== ∑=
−−−−−
λ
βα
λ
λ
Kalman Gain Computations5
( )
( )( ) ( ) ( )
( )
Li
L
W
L
WzzxxWP c
i
c
L
i
T
kk
i
kkkk
i
kk
c
i
xz
kk 2,,1
2
1
&1ˆˆˆˆ 2
0
2
0
1|1|1|1|1| =
+
=+−+
+
=−−= ∑=
−−−−−
λ
βα
λ
λ
1
1|1|
−
−−= zz
kk
xz
kkk PPK
Update State and its Covariance6
kkkkkk iKxx += −1||
ˆˆ
T
kkkkkkk KSKPP −= −1||
k = k+1 & return to 1

98. 99
Unscented Kalman Filter
State Estimation (one cycle)
Sensor Data
Processing and
Measurement
Formation
Observation -
to - Track
Association
Input
Data Track Maintenance
( Initialization,
Confirmation
and Deletion)
Filtering and
Prediction
Gating
Computations
Samuel S. Blackman, " Multiple-Target Tracking with Radar Applications", Artech House,
1986
Samuel S. Blackman, Robert Popoli, " Design and Analysis of Modern Tracking Systems",
Artech House, 1999
SOLO
Simon J. Julier Jeffrey K. Uhlman

99. 100
Estimators
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )kkvkkv
kvkxkHkz
kwkkukGkxkkx
ξ+Ψ=+
+=
Γ++Φ=+
1
1
SOLO
Kalman Filter Discrete Case & Colored Measurement Noise
Assume a discrete dynamic system
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
kRlekeEkvEkvke ,
0
&: δξξξ =−=

( ) ( ){ } { }0=lekeE
T
w ξ



=
≠
=
lk
lk
lk
1
0
,δ
Solution
Define a new “pseudo-measurement”:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]kvkxkHkkvkxkHkzkkzk +Ψ−++++=Ψ−+= 1111:ζ
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) ( ) ( )
( )
( ) ( ) ( )kxkHkkvkkvkwkkukGkxkkH
k
Ψ−Ψ−++Γ++Φ+=
  
ξ
11
( ) ( ) ( ) ( )[ ]
( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( )
    
kkH
kkwkkHkukGkHkxkHkkkH
ε
ξ+Γ++++Ψ−Φ+= 111
*
( ) ( ) ( ) ( ) ( ) ( ) ( )kkukGkHkxkHk εζ +++= 1*

100. 101
Estimators
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )111211*1
1
++++++++=+
Γ++Φ=+
kkukGkHkxkHk
kwkkukGkxkkx
εζ
SOLO
Kalman Filter Discrete Case & Colored Measurement Noise
The new discrete dynamic system:
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ) ( ) ( ) ( ){ } ( ){ }
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) lklk
TTT
kRlHlkQkkHlekeE
kEkwEkkHkke
,,11&
1:
δδ
ξε
εε
ε
++ΓΓ+=
+Γ+−=
( ) ( ){ } { }0=lekeE
T
w ξ



=
≠
=
lk
lk
lk
1
0
,δ
Solution (continue – 1)
( ) ( ) ( ) ( ) ( )kkwkkHk ξε +Γ+= 1:
( ) ( ) ( ) ( ) ( )kHkkkHkH Ψ−Φ+= 1:*
( ) ( ){ } ( ) ( ) ( ) ( ) ( )[ ]{ } ( ) ( ) lk
TTTTTTT
kHkkQllHllwkwElkwE ,11 δξε +Γ=++Γ=
To decorrelate measurements and system noises write the discrete dynamic system:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]  
0
1*
1
kkukGkHkxkHkkD
kwkkukGkxkkx
εζ ++−−+
Γ++Φ=+

101. 102
Estimators
( ) ( ) ( ) ( )[ ] ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]kRkHkkQkkHkDkHkkQkkkkDkwkE TTTTT
++ΓΓ+−+ΓΓ==−Γ 1110εε
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) lklk
TTT
kRkRkHkkQkkHlkE ,, *:11 δδεε =++ΓΓ+=
SOLO
Kalman Filter Discrete Case & Colored Measurement Noise
The new discrete dynamic system:
Solution (continue – 2)
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )111211*1
1*1
++++++++=+
−Γ+
+−−++Φ=+
kkukGkHkxkHk
kkDkwk
kukGkHkxkHkkDkukGkxkkx
εζ
ε
ζ
To de-correlate measurement and system noises choose D (k) such that:
( ) ( ){ } ( ) ( ) ( ) ( ) ( )[ ]{ } ( ) ( ) lk
TTTTTTT
kHkkQllHllwkwElkwE ,11 δξε +Γ=++Γ=
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] 1
111
−
++ΓΓ++ΓΓ= kRkHkkQkkHkHkkQkkD TTTT
The Discrete Kalman Filter Estimator is:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( ) ( ){ } 000|0ˆ
1|ˆ*|ˆ|1ˆ
xxEx
kukGkHkkxkHkkDkukGkkxkkkx
==
+−−++Φ=+ ζ
( ) ( ) ( ) ( ) ( )kHkkkHkH Ψ−Φ+= 1:*
The Aprior Covariance Update is:
( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) ( )
( ) 00|0
**|1*|1
PP
kDkRkDkkQkkHkDkkkPkHkDkkkP TTT
=
+ΓΓ+−Φ+−Φ=+

102. 103
Estimators
( ) ( ) ( ) ( )[ ] ( ){ } 0=−Γ kkkDkwkE T
εε
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) lklk
TTT
kRkRkHkkQkkHlkE ,, *:11 δδεε =++ΓΓ+=
SOLO
Kalman Filter Discrete Case & Colored Measurement Noise
The discrete dynamic system:
Solution (continue – 3)
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( ) ( ) ( ) ( )111211*1
1*1
++++++++=+
+−−++Φ=+
kkukGkHkxkHk
kukGkHkxkHkkDkukGkxkkx
εζ
ζ
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] 1
111
−
++ΓΓ++ΓΓ= kRkHkkQkkHkHkkQkkD TTTT
The Discrete Kalman Filter Estimator is:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( ) ( ){ } 000|0ˆ
1/ˆ*|ˆ|1ˆ
xxEx
kukGkHkkxkHkkDkukGkkxkkkx
==
+−−++Φ=+ ζ
( ) ( ) ( ) ( ) ( )kHkkkHkH Ψ−Φ+= 1:*
( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) ( )
( ) 00|0
**|1*|1
PP
kDkRkDkkQkkHkDkkkPkHkDkkkP TTT
=
+ΓΓ+−Φ+−Φ=+
( ) ( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )kRkHkkPkK
kHkRkHkkPkkP
T
T
1
111
**1|11
***|11|1
−
−−−
++=+
++=++
( ) ( ) ( ) ( ) ( ) ( )[ ]kkxkHkkKkkxkkx |1ˆ1*11|1ˆ1|1ˆ ++−++++=++ ζ
Summary:

103. 104
Estimators
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( ) ( ){ } 000|0ˆ
1|ˆ*|ˆ|1ˆ
xxEx
kukGkHkkxkHkkDkukGkkxkkkx
==
+−−++Φ=+ ζ
SOLO
Kalman Filter Discrete Case & Colored Measurement Noise
Solution (continue – 4)
Summary:
( ) ( ) ( ) ( ) ( ) ( )[ ]kkxkHkkKkkxkkx |1ˆ1*11|1ˆ1|1ˆ ++−++++=++ ζ
( ) ( ) ( ) ( )kzkkzk Ψ−+= 1ζ
Table of Content

104. 105
Estimators
( ) ( ) ( ) ( )[ ]∫ −+−=
t
t
dtntHty
0
λλλλ s
SOLO
Optimal State Estimation in Linear Stationary Systems
The output of the Stationary Filter is given by:
Hnxn (t) is the impulse response matrix of the Stationary Filter
( ) ( )[ ] ( ) ( )[ ]{ } ( ) ( ){ } ( ) ( ) ( )tytteteteEtyttytE i
T
i
T
i −==−− yyy :
We want to estimate a vector signal that, after be corrupted by noise ,
passes trough a Linear Stationary Filter. We want to design the filter in order to
estimate the signal using only the measured filter output vector .( )tyn 1×
( )tsn 1× ( )tnn 1×
( )tsn 1×
nnx1 (t) is a noise with autocorrelation
and uncorrelated to the signal
( ) ( ) ( ){ } ( )τττ −=+= tRtntnER nn
T
nn
( ) ( ){ } ( ) ( ){ } { }0=+=+ ττ tstnEtntsE TT
( ) ( ){ } ( ) ( ){ }teteEtraceteteE TT
=
Where the trace of a square matrix A = {ai,j} is the sum of the diagonal terms
{ } ∑=
=× ==
n
i
iinjijinn aatraceAtrace
1
,,,1,, :
( ) ( ) ( )∫ −=
t
t
i dtIty
0
λλλ s
The uncorrupted signal is observed through a linear system, with impulse response
I (t) and output yi (t):
We want to choose a Stationary Filter that minimizes:

105. 106
EstimatorsSOLO
Optimal State Estimation in Linear Stationary Systems (continue – 1)
The Autocorrelation of the error is:
( ) ( ) ( ){ }
( ) ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ] ( )
( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) ( )














−+−−+−−+





−−−−−=










−++−−+










+−−−=
+=
∫∫∫∫
∫∫∫∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
22222221111111
22222221111111
ξξτξξξτξτξξξξξξξξ
ξξτξξξξτξξξξξξξξ
ττ
dtHndtHtIdntHdtHtIE
dtHndtIdntHdtIE
teteER
TTTTT
TTTT
T
ee
ss
ssss
Therefore
( ) ( ) ( )[ ] ( ) ( )[ ]
( )
( ) ( )[ ]
( ) ( ) ( )[ ]
( )
( )∫ ∫
∫ ∫
∞+
∞−
∞+
∞− −
+∞
∞−
+∞
∞− −
−+−+
−+−−+−−−=
212211
21222111
21
21
ξξξτξξξ
ξξξτξτξξξξτ
ξξ
ξξ
ddtHnnEtH
ddtHtIEtHtIR
T
R
T
TT
R
T
ee
nn
  
  
ss
ss

106. 107
Estimators
( ) ( ) ( )[ ] ( ) ( )[ ]
( )
( ) ( )[ ]
( ) ( ) ( )[ ]
( )
( )∫ ∫
∫ ∫
∞+
∞−
∞+
∞− −
+∞
∞−
+∞
∞− −
−+−+
−+−−+−−−=
212211
21222111
21
21
ξξξτξξξ
ξξξτξτξξξξτ
ξξ
ξξ
ddtHnnEtH
ddtHtIEtHtIR
T
R
T
TT
R
T
ee
nn
  
  
ss
ss
( ) ( ) ( )[ ] ( ) ( ) ( )[ ] ( ) ( )sSssssSsssS TTT
−+−−−−= HHHIHI nnssee
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 2)
The Autocorrelation of the error is:
Using the Bilateral Laplace Transform we
obtain:
( ) ( ) ( )
( ) ( )[ ] ( ) ( ) ( )[ ] ( )
( ) ( ) ( )∫ ∫
∫ ∫ ∫
∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
+∞
∞−
−+−−+
−−+−−+−−−−=
−=
212211
21222111 exp
exp
ξξξτξξξ
τξξτξτξτξξξξ
τττ
ddtHRtH
dddstHtIRtHtI
dsRsS
T
nn
TT
eeee
ss
( ) ( )[ ] ( )[ ] ( ) ( )[ ] ( ) ( )[ ] ( )[ ]
( ) ( )
( ) ( )[ ] ( ) ( )[ ] ( ) ( )[ ]
( )
∫ ∫ ∫
∫ ∫ ∫
∞+
∞−
∞+
∞−
−
∞+
∞−
+∞
∞−
+∞
∞−
−−
+∞
∞−
−+−+−−−−−−+
−+−+−−+−−−−−−−−=
222212111
122222121111
expexpexp
expexpexp
ξτξτξτξξξξξξ
ξξτξτξτξτξξξξξξξ
ddsttHsRsttH
dddsttHtIsRsttHtI
s
T
ss
TT
T
TT
  
  
H
nn
H-I
ss

107. 108
Estimators
( ) ( ) ( )[ ] ( ) ( )[ ]
( )
( ) ( )[ ]
( ) ( ) ( )[ ]
( )
( )∫ ∫
∫ ∫
∞+
∞−
∞+
∞− −
+∞
∞−
+∞
∞− −
−+−+
−+−−+−−−=
212211
21222111
21
21
ξξξτξξξ
ξξξτξτξξξξτ
ξξ
ξξ
ddtHnnEtH
ddtHtIEtHtIR
T
R
T
TT
R
T
ee
nn
  
  
ss
ss
( ) ( ) ( )[ ] ( ) ( ) ( )[ ] ( ) ( )sSssssSsssS TTT
−+−−−−= HHHIHI nnssee
SOLO
Optimal State Estimation in Linear Stationary Systems
(continue – 3)
The Autocorrelation of the error is:
Using the Bilateral Laplace Transform we finally
obtained:
where
( ) ( ) ( )
( ) ( )
( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
( )
( ) ( ) ( )
ns
rrrrrrrr
rrrrrrrrrr
rrrr
rrrr
,
expexp
expexpexp
=







=−=−=
−==−−=−=
∫∫
∫∫∫
∞+
∞−
=∞+
∞−
+∞
∞−
−=+∞
∞−
−=+∞
∞−
r
sSdsRdsRsS
sSdsRdsRdsRsS
RR
TT
RR
T
ττττττ
υυυττττττ
τ
τυττ

108. 109
EstimatorsSOLO
Optimal State Estimation in Linear Stationary Systems
(continue – 4)
( )
( ) ( ){ } ( )
( ) ( ){ } ( )
( )0minminmin === τee
tH
T
tH
T
tH
RtraceteteEtraceteteE
( ) ( ) ( ) ( )∫∫
∞+
∞−=
∞+
∞−
===
j
j
ee
j
j
eeee dssS
j
dsssS
j
R
π
τ
π
τ
τ
2
1
exp
2
1
0
0
We want to find the Optimal Stationary Filter, ,that minimizes:( )tHˆ
( )
( ) ( ){ } ( )
( ) ( )
( )
( )
( ) ( )[ ] ( ) ( ) ( )[ ] ( ) ( ){ }∫
∫
∞+
∞−
∞+
∞−
−+−−−=
===
j
j
TTT
s
ee
tH
j
j
ee
tH
T
tH
dssSssssSss
j
trace
RtracedssS
j
traceteteE
HHHIHI nnss
H π
τ
π
2
1
min
0min
2
1
minmin
Using Calculus of Variation we write ( ) ( ) ( ) 0ˆ →Ψ+= εε sss HH
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ] ( ) ( )[ ] ( ) ( )[ ]{ }
( ) ( ) ( ) ( )[ ] ( ){ } ( ) ( )[ ] ( ) ( ) ( ){ } ( ) 0ˆˆ
2
1ˆˆ
2
1
ˆˆˆˆ
2
1
0
=−Ψ+−−+−+−−−−Ψ=
−Ψ+−Ψ++−Ψ−−−−Ψ−−
∂
∂
∫∫
∫
∞+
∞−
∞+
∞−
∞+
∞−
→
j
j
T
j
j
TTT
j
j
TTTTT
dsssSssSss
j
tracedssSsssSs
j
trace
dsssSssssssSsss
j
trace
ε
π
ε
π
εεεε
επ ε
nnssnnss
nnss
HHIHHI
HHHIHI

109. 110
EstimatorsSOLO
Optimal State Estimation in Linear Stationary Systems
(continue – 5)
( ) ( ) ( ) ( )[ ] ( ){ }
( ) ( )[ ] ( ) ( ) ( ){ } ( ) 0ˆˆ
2
1
ˆˆ
2
1
=−Ψ+−−+
−+−−−−Ψ
∫
∫
∞+
∞−
∞+
∞−
j
j
T
j
j
TTT
dsssSssSss
j
trace
dssSsssSs
j
trace
ε
π
ε
π
nnss
nnss
HHI
HHI
Since by tacking –s instead of s in one of the integrals we obtain the other, they are equal
and have zero value:
( ) ( )[ ] ( ) ( ) ( ){ } ( ) 0ˆˆ
2
1
=−Ψ+−−∫
∞+
∞−
j
j
T
dsssSssSss
j
trace ε
π
nnss HHI
This integral is zero for all if and only if:( ) 0≠−Ψ sT
( ) ( )[ ] ( ) ( ) ( ) { }0ˆˆ =+−− sSssSss nnss HHI ( ) ( ) ( )[ ] ( ) ( )sSssSsSs ssnnss IH =+ˆ
Since we can perform a Spectral Decomposition:( ) ( ) ( ) ( )[ ] T
sSsSsSsS −+−=+ nnssnnss
( ) ( ) ( ) ( )sssSsS T
−∆∆=+ nnss
( )s∆ - All poles and zeros are in L.H.P s.
- All poles and zeros are in R.H.P s.( )sT
−∆
( ) ( ) ( ) ( ) ( )sSssss T
ssIH =−∆∆ˆ ( ) ( ) ( ) ( )[ ] ( )sssSss T 1
Part
Realizable
ˆ −−
∆−∆= ssIH

110. 111
Estimators
( ) ( ) ( ) 1&1
1
3
1
3
1
3
2
==
+−
=
−
= sIsS
sss
sS nnss
( ) ( ) ( ) ( )[ ] ( )sssSss T 1
Part
Realizable
ˆ −−
∆−∆= ssIH
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 6)
Example 8.3-2 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.191-192
( ) ( )
( ) ( )

ss T
s
s
s
s
s
s
s
sSsS
−∆∆






−
−






+
+
=
−
−
=+
−
=+
1
2
1
2
1
4
1
1
3
2
2
2nnss
( ) ( ) ( )[ ] ( ) ( )  
Part
realizable-Un
Part
Realizable
2
2
1
1
1
21
3
2
1
1
3
sssss
s
s
ssSs T
−
+
+
=
−+
=
−
−
−
=−∆−
ssI
( )
ss
s
s
s
+
=
+
+
+
=
2
1
2
1
1
1ˆH
Solution:
( )
( ) ( ){ } ( )
( ) ( )[ ] ( ) ( ) ( )[ ] ( ) ( ){ }
( ) ( ) ( ) ( )
1
2
4
2
4
22
4
2
1
ˆˆˆˆ
2
1
2
1
minmin
=
+
=
−
=
−+
=
−+−−−==
∫∫∫
∫∫
∞+
∞−
∞+
∞−
∞+
∞−
RHPLHP
j
j
j
j
TTT
j
j
s
T
tH
ds
s
ds
s
ds
ssj
dssSssssSss
j
tracedsS
j
traceteteE
π
ππ
HHHIHI nnssee
H

111. 112
Estimators
vxy
wBxAx
+=
+=
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 7)
Example 8.5-4 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.211-213
Solution:
( ) ( ){ } ( )
( ) ( ){ } ( )
( ) ( ){ }
( ) ( ){ } 21
21
21
2121
2121
,
0
tt
tvtwE
twtvE
ttRtvtvE
ttQtwtwE
T
T
T
T
∀




==



−=
−=
δ
δ
( ) ( ) ( ) ( ) ( ) 1&& === tItvtntxts
( ) ( ) ( )sWBAsIsS
1−
−= ( ) ( ) ( ) ( ) ( ) TTT
AsIBQBAsIsSsSsS
−−
−−−=−=
1
ss
( ) RsS =nn
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( )[ ]( )
( ) [ ][ ]( ) TT
TTT
TTT
AsIRsRsAsI
AsIAsIRAsIBQBAsI
AsIBQBAsIsssSsS
−−
−−
−−
−−−−−−=
−−−−−+−=
−−−=−∆∆=+
ΤΤ
nnss
2/12/11
1
1
where
RAARRR
ARABQB
TT
TTT
+−=−
+=
2/12/1
ΤΤ
ΤΤ
PRAR
PPPARR TTT
+−=
=−−=
2/1
2/1
&
Τ
Τ
( ) ( ) ( ) ( ) ( )
( ) ( )[ ] ( ) ( )
( ) ( )T
TT
−−=
+−−=−−−=
−−=−−=∆
−
−−−−
−−−
2/11
2/1112/111
2/112/112/11
RsAsI
RRPAsIAsIRRPRAIsAsI
RRRIsAsIRsAsIs

112. 113
Estimators
vxy
wBxAx
+=
+=
( ) ( ) ( ) ( ) ( ) [ ][ ]( ) TTT
AsIRsRsAsIsssSsS
−−
−−−−−−=−∆∆=+ ΤΤnnss
2/12/11
( ) ( ) ( )[ ] ( ) ( )
( )
( ) ( )
( )
( ) ( )  
    
realizableUn
12/1
Realizable
1
12/11
−
−−
−∆
−−−−
−−−=
−−−−−−−=−∆
−
TT
s
TT
sS
TTT
sRBQBAsI
sRAsIAsIBQBAsIssSs
T
T
TI
ss
ss
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 8)
Example 8.5-4 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.211-213
Solution (continue - 1):
( ) ( ){ } ( )
( ) ( ){ } ( )
( ) ( ){ }
( ) ( ){ } 21
21
21
2121
2121
,
0
tt
tvtwE
twtvE
ttRtvtvE
ttQtwtwE
T
T
T
T
∀




==



−=
−=
δ
δ
( ) ( ) ( ) ( ) ( ) 1&& === tItvtntxts
Let decompose the last expression in the Realizable and Un-realizable parts:
( ) ( ) ( ) ( )
TTTT
TTT
ARABQBPRPAPPAARA
PARRPRARRR
+=−−−=
−−==
−
−−
1
12/112/1
ΤΤΤΤ
{ }01
=+−+ −
BQBPRPAPPA T
( ) ( ) ( ) ( )    
realizableUn
12/1
Realizable
1
realizableUn
12/1
Realizable
1
−
−−
−
−−
−−+−=−−− TTT
sRNMAsIsRBQBAsI TT
where M and N must be defined

113. 114
Estimators
vxy
wBxAx
+=
+=
{ }01
=+−+ −
BQBPRPAPPA T
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 9)
Example 8.5-4 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.211-213
Solution (continue - 2):
( ) ( ){ } ( )
( ) ( ){ } ( )
( ) ( ){ }
( ) ( ){ } 21
21
21
2121
2121
,
0
tt
tvtwE
twtvE
ttRtvtvE
ttQtwtwE
T
T
T
T
∀




==



−=
−=
δ
δ
( ) ( ) ( ) ( ) ( ) 1&& === tItvtntxts
Let decompose the last expression in the Realizable and Un-realizable parts:
( ) ( ) ( ) ( )    
realizableUn
12/1
Realizable
1
realizableUn
12/1
Realizable
1
−
−−
−
−−
−−+−=−−− TTT
sRNMAsIsRBQBAsI TT
where M and N must be defined
Pre-multiply this equality by (sI-A) and post-multiply by (-s R1/2
–TT
) to obtain
( ) ( ) NAsIsRMBQB TT
−+−−= T2/1
{ } 2/12/1
0 RMNNRM =⇒=−
2/1
RMAMNAMBQB TTT
−−=−−= TT
PPPARR TTT
=−−= &2/1
Τ
( ) 2/12/12/11
RMAPRARMPRPAPPA TT
−−−−=+−− −−
( ) ( ) ( ) { }012/12/12/1
=−+−−−− −
PRRMPARMPRMPA T 2/1−
= RPM PN =

114. 115
Estimators
vxy
wBxAx
+=
+=
( ) ( ) ( ) ( )[ ] ( ) ( )
( ) ( ) ( )[ ]
( ) ( )
( )
    
sssSs
T
AsIRPAIsRRPAsIsssSss
T 1
Part
Realizable
112/12/111
Part
Realizable
ˆ
−−
∆
−−−
−∆
−−−−
−+−−=∆−∆=
ssI
ssIH
( ) ( ) ( ) ( ) ( )2/12/12/112/11 −−−
+−−=−−=∆ RPRARsAsIRsAsIs Τ
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 10)
Example 8.5-4 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.211-213
Solution (continue - 3):
( ) ( ){ } ( )
( ) ( ){ } ( )
( ) ( ){ }
( ) ( ){ } 21
21
21
2121
2121
,
0
tt
tvtwE
twtvE
ttRtvtvE
ttQtwtwE
T
T
T
T
∀




==



−=
−=
δ
δ
( ) ( ) ( ) ( ) ( ) 1&& === tItvtntxts
Decompose the last expression in the Realizable and Un-realizable parts:
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )      
realizableUn
12/1
Realizable
2/11
realizableUn
12/1
Realizable
1
−
−−−
−
−−−
−−+−=−−−=−∆ TTTT
sRPRPAsIsRBQBAsIssSs TTI ss
PRAR +−=2/1
Τ

115. 116
Estimators
vxy
wBxAx
+=
+=
( ) ( ) ( ) ( )[ ] ( ) ( )
( ) ( ) ( )[ ]
( ) ( )
( )
    
sssSs
T
AsIRPAIsRRPAsIsssSss
T 1
Part
Realizable
112/12/111
Part
Realizable
ˆ
−−
∆
−−−
−∆
−−−−
−+−−=∆−∆=
ssI
ssIH
SOLO
Optimal State Estimation in Linear Stationary Systems (continue – 11)
Example 8.5-4 Sage, “Optimum System Control”, Prentice Hall, 1968, pp.211-213
Solution (continue - 4):
( ) ( ){ } ( )
( ) ( ){ } ( )
( ) ( ){ }
( ) ( ){ } 21
21
21
2121
2121
,
0
tt
tvtwE
twtvE
ttRtvtvE
ttQtwtwE
T
T
T
T
∀




==



−=
−=
δ
δ
( ) ( ) ( ) ( ) ( ) 1&& === tItvtntxts
( ) ( ) ( ) ( )[ ] ( ) ( )[ ]
( ) ( )[ ]( ){ } ( ) ( ) ( )[ ]
( ) ( )[ ]( ){ } ( ) ( )[ ]
( ) ( )[ ]{ } ( ) 111
1
111
111
1
111
1
1111
111111
1111111111ˆ
−−−
−
−−−
−−−
−
−−−
−
−−−−
−−−−−−
−−−−−−−−−−
+−=+−=
+−=−−+=
−+−=−+−=
−+−=+−−−=
RPRPAsIRPAsIRP
IAsIRPAsIAsIRP
AsIRPAsIRPRPAsIIAsI
RPAsIIRPAsIRPAsIAsIRPAsIsH
Finally: ( ) ( ) 111ˆ −−−
+−= RPRPAsIsH
{ }01
=+−+ −
BQBPRPAPPA T
where P is given by:
Continuous Algebraic
Riccati Equation (CARE)
( )xyRPxAx ˆˆˆ 1
−+= −
These solutions are particular solutions of the Kalman Filter algorithm for a
Stationary System and infinite observation time (Wiener Filter) Table of Content

116. 117
Estimators
( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
SOLO
Kalman Filter Continuous Time Case
Assume a continuous time linear dynamic system
( ) vxtHz +=
( ) ( ) ( ){ } ( ) ( ){ } ( )tPteteEtxEtxte
T
xxx =−= &:
( ) ( ) ( ){ } ( ) ( ){ } ( ) ( )21121
0
&: tttQteteEtwEtwte
T
www −=−= δ

( ) ( ) ( ) ( ) ( )∫+=
t
t
dztAtxttBtx
0
,ˆ,ˆ 00 τττ
( ) ( ) ( ){ } ( ) ( ){ } ( ) ( )21121
0
&: tttRteteEtvEtvte
T
vvv −=−= δ

( ) ( ){ } { }021 =teteE
T
wv
Let find a Linear Filter with the state vector that is a function of Z (t) (the history
of z for t0 < τ < t )
( )txˆ
s.t. will minimize
( ) ( )[ ] ( ) ( )[ ]{ } ( ) ( ){ } ( ) ( ) ( )txtxtxwheretxtxEtxtxtxtxEJ TT
−==−−= ˆ:~~~ˆˆ
( ){ } ( ){ }txEtxE =ˆ Unbiased Estimator
( ){ } ( ){ } ( ){ } 0ˆ~ =−= txEtxEtxE

117. 118
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 1)
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( ) ( ) ( ){ } ( )
( ) ( ){ } ( ) ( ) ( ) ( ){ } ( ) ( ){ }txtxEdtxzEtAttBtxtxE
dtAztxEttBtxtxEttBttBtxtxEttB
dtxzEtAdtAztxEddtAzzEtA
txdztAtxttBtxdztAtxttBEtxtxE
T
t
t
TTT
t
t
TTTTT
t
t
T
t
t
TT
t
t
t
t
TT
T
t
t
t
t
T
+−−
−−+
−−=
















−+








−+=
∫
∫
∫∫∫∫
∫∫
0
0
000 0
00
0
00
0
0
0
00
0
000000
0000
ˆ,,ˆ
,ˆ,ˆ,,ˆˆ,
,,,,
,ˆ,,ˆ,~~
τττ
λλλ
ττττττλτλλττ
ττττττ
  
    
( ) ( )[ ] ( ) ( )[ ]{ } ( ) ( ){ } ( ) ( ) ( )txtxtxwheretxtxEtxtxtxtxEJ
TT
−==−−= ˆ:~~~ˆˆ
( ){ } ( ){ } ( ){ } 0ˆ~ =−= txEtxEtxE

118. 119
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 2)
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ){ } ( ) ( ){ } ( ) ( ) ( ) ( ){ }
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( )0000
0000
,ˆˆ,,,
,,
,ˆ,,ˆ,~~
0 0
00
00
ttBtxtxEttBddtAzzEtA
dtxzEtAdtAztxEtxtxE
dztAtxttBtxdztAtxttBtxEtxtxEJ
TT
t
t
t
t
TT
t
t
T
t
t
TTT
T
t
t
t
t
T
++
−−=
















−−








−−==
∫∫
∫∫
∫∫
λτλλττ
ττττττ
ττττττ
Let use Calculus of Variation to find the minimum of J:
( ) ( ) ( ) ( ) ( ) ( )τνετττηεττ ,,ˆ,&,,ˆ, ttBtBttAtA +=+=
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( )
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( ) 0,ˆˆ,ˆ,ˆˆˆ,
,,ˆ,ˆ,
,,
000000000000
0
0 00 0
00
=++
++
−−=
∂
∂
∫∫∫∫
∫∫
=
tttxtxEttBttBtxtxEtt
ddtzzEtAddtAzzEt
dtxzEtdtztxE
J
TTTT
t
t
t
t
TT
t
t
t
t
TT
t
t
T
t
t
TT
νν
λτληλττλτλλττη
τττηττητ
ε
ε
ε

119. 120
( ) ( ){ } ( ) ( ){ } ( ) ( ) ( ){ }
λ
λλττλλ
<<
=−= ∫
tt
dzzEtAztxEztxE
t
t
TTT
0
0,ˆ~
0
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 3)
( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( )
( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( ) 0,ˆˆ,ˆ,,ˆ
,ˆˆ,ˆ,,ˆ
000000
000000
0
0 0
0 0
=








+








−−+
+








−−=
∂
∂
∫ ∫
∫ ∫
=
T
TT
t
t
T
t
t
TT
TT
t
t
T
t
t
TT
tttxtxEttBdtdzzEtAztxE
tttxtxEttBdtdzzEtAztxE
J
νλλητλττλ
νλλητλττλ
ε
ε
ε
This is possible for all η (t,τ), ν (t,t0) iff
( ) 0,ˆ& 0 =ttB
From this we can see that: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )∫−−=−=
t
t
dztAtxttBtxtxtxtx
0
,ˆˆ,ˆˆ~
0
0
0 τττ

Orthogonal Projection Theorem
Wiener-Hopf
Equation
Norbert Wiener
1894 - 1964
Eberhard Frederich Ferdinand
Hopf
1902 - 1983
( ) ( ){ } ( ) ( ) ( ){ } λτλττλ <<= ∫ ttdzzEtAztxE
t
t
TT
0
0
,ˆ

120. 121
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 4)
Solution of Wiener-Hopf Equation ( ) ( ){ } ( ) ( ) ( ){ } λτλττλ <<= ∫ ttdzzEtAztxE
t
t
TT
0
0
,ˆ
Let Differentiate the Wiener-Hopf Equation relative to t:
( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ){ }  
0
λλλλτ TTTTT
ztwEtGztxEtFztwtGtxtFEztx
td
d
EztxE
t
+=+=






=
∂
∂
( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ){ }∫∫ ∂
∂
+=
∂
∂
t
t
TT
t
t
T
dzzEtA
t
ztzEttAdzzEtA
t 00
,ˆ,ˆ,ˆ τλττλτλττ
therefore
( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ){ }∫ ∂
∂
+=
t
t
TTT
dzzEtA
t
ztzEttAztxEtF
0
,ˆ,ˆ τλττλλ
( ) ( ) ( ){ } ( ) ( ) ( ) ( )[ ] ( ){ } ( ) ( ) ( ) ( ){ } ( ) ( ) ( ){ }  
0
,ˆ,ˆ,ˆ,ˆ λλλλ TTTT
ztvEttAztxEtHttAztvtxtHEttAztzEttA +=+=
Now ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }∫=
t
t
TT
dzzEtAtFztxEtF
0
,ˆ τλττλ
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ){ } 0,ˆ,ˆ,ˆ,ˆ
0
=






∂
∂
−−∫
t
t
T
dzzEtA
t
tAtHttAtAtF τλττττ

121. 122
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 5)
Solution of Wiener-Hopf Equation
(continue – 1)
( ) ( ){ } ( ) ( ) ( ){ } λτλττλ <<= ∫ ttdzzEtAztxE
t
t
TT
0
0
,ˆ
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ){ } 0,ˆ,ˆ,ˆ,ˆ
0 0
=






∂
∂
−−∫
≠
t
t
T
dzzEtA
t
tAtHttAtAtF τλττττ
  
( ) ( ) ( ) ( ) ( ) ( ) 0,ˆ,ˆ,ˆ,ˆ =
∂
∂
−− τττ tA
t
tAtHttAtAtFThis is true only if
Define ( ) ( )ttAtK ,ˆ:=
The Optimal Filter was found to be: ( ) ( ) ( )∫=
t
t
dztAtx
0
,ˆˆ τττ
( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ] ( ) ( )
( )
( ) ( ) ( ) ( ) ( ) ( )[ ]txtHtztKtxtFdztAtHtKtFtztK
dztAtHttAtAtFtzttAdztA
t
tzttAtx
td
d
tx
t
t
t
t tKtK
t
t
ˆˆ,ˆ
,ˆ,ˆ,ˆ,ˆ,ˆ,ˆˆ
ˆ
0
00
−+=−+=








−+=
∂
∂
+=
∫
∫∫
  

τττ
τττττττ
Therefore the Optimal Filter is given by: ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]txtHtztKtxtFtx
td
d
ˆˆˆ −+=

122. 123
EstimatorsSOLO
Kalman Filter Continuous Time Case (continue – 6)
Solution of Wiener-Hopf Equation
(continue – 2)
( ) ( ){ } ( ) ( ) ( ){ } λτλττλ <<= ∫ ttdzzEtAztxE
t
t
TT
0
0
,ˆ
( ) ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ){ }∫ ∂
∂
+=
t
t
TTT
dzzEtA
t
ztzEttAztxEtF
0
,ˆ,ˆ τλττλλ
( ) ( ){ } ( ) ( ) ( ) ( )[ ]{ } ( ) ( ){ } ( )λλλλλλ TTTT
HxtxEvxHtxEztxE =+=Now
( ) ( ){ } ( ) ( ) ( )[ ] ( ) ( ) ( )[ ]{ } ( ) ( ) ( ){ } ( ) ( ) ( )
0→<
−+=++=
λ
λδλλλνλλνλ
t
TTTT
ttRHxtxEtHxHttxtHEztzE
( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( )∫+=
t
TTTTT
dGQGttxxEtxtxE
λ
γγλϕγγγγϕλϕγγγϕλ ,,,,
( ) ( ) ( )∫=
t
t
dztAtx
0
,ˆˆ τττ ( ) ( ){ } ( ) ( ) ( ){ } λτλττλ <<= ∫ ttdzzEtAztxE
t
t
TT
0
0
,ˆˆ
Must prove that
( ) ( ) ( ) ( ) ( )tRtHtPttAtK T 1
,ˆ −
==
Table of Content

123. 124
Eberhard Frederich Ferdinand
Hopf
1902 - 1983
In 1930 Hopf received a fellowship from the Rockefeller Foundation to study
classical mechanics with Birkhoff at Harvard in the United States. He arrived
Cambridge, Massachusetts in October of 1930 but his official affiliation was
not the Harvard Mathematics Department but, instead, the Harvard College
Observatory. While in the Harvard College Observatory he worked on many
mathematical and astronomical subjects including topology and ergodic theory.
In particular he studied the theory of measure and invariant integrals in ergodic
theory and his paper On time average theorem in dynamics which appeared in
the Proceedings of the National Academy of Sciences is considered by many as
the first readable paper in modern ergodic theory. Another important contribution
from this period was the Wiener-Hopf equations, which he developed in collaboration
with Norbert Wiener from the Massachusetts Institute of Technology. By 1960, a discrete version of these equations
was being extensively used in electrical engineering and geophysics, their use continuing until the present day. Other
work which he undertook during this period was on stellar atmospheres and on elliptic partial differential equations.
On 14 December 1931, with the help of Norbert Wiener, Hopf joined the Department of Mathematics of the
Massachusetts Institute of Technology accepting the position of Assistant Professor. Initially he had a three years
contract but this was subsequently extended to four years (1931 to 1936). While at MIT, Hopf did much of his
work on ergodic theory which he published in papers such as Complete Transitivity and the Ergodic Principle
(1932), Proof of Gibbs Hypothesis on Statistical Equilibrium (1932) and On Causality, Statistics and Probability
(1934). In this 1934 paper Hopf discussed the method of arbitrary functions as a foundation for probability and
many related concepts. Using these concepts Hopf was able to give a unified presentation of many results in
ergodic theory that he and others had found since 1931. He also published a book Mathematical problems of
radiative equilibrium in 1934 which was reprinted in 1964. In addition of being an outstanding mathematician,
Hopf had the ability to illuminate the most complex subjects for his colleagues and even for non specialists.
Because of this talent many discoveries and demonstrations of other mathematicians became easier to
understand when described by Hopf.
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Hopf_Eberhard.html

124. 125
Estimators
( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
SOLO
Kalman Filter Continuous Time Case (Second Way)
Assume a continuous time dynamic system
( ) vxtHz +=
( ) ( ) ( ){ } ( ) ( ){ } ( )tPteteEtxEtxte
T
xxx =−= &:
( ) ( ) ( ){ } ( ) ( ){ } ( ) ( )21121
0
&: tttQteteEtwEtwte
T
www −=−= δ

( ) ( ) ( ){ } ( ) ( ){ } ( ) ( )21121
0
&: tttRteteEtvEtvte
T
vvv −=−= δ

( ) ( ){ } { }021 =teteE
T
wv
Let find a Linear Filter with the state vector that is a function of Z (t) (the history
of z for t0 < τ < t ). Assume the Linear Filter:
( )txˆ
( ) ( ) ( ) ( ) ( ) ( )tztKtxtKtxtx
td
d
+== ˆ'ˆˆ 
where K’(t) and K (t) will be chosen such that:
1 The Filter is Unbiased: ( ){ } ( ){ }txEtxE =ˆ
2 The Filter will yield a maximum rate of decrease of the error by minimizing
the scalar cost function:
( ) ( )[ ] ( ) ( )[ ]{ } ( )tP
dt
d
tracetxtxtxtxE
dt
d
traceJ
KK
T
KKKK ',',',
minˆˆminmin =−−=

125. 126
Estimators
( ) ( ) ( ) ( ) ( )twtGtxtFtx +=
SOLO
Kalman Filter Continuous Time Case (Second Way – continue - 1)
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]tvtxtHtKtxtKtx ++= ˆ'ˆ
1 The Filter is Unbiased: ( ){ } ( ){ }txEtxE =ˆ
Solution
Define ( ) ( ) ( )txtxtx −= ˆ:~
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )twtGtvtKtxtFtHtKtKtxtKtx −+−++= '~'~
( ){ } ( ){ } ( ){ } 0ˆ~ =−= txEtxEtxE
( ){ } ( ) ( ){ } ( ) ( ) ( ) ( )[ ] ( ){ } ( ) ( ){ } ( ) ( ){ }

0000
'~'~ twEtGtvEtKtxEtFtHtKtKtxEtKtxE −+−++=
We can see that the necessary condition for an unbiased estimator is:
( ) ( ) ( ) ( )tHtKtFtK −='
Therefore: ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )twtGtvtKtxtHtKtFtx −+−= ~~
and the Unbiased Filter has the form:
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]txtHtztKtxtFtx ˆˆˆ −+=

126. 127
EstimatorsSOLO
Kalman Filter Continuous Time Case (Second Way – continue - 2)
Solution
where: ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )twtGtvtKtxtHtKtFtx −+−= ~~
2 The Filter will yield a maximum rate of decrease of the error by minimizing
the scalar cost function:
( ) ( )[ ] ( ) ( )[ ]{ } ( )tP
dt
d
tracetxtxtxtxE
dt
d
traceJ
K
T
KK
minˆˆminmin =−−=
( ) ( ){ } ( ) ( ) ( )[ ] ( ) ( ){ } ( ) ( ) ( )[ ]
( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ } ( )tGtwtwEtGtKtvtvEtK
tHtKtFtxtxEtHtKtFtxtxE
TTTT
TTT
++
−−= ~~~~ 
( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) ( )tGtQtGtKtRtKtHtKtFtPtHtKtFtP TTT
++−−=
To obtain the optimal K (t) that minimize J (t) we perform: ( ) { }0=
∂
∂
=
∂
∂
tPtrace
KK
J 
Using the Matrix Equation: we obtain{ } ( )TT
BBAABAtrace
A
+=
∂
∂
( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) { }022 =+−−=
∂
∂
=
∂
∂
tRtKtHtPtHtKtFtPtrace
KK
J T
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] 1−
+= tRtHtPtHtHtPtFtK TT
Table of Content

127. 128
EstimatorsSOLO
Applications
Table of Content

128. 129
EstimatorsSOLO
Multi-sensor Estimate
Consider a system comprised of two sensors,
each making a single measurement, zi (i=1,2),
of a constant, but unknown quantity, x, in the
presence of random, dependent, unbiased
measurement errors, vi (i=1,2). We want to design an optimal estimator that
combines the two measurements.
{ } { }( ){ }
{ } { }( ){ }
{ }( ) { }( ){ } 11
0
0
1122112
2
2
22222
2
1
2
11111
≤≤−=−−




=−=+=
=−=+=
ρσσρ
σ
σ
vEvvEvE
vEvEvEvxz
vEvEvEvxz
In absence of any other information, we chose an estimator that combines, linearly,
the two measurements:
2211
ˆ zkzkx +=
where k1 and k2 must be found such that:
1. The Estimator is Unbiased: { } { } 0~ˆ ==− xExxE
{ } { } ( ) ( ){ }
{ } { } ( ) { } ( ) 011
~ˆ
2121
0
22
0
11
2211
=−+=−+++=
−+++==−
xkkxEkkvEkvEk
xvxkvxkExExxE
x

121 =+ kk

129. 130
EstimatorsSOLO
Multi-sensor Estimate (continue – 1)
2211
ˆ zkzkx +=
where k1 and k2 must be found such that:
1. The Estimator is Unbiased: { } { } 0~ˆ ==− xExxE 121 =+ kk
2. Minimize the Mean Square Estimation Error: ( ){ } { }2
,
2
,
~minˆmin
2121
xExxE
kkkk
=−
( ){ } ( ) ( )( )[ ]{ } ( )[ ]{ }
{ } ( ) { } ( ) { } ( ) ( )[ ]2111
2
2
2
1
2
1
2
12111
2
2
2
1
2
1
2
1
2
2111
2
2111
2
,
121min121min
1min1minˆmin
1
21
2
2
2
1
1
1121
σσρσσ
σσρσσ
kkkkvvEkkvEkvEk
vkvkExvxkvxkExxE
kk
kkkk
−+−+=










−+−+=
−+=−+−++=−

( ) ( )[ ] ( ) ( ) 0212122121 211
2
21
2
112111
2
2
2
1
2
1
2
1
1
=−+−−=−+−+
∂
∂
σσρσσσσρσσ kkkkkkk
k
21
2
2
2
1
21
2
1
12
21
2
2
2
1
21
2
2
1
2
ˆ1ˆ&
2
ˆ
σσρσσ
σσρσ
σσρσσ
σσρσ
−+
−
=−=
−+
−
= kkk
{ } ( ) 2
2
2
1
21
2
2
2
1
22
2
2
12
,
2
1~min σσ
σσρσσ
ρσσ
≤
−+
−
=xE Reduction of Covarriance Error
Estimator:

130. 131
EstimatorsSOLO
Multi-sensor Estimate (continue – 2)
21
2
1
1
2
2
2
1
1
2
1
1
2
2
11
2
1
1
2
2
2
1
1
2
1
1
2
1
2
21
2
2
2
1
21
2
1
1
21
2
2
2
1
21
2
2
22
22
ˆ
zz
zzx
−−−−
−−−
−−−−
−−−
−+
−
+
−+
−
=
−+
−
+
−+
−
=
σσρσσ
σσρσ
σσρσσ
σσρσ
σσρσσ
σσρσ
σσρσσ
σσρσ
{ } ( ) ( ) 2
2
2
11
2
1
1
2
2
2
1
2
21
2
2
2
1
22
2
2
12
,
2
1
2
1~min σσ
σσρσσ
ρ
σσρσσ
ρσσ
≤
−+
−
=
−+
−
= −−−−
xE
1. Uncorrelated Measurement Noises (ρ =0)
( ) ( ) 2
12
2
2
1
2
21
12
2
2
1
2
1
ˆ zzx
−−−−−−−−
+++= σσσσσσ
{ } 0~min 2
=xE
Fully Correlated Measurement Noises (ρ =±1)
Perfect Sensor (σ 1 = 0)
1
ˆ zx = { } 0~min 2
=xE The estimator will use the perfect sensor as expected.
21
2
1
1
1
2
11
2
1
1
1
1
ˆ zzx −−
−
−−
−
+=
σσ
σ
σσ
σ


131. 132
EstimatorsSOLO
Multi-sensor Estimate (continue – 3)
Consider a system comprised of n sensors,
each making a single measurement, zi (i=1,2,…,n),
of a constant, but unknown quantity, x, in the
presence of random, dependent, unbiased
measurement errors, vi (i=1,2,…,n). We want to design an optimal estimator that
combines the n measurements.
{ } nivEvxz iii ,,2,10 ==+=
or
  
{ } { } { }[ ] { }[ ]{ } RVEVVEVEVE
v
v
v
x
z
z
z
nnnnn
nn
nn
T
V
n
UZ
n
=














=−−=












+












=












2
2211
22
2
22112
112112
2
1
2
1
2
1
0
1
1
1
σσσρσσρ
σσρσσσρ
σσρσσρσ





[ ] ZK
z
z
z
kkkzkzkzkx T
n
nnn =












=+++=

 2
1
212211 ,,,ˆEstimator:

132. 133
EstimatorsSOLO
Multi-sensor Estimate (continue – 4)
ZKx T
=ˆEstimator:
1. The Estimator is Unbiased:
{ } { } { } ( ) { } 01ˆ~
0
=+−=−+=−=

VEKxUKxVKxUKExxExE TTTT
01=−UK T
2. Minimize the Mean Square Estimation Error: { } ( ){ }2
1
2
1
ˆmin~min xxExE
UK
K
UK
K
TT
−=
==
{ } ( )( ){ } { } KRKKVVEKVKVKExE T
UK
K
TT
UK
K
TTT
UK
K
UK
K
TTTT
111
2
1
minminmin~min
====
===
Use Lagrange multiplier λ (to be determined) to include the constraint 01=−UK T
( ) ( )1−−= UKKRKKJ TT
λ ( ) { }0=−=
∂
∂
UKRKJ
K
λ
11
== −
URUUK TT
λ
( ) URURUK T 111 −−−
={ } ( ) 112
1
~min
−−
=
= URUxE T
UK
K
T












=
1
1
1
:

U
URK 1−
= λ
Table of Content

133. 134
SOLO
RADAR Range-Doppler
Target Acceleration Models
Equation of motion of a point mass object are described by:
A
IV
RI
V
R
td
d
x
x
xx
xx











+














=








33
33
3333
3333 0
00
0
A
V
R



- Range vector
- Velocity vector
- Acceleration vector






















=












A
V
R
I
I
A
V
R
td
d
xxx
xxx
xxx






333333
333333
333333
000
00
00
or:
Since the target acceleration vector is not measurable, we assume that it is
a random process defined by one of the following assumptions:
A

1. White Noise Acceleration Model .
3. Piecewise (between samples) Constant White Noise Acceleration Model .
5. Singer Acceleration Model .
2. Wiener Process acceleration model .
4. Piecewise (between samples) Constant Wiener Process Acceleration Model .

134. 135
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 1)
1. White Noise Acceleration Model – Second Order Model

( ) ( ){ } ( ) ( ){ } ( )τδτ −==





+














=








tqwtwEtwEtw
IV
RI
V
R
td
d T
B
x
x
A
xx
xx
x
,0&
0
00
0
33
33
3333
3333






Discrete System ( ) ( ) ( ) ( ) ( )kwkkxkkx Γ+Φ=+1
( ) [ ] 





=+===Φ ∑∫
∞
= 3333
3333
66
00
0!
1
exp:
xx
xx
x
i
ii
T
I
TII
TAITA
i
dAT ττ
2
00
00
00
00
00
0
00
0
00
0
3333
3333
3333
3333
3333
3333
3333
33332
3333
3333
≥∀





=→→





=











=→





= nA
II
A
I
A
xx
xxn
xx
xx
xx
xx
xx
xx
xx
xx

( ) ( ) ( ){ } ( ) ( ) ( )∫ −Φ−Φ=ΓΓ
T
TTT
dTBBTqkkwkwEk
0
τττ ( ) ( ){ } ( )τδτ −= tqwtwE T

135. 136
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 2)
1. White Noise Acceleration Model (continue – 1)
( )
[ ]
( )
τ
τ
τ
d
ITI
I
I
II
TII
q
xx
xx
xx
T
x
x
xx
xx






−










 −
= ∫ 3333
3333
3333
0 33
33
3333
3333 0
0
0
0
( ) ( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( )∫ −Φ−Φ=ΓΓ=ΓΓ
T
TTTTT
dTBBTqkkQkkkwkwEk
0
τττ
( )
( )[ ] ( ) ( )
( )
τ
τ
ττ
ττ
τ
d
ITI
TITI
qdITI
I
TI
q
T
xx
xx
xx
T
x
x
∫∫ 







−
−−
=−




 −
=
0 3333
33
2
33
3333
0 33
33 2/
( ) ( ) ( )








=ΓΓ
TITI
TITI
qkkQk
xx
xxT
33
2
33
2
33
3
33
2/
2/3/
Guideline for Choice of Process Noise Intensity
The change in velocity over a sampling period T are of the order of TqQ =22
For a nearly constant velocity assumed by this model, the choice of q must be such
to give small changes in velocity compared to the actual velocity .V


136. 137
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 3)
2. Wiener Process acceleration model – Third Order Model

( ) ( ){ } ( ) ( ){ } ( )τδτ −==










+






















=












tIqwtwEtwEtw
IA
V
R
I
I
A
V
R
td
d
x
T
B
x
x
x
A
xxx
xxx
xxx
x
33
33
33
33
333333
333333
333333
,0&0
0
000
00
00




  



Discrete System ( ) ( ) ( ) ( ) ( )kwkkxkkx Γ+Φ=+1
( ) [ ]










=++===Φ ∑∫
∞
=
333333
333333
2
333333
22
99
00
00
0
2/
2
1
!
1
exp:
xxx
xxx
xxx
x
i
ii
T
I
TII
TITII
TATAITA
i
dAT ττ
2
000
000
000
000
000
00
000
00
00
333333
333333
333333
333333
333333
333333
2
333333
333333
333333
>∀










=→→










=→










= nA
I
AI
I
A
xxx
xxx
xxx
n
xxx
xxx
xxx
xxx
xxx
xxx

( ) ( ) ( ){ } ( ) ( ) ( )∫ −Φ−Φ=ΓΓ
T
TTT
dTBBTqkkwkwEk
0
τττ
Since the derivative of acceleration is the jerk, this model is also called White Noise Jerk Model.
( ) ( ){ } ( )τδτ −= tIqwtwE x
T
33

137. 138
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 4)
2. Wiener Process Acceleration Model (continue – 1)
( ) ( )
( ) [ ] ( )
( ) ( )
τ
ττ
ττ
ττ
d
ITITI
ITI
I
I
II
TII
TITII
q
xxx
xxx
xxx
xxx
T
x
x
x
xxx
xxx
xxx










−−
−




















−
−−
= ∫
3333
2
33
333333
333333
333333
0
33
33
33
333333
333333
2
333333
2/
0
00
000
0
00
0
2/
( ) ( ) ( ){ } ( ) ( ) ( )∫ −Φ−Φ=ΓΓ
T
TTT
dTBBTqkkwkwEk
0
τττ
( )
( ) ( ) ( )[ ]
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
τ
ττ
τττ
τττ
ττττ
τ
d
ITITI
TITITI
TITITI
qdITITI
I
TI
TI
q
T
xxx
xxx
xxx
xxx
T
x
x
x
∫∫












−−
−−−
−−−
=−−










−
−
=
0
3333
2
33
33
2
33
3
33
2
33
3
33
4
33
3333
2
33
0
33
33
2
33
2/
2/
2/2/4/
2/
2/
( ) ( ) ( )










=ΓΓ
TITITI
TITITI
TITITI
qkkQk
xxx
xxx
xxx
T
33
2
33
3
33
2
33
3
33
4
33
3
33
4
33
5
33
2/6/
2/3/8/
6/8/20/
Guideline for Choice of Process Noise Intensity
The change in acceleration over a sampling period T are of the order of TqQ =33
For a nearly constant acceleration assumed by this model, the choice of q must be such
to give small changes in velocity compared to the actual acceleration .A

( ) ( ){ } ( )τδτ −= tIqwtwE x
T
33

138. 139
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 5)
3. Piecewise (between samples) Constant White Noise Acceleration Model – 2nd
Order

( ) ( ){ } ,0&
0
00
0
33
33
3333
3333
=





+














=








twEtw
IV
RI
V
R
td
d
B
x
x
A
xx
xx
x






Discrete System
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ){ } ( ) ( ) ( ) kl
TTT
lqkllwkwEkkwkkxkkx δΓΓ=ΓΓΓ+Φ=+ 01
( ) [ ] 





=+===Φ ∑∫
∞
= 3333
3333
66
00
0!
1
exp:
xx
xx
x
i
ii
T
I
TII
TAITA
i
dAT ττ
2
00
00
00
00
00
0
00
0
00
0
3333
3333
3333
3333
3333
3333
3333
33332
3333
3333
≥∀





=→→





=











=→





= nA
II
A
I
A
xx
xxn
xx
xx
xx
xx
xx
xx
xx
xx

( ) ( ) ( ) ( )
( )
( )
( ) ( )kw
TI
TI
kw
I
d
I
TII
dkTwBTkwk
x
x
x
x
T
xx
xx
T
kw






=


















 −
=+−Φ=Γ ∫∫ 33
2
33
33
33
0 3333
3333
0
2/0
0
: τ
τ
τττ


139. 140
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 6)
3. Piecewise (between samples) Constant White Noise Acceleration Model
( ) ( ) ( ){ } ( ) ( ) ( ) [ ] klxx
x
x
kl
TTT
TITI
TI
TI
qlqkllwkwEk δδ 33
2
33
33
2
33
00 2/
2/






=ΓΓ=ΓΓ
( ) ( ) ( ){ } ( ) lk
xx
xxTT
TITI
TITI
qllwkwEk ,2
33
3
33
3
33
4
33
0
2/
2/2/
δ








=ΓΓ
Guideline for Choice of Process Noise Intensity
For this model q should be of the order of maximum acceleration magnitude aM.
A practical range is 0.5 aM ≤ q ≤ aM.

140. 141
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 7)
4. Piecewise (between samples) Constant Wiener Process Acceleration Model

( ) ( ){ } 0&0
0
000
00
00
33
33
33
333333
333333
333333
=










+






















=












twEtw
IA
V
R
I
I
A
V
R
td
d
B
x
x
x
A
xxx
xxx
xxx
x




  



Discrete System
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ){ } ( ) ( ) ( ) lk
TTT
lqkllwkwEkkwkkxkkx ,01 δΓΓ=ΓΓΓ+Φ=+
( ) [ ]










=++===Φ ∑∫
∞
=
333333
333333
2
333333
22
99
00
00
0
2/
2
1
!
1
exp:
xxx
xxx
xxx
x
i
ii
T
I
TII
TITII
TATAITA
i
dAT ττ
2
000
000
000
000
000
00
000
00
00
333333
333333
333333
333333
333333
333333
2
333333
333333
333333
≥∀










=→→










=→










= nA
I
AI
I
A
xxx
xxx
xxx
n
xxx
xxx
xxx
xxx
xxx
xxx

( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( ) ( )kw
I
TI
TI
kwd
I
TII
TITII
dkTwBTkwk
x
x
xT
x
x
x
xxx
xxx
xxxT
kw 









=
































−
−−
=+−Φ=Γ ∫∫
33
33
2
33
0
33
33
33
333333
333333
2
333333
0
2/
0
0
0
00
0
2/
: ττ
ττ
τττ


141. 142
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 8)
4. Piecewise (between samples) Constant White Noise acceleration model
( ) ( ) ( ){ } ( ) ( ) ( ) [ ] lkxxx
x
x
x
lk
TTT
ITITI
I
TI
TI
qlqkllwkwEk ,3333
2
33
33
33
2
33
0,0 2/
2/
δδ










=ΓΓ=ΓΓ
( ) ( ) ( ){ } ( ) lk
xxx
xxx
xxx
TT
ITITI
TITITI
TITITI
qllwkwEk ,
3333
2
33
33
2
33
3
33
2
33
3
33
4
33
0
2/
2/
2/2/2/
δ










=ΓΓ
Guideline for Choice of Process Noise Intensity
For this model q should be of the order of maximum acceleration increment over a
sampling period ΔaM.
A practical range is 0.5 ΔaM ≤ q ≤ ΔaM.

142. 143
SOLO
Singer Target Model
R.A. Singer, “Estimating Optimal Tracking Filter Performance for Manned Maneuvering
Target”, IEEE Trans. Aerospace & Electronic Systems”, Vol. AES-6, July 1970,
pp. 437-483
The target acceleration is modeled as a zero-mean random process with exponential
autocorrelation
( ) ( ) ( ){ } T
etataER mTT
ττ
σττ /2 −
=+=
where σm
2
is the variance of the target acceleration and τT is the time constant of its
autocorrelation (“decorrelation time”).
The target acceleration is assumed to:
1. Equal to the maximum acceleration value amax
with probability pM and to – amax
with the same probability.
2. Equal to zero with probability p0.
3. Uniformly distributed between [-amax, amax]
with the remaining probability 1-2 pM – p0 > 0.
( ) ( ) ( )[ ] ( ) ( ) ( )[ ]
max
0
maxmax0maxmax
2
21
0
a
pp
aauaauppaaaaap M
M
−−
−−+++−++= δδδ
RADAR Range-Doppler
Target Acceleration Models (continue – 9)

143. 144
SOLO
Singer Target Model (continue 1)
( ) ( ) ( )[ ] ( ) ( ) ( )[ ]
max
0
maxmax0maxmax
2
21
0
a
pp
aauaauppaaaaap M
M
−−
−−+++−++= δδδ
{ } ( ) ( ) ( )[ ] ( ){ }
( ) ( )[ ]
( ) ( )[ ] 0
22
21
0
2
21
0
max
max
max
max
max
max
max
max
2
max
0
0maxmax
max
0
maxmax
0maxmax
=
−−
+⋅++−=
−−
−−++
+−++==
+
−
−
−−
∫
∫∫
a
a
M
M
a
a
M
a
a
M
a
a
a
a
pp
ppaa
daa
a
pp
aauaau
daappaaaadaapaaE δδδ
{ } ( ) ( ) ( )[ ] ( ){ }
( ) ( )[ ]
( ) ( )[ ]
( )0
2
max
3
max
02
max
2
max
2
max
0
maxmax
2
0maxmax
22
41
3
32
21
2
21
0
max
max
max
max
max
max
max
max
pp
a
a
a
pp
paa
daa
a
pp
aauaau
daappaaaadaapaaE
M
a
a
M
M
a
a
M
a
a
M
a
a
−+=
−−
+−++=
−−
−−++
+−++==
+
−
−
−−
∫
∫∫ δδδ
{ } { } ( )0
2
max
0
222
41
3
pp
a
aEaE Mm −+=−=

σ
Use
( ) ( ) ( )
max0max
00
max
max
aaa
afdaafaa
a
a
+≤≤−
=−∫−
δ
RADAR Range-Doppler
Target Acceleration Models (continue – 10)

144. 145
SOLO
Target Acceleration Approximation by a Markov Process
w (t) x (t)
( )tF
( )tG ∫
x (t)
( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== Given a Continuous Linear System:
Let start with the first order linear system describing Target Acceleration :
( ) ( ) ( )twtata T
T
T +−=
τ
1

( ) ( ) T
T
tt
a ett τ
φ /
0
0
, −−
=
( ) ( ){ }[ ] ( ) ( ){ }[ ]{ } ( )τδττ −=−− tqwEwtwEtwE
( ) ( ){ }[ ] ( ) ( ){ }[ ]{ } ( )ttRtaEtataEtaE TT aaTTTT ,τττ +=−+−+
( ) ( ){ }[ ] ( ) ( ){ }[ ]{ } ( )τττ +=+−+− ttRtaEtataEtaE TT aaTTTT ,
( ) ( ){ }[ ] ( ) ( ){ }[ ]{ } ( ) ( ) 2
, TTTTT aaaaaTTTT ttRtVtaEtataEtaE σ===−−
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )tGtQtGtFtVtVtFtV
td
d TT
xxx ++= ( ) ( ) qtVtV
td
d
TTTT aa
T
aa +−=
τ
2
( ) ( )00 ,
1
, tttt
td
d
TT a
T
a φ
τ
φ −=
where
Target Acceleration Models (continue – 11)
RADAR Range-Doppler

145. 146
SOLO
( ) ( ) qtVtV
td
d
TTTT aa
T
aa +−=
τ
2
( ) ( ) 







−+=
−−
TT
TTTT
t
T
t
aaaa e
q
eVtV ττ τ
22
1
2
0
( )
( ) ( ) ( )
( ) ( ) ( )





<+=+Φ+
>=+Φ
=+
−
−
0,
0,
,
ττττ
ττ
τ
τ
τ
τ
τ
tVetttV
tVetVtt
ttR
TT
T
TTT
TT
T
TTT
TT
aa
T
aaa
aaaaa
aa
( )
( ) ( ) ( )
( ) ( ) ( )





<+=++Φ
>=+Φ
=+
−
−
0,
0,
,
ττττ
ττ
τ
τ
τ
τ
τ
tVetVtt
tVetttV
ttR
TT
T
TTT
TT
T
TTT
TT
aaaaa
aa
T
aaa
aa
For ( ) ( )
2
5 T
statesteadyaaaaaa
T
q
VtVtV TTTTTT
τ
τ
τ
τ
==+≈⇒> −
( ) ( ) ( ) TT
TTTTTTTT
e
q
eVVttRttR
T
T
statesteadyaaaaaaaa
τ
τ
τ
τ
τ
τττ
τ −−
− =≈≈+≈+⇒>
2
,,5
Target Acceleration Approximation by a Markov Process (continue – 1)
Target Acceleration Models (continue – 12)
RADAR Range-Doppler

146. 147
SOLO
( ) 2
0
2
2 T
T
aa qde
q
dVArea T
TT
ττ
τ
ττ τ
τ
=== ∫∫
+∞ −+∞
∞−
τT is the correlation time of the noise w (t) and defines in Vaa (τ) the correlation
time corresponding to σa
2
/e.
One other way to find τT is by tacking the double sides Laplace Transform L2 on τ of:
( ) ( ){ } ( ) qdetqtqs s
ww =−=−=Φ ∫
+∞
∞−
−
ττδτδ τ
τ2L
( ) ( ){ }
( )
( ) ( )sHqsH
s
q
dee
q
Vs
T
T
sT
ssaaaa
T
TTTT
−=
−
=
==Φ ∫
+∞
∞−
−−
−
2
2
/
2
1
2
τ
τ
τ
τ
τ τττ
τL
τT defines the ω1/2 of half of the power spectrum
q/2 and τT =1/ ω1/2.
( ) ( ) ( ) TT
TTTTTTT
e
q
eVttRttR
T
T
aaaaaaa
τ
τ
τ
τ
τ
στττ
τ −−
=≈≈+≈+⇒>
2
,,5
2
T
aT
q
τ
σ 2
2
=
Target Acceleration Approximation by a Markov Process (continue – 2)
RADAR Range-Doppler
Target Acceleration Models (continue – 13)

147. 148
SOLO
Constant Speed Turning Model
RADAR Range-Doppler
Target Acceleration Models (continue – 14)
Denote by and the constant velocity and turning rate vectors.P
td
d
VVV

== 1 ωωω 1=

VVVV
td
d
VVV
td
d
V
td
d
A



×=×=+





== ωω 111:
0
( ) ( ) VVVVV
td
d
V
td
d
A
td
d 





22
0:
0
ωωωωωωωω −=−⋅=××=×+×





=
=
Define
( ) ( )
2
00
:
V
AV

 ×
=ω
Denote the position vector of the vehicle relative to an Inertial system..P

Therefore A
IA
V
P
I
I
A
V
P
td
d 



  













+
























−
=












Λ
0
0
00
00
00
2
ω
We want to find ф (t) such that ( ) ( ) ( )TTT ΦΛ=Φ
Continuous Time
Constant Speed
Target Model

148. 149
SOLO
Constant Speed Turning Model (continuous – 1)
RADAR Range-Doppler
Target Acceleration Models (continue – 15)
A
B
C
O
θ
φφ
nˆ
v

1v

Let rotate the vector around by a large angle
, to obtain the new vector
→
= OAPT

nˆ
Tωθ =
→
=OBP

From the drawing we have:
→→→→
++== CBACOAOBP

TPOA

=
→
( )( )θcos1ˆˆ −××=
→
TPnnAC
 Since direction of is: ( ) ( ) φsinˆˆ&ˆˆ TTT PPnnPnn

=××××
and it’s length is:
AC
→
( )θφ cos1sin −TP

( ) θsinˆ TPnCB

×=
→
Since has the direction and the
absolute value
CB
→
TPn

׈
θφsinsinv
( )( ) ( ) θθ sinˆcos1ˆˆ TTT PnPnnPP

×+−××+=
( ) ( )[ ] ( ) ( )TPnTPnnPP TTT ωω sinˆcos1ˆˆ

×+−××+=
We will find ф (T) by direct computation of a rotation:

149. 150
SOLO
Constant Speed Turning Model (continuous – 2)
RADAR Range-Doppler
Target Acceleration Models (continue – 16)
( ) ( ) ( ) ( )TPnnTPn
Td
Pd
V TT ωωωω



sinˆˆcosˆ ××+×==
( ) ( )TT PnTVV

×=== ˆ0 ω
( ) ( ) ( ) ( )TPnnTPn
Td
Vd
A TT ωωωω cosˆˆsinˆ 22



××+×−==
( ) ( )TT PnnTAA

××=== ˆˆ0 2
ω
( ) ( )[ ]
( ) ( )
( ) ( )





+−=
+=
−++=
−
−−
TT
TT
TTT
ATVTA
ATVTV
ATVTPP



ωωω
ωωω
ωωωω
cossin
sincos
cos1sin
1
21
( ) ( ) ( ) ( )[ ]TPnnTPnPP TTT ωω cos1ˆˆsinˆ −××+×+=


150. 151
SOLO
Constant Speed Tourning Model (continuous – 3)
RADAR Range-Doppler
Target Acceleration Models (continue – 17)
( ) ( )[ ]
( ) ( )
( ) ( )





+−=
+=
−++=
−
−−
TT
TT
TTT
ATVTA
ATVTV
ATVTPP



ωωω
ωωω
ωωωω
cossin
sincos
cos1sin
1
21
( ) ( )[ ]
( ) ( )
( ) ( )
( )






















−
−
=












Φ
−
−−
T
T
T
T
A
V
P
TT
TT
TTI
A
V
P



  



ωωω
ωωω
ωωωω
cossin0
sincos0
cos1sin
1
21
Discrete Time
Constant Speed
Target Model

151. 152
SOLO
Constant Speed Tourning Model (continuous – 4)
RADAR Range-Doppler
Target Acceleration Models (continue – 18)
( )
( ) ( )[ ]
( ) ( )
( ) ( ) 









−
−
=Φ −
−−
TT
TT
TTI
T
ωωω
ωωω
ωωωω
cossin0
sincos0
cos1sin
1
21
( )
( ) ( )[ ]
( ) ( )
( ) ( ) 









−
−−
=Φ −
−−
−
TT
TT
TTI
T
ωωω
ωωω
ωωωω
cossin0
sincos0
cos1sin
1
21
1
( )
( ) ( )
( ) ( )
( ) ( ) 









−−
−=Φ
−
TT
TT
TT
T
ωωωω
ωωω
ωωω
sincos0
cossin0
sincos0
2
1

We want to find Λ (t) such that
( ) ( ) ( )TTT ΦΛ=Φ therefore ( ) ( ) ( )TTT 1−
ΦΦ=Λ 
( ) ( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )[ ]
( ) ( )
( ) ( ) 









−
−−










−−
−=ΦΦ=Λ −
−−−
−
TT
TT
TTI
TT
TT
TT
TTT
ωωω
ωωω
ωωωω
ωωωω
ωωω
ωωω
cossin0
sincos0
cos1sin
sincos0
cossin0
sincos0
1
21
2
1
1










−
=
00
100
010
2
ω
We recovered the transfer matrix for the continuous
case.

152. 153
SOLO
Force Equations
( )g
1 
mTF
m
A A ++=
Lzgg 1=
where
Fixed Wing Air Vehicle Acceleration Model
RADAR Range-Doppler
Target Acceleration Models (continue – 19)
( ) ( ) WWA zLxDF 11 αα −−=
 -Drag and Lift Aerodynamic Forces as functions
of angle of attack α
BxTT 1=

- Thrust Force
For small angle of attack α the wind (W) coordinates and body (B) coordinates
coincide, therefore we will use only wind (W) and Local Level Local North (L)
coordinates, related by:
W
LC - Transformation Matrix from (L) to (W)
- earth gravitation
( )
LWW zgz
m
L
x
m
DT
A 111 +−
−
≈

Force Equations
By measuring Air Vehicle trajectory we can estimate its, position, velocity and acceleration
vectors, , CL
W
matrix and (T – D)/m and L / m.( )AVP

,,
WxVV 1=

- Air Vehicle Velocity Vector

153. 154
SOLO
Fixed Wing Air Vehicle Acceleration Model (continue – 1)
RADAR Range-Doppler
Target Acceleration Models (continue – 20)
( ) WWWWWWWWWWWWW
L
W
W
L
zVqyVrxVxzryqxpVxV
td
xd
VxV
td
Vd
11111111
1
1 −+=×+++=+= 

( )
( ) ( )
( )
( ) 











+−
+
+
=










+










−
−
=










−
=










=








=
gCl
gC
gCf
gC
L
DT
m
Vq
Vr
V
A
A
A
td
Vd
A
W
L
W
L
W
L
W
L
W
W
zW
yW
xWW
L
W
3,3
3,20
3,1
1
0
0
0
1


( )[ ]
( ) VgCr
VgClq
W
LW
W
LW
/3,2
/3,3
=
−=
Therefore the Air vehicle Acceleration in it’s Wind (W) Coordinates is given by:
( ) ( )WWWWWWWWWWWWWW
I
xqyplyrzqfzlxfzlxfzlxf
td
Ad
A 1111111111: +−−+−+−=−+−==
⋅⋅



( ) ( )
( ) gCAmLl
gCAmDTf
W
LzW
W
LxW
3,3/:
3,1/:
+−==
−=−=
( )










−−
+
−
=
W
WW
W
W
qfl
rfpl
qlf
A




154. 155
SOLO
Fixed Wing Air Vehicle Acceleration Model (continue – 2)
RADAR Range-Doppler
Target Acceleration Models (continue – 21)
( )[ ]
( ) VgCr
VgClq
W
LW
W
LW
/3,2
/3,3
=
−=
We found:
( )
mLl
mDTf
/:
/:
=
−=
( )










−−
+
−
=
W
WW
W
W
qfl
rfpl
qlf
A


 , pW are pilot controlled and are modeled as zero mean
random variables
lf ,
( )
{ }
( )[ ]
( )[ ] ( )
( )[ ] ( )[ ] 











−−−
−
−−
=










−
−
=
VgClgCV
VgCgCV
VgCll
qf
rf
ql
AE
W
L
W
L
W
L
W
L
W
L
W
W
W
W
/3,31,3
/2,31,3
/3,3

 ( )
{ } ( )
( )[ ]
( )[ ] ( )
( )[ ] ( )[ ]











−−−
−
−−
=
gClgCV
gCgCV
gCll
C
V
AE
W
L
W
L
W
L
W
L
W
L
TW
L
L
3,31,3
2,31,3
3,3
1


( ) ( )
{ } ( )










−
=−
l
pl
f
CAEA W
TW
L
LL



( ) ( )
{ } ( ) ( )
{ } ( ) W
L
l
p
f
TW
L
T
LLLL
ClCAEAAEAE W












=









 −



 −
2
22
2
00
00
00



σ
σ
σ

155. 156
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 22)

( )tA
IA
V
R
I
I
A
V
R
td
d
B
x
x
x
A
xxx
xxx
xxx
x





  













+






















=












33
33
33
333333
333333
333333
0
0
000
00
00
Discrete System
( ) ( ) ( ) ( ) ( )kAkkxkkx

Γ+Φ=+1
( ) [ ]










=++===Φ ∑∫
∞
=
333333
333333
2
333333
22
99
00
00
0
2/
2
1
!
1
exp:
xxx
xxx
xxx
x
i
ii
T
I
TII
TITII
TATAITA
i
dAT ττ
2
000
000
000
000
000
00
000
00
00
333333
333333
333333
333333
333333
333333
2
333333
333333
333333
≥∀










=→→










=→










= nA
I
AI
I
A
xxx
xxx
xxx
n
xxx
xxx
xxx
xxx
xxx
xxx

( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( ) ( )kA
TI
TI
TI
kAd
II
TII
TITII
dkTABTkAk
x
x
xT
x
x
x
xxx
xxx
xxxT
kA














=
































−
−−
=+−Φ=Γ ∫∫
33
33
3
33
0
33
33
33
333333
333333
2
333333
0
2/
6/
0
0
00
0
2/
: ττ
ττ
τττ
Fixed Wing Air Vehicle Acceleration Model (continue – 3)

156. 157
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 23)
( )

( ) ( )
( )
( )L
B
x
x
x
kx
L
A
xxx
xxx
xxx
L
kx
A
TI
TI
TI
A
V
R
I
TII
TITII
A
V
R





  













+






















=












+
33
2
33
3
33
333333
333333
2
333333
1
4/
6/
00
0
2/
Discrete System
Fixed Wing Air Vehicle Acceleration Model (continue – 4)
( ) ( )
{ } ( )










−
=−
l
pl
f
CAEA W
TW
L
LL



( ) ( )
{ } ( ) ( )
{ } ( ) W
L
l
p
f
TW
L
T
LLLL
ClCAEAAEAE W












=









 −



 −
2
22
2
00
00
00



σ
σ
σ

157. 158
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 24)
Fixed Wing Air Vehicle Acceleration Model (continue – 5)
We need to defined the matrix CL
W
.
For this we see that is along and is alongWx1 Wz1V

L

( )
( ) ( )
( )
( )
( )
( )











=










==
3,1
2,1
1,1
0
0
1
11
W
L
W
L
W
L
TW
L
W
W
TW
L
L
W
C
C
C
CxCx
( )
( ) ( )
( )
( )
( )
( )











=










==
3,3
2,3
1,3
1
0
0
11
W
L
W
L
W
L
TW
L
W
W
TW
L
L
W
C
C
C
CzCz
Therefore ( ) ( ) ( ) ( )
( ) ( )
[ ]LLVLVLVVC LLLLTW
L ///





×=
LWW zgzlxfA 111 +−=

Azgxfzl LWW

−+= 111
( ) ( ) ( ) ( )[ ] ( ) ( ) gCVgCACACACgCAf
W
L
W
L
V
z
W
Ly
W
Lx
W
L
W
LxW 3,13,13,12,11,13,1 −=−++=−= 
  

( )
( ) ( ) ( )[ ] ( )
( )
( )
( ) 









−










+




















−++=
z
y
x
W
L
W
L
W
L
W
L
V
z
W
Ly
W
Lx
W
L
L
W
A
A
A
g
C
C
C
gCACACACzl
1
0
0
3,1
2,1
1,1
3,13,12,11,11
  

( ) ( ) ( )[ ] [ ] 222
/3,12,11,1 zyxzyx
W
L
W
L
W
L VVVVVVCCC ++= 
( ) ( ) ( )[ ] [ ] VAVAVAVACACACAV zzyyxxz
W
Ly
W
Lx
W
LzW /3,12,11,1 ++=++==

158. 159
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 25)
Fixed Wing Air Vehicle Acceleration Model (continue – 6)
CL
W,
f, l , qW, rW Computation from Vectors
( ) ( )LL
AV

,
Compute:
( ) ( ) ( )[ ] [ ] 222
/3,12,11,1 zyxzyx
W
L
W
L
W
L VVVVVVCCC ++= 1
( ) ( ) ( )[ ] [ ] VAVAVAVACACACAV zzyyxxz
W
Ly
W
Lx
W
LzW /3,12,11,1 ++=++==2
( ) ( )
( )
( )
( )
( )
( )
( )
Abs
AgVVVgVV
AVVVgVV
AVVVgVV
C
C
C
z
L
L
zzz
yyz
xxz
W
L
W
L
W
L
L
W
L
/
//
//
//
3,3
2,3
1,3
1










−+−
−−
−−
=












==



3
( )[ ] ( )[ ] ( )[ ]222
//////: zzzyyzxxz AgVVVgVVAVVVgVVAVVVgVVAbs −+−+−−+−−= 
( ) ( ) ( ) ( )
( ) ( )
[ ]LLVLVLVVC LLLLTW
L ///





×=4
( )
( ) ( )
( )
( )












×=
LL
VLVL
VV
C
L
LL
L
W
L
/
/
/



or
( )[ ]
( ) VgCr
VgClq
W
LW
W
LW
/3,2
/3,3
=
−=( )
( ) ( ) ( )[ ] ( ) gCACACACl
gCVf
W
Lz
W
Ly
W
Lx
W
L
W
L
3,33,32,31,3
3,1
+++−=
−= 
5

159. 160
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 26)
Ballistic Missile Acceleration Model
( )g
1 
mTF
m
A A ++=
( ) ( )
( ) ( ) ( )[ ]WLWDref
WWA
zVCxVCS
VZ
zVLxVDF
1,1,
2
1,1,
2
αα
ρ
αα
−−=
−−=
 - Drag and Lift Aerodynamic Forces as
functions of angle of attack α and
air pressure ρ (Z)
BxTT 1=

- Thrust Force
For small angle of attack α the wind (W) coordinates and body (B) coordinates
coincide, therefore we will use only wind (W) and Local Level Local North (L)
coordinates, related by:
W
LC - Transformation Matrix from (L) to (W)
L
T
L z
R
zgg 11 2
µ
==
where - earth gravitation
( )
LWW zgz
m
L
x
m
DT
A 111 +−
−
≈

Force Equations
WxVV 1=

- Air Vehicle Velocity Vector
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

160. 161
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 27)
Ballistic Missile Acceleration Model (continue – 1)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr
( )
( )
2
0
0
0
0
0
1
0
0
sin
cos
1 0
0
0
T
W
L
W
W
zW
yW
xWW
L
W
R
C
L
L
DT
m
Vq
Vr
V
A
A
A
td
Vd
A
µ
ϕ
ϕ










+










−
−
−
=










−
=










=








=


Therefore the Air vehicle Acceleration in it’s Wind0 (W0 – for which φ =0 ) Coordinates is
given by:
( ) WWWWWWWWWWWWW
L
W
W
L
zVqyVrxVxzryqxpVxV
td
xd
VxV
td
Vd
11111111
1
1 −+=×+++=+= 

Define:
m
T
t =: ( )
m
CS
dd
VZ
m
D Dref
CC == :&
2
:
2
ρ
( ) ( ) ( ) ( )tzzt
m
CS
zz
VZ
t
m
L
CC
Lref
CC ωωω
ρ
ω sin:&cos:&
2
:cos
2
−=== 
We assume that the ballistic missile performs a barrel-roll motion with constant
rotation rate ω. Therefore at each instant the aerodynamic lift force will be at an
angle φ = ω t.
Assuming constant CL/m: (barrel-roll model)02
=+ CC zz ω
Assuming constant ω (barrel-roll model)0=ω

161. 162
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 28)
Ballistic Missile Acceleration Model (continue – 2)
CL
W0
Computation:
( ) 2/1222
ZYXV  ++=( )










=
Z
Y
X
V L




Define: ψ - trajectory azimuth angle ( )XY ,tan 1−
=ψ
γ - trajectory pitch angle ( )221
,tan YXZ  += −
γ
[ ] [ ]










−
−
=










−









 −
==
γψγψγ
ψψ
γψγψγ
ψψ
ψψ
γγ
γγ
ψγ
cossinsincossin
0cossin
sinsincoscoscos
100
0cossin
0sincos
cos0sin
010
sin0cos
32
0W
LC

162. 163
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 29)
Ballistic Missile Acceleration Model (continue – 3)
( )
( )
( ) ( )2
2
2
2
1
0
0
2
1
2
1
2
1
0
ZR
z
V
zV
dVt
C
Z
Y
X
td
Vd
A
c
C
C
C
TW
L
L
L
L
+










+


















+
−
−
=










=








=
µ
ω
ρ
ρ
ρ





where:
Assuming constant CL/m (barrel-roll model)02
=+ CC zz ω
0=Cd Assuming constant CD/m
( ) 2/1222
ZYXV  ++=
Assuming constant ω (barrel-roll model)0=ω

163. 164
SOLO
RADAR Range-Doppler
Target Acceleration Models (continue – 30)
Ballistic Missile Acceleration Model (continue – 4)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( )
( )
( )
( )




































+
+
+








































































−
−−
−−
−−
=
































0
0
0
0
3,1
2,1
1,1
0
0
0
0000000000
0000000000
000000000
0000000000
0
2
1
3,1
2
1
3,3
2
1
3,2000000
0
2
1
2,1
2
1
2,3
2
1
2,2000000
0
2
1
1,1
2
1
1,3
2
1
1,2000000
0000100000
0000010000
0000001000
2
2
222
222
222
ZR
tC
tC
tC
d
z
z
Z
Y
X
Z
Y
X
VCVCVC
VCVCVC
VCVCVC
d
z
z
Z
Y
X
Z
Y
X
td
d
C
W
L
W
L
W
L
C
C
C
W
L
W
L
W
L
W
L
W
L
W
L
W
L
W
L
W
L
C
C
C
µ
ω
ω
ρρ
ω
ρ
ρρ
ω
ρ
ρρ
ω
ρ
ω








System Dynamics is given by:

164. 165
SOLO
Target Acceleration Models (continue – 31)
Ballistic Missile Acceleration Model (continue – 5)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

165. 166
SOLO
Target Acceleration Models (continue – 32)
Ballistic Missile Acceleration Model (continue – 6)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

166. 167
SOLO
Target Acceleration Models (continue – 33)
Ballistic Missile Acceleration Model (continue – 7)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

167. 168
SOLO
Target Acceleration Models (continue – 34)
Ballistic Missile Acceleration Model (continue – 8)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

168. 169
SOLO
Target Acceleration Models (continue – 35)
Ballistic Missile Acceleration Model (continue – 9)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr

169. 170
SOLO
Target Acceleration Models (continue – 36)
Ballistic Missile Acceleration Model (continue – 10)
MV
Bx
By
Bz
Wz
Wy
Wx
α
β
α
β
Bp
Wp
Bq
WqBr
Wr
Table of Content

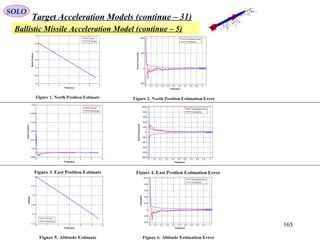
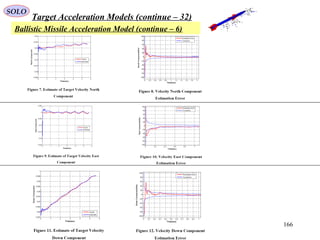
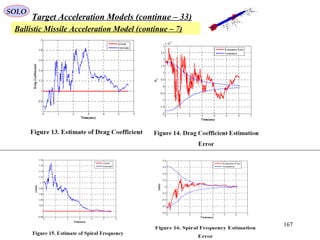
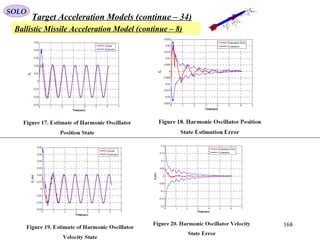
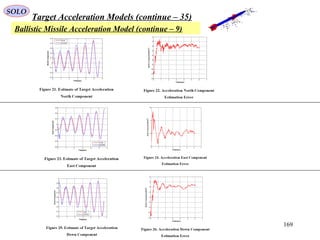
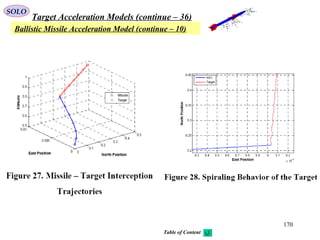
170. 171171
EstimatorsSOLO
Kalman Filter for Filtering Position and Velocity Measurements
Assume a Cartezian Model of a Non-maneuvering Target:

w
x
x
x
x
td
d
wx
xx
BA






+











=





⇒



=
=
1
0
00
10




( ) [ ] 





=+=+++++==Φ ∫ 10
1
!
1
2
1
exp: 22
0
T
TAITA
n
TATAIdAT nn
T
ττ
2
00
00
00
00
00
10
00
10
00
10 2
≥∀





=→→





=











=→





= nAAA n







+





=+=
2
1
v
v
x
x
vxz
 Measurements
( ) ( ) ( )






=




 −−
=










 −
=−Φ=Γ ∫∫ T
TT
d
T
dBTT
T
TT
2/2/
1
0
10
1
:
2
0
2
00 τ
τ
τ
τ
ττ
Discrete System



+=
Γ+Φ=
++++
+
1111
1
kkkk
kkkkk
vxHz
wxx
{ }
{ }


















==+





=
==





+





=
++++++
ΓΦ
+
+
kj
V
PT
jkkkk
H
k
kjq
T
jkkkkk
vvERvxz
wwEQw
T
T
x
T
x
k
kk
δ
σ
σ
δσ
2
2
111111
2
2
1
0
0
&
10
01
&
2/
10
1
1



171. 172172
EstimatorsSOLO
Kalman Filter for Filtering Position and Velocity Measurements (continue – 1)
The Kalman Filter:
( )



−+=
Φ=
+++++++
+
kkkkkkkkk
kkkkk
xHzKxx
xx
|1111|11|1
||1
ˆˆˆ
ˆˆ
T
kkk
T
kkkkkk QPP ΓΓ+ΦΦ=+ ||1
[ ]TT
T
T
Tpp
ppT
pp
pp
P q
kkkk
kk 2/
2/
1
01
10
1 22
2
|2212
1211
|12212
1211
|1 σ





+

















=





=
+
+
[ ]TT
T
T
Tpp
TppTpp
pp
pp
P q
kkkk
kk 2/
2/
1
01 22
2
|2212
22121211
|12212
1211
|1 σ





+










 ++
=





=
+
+
( ) ( )
( ) kkqq
qq
q
kkkk
kk
TpTTpp
TTppTTpTpp
TT
TT
pTpp
TppTpTpp
pp
pp
P
|
22
22
23
2212
23
2212
242
221211
2
23
34
|222212
2212
2
221211
|12212
1211
|1
2/
2/4/2
2/
2/4/2








+++
+++++
=








+





+
+++
=





=
+
+
σσ
σσ
σ

172. 173173
EstimatorsSOLO
Kalman Filter for Filtering Position and Velocity Measurements (continue – 2)
The Kalman Filter:
( )



−+=
Φ=
+++++++
+
kkkkkkkkk
kkkkk
xHzKxx
xx
|1111|11|1
||1
ˆˆˆ
ˆˆ
[ ] 1
11|111|11
−
+++++++ += k
T
kkkk
T
kkkk RHPHHPK
( )( ) kkP
V
VP
kk
V
P
pp
pp
ppppp
pp
pp
pp
pp
pp
|1
2
1112
12
2
22
2
12
2
22
2
112212
1211
|1
1
2
2212
12
2
11
2212
1211 1
++
−
















+−
−+
−++






=
















+
+






=
σ
σ
σσσ
σ
( )( )
( )
( ) kkPV
PV
VP pppppppp
pppppppp
ppp
/1
2
12
2
11222212
2
122212
2
1212111211
2
12
2
2211
2
12
2
22
2
11
1
+
















−+−+
++−−+
−++
=
σσ
σσ
σσ
( )( )
( )
( ) kkPV
PV
VP pppp
pppp
ppp
|1
2
12
2
1122
2
12
2
12
2
12
2
2211
2
12
2
22
2
11
1
+
















−+
−+
−++
=
σσ
σσ
σσ

173. 174174
EstimatorsSOLO
Kalman Filter for Filtering Position and Velocity Measurements (continue – 2)
The Kalman Filter:
[ ] 1
11/111/11
−
+++++++ += k
T
kkkk
T
kkkk RHPHHPK
( )( )
( )
( ) kkPV
PV
VP pppp
pppp
ppp
/1
2
12
2
1122
2
12
2
12
2
12
2
2211
2
12
2
22
2
11
1
+
















−+
−+
−++
=
σσ
σσ
σσ
2
23
34
/222212
2212
2
221211
/12212
1211
/1
2/
2/4/2
q
kkkk
kk
TT
TT
pTpp
TppTpTpp
pp
pp
P σ








+





+
+++
=





=
+
+
( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( ) 4///2//1
2////1
//1
422
22121111
32
221212
22
2222
TTkkpTkkpkkpkkp
TTkkpkkpkkp
Tkkpkkp
q
q
q
σ
σ
σ
+++=+
++=+
+=+

174. 175175
EstimatorsSOLO
Kalman Filter for Filtering Position and Velocity Measurements (continue – 3)
The Kalman Filter:
[ ] 1
11/111/11
−
+++++++ += k
T
kkkk
T
kkkk RHPHHPK
( )
( ) ( )
( ) ( ) ( )



+−−−
−−
=+
++++++++
+++
+ T
kkk
T
kkkkk
kkk
k
KRKHKIPHKI
PHKI
P
11111111
111
1
( )( )
( )
kkPV
PV
VPk
k
ppppp
pppp
pppKK
KK
K
/1
2
222211
2
12
2
12
2
12
2
12
2
2211
2
12
2
22
2
1112221
1211
1
1
++
+
















++−
−+
−++
=





=
σσ
σσ
σσ
( )( )
( )
( ) kkVPV
PPV
VP
kk
pp
pp
ppp
HKI
/1
22
11
2
12
2
12
22
22
2
12
2
22
2
11
11
1
+
++
















+−
−+
−++
=−
σσσ
σσσ
σσ
( )
( )( )
( )
( ) kkVPV
PPV
VP
kkkkkk
pp
pp
pp
pp
ppp
PHKIP
/1
2212
1211
22
11
2
12
2
12
22
22
2
12
2
22
2
11
/1111/1
1
+
+++++






















+−
−+
−++
=−=
σσσ
σσσ
σσ
( )( )
( )[ ]
( )[ ]














=








=
















−+
−+
−++
=
+
++
++
2
2
12221
1211
1
2
22
2
21
2
12
2
11
/1
2
1222
2
11
222
12
22
12
2
1211
2
22
2
2
12
2
22
2
11
1/1
0
0
1
V
P
k
kVP
VP
kkPVVP
VPVP
VP
kk
KK
KK
KK
KK
pppp
pppp
ppp
P
σ
σ
σσ
σσ
σσσσ
σσσσ
σσ

175. 176
Estimators

w
x
x
x
x
td
d
BA






+











=





1
0
00
10



SOLO
We want to find the steady-state form of the filter for
Assume that only the position measurements are available
x
x

- position
- velocity
[ ] { } { } kjjkkk
k
kkkk RvvEvEv
x
x
vxHz δ==+





=+= ++++
+
++++ 1111
1
1111 0&01

Discrete System



+=
Γ+Φ=
++++
+
1111
1
kkkk
kkkkk
vxHz
wxx
{ }
[ ] { }








==+=
==





+





=
++++++
ΓΦ
+
+
kjP
T
jkkkk
H
k
kjw
T
jkkkkk
vvERvxz
wwEQw
T
T
x
T
x
k
kk
δσ
δσ
2
111111
2
2
1
&01
&
2/
10
1
1


α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model

176. 177
EstimatorsSOLO
Discrete System



+=
Γ+Φ=
++++
+
1111
1
kkkk
kkkkk
vxHz
wxx
{ }
[ ] { }








==+=
==





+





=
++++++
ΓΦ
+
+
kjP
T
jkkkk
H
k
kjw
T
jkkkkk
vvERvxz
wwEQw
T
T
x
T
x
k
kk
δσ
δσ
2
111111
2
2
1
&01
&
2/
10
1
1


( ) ( ) ( ) ( ) ( )11/111 +++++=+ kRkHkkPkHkS
T
( ) ( ) ( ) ( ) 1
11/11
−
+++=+ kSkHkkPkK T
When the Kalman Filter reaches the steady-state
( ) ( ) 





=++=
∞→∞→
2212
1211
1/1lim/lim
pp
pp
kkPkkP
kk
( ) 





=+
∞→
2212
1211
/1lim
mm
mm
kkP
k
[ ] 2
11
2
1212
1211
0
1
01 PP m
mm
mm
S σσ +=+











=
( )
( )







+
+
=
+












=





= 2
1112
2
1111
2
112212
1211
12
11
/
/1
0
1
P
P
P mm
mm
mmm
mm
k
k
K
σ
σ
σ
( ) ( ) ( )[ ] ( )kkPkHkKIkkP /1111/1 +++−=++[ ] 



















−





=





2212
1211
12
11
2212
1211
01
10
01
mm
mm
k
k
pp
pp
( ) ( )
( )
( ) ( )
( ) ( )







+−+
++
=





−−
−−
= 2
11
2
1222
2
1112
2
2
1112
22
1111
2
1212221211
12111111
//
//
1
11
PPP
PPPP
mmmmm
mmmm
mkmmk
mkmk
σσσ
σσσσ
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 1)

177. 178
EstimatorsSOLO
From ( ) ( ) ( ) ( ) ( )kQkkkPkkkP
T
+ΦΦ=+ //1
we obtain ( ) ( ) ( ) ( )[ ] ( )kkQkkPkkkP T−−
Φ−+Φ= /1/ 1
( ) ( ) 





=++=
∞→∞→
2212
1211
1/1lim/lim
pp
pp
kkPkkP
kk
( ) 





=+
∞→
2212
1211
/1lim
mm
mm
kkP
k
  
T
TTT
TT
mm
mmT
pp
pp
Q
w
−−
ΦΦ






−




















−










 −
=





1
01
2/
2/4/
10
1 2
23
34
2212
1211
2212
1211
1
σ
For Piecewise (between samples) Constant White Noise acceleration model
( ) ( )
( ) 







−+−
+−−+−
=





−−
−−
22
22
23
2212
23
2212
24
22
2
1211
1212221211
12111111
2/
2/4/2
1
11
ww
ww
TmTmTm
TmTmTmTmTm
mkmmk
mkmk
σσ
σσ


22
1212
23
221211
24
22
2
121111
2/
4/2
w
w
w
Tmk
TmTmk
TmTmTmk
σ
σ
σ
=
−=
+−=
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 2)

178. 179
EstimatorsSOLO
( )11
2
1111 1/ kkm P −= σ
12
22
12 / kTm wσ=
( ) 121211
22
121122 2//2// mkTkTTmkm w +=+= σ
We obtained the following 5 equations with 5 unknowns: k11, k12, m11, m12, m22
( )11
2
1212 1/ kkm P −= σ
( )2
111111 / Pmmk σ+=1
( )2
111212 / Pmmk σ+=2
4/2
24
22
2
121111 wTmTmTmk σ+−=3
2/
23
221211 wTmTmk σ−=4
22
1212 wTmk σ=5
Substitute the results obtained from and in1 2 34 5
( ) ( ) ( ) ( )
  

  
 4/
11
2
2
12
2
11
2
12
12112
11
2
12
11
2
2
11
24
1212
22
22
12121111
14121
2
1
w
w
T
mkT
P
m
m
P
m
P
mk
P
k
k
T
k
k
k
T
k
T
k
kT
k
k
σ
σ
σσσσ
=
−
+
−






+−
−
=
−
3
0
4
1
2
2
12
2
121112
2
11 =++− kTkkTkTk
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 3)

179. 180
EstimatorsSOLO
We obtained: 0
4
1
2
2
12
2
121112
2
11 =++− kTkkTkTk
Kalata introduced the α, β parameters defined as: Tkk 1211 :: == βα
and the previous equation is written as function of α, β as:
0
4
1
2 22
=++− ββαβα
which can be used to write α as a function of β:
2
2
β
βα −=
( ) 12
22
11
2
12
12
1 k
T
k
k
m wP σσ
=
−
=
We obtained:
( )
T
TTm w
P
β
σ
α
σ
β
22
2
12
1
=
−
=
( )
2
2
242
:
1
λ
σ
σ
α
β
==
− P
wT
P
wT
σ
σ
λ
2
:= Target Maneuvering Index proportional to the ratio of:
Motion Uncertainty:
2
22
Twσ
Observation Uncertainty: 2
Pσ
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 4)

180. 181
EstimatorsSOLO
0
2
=−+ λβ
λ
β
The positive solution for from the above equation is:β ( )λλλβ 8
22
1 2
++−=
Therefore: ( ) ( )λλλ
λ
λλλλλβ 84
4
84
4
1 222
+−+=+−+=
and:
( )( )λλλλλλλ
λ
β
α 8428168
16
1
11 222
2
2
++−++++−=−=
( )( )λλλλλα 848
8
1 22
++−+−=
2
2
β
βα −=We obtained:
( )
2
2
242
:
1
λ
σ
σ
α
β
==
− P
wT
and:
( ) ( )2
22
2
2/12/21 β
β
ββ
β
λ
−
=
+−
=
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 5)

181. 182
EstimatorsSOLO
We found
( ) ( )
( ) 





−−
−−
=





1212221211
12111111
2212
1211
1
11
mkmmk
mkmk
pp
pp
( )11
2
1111 1/ kkm P −= σ
( )11
2
1212 1/ kkm P −= σ
( ) 121211
22
121122
2//
2//
mkTk
TTmkm w
+=
+= σ
( ) 2
11111111 1 Pkmkp σ=−=
( ) 2
12121112 1 Pkmkp σ=−=
( )
( )
α
σ
β
βα
−





−=
−=
−+=
12
2//
2//
2
121211
121212121122
P
T
TT
mkTk
mkmkTkp
2
11 Pp σα=
2
12 P
T
p σ
β
=
( )
( )
2
222
1
2/
P
T
p σ
α
βαβ
−
−
=
&
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 6)

182. 183
Estimators
( )( )λλλλλα 848
8
1 22
++−+−=
SOLO
We found
( ) ( )λλλ
λ
λλλλλβ 84
4
84
4
1 222
+−+=+−+=
α, β gains, as function of λ in semi-log and log-log scales
α - β (2-D) Filter with Piecewise Constant White Noise Acceleration Model (continue – 7)

183. 184
EstimatorsSOLO
  
T
T
q
TT
TT
mm
mmT
pp
pp
Q −−
ΦΦ






−




















−










 −
=





1
01
2/
2/3/
10
1
2
23
2212
1211
2212
1211
1
For White Noise acceleration model
( ) ( )
( ) 







−+−
+−−+−
=





−−
−−
qTmqTmTm
qTmTmqTmTmTm
mkmmk
mkmk
22
2
2212
2
2212
3
22
2
1211
1212221211
12111111
2/
2/3/2
1
11


qTmk
qTmTmk
qTmTmTmk
=
−=
+−=
1212
2
221211
3
22
2
121111
2/
3/2
α - β (2-D) Filter with White Noise Acceleration Model
( )








=
TT
TT
qkQ
2/
2/3/
2
23

184. 185
EstimatorsSOLO
( )11
2
1111 1/ kkm P −= σ
1212 / kqTm =
( ) 121211121122 2//2// mkTkqTTmkm +=+=
We obtained the following 5 equations with 5 unknowns: k11, k12, m11, m12, m22
( )11
2
1212 1/ kkm P −= σ
( )2
111111 / Pmmk σ+=1
( )2
111212 / Pmmk σ+=2
3/2 3
22
2
121111 qTmTmTmk +−=3
2/2
221211 qTmTmk −=4
qTmk =12125
Substitute the results obtained from and in1 2 34 5
( ) ( ) ( ) ( )
  

  
 3/
11
2
2
12
2
11
2
12
12112
11
2
12
11
2
2
11
3
1212
22
12121111
13121
2
1
qT
mkqT
P
m
m
P
m
P
mk
P
k
k
T
k
k
k
T
k
T
k
kT
k
k
=
−
+
−






+−
−
=
−
σσσσ3
0
6
1
2
2
12
2
121112
2
11 =++− kTkkTkTk
α - β (2-D) Filter with White Noise Acceleration Model (continue – 1)

185. 186
EstimatorsSOLO
We obtained: 0
6
1
2
2
12
2
121112
2
11 =++− kTkkTkTk
The α, β parameters defined as: Tkk 1211 :: == βα
and the previous equation is written as function of α, β as:
0
6
1
2 22
=++− ββαβα
which can be used to write α as a function of β:
212
2
2
ββ
βα −+=
α
βσ
β −
=
−
===
1
/
1/ 11
2
12
12
12
T
k
k
T
qT
k
qT
m P
We obtained:
2
2
32
:
1
c
P
qT
λ
σα
β
==
−
α - β (2-D) Filter with White Noise Acceleration Model (continue – 2)
2
2
22
:
12
2
2
1
1
cλ
β
β
β
β
α
β
=
+−+
=
−
The equation for solving β is:
which can be solved numerically.

186. 187
EstimatorsSOLO
We found
( ) ( )
( ) 





−−
−−
=





1212221211
12111111
2212
1211
1
11
mkmmk
mkmk
pp
pp
( )11
2
1111 1/ kkm P −= σ
( )11
2
1212 1/ kkm P −= σ
( ) 12121122 2// mkTkm +=
( ) 2
11111111 1 Pkmkp σ=−=
( ) 2
12121112 1 Pkmkp σ=−=
( )
( )
α
σ
β
βα
−





−=
−=
−+=
12
2//
2//
2
121211
121212121122
P
T
TT
mkTk
mkmkTkp
2
11 Pp σα=
2
12 P
T
p σ
β
=
( )
( )
2
222
1
2/
P
T
p σ
α
βαβ
−
−
=
&
α - β Filter with White Noise Acceleration Model (continue – 3)

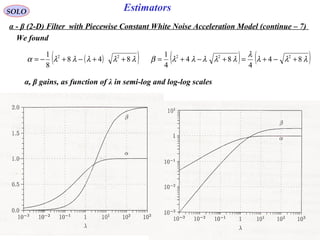
187. 188
Estimators

w
x
x
x
x
x
x
td
d
BA










+




















=










1
0
0
000
100
010





SOLO
We want to find the steady-state form of the filter for
Assume that only the position measurements are available
[ ] { } { } kjjkkk
k
kkkk RvvEvEv
x
x
x
vxHz δ==+










=+= ++++
+
++++ 1111
1
1111 0&001


Discrete System



+=
Γ+Φ=
++++
+
1111
1
kkkk
kkkkk
vxHz
wxx { }
[ ] { }










==+=
==










+










=
++++++
ΓΦ
+
+
kjP
T
jkkkk
H
k
kjw
T
jkkkkk
vvERvxz
wwEQwT
T
xT
TT
x
k
kk
δσ
δσ
2
111111
2
22
1
&001
&
1
2/
100
10
2/1
1

  
α – β - γ (3-D) Filter with Piecewise Constant Wiener Process Acceleration Model
x
x
x


- position
- velocity
- acceleration

188. 189
SOLO
Estimators
Piecewise (between samples) Constant White Noise acceleration model
( ) ( ) ( ){ } ( ) ( ) ( ) [ ]12/
1
2/
2
2
00 TTT
T
qlqkllwkwEk kl
TTT










=ΓΓ=ΓΓ δ
( ) ( ) ( ){ } ( )










=ΓΓ
12/
2/
2/2/2/
2
23
234
0
TT
TTT
TTT
qllwkwEk TT
Guideline for Choice of Process Noise Intensity
For this model q should be of the order of maximum acceleration increment over a
sampling period ΔaM.
A practical range is 0.5 ΔaM ≤ q ≤ ΔaM.
α – β - γ (3-D) Filter with Piecewise Constant Wiener Process Acceleration Model
(continue – 1)

189. 190
SOLO
Estimators
The Target Maneuvering Index is defined as for α – β Filter as:
P
wT
σ
σ
λ
2
:=
α – β - γ (3-D) Filter with Piecewise Constant Wiener Process Acceleration Model
(continue – 2)
The three equations that yield the optimal steady-state gains are:
( )
2
2
14
λ
α
γ
=
−
( ) ααβ −−−= 1422 or: 2/2 ββα −=
α
β
γ
2
=
This system of three nonlinear equations can be solved numerically.
The corresponding update state covariance expressions are:
( )
( )
( )
( )
( )
( )
2
433
2
213
2
323
2
12
2
222
2
11
14
2
14
2
18
428
PP
PP
PP
T
p
T
p
T
p
T
p
T
pp
σ
α
γβγ
σ
γ
σ
α
γββ
σ
β
σ
α
αβγβα
σα
−
−
==
−
−
==
−
−−+
==

190. 191
SOLO
Estimators
α – β - γ Filter gains as functions of λ in semi-log and log-log scales:
α – β - γ (3-D) Filter with Piecewise Constant Wiener Process Acceleration Model
(continue – 3)
Table of Content

191. 192
SOLO
Estimators
Optimal Filtering
An “Optimal Filter” is said to be optimal in some specific sense.
1. Minimum Mean-Square Error (MMSE)
{ } ( )∫ −=− nnnnn
x
nnn
x
xdZxpxxZxxE
nn
:0
2
:0
2
|ˆmin|ˆmin
Solution: { } ( )∫== nnnnnnn xdZxpxZxEx :0:0 ||ˆ
2. Maximum a Posteriori (MAP)
( ) ( ){ }nxxxx
nn
x
xIEZxp nnn
nn
ς≤−
−⇔ ˆ::0 1min|modemin
Where is an indicator function and ζ is a small scalar.( )nxI
3. Maximum Likelihood (ML) ( )nn
y
xyp
n
|max
4. Minimax: Median of Posterior ( )nn Zxp :0|
5. Minimum Conditional Inaccuracy
( ) ( ){ } ( )
( )∫=− ydxd
yxp
yxpyxpE
x
yxp
x |ˆ
1
log|ˆmin|ˆlogmin ,

192. 193
SOLO
Estimators
Optimal Filtering
An “Optimal Filter” is said to be optimal in some specific sense.
6. Minimum Conditional KL Divergence
( ) ( )
( ) ( )∫= ydxd
xpyxp
yxp
yxpKL
|ˆ
,
log,
7. Minimum Free Energy: It is a lower bound of
maximum log-likelihood, which is aimed to
minimize
( ) ( ) ( ){ } ( )
( )
( ) ( ) ( ){ }xQE
yxP
xQ
EyxPEPQ xQxQxQ log
|
log|log, −






=−=F
where Q (x) is an arbitrary distribution of x.
The first term is called Kulleback – Leibler (KL) divergence between distribution Q (x)
and P (x|y), the second term is entropy w.r.t. Q (x).
Table of Content

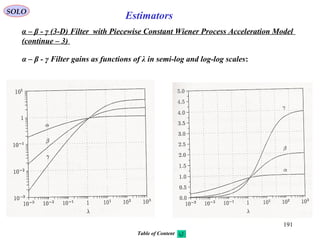
193. 194
SOLO Estimators
Continuous Filter-Smoother Algorithms
Problem - Choose w(t) and x(t0) to minimize:
( ) ( ) { }∫ −− −+−+−+−=
f
f
t
t
QRSffS
dtwwxHzxtxxtxJ
0
11
0
2222
00
2
1
2
1
2
1
subject to: ( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( )tvtxtHtz +=
and given: ( ) ( ) ( ) ( ) ( ) ( ) ( )tGtFtHtQtRSSxxtwtz ff ,,,,,,,,,, 00
Smoothing Interpretation
are noisy observations of Hx, i.e.:
v(t) is zero-mean white noise vector with density matrix R(t).
w(t) are random forcing functions, i.e., white noise vector with prior mean w(t)
and density matrix Q(t).
(x0, P0) are mean and covariance of initial state vector from independent observations
before test
(xf, Pf) are mean and covariance of final state vector from independent observations
after test
( ) ( )[ ] ( )[ ]T
S
xtxSxtxxtx 00000
2
00
2
1
:
2
1
0
−−=−where

194. 195
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem :
( ) nHamiltonia:H =++−+−= −− wGxFwwxHz T
QR
λ
22
11
2
1
2
1
Euler-Lagrange equations:
( )
( )







+−=
∂
∂
=
−−=
∂
∂
−=
−
−
GQww
w
H
FHRxHz
x
H
TT
TTT
λ
λλ
1
1
0

Two-Point Boundary Value Problem
Define:
( ) ( )[ ]
( ) ( )[ ]






−=
∂
∂
=
−−=
∂
∂
−=
f
T
ff
t
f
T
T
t
T
Sxtx
x
J
t
Sxtx
x
J
t
f
λ
λ 0000
0
Boundary equations:
λT
GQww −=
( ) ( )
( ) ( )
( ) ( ) ( ) ( )ttPtxtx
tSxtx
tSxtx
FF
tt
SP
ffff
λ
λ
λ
−=⇒




−=
+= →
=−
−
−
0
1
00:
0
1
000
1
zRHFxHRH TTT 11 −−
+−−= λλ
( ) ( )

w
T
GQwGxFtx λ−+=
td
d
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

Assumed solution
Forward

195. 196
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
Differentiate and use previous equations
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ]
( )
( ) ( )
( ) ( ) ( )[ ]
( )
( ) ( )twGtGQGttPtxF
tzRHtFttPtxHRHtPttPtx
ttPttPtxtx
T
tx
FF
TT
tx
FF
T
FFF
FFF
+−−=








+−−−⋅−−=
−−=
−−
λλ
λλλ
λλ
  
  


11
( ) ( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( ) ( ) ( )[ ] ( )ttPHRHtPtPFFtPtP
twGtxHtzRHtPtxFtx
F
T
FF
T
FF
F
T
FFF
λ1
1
−
−
+−−=
−−−−


( ) ( ) ( ) ( )ttPtxtx FF λ−=First Way, Assumption 1 .
( ) ( )
( ) ( )



+=
−=
−
−
ffff tSxtx
tSxtx
λ
λ
1
0
1
000
or

196. 197
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 2) :
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( ) ( ) ( )[ ] ( )ttPHRHtPtPFFtPtP
twGtxHtzRHtPtxFtx
F
T
FF
T
FF
F
T
FFF
λ1
1
−
−
+−−=
−−−−


( ) ( )
( ) ( )



+=
−=
−
−
ffff tSxtx
tSxtx
λ
λ
1
0
1
000
We want to have xF(t) independent on λ(t). This is obtain by choosing
( ) ( ) ( ) ( ) ( ) ( ) 1
000
1 −−
==−+= SPtPtPHRHtPtPFFtPtP FF
T
FF
T
FF

( ) ( ) ( ) ( ) ( )[ ] ( ) ( )
( ) ( ) 1
00
: −
=
=+−+=
RHtPtK
xtxtwGtxHtztKtxFtx
T
FF
FFFFF

Therefore
Let substitute the results in the equation( )tλ
( ) ( ) ( ) ( )[ ] ( ) ( )
( )

( ) ( ) ( )[ ]
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( )[ ]ffFffFfffffFffFffF
F
T
T
RHtP
F
TT
FF
T
xtxPtPttPxtxtxtxttP
txHtzRHtHKF
tzRHtFttPtxHRHt
T
F
−+=⇒−−=−=
−+








−−=
+−−−=
−
−
−−
−
1
1
11
1
λλλ
λ
λλλ
( ) ( ) ( ) ( )ttPtxtx FF λ−=First Way, Assumption 1 (continue – 1) .

197. 198
SOLO Estimators
Continuous Filter-Smoother Algorithms
Problem - Choose w(t) and x(t0) to minimize:
( ) ( ) { }∫ −− −+−+−+−=
f
f
t
t
QRSffS
dtwwxHzxtxxtxJ
0
11
0
2222
00
2
1
2
1
2
1
subject to: ( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( )tvtxtHtz +=
Forward Covariance Filter
( ) ( ) ( ) ( ) ( )[ ] ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) 1
00
1
00
: −
−
=
=−+=
=+−+=
RHtPtKwhere
PtPtPHRHtPtPFFtPtP
xtxtwGtxHtztKtxFtx
T
FF
FF
T
FF
T
FF
FFFFF


Store xF(t) and PF(t)
Backward Information Filter (τ = tf – t)
( )[ ] ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]ffFffFfF
TT
F xtxPtPttxHtzRHtHtKF
td
d
d
d
−+=−−−−=−=
−− 11
λλ
λ
τ
λ
Summary of First Assumption – Forward then Backward Algorithms
where = Estimate of w(t)( ) ( ) ( )tGQtwtw T
λ−=
= Smoothed Estimate of x(t)( ) ( ) ( )tPtxtx FF λ−=

198. 199
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem :
( ) nHamiltonia:H =++−+−= −− wGxFwwxHz T
QR
λ
22
11
2
1
2
1
Euler-Lagrange equations:
( )
( )







+−=
∂
∂
=
−−=
∂
∂
−=
−
−
GQww
w
H
FHRxHz
x
H
TT
TTT
λ
λλ
1
1
0

Two-Point Boundary Value Problem
Define:
( ) ( )[ ]
( ) ( )[ ]






−=
∂
∂
=
−−=
∂
∂
−=
f
T
ff
t
f
T
T
t
T
Sxtx
x
J
t
Sxtx
x
J
t
f
λ
λ 0000
0
Boundary equations:
λT
GQww −=
zRHFxHRH TTT 11 −−
+−−= λλ
( ) ( )[ ]
( ) ( )[ ]
( ) ( ) ( ) ( )txtStt
Sxtx
x
J
t
Sxtx
x
J
t
FF
f
T
ff
t
f
T
T
t
T
f
−=⇒







−=
∂
∂
=
−−=
∂
∂
−=
λλ
λ
λ 0000
0
Second Way, Assumption 2:
Forward

199. 200
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
Differentiate and use previous equations
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ){ }
( ) ( ) ( ) ( )[ ] ( )tzRHtxtStFtxHRH
twGtxtStGQGtxFtStxtSt
txtStxtStt
T
FF
TT
FF
T
FFF
FFF
11 −−
+−−−=
+−−⋅−−=
−−=
λ
λλ
λλ


( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ] ( )txHRHtSGQGtStSFFtStS
twGtStzRHtGQGtStFt
T
F
T
FF
T
FF
F
T
F
T
FF
T
F
1
1
−
−
−+++=
−−++

 λλλ
( ) ( ) ( ) ( )txtStt FF −=λλSecond Way, Assumption 2
( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
or

200. 201
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ] ( )txHRHtSGQGtStSFFtStS
twGtStzRHtGQGtStFt
T
F
T
FF
T
FF
F
T
F
T
FF
T
F
1
1
−
−
−+++=
−−++

 λλλ
( ) ( ) ( ) ( )txtStt FF −=λλSecond Way, Assumption 2
( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
We want to have λF(t) independent on x(t). This is obtain by choosing
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )tSQGtC
StSHRHtCQtCtSFFtStS
F
T
F
F
T
FFF
T
FF
=
=+−−−= −−
:
00
11
Therefore
( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) 000
1
xSttwGtStzRHttCGFt FF
T
F
T
FF =+++−= −
λλλ
Let substitute the results in the equation( )tx
( ) ( ) ( ) ( ) ( )[ ] ( )
( )[ ] ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]fffFffFfffFfFffff
F
T
F
FF
T
xStStStxtxtStxStxS
tQGtwGtxtCGF
twGtxtStGQGtxFtx
++=⇒−+=
−++=
+−−=
−
λλ
λ
λ
1


201. ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )tSQGtC
StSHRHtCQtCtSFFtStS
xSttwGtStzRHttCGFt
F
T
F
F
T
FFF
T
FF
FF
T
F
T
FF
=
=+−−−=
=+++−=
−−
−
:
00
11
000
1

 λλλ
202
SOLO Estimators
Continuous Filter-Smoother Algorithms
Problem - Choose w(t) and x(t0) to minimize:
( ) ( ) { }∫ −− −+−+−+−=
f
f
t
t
QRSffS
dtwwxHzxtxxtxJ
0
11
0
2222
00
2
1
2
1
2
1
subject to: ( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( )tvtxtHtz +=
Forward InformationFilter
Store λF(t) and SF(t)
Backward Information Smoother (τ = tf – t)
Summary of Second Assumption – Forward then Backward Algorithms
( )[ ] ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]fffFffFfF
T
F xStStStxtQGtwGtxtCGF
td
xd
d
xd
++=⇒−−+−=−=
−
λλ
τ
1
where = Estimate of w(t)( ) ( ) ( )tGQtwtw T
λ−=
= Smoothed Estimate of x(t)( ) ( ) ( )tPtxtx FF λ−=

202. 203
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem :
( ) nHamiltonia:H =++−+−= −− wGxFwwxHz T
QR
λ
22
11
2
1
2
1
Euler-Lagrange equations:
( )
( )







+−=
∂
∂
=
−−=
∂
∂
−=
−
−
GQww
w
H
FHRxHz
x
H
TT
TTT
λ
λλ
1
1
0

Two-Point Boundary Value Problem
Define:
( ) ( )[ ]
( ) ( )[ ]






−=
∂
∂
=
−−=
∂
∂
−=
f
T
ff
t
f
T
T
t
T
Sxtx
x
J
t
Sxtx
x
J
t
f
λ
λ 0000
0
Boundary equations:
λT
GQww −=
zRHFxHRH TTT 11 −−
+−−= λλ
( )[ ] ( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( )ttPtxtx
tPtSxtx
tPtSxtx
BB
ffffff
λ
λλ
λλ
+=⇒




==−
==−−
−
−
1
000
1
000
Third Way, Assumption 3:
Backward

203. 204
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
Differentiate and use previous equations
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) ( ){ }
( ) ( ) ( )[ ] ( ) ( )twGtGQGttPtxF
tzRHtFttPtxHRHtPttPtx
ttPttPtxtx
T
BB
TT
BB
T
BBB
BBB
+−+=
+−+−⋅++=
++=
−−
λλ
λλλ
λλ
11

( ) ( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( ) ( ) ( )[ ] ( )ttPHRHtPGQGFtPtPFtP
twGtxHtzRHtPtFxtx
B
T
B
TT
BBB
B
T
BBB
λ1
1
−
−
+−++−=
−−+−


( ) ( ) ( ) ( )ttPtxtx BB λ+=Third Way, Assumption 3
( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
or

204. 205
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ
 ( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
We want to have xB(t) independent on λ(t). This is obtain by choosing
Therefore
Let substitute the results in the equation( )tλ
( ) ( ) ( ) ( )ttPtxtx BB λ+=Third Way, Assumption 3
( ) ( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( ) ( ) ( )[ ] ( )ttPHRHtPGQGFtPtPFtP
twGtxHtzRHtPtFxtx
B
T
B
TT
BBB
B
T
BBB
λ1
1
−
−
+−++−=
−−+−


( ) ( ) ( ) ( ) ( ) ( )
( ) 1
: −
=
=−+−−=−
RHtPK
PtPtKRtKGQGFtPtPFtP
T
BB
ffBBB
TT
BBB

( ) ( ) ( ) ( ) ( )[ ] ( ) ( ) ffBBBBB xtxtwGtxHtztKtFxtx =−−+−=− 
( ) ( ) ( ) ( )[ ] ( ) ( )
( )

( ) ( ) ( )[ ]
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( )[ ]00
1
00000000000
1
11
1
xtxPtPttPxtxtxtxttP
txHtzRHtHKF
tzRHtFttPtxHRHt
BBBBB
B
T
T
RHtP
B
TT
BB
T
T
B
−+−=⇒−+−=+−=
−+








+−=
+−+−=
−
−
−−
−
λλλ
λ
λλλ

205. ( ) ( ) ( ) ( ) ( )[ ] ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
( ) 1
: −
=
=−+−−=−
=−−+−=−
RHtPK
PtPtKRtKGQGFtPtPFtP
xtxtwGtxHtztKtFxtx
T
BB
ffBBB
TT
BBB
ffBBBBB


206
SOLO Estimators
Continuous Filter-Smoother Algorithms
Problem - Choose w(t) and x(t0) to minimize:
( ) ( ) { }∫ −− −+−+−+−=
f
f
t
t
QRSffS
dtwwxHzxtxxtxJ
0
11
0
2222
00
2
1
2
1
2
1
subject to: ( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( )tvtxtHtz +=
Backward Covariance Filter (τ = tf – t)
Store xB(t) and PB(t)
Forward Covariance Smoother
Summary of Third Assumption – Backward then Forward Algorithms
( ) ( ) ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]00
1
000
1
xtxPtPttxHtzRHtHKFt BBB
TT
B −+−=−++−=
−−
λλλ
where = Estimate of w(t)( ) ( ) ( )tGQtwtw T
λ−=
= Smoothed Estimate of x(t)( ) ( ) ( )tPtxtx FF λ−=

206. 207
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem :
( ) nHamiltonia:H =++−+−= −− wGxFwwxHz T
QR
λ
22
11
2
1
2
1
Euler-Lagrange equations:
( )
( )







+−=
∂
∂
=
−−=
∂
∂
−=
−
−
GQww
w
H
FHRxHz
x
H
TT
TTT
λ
λλ
1
1
0

Two-Point Boundary Value Problem
Define:
( ) ( )[ ]
( ) ( )[ ]






−=
∂
∂
=
−−=
∂
∂
−=
f
T
ff
t
f
T
T
t
T
Sxtx
x
J
t
Sxtx
x
J
t
f
λ
λ 0000
0
Boundary equations:
λT
GQww −=
zRHFxHRH TTT 11 −−
+−−= λλ
( ) ( )[ ]
( ) ( )[ ]
( ) ( ) ( ) ( )txtStt
Sxtx
x
J
t
Sxtx
x
J
t
BB
f
T
ff
t
f
T
T
t
T
f
+=⇒







−=
∂
∂
=
−−=
∂
∂
−=
λλ
λ
λ 0000
0
Fourth Way, Assumption 4:
Backward

207. 208
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
Differentiate and use previous equations
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ){ }
( ) ( ) ( ) ( )[ ] ( )tzRHtxtStFtxHRH
twGtxtStGQGtxFtStxtSt
txtStxtStt
T
BB
TT
BB
T
BBB
BBB
11 −−
++−−=
++−⋅++=
++=
λ
λλ
λλ


( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ] ( )txHRHtSGQGtStSFFtStS
twGtStzRHtGQGtStFt
T
B
T
BB
T
BB
B
T
B
T
BB
T
B
1
1
−
−
−+−−−=
+−−+

 λλλ
( ) ( ) ( ) ( )txtStt BB +=λλFourth Way, Assumption 4
( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
or

208. 209
SOLO Estimators
Continuous Filter-Smoother Algorithms
Solution to the Problem (continue – 1) :
( )
( )
( )
( ) 





+













−−
−
=





−−
zRH
wG
t
tx
FHRH
GQGF
t
tx
TTT
T
11
λλ

( ) ( ) ( ) ( )txtStt BB +=λλFourth Way, Assumption 4
( ) ( )[ ]
( ) ( )[ ]



−=
−−=
f
T
fff
T
TT
Sxtxt
Sxtxt
λ
λ 0000
We want to have λF(t) independent on x(t). This is obtain by choosing
Therefore
( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) fffBB
T
F
T
BB xSttwGtStzRHttCGFt −=+−−=− −
λλλ 1
Let substitute the results in the equation( )tx
( ) ( ) ( ) ( ) ( )[ ] ( )
( )[ ] ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]000
1
0000000000 xStStStxtxtStxStxS
tQGtwGtxtCGF
twGtxtStGQGtxFtx
BBBB
B
T
B
BB
T
+−+=⇒+−=
−+−=
++−=
−
λλ
λ
λ
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ] ( )txHRHtSGQGtStSFFtStS
twGtStzRHtGQGtStFt
T
B
T
BB
T
BB
B
T
B
T
BB
T
B
1
1
−
−
−+−−−=
+−−+

 λλλ
( ) ( ) ( ) ( ) ( ) ( )
( )tSQGC
StSHRHtCQtCtSFFtStS
B
T
B
ffB
T
B
T
BB
T
BB
=
=+−=− −−
:
11

209. ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
( )tSQGC
StSHRHtCQtCtSFFtStS
xSttwGtStzRHttCGFt
B
T
B
ffB
T
B
T
BB
T
BB
fffBB
T
F
T
BB
=
=+−=−
−=+−−=−
−−
−
:
11
1

 λλλ
210
SOLO Estimators
Continuous Filter-Smoother Algorithms
Problem - Choose w(t) and x(t0) to minimize:
( ) ( ) { }∫ −− −+−+−+−=
f
f
t
t
QRSffS
dtwwxHzxtxxtxJ
0
11
0
2222
00
2
1
2
1
2
1
subject to: ( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( )tvtxtHtz +=
Backward InformationFilter (τ = tf – t)
Store λB(t) and SB(t)
Forward Information Smoother
Summary of Fourth Assumption – Backward then Forward Algorithms
( ) ( )[ ] ( ) ( ) ( )[ ] ( ) ( )[ ] ( )[ ]000
1
000 xStStStxtQGtwGtxtCGFtx BBB
T
B +−+=−+−=
−
λλ
where = Estimate of w(t)( ) ( ) ( )tGQtwtw T
λ−=
= Smoothed Estimate of x(t)( ) ( ) ( )tPtxtx FF λ−=
Table of Content

210. 211
EstimatorsSOLO
References
Minkoff, J., “Signals, Noise, and Active Sensors”, John Wiley & Sons, 1992
Sage, A. P., Melsa, J. L., “Estimation Theory with Applications to Communication and
Control”, McGraw Hill, 1971
Gelb, A.,Ed., written by the Technical Staff, The Analytic Sciences Corporation,
“Applied Optimal Estimation”, M.I.T. Press, 1974
Bryson, A.E. Jr., Ho, Y-C., “Applied Optimal Control”, Ginn & Company, 1969
Kailath, T., Sayed, A.H., Hassibi, B, “Linear Estimators”, Prentice Hall, 2000
Sage, A. P., “Optimal Systems Control”, Prentice-Hall, 1968, 1st
Ed.,
Ch.8, Optimal State Estimation
Sage, A. P., White, C.C., III “Optimal Systems Control”, Prentice-Hall, 1977, 2nd
Ed.,
Ch.8, Optimal State Estimation
Y. Bar-Shalom, T.E. Fortmann, “Tracking and Data Association”, Academic Press, 1988
Y. Bar-Shalom, Xiao-Rong Li., “Multitarget-Multisensor Tracking: Principles and
Techniques”, YBS Publishing, 1995
Haykin, S. “Adaptive Filter Theory”, Prentice Hall, 4th
Ed., 2002

211. 212
EstimatorsSOLO
References (continue – 1(
Minkler, G., Minkler, J., “Theory and Applications of Kalman Filters”, Magellan, 1993
Stengel, R. F., “Stochastic Optimal Control – Theory and Applications”, John Wiley &
Sons, 1986
Kailath, T., “Lectures on Wiener and Kalman Filtering”, Springer-Verlag, 1981
Anderson, B. D. O., Moore, J. B., “Optimal Filtering”, Prentice-Hall, 1979
Deutch, R., “System Analysis Techniques”, Prentice Hall, 1969, ch. 6
Chui, C. K., Chen, G., “Kalman Filtering with Real Time Applications”, Springer-Verlag,
1987
Catlin, D. E., “Estimation, Control, and the Discrete Kalman Filter”, Springer-Verlag,
1989
Haykin, S., Ed., “Kalman Filtering and Neural Networks”, John Wiley & Sons, 2001
Zarchan, P., Musoff, H., “Fundamentals of Kalman Filtering – A Practical Approach”,
AIAA, Progress in Astronautics & Aeronautics, vol. 190, 2000
Brookner, E., “Tracking and Kalman Filtering Made Easy”, John Wiley & Sons, 1998

212. 213
EstimatorsSOLO

213. 214
EstimatorsSOLO
References
Arthur E. Bryson Jr.
Professor Emeritus
Aeronautics and Astronautics
Phone:650.857.1354
E-mail:bryson@sun-valley.stanford.edu
Andrew P. Sage Thomas Kailath
1935-
From left-to-right: Sam Blackman, Oliver Drummond,
Yaakoov Bar-Shalom and Rabinder Madan
Dr. Simon Haykin
University Professor
Director Adaptive Systems Laboratory
McMaster University, CRL-105
1280 Main Street West
Hamilton, ON
Canada L8S 4L7
Tel: (905) 525-9140 ext. 24809
Fax: (905) 521-2922
Table of Content

214. January 10, 2015 215
SOLO
Technion
Israeli Institute of Technology
1964 – 1968 BSc EE
1968 – 1971 MSc EE
Israeli Air Force
1970 – 1974
RAFAEL
Israeli Armament Development Authority
1974 – 2013
Stanford University
1983 – 1986 PhD AA

215. 216
SOLO Review of Probability
Normal (Gaussian) Distribution
Karl Friederich Gauss
1777-1855
( )
( )
σπ
σ
µ
σµ
2
2
exp
,;
2
2





 −
−
=
x
xp
( ) ( )
∫
∞−





 −
−=
x
du
u
xP 2
2
2
exp
2
1
,;
σ
µ
σπ
σµ
( ) µ=xE
( ) σ=xVar
( ) ( )[ ]
( ) ( )






−=





 −
−=
=Φ
∫
∞+
∞−
2
exp
exp
2
exp
2
1
exp
22
2
2
σω
µω
ω
σ
µ
σπ
ωω
j
duuj
u
xjE
Probability Density Functions
Cumulative Distribution Function
Mean Value
Variance
Moment Generating Function

216. 217
SOLO Review of Probability
Moments
Normal Distribution ( ) ( ) ( )[ ]
σπ
σ
σ
2
2/exp
;
22
x
xpX
−
=
[ ] ( )


 −⋅
=
oddnfor
evennforn
xE
n
n
0
131 σ
[ ]
( )





+=
=−⋅
= +
12!2
2
2131
12
knfork
knforn
xE kk
n
n
σ
π
σ
Proof:
Start from: and differentiate k time with respect to a( ) 0exp 2
>=−∫
∞
∞−
a
a
dxxa
π
Substitute a = 1/(2σ2
) to obtain E [xn
]
( ) ( ) 0
2
1231
exp 12
22
>
−⋅
=− +
∞
∞−
∫ a
a
k
dxxax kk
k π
[ ] ( ) ( )[ ] ( ) ( )[ ]
( ) ( ) 12
!
0
122/
0
222221212
!2
2
exp
2
22
2/exp
2
2
2/exp
2
1
2
+
∞+
=
∞∞
∞−
++
=−=
−=−=
∫
∫∫
kk
k
k
k
xy
kkk
kdyyy
xdxxxdxxxxE
σ
πσ
σ
π
σ
σπ
σ
σπ
σ
  
Now let compute:
[ ] [ ]( )2244
33 xExE == σ
Chi-square

217. 218
SOLO Review of Probability
Normal (Gaussian) Distribution (continue – 1)
Karl Friederich Gauss
1777-1855
( ) ( ) ( )



−−−= −−
xxPxxPPxxp
T  12/1
2
1
exp2,; π
A Vector – Valued Gaussian Random Variable has the
Probability Density Functions
where
{ }xEx

= Mean Value
( )( ){ }T
xxxxEP

−−= Covariance Matrix
If P is diagonal P = diag [σ1
2
σ2
2
… σk
2
] then the components of the random vector
are uncorrelated, and
x

( )
( ) ( ) ( ) ( )
∏=
−
−





 −
−
=





 −
−




 −
−




 −
−
=






























−
−
−




























−
−
−
−=
k
i i
i
ii
k
k
kk
kk
k
T
kk
xxxxxxxx
xx
xx
xx
xx
xx
xx
PPxxp
1
2
2
2
2
2
2
2
2
22
1
2
1
2
11
22
11
1
2
2
2
2
1
22
11
2/1
2
2
exp
2
2
exp
2
2
exp
2
2
exp
0
0
2
1
exp2,;
σπ
σ
σπ
σ
σπ
σ
σπ
σ
σ
σ
σ
π



therefore the
components of the
random vector are
also independent

218. 219
SOLO Review of Probability
Monte Carlo Method
Monte Carlo methods are a class of computational algorithms that
rely on repeated random sampling to compute their results. Monte
Carlo methods are often used when simulating physical and
mathematical systems. Because of their reliance on repeated
computation and random or pseudo-random numbers, Monte Carlo
methods are most suited to calculation by a computer. Monte Carlo
methods tend to be used when it is infeasible or impossible to
compute an exact result with a deterministic algorithm.
The term Monte Carlo method was coined in the 1940s by
physicists Stanislaw Ulam, Enrico Fermi, John von Neumann,
and Nicholas Metropolis, working on nuclear weapon projects in
the Los Alamos National Laboratory
Stanislaw Ulam
1909 - 1984
Enrico - Fermi
1901 - 1954
John von Neumann
1903 - 1957 Nicholas Constantine Metropolis
(1915 –1999)

219. 220
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (Unknown Statistics)
{ } { } jimxExE ji ,∀==
Define
Estimation of the
Population mean
∑=
=
k
i
ik x
k
m
1
1
:ˆ
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to compute the sample mean, ,
and sample variance, , as estimates of the population mean, m, and variance, σ2
.
2
ˆkσ
kmˆ
( )
{ }
( ) ( ) ( )[ ] ( ) ( )[ ]
2
1
2
1
222
2
22222
1 11
2
1
2
2
11
2
1
2
11
1
1
1
1
1
21
11
2
1
ˆˆ2
1
ˆ
1
σσ
σσσ
k
k
kk
mkmkk
k
mmk
k
m
k
xx
k
Ex
k
xExE
k
mxmxE
k
mx
k
E
k
i
k
i
k
i
k
l
l
k
j
j
k
j
jii
k
k
i
ik
k
i
i
k
i
ki
−
=





−=






++−+++−−+=














+






−=






+−=






−
∑
∑
∑ ∑∑∑
∑∑∑
=
=
= ===
===
{ } { } jimxExE ji ,2222
∀+== σ
{ } { } mxE
k
mE
k
i
ik == ∑=1
1
ˆ
{ } { } { } jimxExExxE ji
tindependenxx
ji
ji
,2
,
∀==
Compute
Biased
Unbiased

220. 221
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 1)
{ } { } jimxExE ji ,∀==
Define
Estimation of the
Population mean
∑=
=
k
i
ik x
k
m
1
1
:ˆ
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to compute the sample mean, ,
and sample variance, , as estimates of the population mean, m, and variance, σ2
.
2
ˆkσ
kmˆ
( ) 2
1
2 1
ˆ
1
σ
k
k
mx
k
E
k
i
ki
−
=






−∑=
{ } { } jimxExE ji ,2222
∀+== σ
{ } { } mxE
k
mE
k
i
ik == ∑=1
1
ˆ
{ } { } { } jimxExExxE ji
tindependenxx
ji
ji
,2
,
∀==
Biased
Unbiased
Therefore, the unbiased estimation of the sample variance of the population is defined as:
( )∑=
−
−
=
k
i
kik mx
k 1
22
ˆ
1
1
:ˆσ since { } ( ) 2
1
22
ˆ
1
1
:ˆ σσ =






−
−
= ∑=
k
i
kik mx
k
EE
Unbiased

221. 222
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 2)
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to compute the sample mean, ,
and sample variance, , as estimates of the population mean, m, and variance, σ2
.
2
ˆkσ
kmˆ
{ } { } mxE
k
mE
k
i
ik == ∑=1
1
ˆ
{ } ( ) 2
1
22
ˆ
1
1
:ˆ σσ =






−
−
= ∑=
k
i
kik mx
k
EE

222. 223
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 3)
{ } { } mxE
k
mE
k
i
ik == ∑=1
1
ˆ { } ( ) 2
1
22
ˆ
1
1
:ˆ σσ =






−
−
= ∑=
k
i
kik mx
k
EEWe found:
Let Compute:
( ){ } ( )
( ){ } ( ) ( ){ }
( ){ } ( ){ } ( ){ }
k
mxEmxEmxE
k
mxmxEmxE
k
mx
k
Emx
k
EmmE
k
i
k
ij
j
ji
k
i
i
k
i
k
ij
j
ji
k
i
i
k
i
i
k
i
ikmk
2
1 1
00
1
2
2
1 11
2
2
2
1
2
1
22
ˆ
2
1
1
11
ˆ:
σ
σ
σ
=










−−+−=










−−+−=














−=














−=−=
∑ ∑∑
∑∑∑
∑∑
=
≠
==
=
≠
==
==

( ){ } k
mmE kmk
2
22
ˆ ˆ:
σ
σ =−=

223. 224
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 4)
Let Compute:
( ){ } ( ) ( )
( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )














−−
−
+−
−
−
+−
−
=














−−+−−+−
−
=














−−+−
−
=














−−
−
=−=
∑∑
∑
∑∑
==
=
==
2
22
11
2
2
2
1
22
2
2
1
2
2
2
1
22222
ˆ
ˆ
11
ˆ2
1
1
ˆˆ2
1
1
ˆ
1
1
ˆ
1
1
ˆ:2
σ
σ
σσσσσσ
k
k
i
i
k
k
i
i
k
i
kkii
k
i
ki
k
i
kik
mm
k
k
mx
k
mm
mx
k
E
mmmmmxmx
k
E
mmmx
k
Emx
k
EE
k
( )
( ){ } ( ){ } ( ){ } ( ){ }
( )
( ){ } ( )
( ){ }
( ){ }
( )
( ){ } ( ){ }
( )
( ){ } ( )
( ){ }
( ){ }
( )
( ){ } ( ){ }
( )
( ){ }
( )
( ){ }




    
  

  
k
k
k
i
i
k
k
i
i
k
k
k
i
i
k
k
i
i
k
k
k
i
i
k
k
k
k
i
i
k
k
k
i
k
ij
j
ji
k
k
i
i
mmE
k
k
mxE
k
mmE
mxE
k
mmEk
mxE
k
mxE
k
mmEk
mxE
k
mmE
mmE
k
k
mxE
k
mmE
mxEmxEmxE
kk
/
2
2
1
0
2
0
1
0
2
3
1
2
2
1
2
2
/
2
1
3
2
0
44
2
2
1
2
2
/
2
1 1
22
1
4
2
2
ˆ
2
222
22
22
4
2
ˆ
1
2
1
ˆ4
1
ˆ4
1
2
1
ˆ2
1
ˆ4
ˆ
11
ˆ4
1
1
σ
σσσ
σσ
σσ
µ
σ
σσ
σ
σσ
−
−
−−
−
−
−−
−
−
+
−
−
−−
−
−
+−
−
−
+
+−
−
+−
−
−
+












−−+−
−
≈
∑∑
∑∑∑
∑∑ ∑∑
==
===
==
≠
==
Since (xi – m), (xj - m) and are all independent for i ≠ j:( )kmm ˆ−

224. 225
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 4)
Since (xi – m), (xj - m) and are all independent for i ≠ j:( )kmm ˆ−
( )
( )
( ) ( ) ( )
( ){ }
( ) ( ) ( ) ( ) ( ) ( )
( ){ }4
2
2
4
22
4
44
2
4
44
2
2
2
4
2
4
2
42
ˆ
ˆ
11
7
11
2
1
2
1
2
ˆ
11
4
1
1
1
2
k
k
mmE
k
k
k
k
k
k
kk
k
k
k
mmE
k
k
kk
kk
k
k
k
−
−
+
−
+−
+
−
=
−
−
−
−
−
+
+−
−
+
−
+
−
−
+
−
≈
σ
µσσσ
σ
σσµ
σσ
kk
4
42
ˆ 2
σµ
σσ
−
≈ ( ){ }4
4 : mxE i −=µ
( )
( ){ } ( ){ } ( ){ } ( ){ }
( )
( ){ } ( )
( ){ }
( ){ }
( )
( ){ } ( ){ }
( )
( ){ } ( )
( ){ }
( ){ }
( )
( ){ } ( ){ }
( )
( ){ }
( )
( ){ }




    
  

  
k
k
k
i
i
k
k
i
i
k
k
k
i
i
k
k
i
i
k
k
k
i
i
k
k
k
k
i
i
k
k
k
i
k
ij
j
ji
k
k
i
i
mmE
k
k
mxE
k
mmE
mxE
k
mmEk
mxE
k
mxE
k
mmEk
mxE
k
mmE
mmE
k
k
mxE
k
mmE
mxEmxEmxE
kk
/
2
2
1
0
2
0
1
0
2
3
1
2
2
1
2
2
/
2
1
3
2
0
44
2
2
1
2
2
/
2
1 1
22
1
4
2
2
ˆ
2
222
22
22
4
2
ˆ
1
2
1
ˆ4
1
ˆ4
1
2
1
ˆ2
1
ˆ4
ˆ
11
ˆ4
1
1
σ
σσσ
σσ
σσ
µ
σ
σσ
σ
σσ
−
−
−−
−
−
−−
−
−
+
−
−
−−
−
−
+−
−
−
+
+−
−
+−
−
−
+












−−+−
−
≈
∑∑
∑∑∑
∑∑ ∑∑
==
===
==
≠
==

225. 226
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 5)
{ } { } mxE
k
mE
k
i
ik == ∑=1
1
ˆ
{ } ( ) 2
1
22
ˆ
1
1
:ˆ σσ =






−
−
= ∑=
k
i
kik mx
k
EE
We found:
( ){ } k
mmE kmk
2
22
ˆ ˆ:
σ
σ =−=
( ){ } ( )
k
mx
k
EE
k
i
kik
k
4
4
2
2
1
22222
ˆ
ˆ
1
1
ˆ:2
σµ
σσσσσ
−
≈














−−
−
=−= ∑=
( ){ }4
4 : mxE i −=µ
Kurtosis of random variable xi
Define
4
4
:
σ
µ
λ =
( ){ } ( ) ( )
k
mx
k
EE
k
i
kik
k
42
2
1
22222
ˆ
1
ˆ
1
1
ˆ:2
σλ
σσσσσ
−
≈














−−
−
=−= ∑=

226. 227
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 6)
[ ] ϕσσσ σσ =≤≤
2
ˆ
2
k
2
k
ˆ-0Prob n
For high values of k, according to the Central Limit Theorem the estimations of mean
and of variance are approximately gaussian random variables.
kmˆ
2
ˆkσ
We want to find a region around that
will contain σ2
with a predefined probability
φ as function of the number of iterations k.
2
ˆkσ
Since are approximately gaussian random
variables nσ is given by solving:
2
ˆkσ
ϕζζ
π
σ
σ
=





−∫
+
−
n
n
d2
2
1
exp
2
1 nσ φ
1.000 0.6827
1.645 0.9000
1.960 0.9500
2.576 0.9900
Cumulative Probability within nσ
Standard Deviation of the Mean for a
Gaussian Random Variable
22
k
22 1
ˆ-
1
σ
λ
σσσ
λ
σσ
k
n
k
n
−
≤≤
−
−
22
k
2
1
1
ˆ-1
1
σ
λ
σσ
λ
σσ 







−
−
≤≤







+
−
−
k
n
k
n

227. 228
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 7)
[ ] ϕσσσ σσ =≤≤
2
ˆ
2
k
2
k
ˆ-0Prob n
22
k
22 1
ˆ-
1
σ
λ
σσσ
λ
σσ
k
n
k
n
−
≤≤
−
−
22
k
2
1
1
ˆ-1
1
σ
λ
σσ
λ
σσ 







−
−
≤≤







+
−
−
k
n
k
n
22
ˆ
1
2
k
σ
λ
σσ
k
−
=
22
k
2 1
1ˆ
1
1 σ
λ
σσ
λ
σσ 






 −
−≥≥






 −
+
k
n
k
n







 −
−
≥≥







 −
+
k
n
k
n
1
1
ˆ
1
1
2
2
k
2
λ
σ
σ
λ
σ
σσ
k
n
k
n
1
1
:ˆ:
1
1
k
−
−
=≥≥=
−
+
λ
σ
σσσ
λ
σ
σσ

228. 229
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 8)

229. 230
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 9)

230. 231
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 10)
k
n
k
n
kk 1ˆ
1
:&
1ˆ
1
:
00
−
−
=
−
+
=
λ
σ
σ
λ
σ
σ
σσ
Monte-Carlo Procedure
Choose the Confidence Level φ and find the corresponding nσ
using the normal (gaussian) distribution.
nσ φ
1.000 0.6827
1.645 0.9000
1.960 0.9500
2.576 0.9900
1
Run a few sample k0 > 20 and estimate λ according to2
( )
( )
2
1
2
0
1
4
0
0
0
0
0
0
ˆ
1
ˆ
1
:ˆ






−
−
=
∑
∑
=
=
k
i
ki
k
i
ki
k
mx
k
mx
k
λ∑=
=
0
0
10
1
:ˆ
k
i
ik x
k
m
3 Compute and as function of kσ σ
4 Find k for which
[ ] ϕσσσ σσ =≤≤
2
ˆ
2
k
2
k
ˆ-0Prob n
5 Run k-k0 simulations

231. 232
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue – 11)
Monte-Carlo Procedure
Choose the Confidence Level φ = 95% that gives the
corresponding nσ=1.96.
nσ φ
1.000 0.6827
1.645 0.9000
1.960 0.9500
2.576 0.9900
1
The kurtosis λ = 32
3 Find k for which ϕσ
λ
σσ
σ
σ =












−
≤≤

2
kˆ
22
k
2 1
ˆ-0Prob
k
n
4 Run k>800 simulations
Example:
Assume a gaussian distribution λ = 3
95.0
2
96.1ˆ-0Prob
2
kˆ
22
k
2
=












≤≤

σ
σσσ
k
Assume also that we require also that with probability φ = 95 %22
k
2
1.0ˆ- σσσ ≤
1.0
2
96.1 =
k
800≈k

232. 233
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 12)
Kurtosis of random variable xi
Kurtosis
Kurtosis (from the Greek word κυρτός, kyrtos or kurtos, meaning bulging) is a measure
of the "peakedness" of the probability distribution of a real-valued random variable.
Higher kurtosis means more of the variance is due to infrequent extreme deviations, as
opposed to frequent modestly-sized deviations.
1905 Pearson defines Kurtosis,
as a measure of departure from normality in a paper published in
Biometrika. λ=3 for the normal distribution and the terms
‘leptokurtic’ (λ>3), mesokurtic (λ=3), platikurtic (λ<3) are
introduced.
( ){ } ( ){ }[ ]224
/: mxEmxE ii −−=λ
( ){ }
( ){ }[ ]22
4
:
mxE
mxE
i
i
−
−
=λ
Karl Pearson
(1857 –1936)
A leptokurtic distribution has a more acute "peak" around the mean (that is,
a higher probability than a normally distributed variable of values near the
mean) and "fat tails" (that is, a higher probability than a normally distributed
variable of extreme values).
A platykurtic distribution has a smaller "peak" around the mean (that is, a lower
probability than a normally distributed variable of values near the mean) and
"thin tails" (that is, a lower probability than a normally distributed variable of
extreme values).

233. 234
Hyperbolic-Secant
25






x
2
sech
2
1 π
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 13)
Distribution Graphical
Representation
Functional
Representation
Kurtosis
λ
Excess
Kurtosis
λ-3
Normal
( )
σπ
σ
µ
2
2
exp 2
2





 −
−
x
3 0
Laplace 






 −
−
b
x
b
µ
exp
2
1
6 3
Uniform
bxorxa
bxa
ab
>>
≤≤
−
0
1
1.8 -1.2
Wigner
Rx
RxxR
R
>
≤−
0
2 22
2
π -1.02

234. 235
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable (continue - 14)
Skewness of random variable xi
Skewness
( ){ }
( ){ }[ ] 2/32
3
:
mxE
mxE
i
i
−
−
=γ Karl Pearson
(1857 –1936)
Negative skew: The left tail is longer; the mass of the distribution is concentrated on
the right of the figure. The distribution is said to be left-skewed.
1
Positive skew: The right tail is longer; the mass of the distribution is concentrated
on the left of the figure. The distribution is said to be right-skewed.
2
More data in the left tail than
it would be expected in a
normal distribution
More data in the righttail than
it would be expected in a
normal distribution
Karl Pearson suggested two simpler calculations as a measure of skewness:
• (mean - mode) / standard deviation
• 3 (mean - median) / standard deviation

235. 236
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable using a
Recursive Filter (Unknown Statistics)
We found that using k measurements the estimated mean and variance are given in
batch form by:
∑=
=
k
i
ik x
k
x
1
1
:ˆ
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to estimate the sample mean, ,
and the variance pk, by a Recursive Filter
kxˆ
The k+1 measurement will give:
( )1
1
1
1
ˆ
1
1
1
1
ˆ +
+
=
+ +
+
=
+
= ∑ kk
k
i
ik xxk
k
x
k
x
( )kkkk xx
k
xx ˆ
1
1
ˆˆ 11 −
+
+= ++
Therefore the Recursive Filter form for the
k+1 measurement will be:
( )∑=
−
−
=
k
i
kik xx
k
p
1
2
ˆ
1
1
:
( )∑
+
=
++ −=
1
1
2
11
ˆ
1 k
i
kik xx
k
p

236. 237
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable using a
Recursive Filter (Unknown Statistics) (continue – 1)
We found that using k+1 measurements the estimated variance is given in
batch form by:
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to estimate the sample mean, ,
and the variance pk, by a Recursive Filter
kxˆ
( ) 


 +
−−
+
+= ++ kkkkk p
k
k
xx
k
pp
1
ˆ
1
1 2
11
( )
( )
( )
( )
( )
( ) ( ) ( )
( )
( ) ( )2
1
2
12
1
0
1
1
2
1
1
1
2
1
1
2
1
1
1
2
11
ˆ
1
11
1ˆ
1
1
ˆˆˆ
1
2
ˆˆ
1
1
ˆ
ˆ
1
ˆ
1
kkkkk
kk
k
i
kikkkk
pk
k
i
ki
k
i
kk
ki
k
i
kik
xx
k
p
k
xx
kk
k
xxxxxx
kk
xxxx
k
k
xx
xx
k
xx
k
p
k
−
+
+





−=−
+
+
+










−+−−
+
−












−+−=






+
−
−−=−=
++
+
=
++
−
=
+
=
+
+
=
++
∑∑
∑∑

( )kkkk xx
k
xx ˆ
1
1
ˆˆ 11 −
+
+= ++

237. 238
SOLO Review of Probability
Estimation of the Mean and Variance of a Random Variable using a
Recursive Filter (Unknown Statistics) (continue – 2)
A random variable, x, may take on any values in the range - ∞ to + ∞.
Based on a sample of k values, xi, i = 1,2,…,k, we wish to estimate the sample mean, ,
and the variance pk, by a Recursive Filter
kxˆ
( ) 


 +
−−
+
+= ++ kkkkk p
k
k
xx
k
pp
1
ˆ
1
1 2
11
( )kkkk xx
k
xx ˆ
1
1
ˆˆ 11 −
+
+= ++
( ) ( ) ( )kkkk xxkxx ˆˆ1ˆ 11 −+=− ++
( )( ) 



−−++= ++ kkkkk p
k
xxkpp
1
ˆˆ1
2
11

238. 239
SOLO Review of Probability
Estimate the value of a constant x, given discrete measurements of x corrupted by an
uncorrelated gaussian noise sequence with zero mean and variance r0.
The scalar equations describing this situation are:
kk xx =+1
kkk vxz +=
System
Measurement ( )0,0~ rNvk
The Discrete Kalman Filter is given by:
( ) ( )+=−+ kk xx ˆˆ 1
( ) ( ) ( ) ( )[ ] ( )[ ]−−+−−+−=+ ++
−
++++
+
11
1
01111
ˆˆˆ
1
kk
K
kkkk xzrppxx
k
  
 
0
1 kkk
I
kk wxx Γ+Φ=+
 kk
I
kk vxHz +=
( ) ( )[ ] ( )[ ]{ } 
( )
( )+=ΓΓ+Φ+Φ=−−−−=− +++++ k
T
I
T
kk
I
k
T
kkkkk pQpxxxxEp

0
11111
ˆˆ
( ) ( )[ ] ( )[ ]{ }
( ) ( )  
( )  
( )
( ) ( ) ( )
( ) 0
0
11
1
0111111
11111
1
1
ˆˆ
rp
pr
pHrHpHHpp
xxxxEp
k
k
pp
k
I
k
K
T
I
kk
I
k
T
I
kkk
T
kkkkk
kk
k
++
+
=−








+−−−−=
−+−+=+
+=−
++
−
++++++
+++++
+
+
  
General Form
with Known Statistics Moments Using a Discrete Recursive Filter
Estimation of the Mean and Variance of a Random Variable

239. 240
SOLO Review of Probability
Estimate the value of a constant x, given discrete measurements of x corrupted by an
uncorrelated gaussian noise sequence with zero mean and variance r0.
We found that the Discrete Kalman Filter is given by:
( ) ( ) ( )[ ]+−++=+ +++ kkkkk xzKxx ˆˆˆ 111
( ) ( )
( )
( )
( )
0
0
0
1
1
r
p
p
rp
pr
p
k
k
k
k
k
+
+
+
=
++
+
=++
( )
0
0
0
1
1
r
p
p
p
+
=+ ( ) ( )
( )
0
1
1
2
1
r
p
p
p
+
+
+
=+ ( )
k
r
p
p
pk
0
0
0
1+
=+
( )
( ) 0
1
rp
p
K
k
k
k
++
+
=+
( )
( ) 0
1
rp
p
K
k
k
k
++
+
=+( ) ( )
( )
( )[ ]+−
++
++=+ ++ kkkk xz
k
r
p
r
p
xx ˆ
11
ˆˆ 1
0
0
0
0
1
0=k
1=k
0
0
0
2
1
r
p
p
+
=
( )11
1
1
0
0
0
0
0
0
0
0
0
0
0
++
=
+
+
+
=
k
r
p
r
p
r
k
r
p
p
k
r
p
p
with Known Statistics Moments Using a Discrete Recursive Filter (continue – 1)
Estimation of the Mean and Variance of a Random Variable

240. 241
SOLO Review of Probability
Estimate the value of a constant x, given continuous measurements of x corrupted by an
uncorrelated gaussian noise sequence with zero mean and variance r0.
The scalar equations describing this situation are:
0=x
vxz +=
System
Measurement ( )rNv ,0~
The Continuous Kalman Filter is given by:
( )  ( ) ( ) ( ) ( )[ ] ( ) 00ˆ&ˆˆˆ
1
1
0
=−





+=
+
−
xtxtzrHtptxAtx
kK
I


 
00
wxAx Γ+=
 vxHz
I
+=
( ) ( ) ( )[ ] ( ) ( )[ ]{ }T
txtxtxtxEtp −−= ˆˆ:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 12
1
1
000
−−
−=−++= rtptptHrtHtptGQtGtAtptptAtp TT
I
TT


General Form
with Known Statistics Moments Using a Continuous Recursive Filter
Estimation of the Mean and Variance of a Random Variable
( ) ( ) ( ) 0
12
0& ptprtptp ==−= −
or:
∫∫ −=
tp
p
dt
rp
pd
0
2
0
1 ( )
t
r
p
p
tp
0
0
1+
=
( )
t
r
p
r
p
rtpK
0
0
1
1+
== −
( ) ( )[ ]txz
t
r
p
r
p
tx ˆ
1
ˆ
0
0
−
+
=

241. 242
SOLO Review of Probability
Monte Carlo approximation
Monte Carlo runs , generate a set of samples that approximate the filtering distribution .
So, with P samples, expectations with respect to the filtering distribution are approximated by
( )xp
( ) ( ) ( )
( )∑∫ =
≈
P
L
L
xf
P
dxxpxf
1
1
and , in the usual way for Monte Carlo, can give all the moments etc. of the distribution
up to some degree of approximation.
{ } ( ) ( )
∑∫ =
≈==
P
L
L
x
P
dxxpxxE
1
1
1
µ
( ){ } ( ) ( ) ( )
( )∑∫ =
−≈−=−=
P
L
nLnn
n x
P
dxxpxxE
1
111
1
µµµµ


242. 243
SOLO Review of Probability
Types of Estimation
t t+τ
t
available measurement data
t
available measurement data
available measurement data
Filtering
t+τ
τ > 0
τ > 0
Use all the measurement data
to the present time t to estimate.
Smoothing
Use all the measurement data
to a future time t+τ to estimate
at present time t..
Prediction
Use all the measurement data
to the present time t to predict
the outcome at a future time t + τ.

243. 244
SOLO Review of Probability
Conditional Expectations and Their Smoothing Property
The Conditional Expectation is defined as: { } ( )∫
+∞
∞−
= dxyxpxyxE yx || |
Similarly, for a function of x and y, g (x,y), the Conditional Expectation is defined as:
( ){ } ( ) ( )∫
+∞
∞−
= dxyxpyxgyyxgE yx |,|, |
Smoothing property of the Expectation states that the Expected value of the Conditional
Expectation is equal to the Unconditional Expected Value
{ }{ } ( ) ( )
( ) ( )
( )
( ) { }xEdxxpx
dxdyyxpx
dxdyypyxpx
dyypdxyxpxyxEE
x
yx
yyx
yyx
==






=






=






=
∫
∫ ∫
∫ ∫
∫ ∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
+∞
∞−
+∞
∞−
,
|
||
,
|
|
{ }{ } { }xEyxEE =|
This relation is also called the Law of Iterated Expectation, summarized as:

244. 245
SOLO Review of Probability
Gaussian Mixture Equations
A mixture is a p.d.f. given by a weighted sum of p.d.f.s with the weighths summing up
to unity:
( ) ( )∑=
=
n
j
jjj Pxxpxp
1
,;N
A Gaussian Mixture is a p.d.f. consisting of a weighted sum of Gaussian densities
where:
1
1
=∑=
n
j
jp
( ){ }jjj PxxA ,~: N=
Denote by Aj the event that x is Gaussian distributed with mean and covariance Pjjx
with Aj , j=1,…,n, mutually exclusive and exhaustive:
and S
1A 2A nA
{ } jj pAP =:
jiOAAandSAAA jin ≠∀/=∩=∪∪∪ 21
( ) ( ) ( ) ( )∑∑ ==
==
n
j
jj
n
j
jjj AxpAPPxxpxp
11
|,;NTherefore:

245. 246
SOLO Review of Probability
Gaussian Mixture Equations (continue – 1)
A Gaussian Mixture is a p.d.f. consisting of a weighted sum of Gaussian densities
( ) ( ) ( ) ( )∑∑ ==
==
n
j
jj
n
j
jjj AxpAPPxxpxp
11
|,;N
The mean of such a mixture is:
{ } ( ) ( ){ } ∑∑ ==
====
n
j
jj
n
j
jjj xpPxxEpxpxEx
11
,;N
The covariance of the mixture is:
( ) ( ){ } ( ) ( ){ }
( ) ( ){ }
( )( ){ } ( ){ }( )
( ) ( ){ } ( )( )∑∑
∑∑
∑
∑
==
==
=
=
−−+−−+
−−+−−=
−+−−+−=
−−=−−
n
j
j
T
jj
n
j
jj
T
jj
n
j
j
T
jjj
n
j
jj
T
jj
n
j
jj
T
jjjj
n
j
jj
TT
pxxxxpAxxExx
pxxAxxEpAxxxxE
pAxxxxxxxxE
pAxxxxExxxxE
11
0
1
0
1
1
1
  
  

246. 247
SOLO Review of Probability
Gaussian Mixture Equations (continue – 2)
The covariance of the mixture is:
( ) ( ){ } ( )( ){ } ( )( ) PpPpxxxxpAxxxxExxxxE
n
j
jj
n
j
j
T
jj
n
j
jj
T
jj
T ~
111
+=−−+−−=−− ∑∑∑ ===
where:
( )( )∑=
−−=
n
j
j
T
jj pxxxxP
1
:
~
Is the spread of the mean term.
T
n
j
j
T
jj
n
j
j
TT
x
n
j
jj
x
n
j
j
T
j
n
j
j
T
jj
xxpxx
pxxxpxpxxpxxP
T
−=
+−−=
∑
∑∑∑∑
=
====
1
1
1111
:
~

( ) ( ){ } T
n
j
j
T
jj
n
j
jj
T
xxpxxpPxxxxE −+=−− ∑∑ == 11
Note: Since we developed only first and second moments of the mixture, those relations
will still be correct even if the random variables in the mixture are not Gaussian.

247. 248
SOLO
Linear Gaussian Systems
A Linear Combination of Independent Gaussian random vectors is also a
Gaussian random vector mmm XaXaXaS +++= 2211:
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
( ) ( )



+++++++−=




+−



+−



+−=
ΦΦ⋅Φ==Φ ∫ ∫
+∞
∞−
+∞
∞−
mmmm
mmmm
YYYm
YpYp
mYYmS
aaajaaa
ajaajaaja
YdYdYYpSj m
mmYY
mm
µµµωσσσω
µωσωµωσωµωσω
ωωωωω



  



2211
222
2
2
2
2
1
2
1
2
222
22
2
2
2
2
2
11
2
1
2
1
2
11,,
2
1
exp
2
1
exp
2
1
exp
2
1
exp
,,exp 21
11
1
( ) ( )





 −
−= 2
2
2
exp
2
1
,;
i
ii
i
iiiX
X
Xp i
σ
µ
σπ
σµ ( ) ( ) ( ) 



+−==Φ ∫
+∞
∞−
iiiiXiX jXdXpXj ii
µωσωωω
22
2
1
expexp:
Moment-
Generating
Function
Gaussian
distribution
Define
Proof:
( ) ( )iX
ii
i
X
i
iYiii Xp
aa
Y
p
a
YpXaY iii
11
: =





=→=
( ) ( ) ( ) ( )
( )
( ) 





+−=Φ===Φ ∫∫
+∞
∞−
+∞
∞−
iiiiiiX
asign
asign
ii
i
iX
iiiiYiY ajaXaXda
a
Xp
XajYdYpYj i
i
ii
µωσωωωω
222
2
1
expexpexp:
1
1
Review of Probability

248. 249
SOLO
Linear Gaussian Systems
A Linear Combination of Independent Gaussian random vectors is also a
Gaussian random vector mmm XaXaXaS +++= 2211:
Therefore the Linear Combination of Independent Gaussian Random Variables is a
Gaussian Random Variable with
mmS
mmS
aaa
aaa
m
m
µµµµ
σσσσ
+++=
+++=


2211
222
2
2
2
2
1
2
1
2
Therefore the Sm probability distribution is:
( ) ( )







 −
−= 2
2
2
exp
2
1
,;
m
m
m
mm
S
S
S
SSm
x
Sp
σ
µ
σπ
σµ
Proof (continue – 1):
( ) ( ) ( )





+++++++−=Φ mmmmS aaajaaam
µµµωσσσωω  2211
222
2
2
2
2
1
2
1
2
2
1
exp
We found:
Review of Probability

249. 250
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems
kkkk
kkkkkkk
vxHz
wuGxx
+=
Γ++Φ= −−−−−− 111111
wk-1 and vk, white noises, zero mean, Gaussian, independent
( ) ( ) ( ){ } ( ) ( ){ } ( )kPkekeEkxEkxke x
T
xxx =−= &:
( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
www kQlekeEkwEkwke ,
0
&: δ=−=

( ) ( ) ( ){ } ( ) ( ){ } ( ) lk
T
vvv kRlekeEkvEkvke ,
0
&: δ=−=

( ) ( ){ } { }0=lekeE
T
vw



=
≠
=
lk
lk
lk
1
0
,δ
( ) ( )Qwwpw ,0;N=
( ) ( )Rvvpv ,0;N=
( )
( ) 





−= −
wQw
Q
wp T
nw
1
2/12/
2
1
exp
2
1
π
( )
( ) 





−= −
vRv
R
vp T
pv
1
2/12/
2
1
exp
2
1
π
A Linear Gaussian Markov Systems is defined as
( ) ( )0|0000 ,;0
Pxxxp ttx == = N
( )
( )
( ) ( )



−−−= =
−
== 00
1
0|0002/1
0|0
2/0
2
1
exp
2
1
0
xxPxx
P
xp t
T
tntx
π

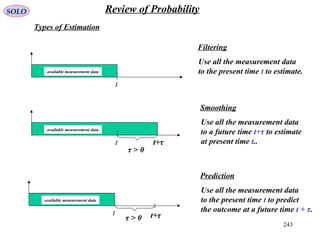
250. 251
Recursive Bayesian EstimationSOLO
Linear Gaussian Markov Systems (continue – 2)
111111 −−−−−− Γ++Φ= kkkkkkk wuGxx
Prediction phase (before zk measurement)
{ } { } { }  
0
1:111111:1111:11| |||:ˆ −−−−−−−−−− Γ++Φ== kkkkkkkkkkkk ZwEuGZxEZxEx
or 111|111|
ˆˆ −−−−−− +Φ= kkkkkkk uGxx
The expectation is
{ }[ ] { }[ ]{ }
( )[ ] ( )[ ]{ }1:1111|111111|111
1:11|1|1|
|ˆˆ
|ˆˆ:
−−−−−−−−−−−−−
−−−−
Γ+−ΦΓ+−Φ=
−−=
k
T
kkkkkkkkkkkk
k
T
kkkkkkkk
ZwxxwxxE
ZxExxExEP
( ) ( ){ } ( ){ }
( ){ } { } T
k
Q
T
kkk
T
k
T
kkkkk
T
k
T
kkkkk
T
k
P
T
kkkkkkk
wwExxwE
wxxExxxxE
kk
11111
0
1|1111
1
0
11|11111|111|111
ˆ
ˆˆˆ
1|1
−−−−−−−−−−
−−−−−−−−−−−−−−
ΓΓ+Φ−Γ+
Γ−Φ+Φ−−Φ=
−−
  
    
T
kk
T
kkkkkk QPP 1111|111| −−−−−−− ΓΓ+ΦΦ=
{ } ( )1|1|1:1 ,ˆ;| −−− = kkkkkkk PxxZxP N
Since is a Linear Combination of Independent
Gaussian Random Variables:
111111 −−−−−− Γ++Φ= kkkkkkk wuGxx
Table of Content

251. 252
Random VariablesSOLO
Random Variable:
A variable x determined by the outcome Ω of a random experiment.
( )Ω= xx
Random Process or Stochastic Process:
A function of time x determined by the outcome Ω of a random experiment.
( ) ( )Ω= ,txtx
1
Ω
2
Ω
3Ω
4Ω
x
t
This is a family or an ensemble of
functions of time, in general different
for each outcome Ω.
Mean or Ensemble Average of the Random Process: ( ) ( )[ ] ( ) ( )∫
+∞
∞−
=Ω= ξξξ dptxEtx tx
,:
Autocorrelation of the Random Process: ( ) ( ) ( )[ ] ( ) ( ) ( )∫ ∫
+∞
∞−
+∞
∞−
=ΩΩ= ηξξξη ddptxtxEttR txtx 21 ,2121
,,:,
Autocovariance of the Random Process: ( ) ( ) ( )[ ] ( ) ( )[ ]{ }221121 ,,:, txtxtxtxEttC −Ω−Ω=
( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( )2121212121 ,,,, txtxttRtxtxtxtxEttC −=−ΩΩ=

252. 253
Random VariablesSOLO
Stationarity of a Random Process
1. Wide Sense Stationarity of a Random Process:
• Mean Average of the Random Process is time invariant:
( ) ( )[ ] ( ) ( ) .,: constxdptxEtx tx
===Ω= ∫
+∞
∞−
ξξξ
• Autocorrelation of the Random Process is of the form: ( ) ( ) ( )τ
τ
RttRttR
tt 21:
2121
,
−=
=−=
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )12,2121 ,,,:, 21
ttRddptxtxEttR txtx === ∫ ∫
+∞
∞−
+∞
∞−
ηξξξηωωsince:
We have: ( ) ( )ττ −= RR
Power Spectrum or Power Spectral Density of a Stationary Random Process:
( ) ( ) ( )∫
+∞
∞−
−= ττωτω djRS exp:
2. Strict Sense Stationarity of a Random Process:
All probability density functions are time invariant: ( ) ( ) ( ) .,,
constptp xtx
== ωωω
Ergodicity:
( ) ( ) ( )[ ]Ω==Ω=Ω ∫
+
−∞→
,,
2
1
:, lim txExdttx
T
tx
Ergodicity
T
TT
A Stationary Random Process for which Time Average = Assembly Average

253. 254
Random VariablesSOLO
Time Autocorrelation:
Ergodicity:
( ) ( ) ( ) ( ) ( )∫
+
−∞→
Ω+Ω=Ω+Ω=
T
TT
dttxtx
T
txtxR ,,
2
1
:,, lim τττ
For a Ergodic Random Process define
Finite Signal Energy Assumption: ( ) ( ) ( ) ∞<Ω=Ω= ∫
+
−∞→
T
TT
dttx
T
txR ,
2
1
,0 22
lim
Define: ( )
( )


 ≤≤−Ω
=Ω
otherwise
TtTtx
txT
0
,
:, ( ) ( ) ( )∫
+∞
∞−
Ω+Ω= dttxtx
T
R TTT
,,
2
1
: ττ
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )∫∫∫
∫∫∫
−−
−
−
+∞
−
−
−
−
∞−
Ω+Ω−Ω+Ω=Ω+Ω=
Ω+Ω+Ω+Ω++Ω=
T
T
TT
T
T
TT
T
T
TT
T
TT
T
T
TT
T
TTT
dttxtx
T
dttxtx
T
dttxtx
T
dttxtx
T
dttxtx
T
dttxtx
T
R
τ
τ
τ
τ
τττ
ττωττ
,,
2
1
,,
2
1
,,
2
1
,,
2
1
,,
2
1
,,
2
1
00

Let compute:
( ) ( ) ( ) ( ) ( )∫∫ −∞→−∞→∞→
Ω+Ω−Ω+Ω=
T
T
TT
T
T
T
TT
T
T
T
dttxtx
T
dttxtx
T
R
τ
τττ ,,
2
1
,,
2
1
limlimlim
( ) ( ) ( )ττ Rdttxtx
T
T
T
TT
T
=Ω+Ω∫−∞→
,,
2
1
lim
( ) ( ) ( ) ( )[ ] 0,,
2
1
,,
2
1
suplimlim →








Ω+Ω≤Ω+Ω
≤≤−∞→−∞→
∫ τττ
ττ
txtx
T
dttxtx
T
TT
TtTT
T
T
TT
T
therefore: ( ) ( )ττ RRT
T
=
→∞
lim
( ) ( ) ( )[ ]Ω==Ω=Ω ∫
+
−∞→
,,
2
1
:, lim txExdttx
T
tx
Ergodicity
T
TT
T− T+
( )txT
t

254. 255
Random VariablesSOLO
Ergodicity (continue - 1):
( ) ( ) ( ) ( ) ( )
( ) ( )[ ] ( ) ( )( )[ ]
( ) ( ) ( ) ( )( )
( ) ( ) ( ) ( ) [ ]TTTT
TT
TT
TTT
XX
T
dvvjvxdttjtx
T
dtjtxdttjtx
T
ddttjtxtjtx
T
dttxtxdj
T
djR
*
2
1
exp,exp,
2
1
exp,exp,
2
1
exp,exp,
2
1
,,exp
2
1
exp
=−ΩΩ=
+−Ω+Ω=
+−Ω+Ω=
Ω+Ω−=−
∫∫
∫∫
∫ ∫
∫ ∫∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
+∞
∞−
+∞
∞−
+∞
∞−
ωω
ττωτω
ττωτω
τττωττωτLet compute:
where: and * means complex-conjugate.( ) ( )∫
+∞
∞−
−Ω= dvvjvxX TT ωexp,:
Define:
( ) ( ) ( ) ( ) ( ) ( )[ ]∫ ∫∫
+∞
∞−
+
−∞→
+∞
∞−∞→∞→ 







Ω+Ω−=








−=








= τττωττωτω ddttxtxE
T
jdjRE
T
XX
ES
T
T
TT
T
T
T
TT
T
,,
2
1
expexp
2
: limlimlim
*
Since the Random Process is Ergodic we can use the Wide Stationarity Assumption:
( ) ( )[ ] ( )ττ RtxtxE TT =Ω+Ω ,,
( ) ( ) ( ) ( ) ( )
( ) ( )∫
∫ ∫∫ ∫
∞+
∞−
+∞
∞−
+
−∞→
+∞
∞−
+
−∞→∞→
−=








−=








−=








=
ττωτ
ττωττττωω
djR
ddt
T
jRddtR
T
j
T
XX
ES
T
TT
T
TT
TT
T
exp
2
1
exp
2
1
exp
2
:
1
*
limlimlim
  

255. 256
Random VariablesSOLO
Ergodicity (continue - 2):
We obtained the Wiener-Khinchine Theorem (Wiener 1930):
( ) ( ) ( )∫
+∞
∞−→∞
−=





= dtjR
T
XX
ES TT
T
τωτω exp
2
:
*
lim
Norbert Wiener
1894 - 1964
Alexander Yakovlevich
Khinchine
1894 - 1959
The Power Spectrum or Power Spectral Density of
a Stationary Random Process S (ω) is the Fourier
Transform of the Autocorrelation Function R (τ).

256. 257
Random VariablesSOLO
White Noise
A (not necessary stationary) Random Process whose Autocorrelation is zero for
any two different times is called white noise in the wide sense.
( ) ( ) ( )[ ] ( ) ( )211
2
2121
,,, ttttxtxEttR −=ΩΩ= δσ
( )1
2
tσ - instantaneous variance
Wide Sense Whiteness
Strict Sense Whiteness
A (not necessary stationary) Random Process in which the outcome for any two
different times is independent is called white noise in the strict sense.
( ) ( ) ( ) ( )2121,
,,21
ttttp txtx
−=Ω δ
A Stationary White Noise Random has the Autocorrelation:
( ) ( ) ( )[ ] ( )τδσττ 2
,, =Ω+Ω= txtxER
Note
In general whiteness requires Strict Sense Whiteness. In practice we have only
moments (typically up to second order) and thus only Wide Sense Whiteness.

257. 258
Random VariablesSOLO
White Noise
A Stationary White Noise Random has the Autocorrelation:
( ) ( ) ( )[ ] ( )τδσττ 2
,, =Ω+Ω= txtxER
The Power Spectral Density is given by performing the Fourier Transform of the
Autocorrelation:
( ) ( ) ( ) ( ) ( ) 22
expexp στωτδστωτω =−=−= ∫∫
+∞
∞−
+∞
∞−
dtjdtjRS
( )ωS
ω
2
σ
We can see that the Power Spectrum Density contains all frequencies at the same
amplitude. This is the reason that is called White Noise.
The Power of the Noise is defined as: ( ) ( ) 2
0 σωτ ==== ∫
+∞
∞−
SdtRP

258. 259
Random VariablesSOLO
Table of Content
Markov Processes
A Markov Process is defined by:
Andrei Andreevich
Markov
1856 - 1922
( ) ( )( ) ( ) ( )( ) 111
,|,,,|, tttxtxptxtxp >∀ΩΩ=≤ΩΩ ττ
i.e. the Random Process, the past up to any time t1 is fully defined
by the process at t1.
Examples of Markov Processes:
1. Continuous Dynamic System
( ) ( )
( ) ( )wuxthtz
vuxtftx
,,,
,,,
=
=
2. Discrete Dynamic System
( ) ( )
( ) ( )kkkkk
kkkkk
wuxthtz
vuxtftx
,,,
,,,
1
1
=
=
+
+
x - state space vector (n x 1)
u - input vector (m x 1)
v - white input noise vector (n x 1)
- measurement vector (p x 1)z
- white measurement noise vector (p x 1)w

259. 260
Random VariablesSOLO
Table of Content
Markov Processes
Examples of Markov Processes:
3. Continuous Linear Dynamic System
( ) ( ) ( )
( ) ( )txCtz
tvtxAtx
=
+=
Using the Fourier Transform we obtain: ( ) ( )
( )
( ) ( ) ( )ωωωωω
ω
VVAIjCZ H
H
=−=
−
  
1
Using the Inverse Fourier Transform we obtain:
( ) ( ) ( )∫
+∞
∞−
= ξξξ dvtHtz ,
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
( )
( ) ( )( )
( )
( ) ( ) ( )∫∫ ∫
∫ ∫∫
∞+
∞−
∞+
∞−
−
∞+
∞−
+∞
∞−
+∞
∞−
+∞
∞−
−=−=






−==
ξξξξξωξωω
π
ωωξξωξω
π
ωωωω
π
ξ
ω
dvtHdvdtj
dtjdjvdtjVtz
tH
egrattion
of
order
change
V
  
  
exp
2
1
expexp
2
1
exp
2
1
int
H
HH

260. 261
Random VariablesSOLO
Table of Content
Markov Processes
Examples of Markov Processes:
3. Continuous Linear Dynamic System
( ) ( ) ( )
( ) ( )txCtz
tvtxAtx
=
+=
The Autocorrelation of the output is:
( ) ( ) ( )∫
+∞
∞−
= ξξξ dvtHtz ,
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )
( ) ( ) ( )[ ] ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )∫∫
∫ ∫∫ ∫
∫∫
∞+
∞−
−=∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
+∞
∞−
+∞
∞−
+=−+−=
−−+−=−+−=






−+−=+=
ζτζζξξτξ
ξξξξδξτξξξξτξξξ
ξξτξξξξττ
ξζ
dHSHdtHStH
ddtHStHddtHvvEtH
dtHvdvtHEtztzER
T
vv
t
T
vv
T
vv
TT
TTT
zz
1
111
212121211211
222111
( ) ( ) ( )[ ] ( )τδττ vv
T
vv StvtvER =+=
( ) ( ) ( ) ( ) ( ) vvvvvvvv SdjSdjRS =−=−= ∫∫
+∞
∞−
+∞
∞−
ττωτδττωτω expexp
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )ωωχχωχζζωζ
χχωζζωζχττζωζζωζτζ
ττωζτζζττωτω
χτζ
ττ
*
expexp
expexpexpexp
expexp
HH vv
T
vv
T
vv
T
vv
T
vv
RR
zzzz
SdjHSdjH
djdjHSHdjdjHSH
djdHSHdjRS
zzzz
=











−=
−=−−−=
−−=−=
∫∫
∫ ∫∫ ∫
∫ ∫∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
=+∞+
∞−
∞+
∞−
+∞
∞−
+∞
∞−
−=+∞
∞−
( ) ( ) ( ) ( ) conjugatecomplexSS vvzz −== ∗
ωωωω *
HH

261. 262
Random VariablesSOLO
Table of Content
Markov Processes
Examples of Markov Processes:
4. Continuous Linear Dynamic System ( ) ( ) ( )∫
+∞
∞−
= ξξξ dvthtz ,
( ) ( ) ( )[ ] ( )τδσττ
2
vvv tvtvER =+= ( ) 2
vvvS σω =
v (t) z (t)
( )
xj
K
H
ωω
ω
/1+
=
( )
x
j
K
H
ωω
ω
/1+
=
The Power Spectral Density of the output is:
( ) ( ) ( ) ( )
( )2
22
*
/1 x
v
vvzz
K
HSHS
ωω
σ
ωωωω
+
==
( )
( )2
22
/1 x
vv
zz
K
S
ωω
σ
ω
+
=
ω
x
ω
22
vv
K σ
2/
22
vv
K σ
The Autocorrelation of the output is:
( ) ( ) ( )
( )
( )
( )
( )∫∫
∫
∞+
∞−
=
∞+
∞−
+∞
∞−
−
−
=
+
=
=
dss
s
K
j
dj
K
djSR
x
v
js
x
v
zzzz
τ
ω
σ
π
ωτω
ωω
σ
π
ωτωω
π
τ
ω
exp
/12
1
exp
/12
1
exp
2
1
2
22
2
22
ωj
xω
R
( )
0
/1
2
22
=
−∫∞→R
s
x
vv
dse
s
K τ
ω
σ
( )
0
/1
2
22
=
−∫∞→R
s
x
vv
dse
s
K τ
ω
σ
xω−
σ
ωσ js +=
0<τ
0>τ
( ) τωσω
ω x
e
K
R vvx
zz
=
=
2
22
τ
2/
22
vvxK σω
( )τω
σω
x
vx
K
−= exp
2
22
( )
( )
( )
( )














>







+
−
−=
−
−
<








−
−
=
−
−
=
∫
∫
→
−→
0
exp
Reexp
2
1
0
exp
Reexp
2
1
222
22
222
222
22
222
τ
ω
τσω
τ
ω
σω
π
τ
ω
τσω
τ
ω
σω
π
ωω
ωω
x
vx
x
vx
x
vx
x
vx
s
sK
sdss
s
K
j
s
sK
sdss
s
K
j
x
x

262. 263
Random VariablesSOLO
Markov Processes
Examples of Markov Processes:
5. Continuous Linear Dynamic System with Time Variable Coefficients
( ) ( ) ( ){ } ( ) ( ) ( ){ }
( ) ( ){ } ( ) ( )21121
&
:&:
tttQteteE
twEtwtetxEtxte
T
ww
wx
−=
−=−=
δ
w (t) x (t)
( )tF
( )tG ∫
x (t)
( ) ( ) ( ) ( ) ( ) ( )twtGtxtFtxtx
td
d
+== 
( ) ( ) ( ) ( ) ( )tetGtetFte wxx +=
( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
dwGttxtttx
0
,, 00
λλλλ
The solutions of the Linear System are:
where:
( ) ( ) ( ) ( ) ( ) ( ) ( )3132210000
,,,&,&,, ttttttItttttFtt
td
d
Φ=ΦΦ=ΦΦ=Φ
( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
wxx deGttettte
0
,, 00 λλλλ
( ){ } ( ) ( ){ } ( ) ( ){ }twEtGtxEtFtxE +=

263. 264
Random VariablesSOLO Markov Processes
Examples of Markov Processes:
5. Continuous Linear Dynamic System with
Time Variable Coefficients (continue – 1)
( ) ( ) ( ){ } ( ) ( ) ( ){ }
( ) ( ){ } ( ) ( )21121
&
:&:
tttQteteE
twEtwtetxEtxte
T
ww
wx
−=
−=−=
δ
w (t) x (t)
( )tF
( )tG ∫
x (t)
( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
dwGttxtttx
0
,, 00 λλλλ ( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
wxx
deGttettte
0
,, 00
λλλλ
( ) ( ){ } ( ) ( ){ } ( )ttRteteEtxVartV x
T
xxx ,: ===( ) ( ) ( ){ }2121 :, teteEttR
T
xxx =
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ){ }
( )
( ) ( ) ( ) ( ){ } ( ) ( )
( ) ( ) ( ) ( ){ } ( ) ( ) ( ) ( ) ( ){ }
( ) ( )
( ) ( )∫∫∫
∫
∫∫
ΦΦ+Φ








Φ+
ΦΦ+ΦΦ=
















Φ+Φ








Φ+Φ=
−
1
0
2
0
211
1
0
2
0
00
2
0
1
0
222222111102101111
2222200102
,
0001
222220021111100121
1,,,,
,,,,
,,,,,
t
t
t
t
TT
Q
T
ww
T
t
t
T
t
t
TTTT
ttV
T
xx
T
t
t
t
t
x
ddtGeeEGtttdtxwEGt
dtGwtxEttttteteEtt
dwGttxttdwGttxttEttR
x
λλλλλλλλλλλλ
λλλλ
λλλλλλλλ
λλδλ
  
  
( ) ( ){ } ( ) ( ){ }
( ) ( ) ( ) ( ){ }
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
∫∫∫
=
−
ΦΦ=ΦΦ
≤≤←==
21
0
1
0
2
0
211
,min
2122221111
212102001
,,,,
,,0
ttt
t
TT
t
t
t
t
TT
Q
T
ww
TT
dtGQGtddtGeeEGt
tttwtxEtxwE
λλλλλλλλλλλλλλ
λλλλ
λλδλ
  

264. 265
Random VariablesSOLO Markov Processes
Examples of Markov Processes:
5. Continuous Linear Dynamic System with
Time Variable Coefficients (continue – 2)
( ) ( ) ( ){ } ( ) ( ) ( ){ }
( ) ( ){ } ( ) ( )21121
&
:&:
tttQteteE
twEtwtetxEtxte
T
ww
wx
−=
−=−=
δ
w (t) x (t)
( )tF
( )tG ∫
x (t)
( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
dwGttxtttx
0
,, 00 λλλλ ( ) ( ) ( ) ( ) ( ) ( )∫Φ+Φ=
t
t
wxx
deGttettte
0
,, 00
λλλλ
( ) ( ){ } ( ) ( ){ } ( )ttRteteEtxVartV x
T
xxx ,: ===( ) ( ) ( ){ }2121 :, teteEttR
T
xxx =
( ) ( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
∫
=
ΦΦ+ΦΦ==
21
0
,min
0200012121 ,,,,,,
ttt
t
TTT
x
T
x dtGQGtttttVtttxtxEttR λλλλλλ
( ) ( ) ( ){ } ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )∫ ΦΦ+ΦΦ===
t
t
TTT
xx
T
x dtGQGtttttVttttRtxtxEtV
0
,,,,,, 0000 λλλλλλ

265. 266
Random VariablesSOLO Markov Processes
Examples of Markov Processes:
6. Discrete Linear Dynamic System with Variable Coefficients
( ) ( ) ( ) ( ) ( )kwkkxkkx Γ+Φ=+1
( ) ( ) ( ){ }
( ) ( ){ } ( )lkQlekeE
kwEkwke
w
T
ww
w
−=
−=
δ
:
( ) ( ) ( ){ }
( ) ( ){ } ( )kXkekeE
kxEkxke
T
xx
x
=
−=:
( ) ( ){ } lkkekeE
T
wx ,0 ∀=
( ){ } ( ) ( ){ } ( ) ( ){ }kwEkkxEkkxE Γ+Φ=+1
( ) ( ) ( ) ( ) ( )kekkekke wxx Γ+Φ=+1
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( ) ( ) ( )kekkekkkekkkekkekke wwx
kk
wxx 1111112
,2
+Γ+Γ+Φ+Φ+Φ=+Γ+++Φ=+
+Φ
  
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )∑
−+
=
+Φ
Γ++Φ+Φ+Φ−+Φ=+
1
,
1,11
lk
kn
wx
klk
x nennlkkekklklke
  

where we defined ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )kmknnmIkkkklkklk ,,,&,11:, Φ=ΦΦ=ΦΦ+Φ−+Φ=+Φ 
Hence ( ) ( ) ( ) ( ) ( ) ( )∑
−+
=
Γ++Φ++Φ=+
1
1,,
lk
kn
wxx nennlkkeklklke
( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }∑
−+
=
Γ++Φ++Φ=+
1
1,,
lk
kn
T
xw
T
xx
T
xx keneEnnlkkekeEklkkelkeE

266. 267
Random VariablesSOLO Markov Processes
Examples of Markov Processes:
6. Discrete Linear Dynamic System with Variable Coefficients (continue – 1)
( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }∑
−+
=
Γ++Φ++Φ=+
1
1,,
lk
kn
T
xw
T
xx
T
xx keneEnnlkkekeEklkkelkeE
( ) ( ) ( ) ( ) ( ) ( )∑
−+
=
Γ++Φ++Φ=+
1
1,,
lk
kn
wxx nennlkkeklklke
( ) ( ) ( ) ( ) ( ) ( )∑
−
−=
Γ+Φ+−−Φ=
1
1,,
k
lkm
wxx memmklkelkkke



=
−
→
,2,1l
lk
k
( ) ( ){ } ( ) ( ){ } ( ) ( ) ( ){ }
( )
( ) ( )∑
−
−=
−
+ΦΓ+−Φ−=
1
1,,
k
lkm
TT
mnQ
T
ww
TT
xw
T
xw mkmmeneElkklkeneEkeneE
w
  
δ
[ ]
[ ]





=
−−∈
−+∈
,2,1
1,
1,
l
klkm
lkkn
( ) ( ){ }
( ) 0
0
=−
=−
nmQ
lkeneE
w
T
xw
δ
( ) ( ){ } 0=keneE
T
xw
( ) ( ){ } ( ) ( ) ( ){ }kekeEklkkelkeE
T
xx
T
xx ,+Φ=+

267. 268
Random VariablesSOLO Markov Processes
Examples of Markov Processes:
6. Discrete Linear Dynamic System with Variable Coefficients (continue – 2)
( ) ( ){ } ( ) ( ){ } ( ) ( ) ( ){ } ( ) ( )∑
−+
=
++ΦΓ++Φ=+
1
1,,
lk
kn
TTT
wx
TT
xx
T
xx nlknnekeEklkkekeElkekeE
( ) ( ) ( ) ( ) ( ) ( )∑
−+
=
Γ++Φ++Φ=+
1
1,,
lk
kn
wxx nennlkkeklklke
( ) ( ) ( ) ( ) ( ) ( )∑
−
−=
Γ+Φ+−−Φ=
1
1,,
k
lkm
wxx memmklkelkkke



=
−
→
,2,1l
lk
k
( ) ( ){ } ( ) ( ) ( ){ } ( ) ( ) ( ) ( ){ }
( )
∑
−
−=
−
Γ+Φ+−−Φ=
1
1,,
k
lkm
nmQ
T
ww
T
w
T
x
T
wx
w
nemeEmmknelkeElkknekeE
  
δ
[ ]
[ ]





=
−−∈
−+∈
,2,1
1,
1,
l
klkm
lkkn
( ) ( ){ }
( ) 0
0
=−
=−
mnQ
nelkeE
w
T
wx
δ
( ) ( ){ } 0=nekeE
T
wx
( ) ( ){ } ( ) ( ){ } ( )klkkekeElkekeE TT
xx
T
xx ,+Φ=+
Table of Content

268. 269
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
q.e.d.
( ) ( )ABtraceBAtrace =1
Proof:
( ) ∑ ∑= =








=
n
i
n
j
jiij baBAtrace
1 1
( ) ( )BAtracebaabABtrace
n
i
n
j
jiij
n
j
n
i
ijji ==





= ∑∑∑ ∑ = == = 1 11 1
( ) ( )
( )
( )
( )
( ) ( )
( )
( )ABtraceBAtraceBAtraceABtraceABtraceBAtrace TTTT
111
=≠===2
Proof:
( ) ( ) ( )ABtraceBAtracebabaBAtrace
n
i
n
j
jiij
n
i
n
j
ijij
T
==







≠







= ∑ ∑∑ ∑ = == = 1 11 1
( ) ( )T
n
j
n
i
ijij
T
BAtraceabABtrace =





= ∑ ∑= =1 1
q.e.d.

269. 270
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
3
Proof:
q.e.d.
( ) ( ) ( )∑=
−
==
n
i
i APAPtraceAtrace
1
1
λ
where P is the eigenvector matrix of A related to the eigenvalue matrix Λ of A by










=Λ=
n
PPPA
λ
λ



0
01
( )
( )
( ) ( )AtraceAPPtracePAPtrace == −− 1
1
1










=Λ=
n
PPPA
λ
λ



0
01










=Λ=→ −
n
PAP
λ
λ



0
01
1
( ) ( ) ∑=
−
=Λ=→
n
i
itracePAPtace
1
1
λ

270. 271
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
Proof:
q.e.d.
Definition
4
( )AtraceA
ee =det
( )AtraceA
eeePe
P
PePPePe
n
i
i
======
∑=ΛΛΛ−Λ− 1
detdetdet
det
1
detdetdetdetdet 11
λ
If aij are the coefficients of the matrix Anxn and z is a scalar function of aij, i.e.:
( ) njiazz ij ,,1, ==
then is the matrix nxn whose coefficients i,j areA
z
∂
∂
nji
a
z
A
z
ijij
,,1,: =
∂
∂
=





∂
∂
(see Gelb “Applied Optimal Estimation”, pg.23)

271. 272
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
Proof:
q.e.d.
5
( ) ( ) ( )
A
Atrace
I
A
Atrace T
n
∂
∂
==
∂
∂ 1
( )



=
≠
==
∂
∂
=





∂
∂
∑= ji
ji
a
aA
Atrace
ij
n
i
ii
ijij
1
0
1
δ
6
( ) ( ) ( ) ( ) nmmnTTT
RBRCCBBC
A
BCAtrace
A
ABCtrace ××
∈∈==
∂
∂
=
∂
∂ 1
Proof:
( ) ( ) ( )[ ]ij
T
ji
m
p
pijp
ik
jl
n
l
m
p
n
k
klpklp
ijij
BCBCbcabc
aA
ABCtrace
===
∂
∂
=





∂
∂
∑∑∑∑ =
=
=
= = = 11 1 1
q.e.d.
7 If A, B, C ∈ Rnxn
,i.e. square matrices, then
( ) ( ) ( ) ( ) ( ) ( ) TTT
CBBC
A
BCAtrace
A
CABtrace
A
ABCtrace
==
∂
∂
=
∂
∂
=
∂
∂ 11

272. 273
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
Proof:
q.e.d.
8 ( ) ( ) ( ) ( ) ( )( )( )
nmmn
TTT
RBRCBC
A
ABCtrace
A
BCAtrace
A
ABCtrace ××
∈∈=
∂
∂
=
∂
∂
=
∂
∂ 721
9
( )( ) ( )( ) ( )( )
BC
A
BCAtrace
A
CABtrace
A
ABCtrace TTT 811
=
∂
∂
=
∂
∂
=
∂
∂
If A, B, C ∈ Rnxn
,i.e. square matrices, then
1
0
( ) T
A
A
Atrace
2
2
=
∂
∂
( ) ( ) ( )ij
T
jiji
n
l
n
m
mllm
ijijij
Aaaaa
aa
Atrace
A
Atrace
2
1 1
22
=+=





∂
∂
=
∂
∂
=





∂
∂
∑∑= =
1
1
( ) ( ) 1−
=
∂
∂ kT
k
Ak
A
Atrace
Proof:
( ) ( ) ( ) ( ) ( ) 1111 −−−−
=+++=
∂








⋅∂
=
∂
∂ kT
k
kTkTkT
k
k
AkAAA
A
AAAtrace
A
Atrace
  



q.e.d.

273. 274
SOLO Matrices
Trace of a Square Matrix
The trace of a square matrix is defined as ( ) ( )T
nn
n
i
iinn AtraceaAtrace ×
=
× == ∑1
:
Proof:
q.e.d.
1
2
( ) T
A
A
e
A
etrace
=
∂
∂
( ) ( ) ( ) T
A
n
k
n
k
kT
n
kk
kT
n
n
k
k
n
n
k
k
n
A
eA
k
A
k
k
k
A
trace
Ak
A
trace
AA
etrace
===





∂
∂
=





∂
∂
=
∂
∂
∑ ∑∑∑ = =
→∞
→−
−
→∞
=
→∞
=
→∞
1 0
1
1
00 !
1
lim
!
lim
!
lim
!
lim
1
3
( )( ) ( )( ) ( )
( ) ( )( ) ( )( ) ( )
( ) ( )( ) ( )( ) ( )
TT
TTTTTTTTT
TTTTT
TTT
BACBAC
A
ACABtrace
A
BACAtrace
A
ABACtrace
A
CABAtrace
A
BACAtrace
A
CABAtrace
A
ACABtrace
A
BACAtrace
A
ABACtrace
+=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
111
21
11
( ) ( ) ( ) ( ) ( )
( ) TTTT
TTT
BACBACCABBAC
A
ABACtrace
A
ABACtrace
A
ABACtrace
+=+==
∂
∂
+
∂
∂
=
∂
∂ + 86
2
2
1
1
Proof: q.e.d.
1
4
( ) ( )( )
A
A
AAtrace
A
AAtrace TT
2
13
=
∂
∂
=
∂
∂
Table of Content

274. 275
Functional AnalysisSOLO
Inner Product
If X is a complex linear space, for the Inner Product < , > between
the elements (a complex number) is defined by:
Xzyx ∈∀ ,,
><>=< xyyx ,,1 Commutative law
><+>>=<+< zxyxzyx ,,,2 Distributive law
Cyxyx ∈∀><>=< λλλ ,,3
00,&0, =⇔=><≥>< xxxxx4
Define: ( ) ( ) ( ) ( ) ( )
( )
( )
( )
( )
( )









=










==>< ∫
tg
tg
tg
tf
tf
tfdttgtftgtf
nn
T

11
,:,
Table of Content

275. 276
SignalsSOLO
Signal Duration and Bandwidth
then
( ) ( )∫
+∞
∞−
−
= tdetsfS tfi π2
( ) ( )∫
+∞
∞−
= fdefSts tfi π2
t
t∆2
t
( ) 2
ts
f
f
f∆2
( ) 2
fS
( ) ( )
( )
2/1
2
22
:














−
=∆
∫
∫
∞+
∞−
+∞
∞−
tdts
tdtstt
t
( )
( )∫
∫
∞+
∞−
+∞
∞−
=
tdts
tdtst
t
2
2
:
Signal Duration Signal Median
( ) ( )
( )
2/1
2
22
2
4
:














−
=∆
∫
∫
∞+
∞−
+∞
∞−
fdfS
fdfSff
f
π ( )
( )∫
∫
∞+
∞−
+∞
∞−
=
fdfS
fdfSf
f
2
2
2
:
π
Signal Bandwidth Frequency Median
Fourier

276. 277
Signals
( ) ( )∫
+∞
∞−
= fdefSts tfi π2
SOLO
Signal Duration and Bandwidth (continue – 1)
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )∫∫ ∫
∫ ∫∫ ∫∫
∞+
∞−
∞+
∞−
∞+
∞−
−
∞+
∞−
∞+
∞−
−
∞+
∞−
∞+
∞−
∞+
∞−
=







=








=







=
dffSfSdfdesfS
dfdefSsdfdefSsdss
tfi
tfitfi
ττ
τττττττ
π
ππ
2
22
( ) ( )∫
+∞
∞−
= fdefSts tfi π2 ( ) ( ) ( )∫
+∞
∞−
== fdefSfi
td
tsd
ts tfi π
π 2
2'
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )∫∫ ∫
∫ ∫∫ ∫∫
∞+
∞−
∞+
∞−
∞+
∞−
−
+∞
∞−
+∞
∞−
−
+∞
∞−
+∞
∞−
−
+∞
∞−
=







−=








−=







−=
dffSfSfdfdesfSfi
dfdesfSfidfdefSfsidss
tfi
tfitfi
222
22
2'2
'2'2''
πττπ
ττπττπτττ
π
ππ
( ) ( )∫∫
+∞
∞−
+∞
∞−
= dffSds
22
ττ
Parseval Theorem
From
From
( ) ( )∫∫
+∞
∞−
+∞
∞−
= dffSfdtts
2222
4' π

277. 278
Signals
( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )∫
∫
∫
∫ ∫
∫
∫ ∫
∫
∫
∫
∫
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
+∞
∞−
−
∞+
∞−
+∞
∞−
+∞
∞−
−
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
=====
dffS
fd
fd
fSd
fS
i
dffS
fdtdetstfS
dffS
tdfdefStst
dffS
tdtstst
tdts
tdtst
t
fifi
22
2
2
2
22
2
2
:
π
ππ
SOLO
Signal Duration and Bandwidth
( ) ( )∫
+∞
∞−
−
= tdetsfS tfi π2
( ) ( )∫
+∞
∞−
= fdefSts tfi π2
Fourier
( ) ( )∫
+∞
∞−
−
−= tdetsti
fd
fSd tfi π
π 2
2
( ) ( )∫
+∞
∞−
= fdefSfi
td
tsd tfi π
π 2
2
( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )∫
∫
∫
∫ ∫
∫
∫ ∫
∫
∫
∫
∫
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
+∞
∞−
∞+
∞−
+∞
∞−
+∞
∞−
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
−
=








====
tdts
td
td
tsd
tsi
tdts
tdfdefSfts
tdts
fdtdetsfSf
tdts
fdfSfSf
fdfS
fdfSf
f
fifi
22
2
2
2
22
2
2222
:
ππ
ππππ

278. 279
Signals
( ) ( ) ( ) ( ) ( )∫∫∫∫∫
+∞
∞−
+∞
∞−
+∞
∞−
+∞
∞−
+∞
∞−
=≤








dffSfdttstdttsdttstdtts
222222
2
2
4'
4
1
π
( ) ( )∫∫
+∞
∞−
+∞
∞−
= dffSdts
22
τ
SOLO
Signal Duration and Bandwidth (continue – 1)
0&0 == ftChange time and frequency scale to get
From Schwarz Inequality: ( ) ( ) ( ) ( )∫∫∫
+∞
∞−
+∞
∞−
+∞
∞−
≤ dttgdttfdttgtf
22
Choose ( ) ( ) ( ) ( ) ( )ts
td
tsd
tgtsttf ':& ===
( ) ( ) ( ) ( )∫∫∫
+∞
∞−
+∞
∞−
+∞
∞−
≤ dttsdttstdttstst
22
''we obtain
( ) ( )∫
+∞
∞−
dttstst 'Integrate by parts
( )



=
+=
→



=
=
sv
dtstsdu
dtsdv
stu '
'
( ) ( ) ( ) ( ) ( )∫∫∫
+∞
∞−
+∞
∞−
∞+
∞−
+∞
∞−
−−= dttststdttsstdttstst '' 2
0
2

( ) ( ) ( )∫∫
+∞
∞−
+∞
∞−
−= dttsdttstst 2
2
1
'
( ) ( )∫∫
+∞
∞−
+∞
∞−
= dffSfdtts
2222
4' π
( )
( )
( )
( )
( )
( )
( )
( )∫
∫
∫
∫
∫
∫
∫
∫
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
∞+
∞−
+∞
∞−
=≤
dffS
dffSf
dtts
dttst
dtts
dffSf
dtts
dttst
2
222
2
2
2
222
2
2
44
4
1
ππ
assume ( ) 0lim =
→∞
tst
t

279. 280
SignalsSOLO
Signal Duration and Bandwidth (continue – 2)
( )
( )
( )
( )
( )
( )
    
22
2
222
2
2
4
4
1
ft
dffS
dffSf
dtts
dttst
∆
∞+
∞−
+∞
∞−
∆
∞+
∞−
+∞
∞−




























≤
∫
∫
∫
∫ π
Finally we obtain
( ) ( )ft ∆∆≤
2
1
0&0 == ftChange time and frequency scale to get
Since Schwarz Inequality: becomes an equality
if and only if g (t) = k f (t), then for:
( ) ( ) ( ) ( )∫∫∫
+∞
∞−
+∞
∞−
+∞
∞−
≤ dttgdttfdttgtf
22
( ) ( ) ( ) ( )tftsteAt
td
sd
tgeAts tt
ααα αα
222:
22
−=−=−==⇒= −−
we have ( ) ( )ft ∆∆=
2
1
Table of Content