The document presents a mathematical model of gear backlash, detailing the interaction of two masses under translational motion within a moving vehicle. It explains the different scenarios of gear contact and the corresponding equations of motion, emphasizing the implications of production tolerances leading to backlash. Additionally, it discusses the impact of gear engagement and disengagement on motion dynamics, providing examples and equations related to the transfer of forces and moments during these interactions.

1. 1
Backlash Simulation
SOLO HERMELIN
Updated: 26.11.06
25.02.11
No Backlash Backlash
http://www.solohermelin.com

2. 2
SOLO Backlash
Introduction
Two masses interacting with translational motion inside a moving vehicle
Backlash Mathematical Model
Spur Gear
Motor Moment Equation
Load Moment Equation
Contact Moment
Backlash Error
Backlash Logic
MATLAB Program
Simulation Results
References
Teeth Collision

3. 3
SOLO Backlash
Gears are used to transmit torque between rotating
axes using teeth. In a perfect Gear System, the
tooth of one axis Gear is always in Contact with the
tooth of the Gear of the other axis.
Because of production tolerances, during the
rotation the teeth Contact is lost for a small angle,
until is reestablished. This is the Gear Backlash.

4. 4
SOLO Backlash
To develop the Backlash model we must deal with the following
cases:
Because of production tolerances, during the rotation the teeth
Contact is lost for a small angle, until is reestablished. This is the
Gear Backlash.
(1) No Contact between the teeth of the two axes.
In this case the rotation dynamics of each axis is independent.
(2) Contact between the teeth of the two axes is just established.
In this case an equal impulse is transferred between the
teeth in Contact that will produce a change in angular velocity
of the two axes.
(3) A Continuous Contact between mating teeth exists.
In this case the rotation rate of the two axes is coupled and
defined by the Gear Teeth Ratio. The Moments transferred
between the two axes are such that the rotation rates and
rotation accelerations are coupled.
(4) Contact Lost (Disengagement), when the mating teeth lose Contact.
To get a understanding of the Backlash that involves rotation of
two axes let start with a simpler example of one dimensional
translation of two body that interact inside a moving vehicle, as
seen in the Figure. Return to the Table of Content

5. 5
SOLO Backlash
Consider a simple example (one dimensional translation) of a vehicle moving with
a known velocity VB (t). Inside the vehicle we have two masses:
1. m1 of coordinate x1 on which an external force F1 is applied
2. m2 of coordinate x2 on which an external force F2 is applied
When the masses are in contact a internal force F12, between the two masses, applies.
We can see that we have the physical constraint: - δBL ≤ x2-x1 ≤δBL
Two Masses Interacting with Translational Motion inside a Moving Vehicle

6. 6
SOLO Backlash
Equations of Motion
1. No contact between m1 and m2
( )
( )
BLBL
BD
BD
xx
VFF
m
x
VFF
m
x
δδ <−<−







−−=
−−=
12
2
2
2
1
1
1
2
1
1
1


2. Contact between m1 and m2
( )
( )
BL
BD
BD
xx
VFFF
m
x
VFFF
m
x
δ±=







−−−=
−−+=
12
122
2
2
121
1
1
2
1
1
1


21, FF - known applied forces on m1 and
m2, respectively
21, DD FF - known disturbance forces on m1 and
m2, respectively
( ) ( )
21
1221
12
12
mm
FFmFFm
xx
DD −−−
=− 
( ) ( )
BL
DD
xxF
mm
mm
mm
FFmFFm
xx δ±=
+
−
−−−
=− 1212
21
21
21
1211
12
12

Two Masses Interacting with Translational Motion inside a Moving Vehicle

7. 7
SOLO Backlash
Equations of Motion (continue – 1)
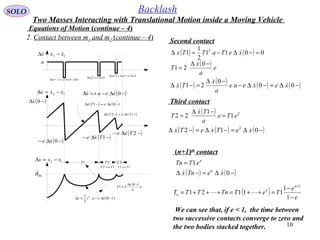
At collision between m1 and m2 a transfer of linear impulse ΔP occurs between the two masses
( )( ) ( )( )[ ] ( )( ) ( )( )[ ]
( ) ( )[ ] ( ) ( )[ ]−−+−=−−+=
−+−++−=−+−++=∆=∆
222111
22211112
xxmxxm
xVxVmxVxVmtFP BBBB


or
( ) ( )[ ] ( ) ( )[ ] 0222111 =−−++−−+ xxmxxm 
The second equation is obtained by using the elastic coefficient
of collision e (e = 0, for plastic collision and e =1 for an elastic
collision), that is defined as:
We obtain one equation with two unknowns ( ) ( )++ 21 , xx 
( ) ( )
( ) ( )
( )[ ] ( )[ ]
( )[ ] ( )[ ]−+−−+
++−++
−=
−−−
+−+
−=
21
21
21
21
:
xVxV
xVxV
VV
VV
e
BB
BB

 ( ) ( )
( ) ( )−−−
+−+
−=
21
21
xx
xx
e


or
We have x2 = x1 - δBL if before contact (-) ( ) ( ) 012 <−−− xx 
We have x2 = x1 +δBL if before contact (-) ( ) ( ) 012 >−−− xx 
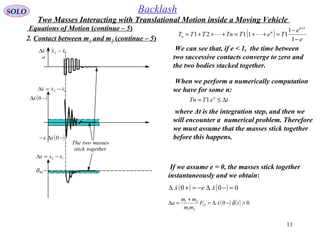
2. Contact between m1 and m2 (continue – 1)
Two Masses Interacting with Translational Motion inside a Moving Vehicle

8. 8
SOLO Backlash
Equations of Motion (continue – 2)
Now we have two equations with two unknowns:
or
Solving for , we obtain:( ) ( )++ 21 ,xx 
( ) ( ) ( ) ( ) ( ) ( )−++−−=++ 22121121 1 xmexemmxmm 
( ) ( ) ( ) ( ) ( ) ( )−−+−+=++ 21211221 1 xemmxmexmm 
( ) ( ) ( )
( )
( ) ( )[ ]−−−
+
+
+−=+ 12
21
2
11
1
xx
mm
me
xx 
( ) ( ) ( )
( )
( ) ( )[ ]−−−
+
+
−−=+ 12
21
1
22
1
xx
mm
me
xx 
2. Contact between m1 and m2 (continue – 2)
( )
( )
( ) ( )[ ]−−−
+
+
=∆=∆ 12
21
21
12
1
xx
mm
mme
tFP ( ) ( )[ ] ( ) ( )[ ]−−+−=−−+=∆=∆ 22211112 xxmxxmtFP  or
1F
2m
1x
2x
BV
1m
BLδ
1 2
P∆P∆
BLδ
0&12 >∆=− Pxx BLδ
2F
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )−−−=+−+
−+−=+++
1221
22112211
xexexx
xmxmxmxm


Two Masses Interacting with Translational Motion inside a Moving Vehicle

9. 9
SOLO Backlash
Equations of Motion (continue – 3)
( ) ( )
BL
aa
DD
xxa
F
mm
mm
mm
FFmFFm
xx
δ±≠=∆
+
−
−−−
=−
∆
12
12
21
21
21
1221
12
0
12
  

2. Contact between m1 and m2 (continue – 3) Let solve at contact x2 = x1 +δBL
( ) 00 >−∆ x
Let assume, for simplicity, that
during contact phase: 0>= consta
We have:
( ) ( ) 000 <−∆−=+∆ xex 
( ) ( ) ( )−∆−=+∆+=∆ 00 xeatxattx 
( ) ( )−∆−=∆ 0
2
1 2
xetattx 
Next contact
( ) ( ) 0011
2
1
1 2
=−∆−=∆ xeTaTTx 
( ) e
a
x
T
∆
−∆
=
0
21

( ) ( ) ( ) ( )−∆=−∆−
−∆
=−∆ 00
0
21 xexeae
a
x
Tx 


( ) ( ) ( ) 00112
21
21
>−∆+=
+
=∆ txeF
mm
mm
a δ
Two Masses Interacting with Translational Motion inside a Moving Vehicle

10. 10
SOLO Backlash
Equations of Motion (continue – 4)
2. Contact between m1 and m2 (continue – 4)
Second contact
( ) ( ) 0011
2
1
1 2
=−∆−=∆ xeTaTTx 
( ) e
a
x
T
−∆
=
0
21

( ) ( ) ( ) ( )−∆=−∆−
−∆
=−∆ 00
0
21 xexeae
a
x
Tx 


Third contact
( ) 2
1
1
22 eTe
a
Tx
T =
−∆
=

( ) ( ) ( )−∆=−∆=−∆ 012 2
xeTxeTx 
(n+1)th
contact
n
eTTn 1=
( ) ( )−∆=−∆ 0xeTnx n

We can see that, if e < 1, the time between
two successive contacts converge to zero and
the two bodies stacked together.
( ) e
e
TeTTnTTT
n
n
n
−
−
=++=+++=
+
1
1
11121
1

Two Masses Interacting with Translational Motion inside a Moving Vehicle
12 xxx  −=∆
a
12 xxx −=∆
BLδ
1T 2T 3T
12 TeT = 13 TeT =
( ) txeatx −∆−=∆ 0
2
1 2

( ) e
a
x
T
−∆
=
0
21

12 xxx  −=∆
( )−∆ 0x
( )−∆− 0xe 
( ) ( )−∆=−∆ 01 xeTx 
( )−∆− 1Txe 
( ) ( )−∆=−∆ 12 TxeTx 
( )−∆− 2Txe 
( )−∆−=∆ 0xeatx 
( ) ( ) ( )txea δ−∆+−=∆ 011 
12 aea ∆=∆
223 2
aeaea ∆=∆=∆

11. 11
SOLO Backlash
Equations of Motion (continue – 5)
12 xxx  −=∆
a
12 xxx −=∆
BLδ
12 xxx  −=∆
( )−∆ 0x
( )−∆− 0xe 
The two masses
stick together
2. Contact between m1 and m2 (continue – 5)
We can see that, if e < 1, the time between
two successive contacts converge to zero and
the two bodies stacked together.
If we assume e = 0, the masses stick together
instantaneously and we obtain:
( ) ( ) 000 =−∆−=+∆ xex 
When we perform a numerically computation
we have for some n:
teTTn n
∆≤= 1
where Δt is the integration step, and then we
will encounter a numerical problem. Therefore
we must assume that the masses stick together
before this happens.
( ) ( ) 0012
21
21
>−∆=
+
=∆ txF
mm
mm
a δ
Two Masses Interacting with Translational Motion inside a Moving Vehicle
( ) e
e
TeTTnTTT
n
n
n
−
−
=++=+++=
+
1
1
11121
1


12. 12Serway and Jewett,“Physics for Scientists and Engineers”, 6th
Ed.,

13. 13
SOLO Backlash
Equations of Motion (continue – 6)
Let see what are the equation of motion when the two masses stick together ( x1(t) = x2 (t) for a
nonzero period of time).
In this case
( )
( )






−−−=
−−+=
BD
BD
VFFF
m
x
VFFF
m
x


2
1
122
2
1
121
1
1
1
1
( )
( ) ( )
( )21
12221
12
21
221
21
1
1
mm
FFmFFm
F
V
mm
FFFF
xx
DD
B
DD
+
−−−
=
−
+
−−+
== 
From the Figures bellow the masses will stick together as long as ( ){ } 01212 >−⋅ xxFsign
Two Masses Interacting with Translational Motion inside a Moving Vehicle

14. 14
SOLO Backlash
Equations of Motion (continue – 7)
1F
1DF
12F
12F
2DF
12F
2F
( ) ( ) ( )
( )
( ) ( )[ ]−−−
+
+
−−=+ 12
21
1
22
1
xx
mm
me
xx 
2
1
m s
1
s
1
BV
2x
BL
( ) ( ) ( )
( )
( ) ( )[ ]−−−
+
+
+−=+ 12
21
2
11
1
xx
mm
me
xx 
1
1
m s
1
s
1
BV
1x
BL
( )
( ) ( )
( )11
21
2
2
21
1
2 DD FF
mm
m
FF
mm
m
−
+
−−
+
2x
12 xx −
BL
1
0 12 xx −
BLδBLδ−
1x
2x
12F
( )121 2 xxF −
1 ( )[ ]1212 xxFsign −
AND
BL
Stick
mode
Two Masses Interacting with Translational Motion inside a Moving Vehicle
Return to the Table of Content

15. 15
SOLO Backlash
Backlash Mathematical Model
Motor Moment Equation
m
DmrmCT
Bm
J
TTiK −−
+= ωθ 
  
( )

InertiaMotor
Bmm
eDisturbanc
Dm
Torque
ction
rm
Command
Torque
put
CT JTTiK ωθ −=−−
ReIm
- command currentCi
- moment of inertia of the rotor along it’s rotational axismJ
- rotor gear angle and it’s first and second order derivativemmm θθθ  ,,
- angular rate and acceleration of the bodyBB ωω ,
- reaction torque of the gimbals gear on the rotor gearrmT
-disturbance torque on the rotor (friction, mass-unbalance,
inertia cross-coupling) – not a function of
DmT
mθ
Return to the Table of Content

16. 16
Spur Gear Nomenclature
Pitch circles – Theoretical circles upon which all
calculations are based with centers
O1 and O2 and diameters D1 and D2.
The two pitch circles are tangent at
the pitch point P.
Pressure Lines – The lines passing through P and
making
an angle φ with the tangent to the pitch
circles along which the tooth of one gear
presses the tooth of the second gear.
Base circles – Circles tangent to pressure line
with centers O1 and O2 and diameters
DB1 and DB2.
ϕϕ cos&cos 2211 DDDD BB ==
Circular pitch p – The distance measured along the pitch
circle from a point on one tooth to the
corresponding point on the adjacent
point. Since we assume that the two
gears always maintain contact during
rotation the circular pitches are equal.
N1, N2 – Number of teeth on the two gears.
ω1, ω2 – Angular rates of the two gears.
2211 ωω NN =
2
2
1
1
N
D
N
D
p
ππ
==
1
2
2
1
2
1
ω
ω
==
N
N
D
D
SOLO
Pitch
Circles
P
O1
O2
R1
R2
Base
Circles
ϕ
RB1
RB2
ϕ
PressureLine 1
Pressure
Line 2

17. 17
A
Begin
contact
End
contact
B
CContact Line 1
(Involute)
A'
B'
Contact Line 2
(Involute)
rF
Pressure
Line 1
PressureLine 2
Reaction
Force
rF
Reaction
Force
Spur Gear Teeth
Spur Gear Tooth shape must be such that
contact between the tooth of one gear to the
corresponding tooth of the second gear is
continuously maintained until the contact
occurs with the adjacent tooth.
If the shapes of the teeth on the two gears
have this property they are called conjugates.
From the figure we can see that during the
rotation of the driver the contact begins at
point A and continues until it ends at point B.
The segment AB is on the pressure line.
Among infinite possibilities of conjugate
shapes the one that is almost exclusively used
in the gear design is the involute.
SOLO

18. 18
Spur Gear Teeth
Among infinite possibilities of conjugate
shapes the one that is almost exclusively used
in the gear design is the involute.
The involute of a circle (base circle) is obtained
by an imaginary string IA (see Figures) wound on
the circle and then unwounded (IC, IB(,
while holding it taut.
Base circle
O
β
I
θ ψ
A
β
1BR
β1B
R
r
x
y
Cβ
Cθ Cr
( )θ,rB
( )CCrC θ,
( )
( )βββ
βββ
cossin
sincos
1
1
−=
+=
B
B
Ry
Rx
The involute equation
The involute has the following properties:
1.All lines normal to the involute are tangent
to the base circle
2.The radius of curvature of the involute at
a point P (r,θ) is given by ρ=RB1β. The base
circle is the locus of the center of curvature
of the involute.
SOLO

19. 19
Spur Gear Teeth
In the same way
Point A on the involute has the radius RA and the
thickness tA along the circle RA.
SOLO
A
B
AR
BR
bR
Aφ
Bφ
2/Bt
2/At
O
E
D
FG
tooth
involute
base
circle
B
involute
OG
BG
OG
DG
DOG φtan===∠
∩
BBBB invDOGDOB φφφφ =−=−∠=∠ :tan
AAA invDOA φφφ =−=∠ :tan
Point B on the involute has the radius RB and the
thickness tB along the circle RB.
A
A
A
A
A
R
t
inv
R
t
DOADOE 2
1
2
1
+=+∠=∠ φ
B
B
B
B
B
R
t
inv
R
t
DOBDOE 2
1
2
1
+=+∠=∠ φ






−+= BA
B
A
BB invinv
R
t
Rt φφ
2
2

20. 20
Width of
space
Face width
Top land
Addendum
circle
Tooth
thicknessAddendum
Dedendum
Dedendum
circle
Clearence
circle
Clearence
Pitch
circle
Face
Flank
Bottom
land
Spur Gear TeethSOLO
Addendum – the radial distance between the top land of the tooth and the pitch circle
Dedendum – the radial distance between the bottom land of the tooth and the pitch circle
Addendum circle – the circle passing through the top land of the tooth
Dedendum circle – the circle passing through the bottom land of the tooth
Clearance circle – the circle tangent to the addendum of the mating gear

21. 21
Spur Gear Force EquationSOLO
If no backlash rmθm = rLθL
L
m
L
m
r
r
θθ 





=
load
L
motor
m
N
D
N
D
p
ππ
==
Mating condition of the teeth on the two gears is
Circular path of gear 1 = Circular path of gear 2
L
motor
load
m
L
m
L
N
N
N
D
D
r
r
=== : LLL
motor
load
L
m
L
m N
N
N
r
r
θθθθ  =







=







=
The force applied by gear 1 on gear 2 is Fr . Since the tooth surface shape is an involute
and the force at the point of contact is normal to the surface, it will be tangent to the base
circle that defines the involute. Therefore Fr will always be on the pressure line and
tangent to both base circles.
 
ϕϕ cos
3'
cos L
th
m r
bL
rL
LawsNewton
r
r
bm
rm
r
T
F
r
T
==
L
rL
rL
L
m
rL
L
m
rm
N
T
T
N
N
T
r
r
T ===
Pressure line 1
Base circle
Pitch circle
Pitch circle
Base circle
P B
Pinion
(driver)
Gear
(driven)
C
O1
ϕ
Begin
contact
End
contact
A
rF
rF
bmr mr
bLr
Lr
ϕ
ϕ
Trm, TrL are the reaction
moments on the two gears
Return to the Table of Content

22. 22
SOLO Backlash
Load Moment Equation
( ) LDLBm
L
LLDLBLLrmLLm TT
N
JTTJTNT ++





+=+++== ωθωθ  1
- moment of inertia of the load (including all the parts
attached to it) along it’s rotational axis
LJ
- load gear angle and it’s first and second order derivativeLLL θθθ  ,,
- torque applied by the motor gear on the load gearrLT
where
-disturbance torque on the load (friction, mass-unbalance,
inertia cross-coupling) – not a function of
DLT
Lθ
- torque applied on the load gearLT
L
LDLrmL
BL
J
TTTN −−
+−= ωθ 
or
Return to the Table of Content

23. 23
SOLO Backlash
From this equation we can find the moment Trm necessary to stick the
motor gear to the gimbals gear is:
L
LDL
BB
m
DmrmCT
LL
L
L
rL
rm
N
TT
J
TTiK
NN
J
N
T
T
+
+





+





+
−−
== ωω 
1
( )[ ] ( )
2
2
1
1
1
1
LmL
LDLmLBLmDmCTL
Lm
L
L
LDL
BB
m
DmCT
LL
L
rm
NJJ
TTJNNJTiKJ
NJ
J
N
TT
J
TiK
NN
J
T STICK
+
++++−
=
+
+
+





+





+
−
=
ω
ωω


m
DmrmCT
Bm
J
TTiK −−
=−ωθ 
L
LDLrmL
BL
J
TTTN −−
=+ωθ 
Contact Moment
Return to the Table of Content

24. 24
SOLO Backlash
Define the backlash error
LLmBL N θθε −=:
Then
BLBLIF θε < 0=rmT 0== rmLrL TNT
BLBLIF θε ≥ STICKrmrm TT = rmLrL TNT =
Backlash Error
Return to the Table of Content

25. 25
SOLO Backlash
Let find what happens at the collision
of the teeth of the gears.
( )
→
−== trV BmmOmM
I
M 1ωθρ 
The velocity at the point M on the motor gear is:
The velocity at the point L on the load gear is:
( ) ( )
( )
→
→→
−=
+++−=+=
trr
trtrrV
BmLL
BLLBLmLO
I
OO
I
L LLm
1
11
ωθ
ωθωρρ


Teeth Collision
(1) No Contact between the teeth of the two axes.
In this case the rotation dynamics of each axis is independent.

26. 26
SOLO Backlash
The collision between toot M and L will produce an equal and opposite
impulse Pr on the gear tooth, that will produce reaction impulses on the gear
axes, and a change in angular impulse on both gears (ΔHm, ΔHL)
( )[ ] ( )[ ]
( ) ( )[ ] mrmmm
BmmBmmm
rPJ
JJH
∆−=−−+=
−−−−+=∆
θθ
ωθωθ


( )[ ] ( )[ ]
( ) ( )[ ] LrLLL
BLLBLLL
rPJ
JJH
∆=−−+=
+−−++=∆
θθ
ωθωθ


( ) ( )−− Lm θθ  , and are the angular
rates of the motor and gimbals gears, respectively,
before (-) and after(+) the collision.
( ) ( )++ Lm θθ  ,
We obtain the following equations
( ) ( )[ ] ( ) ( )[ ]−−+−=−−+=∆ mmm
m
LLL
L
r J
r
J
r
P θθθθ  11
Teeth collision (continue – 1)

27. 27
SOLO Backlash
The second equation is obtained by using the
elastic coefficient of collision e (e = 0, for plastic
collision and e =1 for an elastic collision), that is
defined as:
( ) ( )[ ] ( ) ( )[ ]−−+−=−−+=∆ mmm
m
LLL
L
r J
r
J
r
P θθθθ  11
or
( ) ( )[ ] ( ) ( )[ ] 0=−−++−−+ mmmLLLL JNJ θθθθ 
We obtain one equation with two unknowns ( ) ( )++ Lm θθ  ,
( ) ( )
( ) ( )
( )[ ] ( )[ ]
( )[ ] ( )[ ]
( ) ( )
( ) ( )
( ) ( )
( ) ( )−−−
+−+
−=
−−−
+−+
−=
−−−−−
−+−−+
−=
−−−
+−+
−=
mLL
mLL
mmLL
mmLL
BmmmBmLL
BmmmBmLL
ML
ML
N
N
rr
rr
rrrr
rrrr
VV
VV
e
θθ
θθ
θθ
θθ
ωθωθ
ωθωθ






:
Teeth collision (continue – 2)

28. 28
SOLO Backlash
or:
Now we have two equations with two unknowns ( ) ( )++ Lm θθ  ,
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )



−−−=+++−
−+−=+++
LLmLLm
LLmmLLLmmL
eNeN
JJNJJN
θθθθ
θθθθ


Solving for we obtain( ) ( )++ Lm θθ  ,
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )−−+−+=++
−++−−=++
LmLLmmLGmLL
LLLmLmLmmLL
JNeJJNeJNJ
JNeJeJNJNJ
θθθ
θθθ


22
22
1
1
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
−−=+ LLm
mLL
L
mm N
JNJ
Je
θθθθ 
2
1
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
+−=+ LLm
mLL
mL
LL N
JNJ
JNe
θθθθ 
2
1
Teeth collision (continue – 3)
Also
( ) ( )[ ] ( ) ( ) ( )[ ]−−−
+
+
=−−+−=∆=∆ LLm
mLL
Lm
mmmmrrm N
JNJ
JJe
JrPtT C
θθθθ 
2
1

29. 29
SOLO Backlash
Let compute ( ) ( )+−+ LLm N θθ 
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
−−=+ LLm
mLL
L
mm N
JNJ
Je
θθθθ 
2
1
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
+−=+ LLm
mLL
mL
LL N
JNJ
JNe
θθθθ 
2
1
Teeth collision (continue – 4)
( ) ( ) ( )
( )
( )
( ) ( ) ( )[ ]−−−





+
+
−
+
+
−=+−+ LLm
mLL
mL
mLL
L
LLm N
JNJ
JNe
JNJ
Je
N θθθθ 
2
2
2
11
1
or
( ) ( ) ( ) ( )[ ]−−−−=+−+ LLmLLm NeN θθθθ 
We can see that
( ) ( )[ ] ( ) ( )[ ]−−−−=+−+ LLmLLm NsignNsign θθθθ 

30. 30
SOLO Backlash
LLmBL N θθε  −=
θa
BLθ
1T 2T 3T
12 TeT = 13 TeT =
( ) teat BLBL −−∆= 0
2
1 2
εε 
( ) e
a
T BL
∆
−
=
0
21
ε
( )−0BLε
( ) ( )−+−=∆ 011 BLea εθ

12 θθ aea ∆=∆
23 θθ aea ∆=∆
LLmBL N θθε  −=
( )−− 0BLe ε
( )−− 1Te BLε ( )−− 2Te BLε
( ) ( )−=− 12 TeT BLBL εε 
( ) ( )−=− 01 BLBL eT εε 
LLmBL N θθε −=
( )−−= 0BLBL eat εε θ

Let solve at collision
( ) 00 >−BLε
Let assume, for simplicity, that
during contact phase: 0>= constaθ
We have:
( ) ( ) 000 <−−=+ BLBL e εε 
( ) ( ) ( )−−=++= 00 BLBLBL eatatt εεε θθ

( ) ( )−−= 0
2
1 2
BLBL etatt εε θ

Next contact
( ) ( ) 0011
2
1
1 2
=−−= BLBL eTaTT εε θ

( ) e
a
T BL
θ
ε −
=
0
21

( ) ( ) ( ) ( )−=−−
−
=− 00
0
21 BLBL
BL
BL eeae
a
T εε
ε
ε θ
θ



Teeth collision (continue – 5)
L
LDLrmL
BL
J
TTTN −−
+−= ωθ 
m
DmrmCT
Bm
J
TTiK −−
+= ωθ 
( ) ( ) ( )teT
JJ
JNJ
T
JJ
JNJ
T
JJ
JNJ
N
BL
a
rm
mL
mLL
rm
mL
mLL
rm
mL
mLL
LLmBL
STICK
STICK
δε
θθε
θ
−+−
+
=
+
−
+
=−=
01
2
22

  


31. 31
SOLO Backlash
The kinetic energy loss due to the collision is given by
( ) ( ) ( ) ( )
2
2222
2
1
2
1
2
1
2
1






+++−





−+−=∆ LLmmLLmmk JJJJE θθθθ 
( ) ( )
( ) ( )
( ) ( ) ( )[ ]
( ) ( )
( ) ( ) ( )[ ]
2
2
2
2
22
1
2
1
1
2
1
2
1
2
1






−−−
+
+
+−−






−−−
+
+
−−−
−+−=
LLm
mLL
mL
LL
LLm
mLL
L
mm
LLmm
N
JNJ
JNe
J
N
JNJ
Je
J
JJ
θθθ
θθθ
θθ



( )
( ) ( ) ( )[ ] ( ) ( )[ ]
( )
( )
( ) ( )[ ] ( )mLLLLm
mLL
mL
LLmLLm
mLL
mL
JNJN
JNJ
JJe
NN
JNJ
JJe
22
22
2
2
2
1
1
+−−−
+
+
−
−−−−−−
+
+
−=
θθ
θθθθ


( )
( ) ( ) ( )[ ]2
2
2
2
1
−−−
+
−
= LLm
mLL
mL
N
JNJ
JJe
θθ 
Teeth collision (continue – 6)

32. 32
SOLO Backlash
The kinetic energy loss due to the collision is given by
( )
( ) ( ) ( )[ ]2
2
2
2
1
−−−
+
−
=∆ LLm
mLL
mL
k N
JNJ
JJe
E θθ 
We can see that
1. If (soft touch) then( ) ( )−=− mLLN θθ 
( ) ( )−=+ mm θθ 
( ) ( )−=+ LL θθ 
0=∆ kE
2. If e = 1 (elastic collision)
0=∆ kE
3. The maximum kinetic energy loss is obtained when e = 0 (plastic collision)
( ) ( ) ( )[ ]2
2
2
−−−
+
=∆ LLm
mLL
mL
k N
JNJ
JJ
E MAX
θθ 
Teeth collision (continue – 7)
Return to the Table of Content

33. 33
SOLO Backlash
The backlash of two gears occurs because of thermal expansion and
tooth error at predefined angles. When backlash occurs the two gears
loose contact for a small angle.
For gear1 the lose of contact occurs every radians.
1
1
2
N
π
=Θ
For gear2 the lose of contact occurs every radians.
2
2
2
N
π
=Θ
1
1
2
N
π
=Θ
2
2
2
N
π
=Θ
12 Θ 13 Θ 14 Θ
24 Θ
23 Θ
22 Θ
1θ
2θ
2
2
1
2 θθ
N
N
=
1Θ−
2Θ−
BLθ2
Backlash Logic

34. 34
SOLO Backlash
Backlash Logic (continue - 1)
IF Backlash = .True. & Gears dynamically independentBLk θθ ≤Θ− 11
IF Backlash = .False. & Gears stick togetherBLk θθ >Θ− 11
No Backlash Backlash

35. 35
SOLO Backlash
Backlash Logic (continue - 2)
A
C C’
Contact Line
1
(Involute)
Contact Line
2
(Involute)A’
0>rF 0<rF
Each tooth has two contact lines:
Contact line 1 between points A and C
Contact line 2 between points A’ and C’
Contact line 1 of gear 1 (G1) touches
contact line 1 of gear 2 (G2) along the
pressure line 1. To keep the contact we
must have Fr > 0 (the reaction force
between G1 and G2).
Contact line 2 of gear 1 (G1) touches
contact line 2 of gear 2 (G2) along the
pressure line 2. To keep the contact we
must have Fr < 0 (the reaction force
between G1 and G2).
On pressure line 1 if
210 GG →>θ
120 GG →<θ
On pressure line 2 if
120 GG →>θ
210 GG →<θ
Gear Gi pushes gear GjGjGi →

36. 36
SOLO Backlash
Dynamic computations in contact
Compute
Contact Flag = .True.
[ ]
mr
LmL
DLmLBmDmCTL
rm rF
NJJ
TJNJTiKJ
T STICK
=
+
++−
= 2
ω
m
DmrmCT
Bm
J
TTiK −−
=−ωθ 
L
LDLrmL
BL
J
TTTN +−
=+ωθ 
Integrate both equations to obtain
BLBm ωθωθ +−  ,
Compute and integrate to obtainLm θθ  , Lm θθ ,
Backlash Logic (continue - 3)

37. 37
SOLO Backlash
Dynamic computations in contact (second way)
Compute
Contact Flag = .True.
[ ]
mr
LmL
DLmLBmDmCTL
rm rF
NJJ
TJNJTiKJ
T STICK
=
+
++−
= 2
ω
B
m
DmrmCT
m
J
TTiK
ωθ  +
−−
=
B
L
LDLrmL
L
J
TTTN
ωθ  −
+−
=
Integrate both equations to obtain
Lm θθ  ,
and integrate to obtain Lm θθ ,
Backlash Logic (continue - 4)

38. 38
SOLO Backlash
Detection of End of Contact
Contact ends if one of the following condition
occurs
Backlash Logic (continue - 5)
1. ( ) BL
m
mm
N
θ
π
θθθ −≥+−=∆
2
we must also have 0≥mθ
2. ( ) BL
m
mm
N
θ
π
θθθ +−≤+−=∆
2
we must also have 0≤mθ
When one of those events occurs Contact Flag changes from .True. to .False.
4. changes signSTICKrmT
0=BLεInitialize
3. ( )+−=∆ mm
θθθ
changes sign
it is enough to compute ( )+−=∆ mm θθθSince during contact we have LLm N θθ  =
and to check if change sign.mrmSTICK
T θ, Here is the motor gear position when Start Contact.( )+m
θ

39. 39
SOLO Backlash
Dynamic Computations if No Contact
Compute
Contact Flag = .False.
0== mrrm rFT
m
DmrmCT
Bm
J
TTiK −−
=−ωθ 
L
LDLrmL
BL
J
TTTN +−
=+ωθ 
Integrate both equations to obtain
BLBm ωθωθ +−  ,
Compute and integrate to obtainLm θθ  , Lm θθ ,
Backlash Logic (continue - 6)
Compute LLmBL N θθε  −=:
Integrate to obtainBLε BLε
If Start Contact Flag changes from .False. to .True. for one
computation cycle and in the next one back to .False.
BLBL θε ≥

40. 40
SOLO Backlash
Backlash Logic (continue - 7)
Contact Between Gears Teeth is Detected
( )[ ] ( )
mr
LmL
LDLmLBLmDmCTL
rm rF
NJJ
TTJNNJTiKJ
T STICK
=
+
++++−
= 2
1 ω
Compute
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
+−=+ mLL
mLL
L
mm N
JNJ
Je
θθθθ 
2
1
( ) ( ) ( )
( ) ( ) ( )[ ]−−−
+
+
−−=+ mLL
mLL
mL
LL N
JNJ
JNe
θθθθ 
2
1
on pressure line 1 if
210 GG →>θ
120 GG →<θIf 0>= mrrm rFT STICK
Contact begins at point A
Contact begins at point B
on pressure line 2 if
120 GG →>θ
210 GG →<θ
If 0<= mrrm rFT STICK
Contact begins at point C
Contact begins at point D
Contact Start changes from .False. to .True.
Store ( ) mθθ =+
Reinitialize the integrators using

41. 41
SOLO Backlash
Backlash Logic (continue - 8)
When Contact Start = .True. the elastic collisions
between gears teeth will occur and the time
between two successive collisions will be
( )
e
a
T
T nBL
n
θ
ε
2
1 −
= −

LLmBL N θθε  −=
θa
BLθ
( )−0BLε
The two gears
stick together
LLmBL N θθε  −=
( )−− 0BLe ε
LLmBL N θθε −=
1−nT nT
( )
e
a
T
T NBL
n
θ
ε
2
1 −
= −

We can see that if e=0 (plastic collision),
we have T1 = 0 and the teeth remain in
contact. In this case
Contact Flag = .True.
when Contact Start = .True.
0=eIf
( ) ( ) ( )
( ) ( ) ( )[ ]
0
2
1
=
−−−
+
+
+−=+
e
mLL
mLL
L
mm N
JNJ
Je
θθθθ 
( ) ( ) ( )
( ) ( ) ( )[ ]
0
2
1
=
−−−
+
+
−−=+
e
mLL
mLL
mL
LL N
JNJ
JNe
θθθθ 
STICKrm
mLL
Lm
T
JNJ
JJ
a 2
+
=θ
Contact Between Gears Teeth is Detected (continue - 1)
Reinitialize the integrators using

42. 42
SOLO Backlash
To prevent numerical problems, when
Contact Flag = .True.
Backlash Logic (continue - 9)
When Contact Start = .True. the elastic collisions
between gears teeth will occur and the time
between two successive collisions will be
( )
e
a
T
T nBL
n
θ
ε
2
1 −
= −

LLmBL N θθε  −=
θa
BLθ
( )−0BLε
The two gears
stick together
LLmBL N θθε  −=
( )−− 0BLe ε
LLmBL N θθε −=
1−nT nT
( )
e
a
T
T NBL
n
θ
ε
2
1 −
= −

tTn ∆≤
(where Δt is related to the integration
time), we say that the two gears teeth are
in continuous contact and we declare
To assure that the teeth gears are in
continuous contact, we will reinitialize
using e=0, for this
computation cycle.
( ) ( )++ 0,0 Lm θθ 
( ) ( ) ( )
( ) ( ) ( )[ ]
0
2
1
=
−−−
+
+
+−=+
e
mLL
mLL
L
mm N
JNJ
Je
θθθθ 
( ) ( ) ( )
( ) ( ) ( )[ ]
0
2
1
=
−−−
+
+
−−=+
e
mLL
mLL
mL
LL N
JNJ
JNe
θθθθ 
0≠eIf
STICKrm
mLL
Lm
T
JNJ
JJ
a 2
+
=θ
Return to the Table of Content
Contact Between Gears Teeth is Detected (continue - 2)

43. 43
SOLO Backlash
Equations of Motion (Summary)

44. 44
SOLO Backlash
Equations of Motion (Summary 1)
Return to the Table of Content

45. 45
SOLO Backlash
Backlash Logic (continue - 10)
When Contact Start = .True. instead of
performing reinitialization of integrals we can,
for one computation cycle, simulate the impulse
at collision.
LLmBL N θθε  −=
θa
BLθ
( )−0BLε
The two gears
stick together
LLmBL N θθε  −=
( )−− 0BLe ε
LLmBL N θθε −=
1−nT nT
( )
e
a
T
T NBL
n
θ
ε
2
1 −
= −

by using
Contact between gears is detected (continue - 1)
( ) ( ) ( )[ ]−−−
+
+
=∆=∆ LLm
mLL
Lm
mrrm N
JNJ
JJe
rPtT C
θθ 
2
1
( ) ( ) ( )[ ]−−−
+
+
∆
= LLm
mLL
Lm
rm N
JNJ
JJe
t
T C
θθ 
2
11

46. 46
SOLO Backlash
Equations of Motion (Summary 2)
Return to the Table of Content

47. 47
%Backlash
%
%Solo Hermelin, March 2006
%
%Simulates Backlash Effects of a Gear Transmission Driven by an Electric
%Motor to Move a Predefined Load
clear
%Default Parameters
dt=0.001;
DegtoRad = pi/180; %Transform fro Degrees to Radians
%Motor Parameters
Jmotor = 1.14e-6; %Motor Inertia [Kg*m^2[
%Jmotor = 1.; %Motor Inertia [Kg*m^2[
Nmotor = 36; % Number of theeth on motor gear
pmotor = 360/Nmotor; % Angle between two consecutive theeth on motor Gear (deg(
pmotorR = pmotor*DegtoRad; % Angle between two consecutive theeth on motor Gear (deg(
Backlash = .25; % Percent of Motor Gear Angle for which theeth lose contact
%Load Parameters
Jload = 8.5e-5; % Load Inertia [Kg*m^2[
%Jload = 1; % Load Inertia [Kg*m^2[
Nload = 72; % Number of theeth on load gear
NL = Nload/Nmotor; % Theeth Ratio
NLJm = NL*Jmotor;
NL2Jm = NL*NLJm;
JlNLJ2m=Jload+NL2Jm;
TfM = 0.; % Friction Moment on Motor
TfL = 0.; % Friction Moment on Load
Backlash
MATLAB Program (page 1)

48. 48
%Initialization of State-Variables
ThetM = 0.;
ThetM1Dot = 0.;
PhiM2Dot = 0.;
ThetL = 0.;
ThetL1Dot = 0.;
PhiL2Dot = 0.;
epsBL = ThetM - NL*ThetL;
StartContact = 0; % Has value 1 only for one integration cycle, when gear theeth make contact
Contact = 0.; % Change to 1 when gear theeth are in contact
k=0;
dt=input('Enter Integration Time Step (s(: '(;
tend=input('Enter Final Simultion Time (s(: '(;
Backlash=input('Enter Backlash (0-1(: '(;
el = input('Elasticity of Gear Theeth (0-1(: '(;
InMoment = input('Amplitude of Input Sinusoidal Moment (N*m(: '(;
freqin = input('Frequency of Sinusoidal Input (Hz(: '(;
Aomegab = input('Amplitude of Sinusoidal Body Rate (rad/sec(:'(;
fomegab = input('Frequency of Sinusoidal Body Rate (rad/sec(:'(;
omgi = 2*pi*freqin;
omgob =2*pi*fomegab;
labelBacklash=['Backlash =' num2str(Backlash( [;
labelel=['el =' num2str(el( [;
ThetBL = Backlash*pmotor; % Backlash angle at motor gear [deg[
ThetBLR = ThetBL*DegtoRad;
t=0;
Backlash
MATLAB Program (page 2)

49. 49
% Loop on time
while t<=tend
k = k+1;%plot index
% Inputs
KtIc = InMoment*cos(omgi*t(; %Sinusoidal Input [N*m[
%KtIc = InMoment;
Tload = 0.; % Load Moment [N*m[
OmegaB = Aomegab*sin(omgob*t(; % Body rate [rad/s[
OmegaDotB = Aomegab*omgob*cos(omgob*t(; % Body angular acceleration [rad/s^2[
epsDotBL = ThetM1Dot -NL*ThetL1Dot;
%Computation of Stiction Moment
TrmStick = ( Jload*(KtIc-TfM+Jmotor*(1+NL(*OmegaDotB(+NLJm*(Tload+TfL( (/JlNLJ2m;
Backlash
MATLAB Program (page 3)

50. 50
%Backlash Logic
if (Contact==0( & (abs(epsBL(>= ThetBLR(
StartContact = 1; % Integration cycle where theeth contact occurs
TMP =0.5* Jmotor*Jload*abs(epsDotBL(/(abs(TrmStick(*JlNLJ2m(;
if TMP<=dt
Contact = 1;
EndCntct1 = 0;
EndCntct2 = 0;
EndCntct3 = 0;
ThetM1Dot =ThetM1Dot -Jload*epsDotBL/JlNLJ2m; %Rate change due to Plastic Impact
ThetL1Dot =ThetL1Dot +NLJm*epsDotBL/JlNLJ2m; %Rate change due to Plastic Impact
Thetcntct = ThetM;
sgnTstck = sign (TrmStick(;
epsBL = 0.;
p = 0; % index
else
ThetM1Dot =ThetM1Dot -(1+el(*Jload*epsDotBL/JlNLJ2m; %Rate change due to Elastic Impact
ThetL1Dot =ThetL1Dot +(1+el(*NLJm*epsDotBL/JlNLJ2m; %Rate change due to Elastic Impact
Contact = 0;
end %TMP<=dt
end %(Contact==0( & (abs(epsBL(>= ThetBLR(
Backlash
MATLAB Program (page 4)

51. 51
if (Contact==1( & (StartContact==0(
%Check end of Contact
p = p + 1;
DelThetM = ThetM - Thetcntct;
if p==1
sgnDelThM = sign (DelThetM(;
end
if p>1
if (sign (DelThetM(~=sgnDelThM(
Contact = 0;
EndCntct1 = 1
elseif abs(DelThetM(>=(pmotorR-ThetBLR(
Contact = 0;
EndCntct2 = 1
end
end % p>1
if sign(TrmStick(~=sgnTstck
Contact = 0;
EndCntct3 = 1
end
end % (Contact==1( & (StartContact==0(
if (Contact==1(
Trm = TrmStick;
else % Contact=0
Trm = 0;
end % Contact==1
%End Backlash Logic
Backlash
MATLAB Program (page 5)

52. 52
%Motor Dynamics
ThetM2Dot = (KtIc-TfM-Trm(/Jmotor+OmegaDotB;
%Load Dynamics
ThetL2Dot = (NL*Trm-Tload-TfL(/Jload-OmegaDotB;
%Plot Data Preparation
T (k( = [t[;
ktic (k( = [KtIc[;
thetm (k( = [ThetM/DegtoRad[;
thethm1d (k( = [ThetM1Dot[;
thetm2d (k( = [ThetM2Dot[;
thetl (k( = [NL*ThetL/DegtoRad[;
thethl1d (k( = [NL*ThetL1Dot[;
thetl2d (k( = [NL*ThetL2Dot[;
epsBLD (k(= [epsBL/DegtoRad[;
epsD (k( = [(ThetM-NL*ThetL(/DegtoRad[;
epsdotBL (k( = [epsDotBL[;
strtcontct (k( = [StartContact[;
contct (k( = [Contact[;
Backlash
MATLAB Program (page 6)

53. 53
%Integration of State Variables
if StartContact == 1
StartContact =0;
else
ThetM1Dot = ThetM1Dot+ThetM2Dot*dt;
ThetL1Dot = ThetL1Dot+ThetL2Dot*dt;
end
if Contact==0
epsBL =epsBL + epsDotBL*dt;
end
ThetM = ThetM + ThetM1Dot*dt;
ThetL = ThetL + ThetL1Dot*dt;
t=t+dt;
end % of Time Loop t<=tend
figure(1(
plot(T,thetm2d ,'g-'(;
legend(labelBacklash,labelel(;
hold on;
plot(T,thetl2d ,'r-.'(;
hold off;
title('Angular Acceleration of Motor and Load Versus Time'(,
%axis([0 5 -1 1[(,
grid, xlabel('Time (s('(, ylabel('ThetM2dot, NL*ThetL2dot (rad/s^2('(,
Backlash
MATLAB Program (page 7)

54. 54
figure(2(
plot(T,thethm1d,'b-'(;
legend(labelBacklash,labelel(;
hold on;
plot(T,thethl1d,'r-.'(;
hold off;
title('Angular Rates of Motor and Load Versus Time'(,
%axis([0 1 -0.1 0.1[(,
grid, xlabel('Time (s('(, ylabel('ThetM1dot, NL*ThetL1dot (rad/s('(,
figure(3(
plot(T,thetm ,'b-'(;
legend(labelBacklash,labelel(;
hold on;
plot(T,thetl,'r-.'(;
hold off;
title('Angles of Motor and Load Versus Time'(,
%axis([0 5 -180 180[(,
grid, xlabel('Time (s('(, ylabel('Theta_Motor, NL*Theta_Load (deg('(,
figure(4(
plot(T,epsBLD ,'b-'(;
legend(labelBacklash,labelel(;
hold off;
title('Angle Errors EpsBL (deg( of Motor and Load Versus Time'(,
%axis([0 5 -180 180[(,
grid, xlabel('Time (s('(, ylabel('EpsBL (deg('(,
Backlash
MATLAB Program (page 8)

55. 55
figure(5(
plot(T,epsBLD ,'b-'(;
legend(labelBacklash,labelel(;
hold on;
plot(T,epsD,'r-.'(;
hold off;
title('Angle Errors EpsBL & Eps (deg( of Motor and Load Versus Time'(,
%axis([0 5 -180 180[(,
grid, xlabel('Time (s('(, ylabel('EpsBL, Eps (deg('(,
figure(6(
plot(T,epsdotBL,'b--'(;
legend(labelBacklash,labelel(;
hold off;
title('Rate of Angles of Errors (rad/s( Versus Time'(,
%axis([0 1 -0.1 0.1[(,
grid, xlabel('Time (s('(, ylabel('EpsDotBL (rad/s('(,
pause
Backlash
MATLAB Program (page 9)
Return to the Table of Content

56. 56
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
Rate of Angles of Errors (rad/s) Versus Time
Time
EpsDotBL
Backlash =0.01
el =0.9
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
0.05
0.06
Rate of Angles of Errors (rad/s) Versus Time
Time
EpsDotBL
Backlash =0.01
el =0.5
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0
0.01
0.02
0.03
0.04
0.05
0.06
Rate of Angles of Errors (rad/s) Versus Time
Time
EpsDotBL
Backlash =0.01
el =0
Simulation Results

57. 57
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
Rate of Angles of Errors (rad/s) Versus Time
Time
EpsDotBL
Backlash =0.01
el =0.9
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.1
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Angular Rates of Motor and Load Versus Time
Time
ThetM1dot,ThetL1dot Backlash =0.01
el =0.9
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
Rate of Angles of Errors (rad/s) Versus Time
Time
EpsDotBL
Backlash =0.01
el =0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.1
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Angular Rates of Motor and Load Versus Time
Time
ThetM1dot,ThetL1dot
Backlash =0.01
el =0
Return to the Table of Content

58. 58
SOLO Backlash
References
1.Donald T. Greenwood, “Principles of Dynamics”, Prentice Hall, 1965
2.Wolfram Stadler, “Analytical Robotics and Mechatronics”, McGraw-Hill, 1995
3.Hamilton H. Mabie and Fred W. Ocvirk, “Mechanism and Dynamics of
Machinery”, SI Version, Third Edition, John Wiley & Sons, 1978
4.Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas, “Mechanical
Engineering Design”, Seventh Edition, McGraw-Hill, 2004
Return to the Table of Content
5.Solo Hermelin, “Gears” Presentation, http://www.solohermelin.com

59. January 4, 2015 59
SOLO
Technion
Israeli Institute of Technology
1964 – 1968 BSc EE
1968 – 1971 MSc EE
Israeli Air Force
1970 – 1974
RAFAEL
Israeli Armament Development Authority
1974 – 2013
Stanford University
1983 – 1986 PhD AA