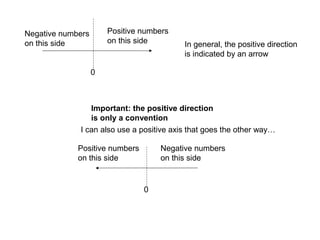
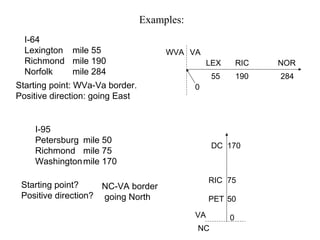
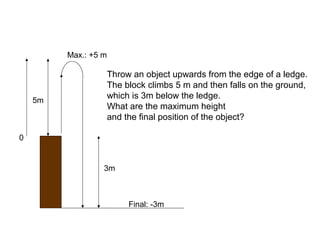
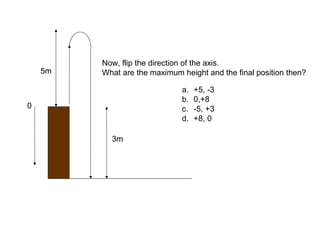
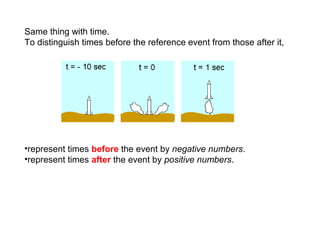
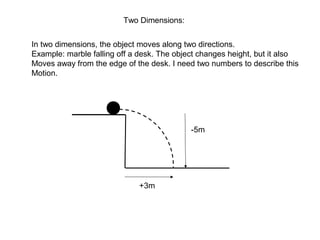
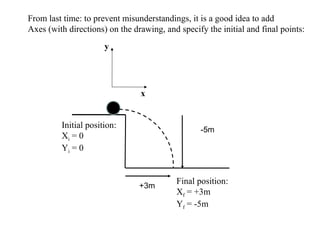
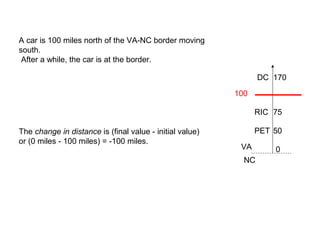
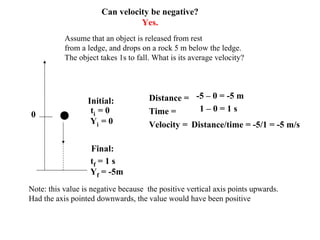
This document defines key concepts related to motion and velocity. It begins by defining the standard units of length, time, and mass used in physics. It then discusses the concepts of reference points, positive and negative directions, and representing positions as positive or negative numbers depending on their side of the reference point. The document also discusses using graphs to represent motion, defining maximum height and final position. It introduces the concepts of change, rate of change, and average velocity. It provides examples of calculating distance, change, time, and velocity for objects in motion. Finally, it demonstrates converting between units of velocity such as meters/second to kilometers/hour.

1. Describing motion
Once again, science in general and physics in particular
deals with simple systems.
Let’s start with really simple stuff:

2. Things move. I need to quantify movement.
First, I have to define units
Length: meter (m)
Time: second (s)
Mass: kilogram (kg)
Definitions are arbitrary, important is that everybody
uses the same units.
Also, I have to define a starting point, and a positive direction.

3. To distinguish positions on one side of a reference mark from
those on the other, represent distances.
•on one side by positive numbers.
•on the other side by negative numbers.

4. In general, the positive direction
is indicated by an arrow
0
Positive numbers
on this side
Negative numbers
on this side
Important: the positive direction
is only a convention
0
Positive numbers
on this side
Negative numbers
on this side
I can also use a positive axis that goes the other way…

5. I-64
Lexington mile 55
Richmond mile 190
Norfolk mile 284
Starting point: WVa-Va border.
Positive direction: going East
0
VAWVA
RIC NORLEX
55 190 284
Examples:
I-95
Petersburg mile 50
Richmond mile 75
Washingtonmile 170
Starting point?
Positive direction?
NC-VA border
going North
0VA
NC
RIC
DC
PET 50
170
75

6. Conclusion: the choice of the origin and of the positive direction does not
change the process.
Define Richmond as the starting point on I-64.
Where is Lexington?
Where is Norfolk?
-190
VAWVA
RIC NORLEX
-135 0 94
What has changed? The numbers.
Is Lexington still there? Yes, it did not move.
It is just at a negative distance from RIC.
Are the distances still the same? Yes.
Before: distance = RIC-LEX = 190-55 = 135 miles
Now: distance = RIC-LEX = 0-(-135) = 135 miles
The choice of the origin is also arbitrary…

7. Throw an object upwards from the edge of a ledge.
The block climbs 5 m and then falls on the ground,
which is 3m below the ledge.
What are the maximum height
and the final position of the object?
0
5m
Final: -3m
3m
Max.: +5 m

8. Now, flip the direction of the axis.
What are the maximum height and the final position then?
0
5m
3m
a. +5, -3
b. 0,+8
c. -5, +3
d. +8, 0

9. Same thing with time.
To distinguish times before the reference event from those after it,
•represent times before the event by negative numbers.
•represent times after the event by positive numbers.

10. The number of distances needed to fix the position of an object
is called the dimension of the motion.
In one dimension (e.g., cart moving on a straight road)
I need only one number to describe the motion.
That number is the distance covered by the object while moving along
The line.
The number will be positive if the object moves along the positive axis,
Negative if it moves opposite to the positive axis.

11. Two Dimensions:
-5m
+3m
In two dimensions, the object moves along two directions.
Example: marble falling off a desk. The object changes height, but it also
Moves away from the edge of the desk. I need two numbers to describe this
Motion.

12. x
y
-5m
+3m
From last time: to prevent misunderstandings, it is a good idea to add
Axes (with directions) on the drawing, and specify the initial and final points:
Initial position:
Xi = 0
Yi = 0
Final position:
Xf = +3m
Yf = -5m

13. Physics is about change.
The change in a quantity equals its final value minus its initial value.
The rate of change equals the change divided by the time taken.
The quantity Q can be anything: distance, money, velocity, field strength…

14. A car is on the VA-NC border moving north.
After a while, the car is 100 miles North of the border.
The change in distance is (final value - initial value)
or (100 miles - 0 miles) or 100 miles.
Example
0VA
NC
RIC
DC
PET 50
170
75
100

15. If the final value is smaller than the initial value,
then the change is a negative number.
Does it mean the change is not for real?
No. It means that the change is negative.
Example:
I pay $100 for a new Ipod.
Three months later, I resell it for $50.
What is the change?
∆Q = Qf – Qi = 50 – 100 = -50$

16. A car is 100 miles north of the VA-NC border moving
south.
After a while, the car is at the border.
The change in distance is (final value - initial value)
or (0 miles - 100 miles) = -100 miles.
0VA
NC
RIC
DC
PET 50
170
75
100

17. The average rate of change of a quantity is the change in the
quantity divided by the corresponding change in the time.

18. A car is on the VA-NC border moving north.
After one hour, the car is 100 miles North of the border.
The change in distance is (final value - initial value)
or (100 miles - 0 miles) or 100 miles.
The process took one hour, so the rate of change is
100/1 = 100 miles/hour
Example
0VA
NC
RIC
DC
PET 50
170
75
100

19. Velocity is the rate of change of position.
That is: How long it takes to get that far.
Example.
Last night I drove to Norfolk. It took me 2 hours to get there.
What was my average velocity?
• Distance traveled = final – initial = 284 – 190 = 94 miles
• Time traveled = final – initial = 2h – 0h = 2h
• Velocity = distance/time = 94 miles/2h = 47 miles/h
0
VAWVA
RIC NORLEX
55 190 284
First, let’s make a sketch…
t = 0 t = 2h
Do not forget: velocity = space/time
V = ∆s/∆t

20. Can velocity be negative?
Yes.
0
Yi = 0
Yf = -5m
ti = 0
tf = 1 s
Distance =
Time =
Velocity =
-5 – 0 = -5 m
1 – 0 = 1 s
Distance/time = -5/1 = -5 m/s
Initial:
Final:
Assume that an object is released from rest
from a ledge, and drops on a rock 5 m below the ledge.
The object takes 1s to fall. What is its average velocity?
Note: this value is negative because the positive vertical axis points upwards.
Had the axis pointed downwards, the value would have been positive

21. A runner moves along the positive x-direction and covers 100 m in 10 s.
What is its average velocity?
Xi = 0
ti = 0
Xf = 100
tf = 10
Distance = 100-0 = 100 m
Time = 10-0 = 10 s
Velocity = 100/10 = 10 m/s
Is this example realistic?

22. Unit conversion
So, man’s highest velocity is around 10 m/s.
How does that compare to a car?
Since the velocity of cars is usually measured in miles/hour, we
have to convert units.
How do we do this?
Let’s go first from m/s to km/h
How many m in one km? 1000. That is, I have to divide by 1000.
How many seconds in one hour? 3600. Divide by 3600.
h
km
h
kmx
hr
km
s
m
36
1000
360010
3600
1000
1
10
10 === ~ 22 miles/hour

23. Compare with other velocities:
Cheetah ~ 130 km/h
Elephant~ 40 km/h
Soccer (free kick) ~ 90-150 km/h
Tennis ball ~ 120 km/h
Revolution of earth around Sun ~ 107,000 km/h
Light ~ 300,000 km/s (second!)