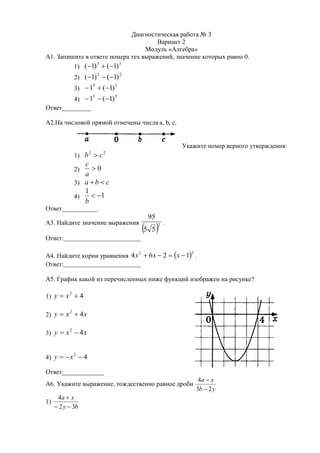
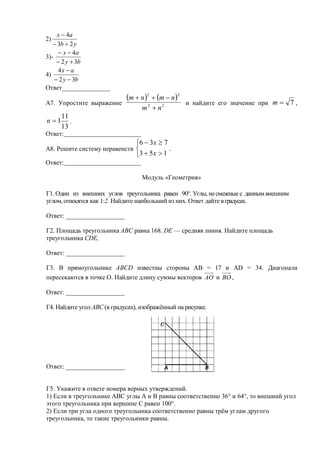
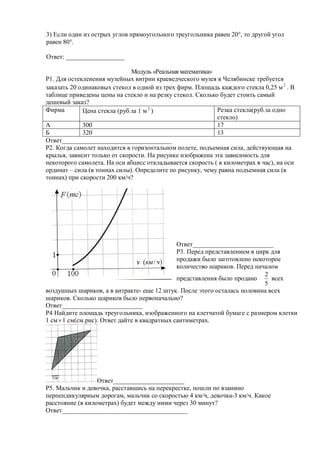
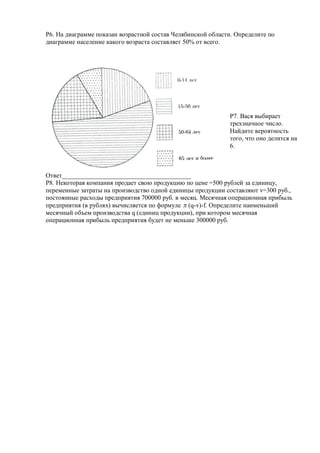
Документ содержит задания по алгебре, геометрии и реальной математике для учащихся, предлагая решить различные математические задачи, такие как нахождение корней уравнений, вычисление площадей и анализ графиков. Вопросы требуют применения знаний о числе, углах, площадях и вероятностях. Ответы следует записывать в указанных местах для каждой задачи.

1. Диагностическая работа № 3
Вариант 2
Модуль «Алгебра»
А1. Запишите в ответе номера тех выражений, значение которых равно 0.
3 3
1) (1)  (1)
2 2
2) (1)  (1)
5 3
3)  1  (1)
5 5
4)  1  (1)
Ответ_________
А2.На числовой прямой отмечены числа a, b, c.
Укажите номер верного утверждения:
2 2
1) b  c
c
2) 0
a
3) a  b  c
1
4)  1
b
Ответ___________
95
А3. Найдите значение выражения .
5 5  2
Ответ:
А4. Найдите корни уравнения 4 х  6 х  2   х  1 .
2 2
Ответ:
А5. График какой из перечисленных ниже функций изображен на рисунке?
2
1) у  х  4
2
2) у  х  4 х
2
3) у  х  4 х
2
4) у   х  4
Ответ_____________
4a  x
А6. Укажите выражение, тождественно равное дроби
3b  2 y
4a  x
1)
 2 y  3b

2. x  4a
2)
 3b  2 y
 x  4a
3)-
 2 y  3b
4x  a
4)
 2 y  3b
Ответ_______________
m  n 2  m  n 2
А7. Упростите выражение и найдите его значение при m  7,
m2  n2
11
n 1 .
13
Ответ:
6  3x  7
А8. Решите систему неравенств  .
3  5 x  1
Ответ:
Модуль «Геометрия»
Г1. Один из внешних углов треугольника равен 90°. Углы, не смежные с данным внешним
углом, относятся как 1:2. Найдите наибольший из них. Ответ дайте в градусах.
Ответ: __________________
Г2. Площадь треугольника ABC равна 168. DE — средняя линия. Найдите площадь
треугольника CDE,
Ответ: __________________
Г3. В прямоугольнике ABCD известны стороны AB = 17 и AD = 34. Диагонали
пересекаются в точке О. Найдите длину суммы векторов AO и BO ,
Ответ: __________________
Г4. Найдите угол АВС (в градусах), изображённый на рисунке.
Ответ: __________________
Г5. Укажите в ответе номера верных утверждений.
1) Если в треугольнике ABC углы А и В равны соответственно 36° и 64°, то внешний угол
этого треугольника при вершине С равен 100°.
2) Если три угла одного треугольника соответственно равны трём углам другого
треугольника, то такие треугольники равны.

3. 3) Если один из острых углов прямоугольного треугольника равен 20°, то другой угол
равен 80°.
Ответ: __________________
Модуль «Реальная математика»
Р1. Для остекленения музейных витрин краеведческого музея в Челябинске требуется
заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 м 2 . В
таблице приведены цены на стекло и на резку стекол. Сколько будет стоить самый
дешевый заказ?
Фирма Цена стекла (руб.за 1 м 2 ) Резка стекла(руб.за одно
стекло)
А 300 17
Б 320 13
Ответ__________________________________
Р2. Когда самолет находится в горизонтальном полете, подъемная сила, действующая на
крылья, зависит только от скорости. На рисунке изображена эта зависимость для
некоторого самолета. На оси абцисс откладывается скорость ( в километрах в час), на оси
ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в
тоннах) при скорости 200 км/ч?
Ответ_________________________
Р3. Перед представлением в цирк для
продажи было заготовлено некоторое
количество шариков. Перед началом
2
представления было продано всех
5
воздушных шариков, а в антракте- еще 12 штук. После этого осталась половина всех
шариков. Сколько шариков было первоначально?
Ответ_________________________
Р4 Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки
1 см  1 см(см.рис). Ответ дайте в квадратных сантиметрах.
Ответ______________________
Р5. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно
перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка-3 км/ч. Какое
расстояние (в километрах) будет между ними через 30 минут?
Ответ_______________________________________

4. Р6. На диаграмме показан возрастной состав Челябинской области. Определите по
диаграмме население какого возраста составляет 50% от всего.
Р7. Вася выбирает
трехзначное число.
Найдите вероятность
того, что оно делится на
6.
Ответ________________________________________
Р8. Некоторая компания продает свою продукцию по цене =500 рублей за единицу,
переменные затраты на производство одной единицы продукции составляют v=300 руб.,
постоянные расходы предприятия 700000 руб. в месяц. Месячная операционная прибыль
предприятия (в рублях) вычисляется по формуле  (q-v)-f. Определите наименьший
месячный объем производства q (единиц продукции), при котором месячная
операционная прибыль предприятия будет не меньше 300000 руб.