This document outlines the syllabus for the Physics component of the Malaysia Higher School Certificate Examination (STPM). It covers three terms: 1) The first term covers Mechanics and Thermodynamics, including physical quantities and units, kinematics, and dynamics. 2) The second term covers Electricity and Magnetism, including electrostatics, electric circuits, and electromagnetism. 3) The third term covers Oscillations and Waves, Optics, and Modern Physics, including wave motion, light, and quantum physics. The syllabus provides the topics, learning outcomes, examination format, and sample questions for the Physics course, which aims to enhance students' knowledge and

1. STPM/S(E)960
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
PEPERIKSAAN
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE EXAMINATION)
PHYSICS
Syllabus, Specimen Papers and Specimen Experiment
This syllabus applies for the 2012/2013 session and thereafter until further notice.

2. FALSAFAH PENDIDIKAN KEBANGSAAN
“Pendidikan di Malaysia adalah satu usaha berterusan
ke arah memperkembangkan lagi potensi individu secara
menyeluruh dan bersepadu untuk mewujudkan insan yang
seimbang dan harmonis dari segi intelek, rohani, emosi,
dan jasmani. Usaha ini adalah bagi melahirkan rakyat
Malaysia yang berilmu pengetahuan, berakhlak mulia,
bertanggungjawab, berketerampilan, dan berkeupayaan
mencapai kesejahteraan diri serta memberi sumbangan
terhadap keharmonian dan kemakmuran keluarga,
masyarakat dan negara.”

3. FOREWORD
This revised Physics syllabus is designed to replace the existing syllabus which has been in use since
the 2001 STPM examination. This new syllabus will be enforced in 2012 and the first examination
will also be held the same year. The revision of the syllabus takes into account the changes made by
the Malaysian Examinations Council (MEC) to the existing STPM examination. Through the new
system, sixth-form study will be divided into three terms, and candidates will sit for an examination at
the end of each term. The new syllabus fulfils the requirements of this new system. The main
objective of introducing the new examination system is to enhance the teaching and learning
orientation in sixth form so as to be in line with the orientation of teaching and learning in colleges
and universities.
The revision of the Physics syllabus incorporates current developments in physics studies and syllabus
design in Malaysia. The syllabus will give students exposure to pre-university level about Physics that
includes mechanics and thermodynamics, electricity and magnetism, oscillations and waves, optics,
and modern physics. The syllabus contains topics, teaching periods, learning outcomes, examination
format, grade description, and sample questions.
The design of this syllabus was undertaken by a committee chaired by Professor Dato’ Dr. Mohd.
Zambri bin Zainuddin from University of Malaya. Other committee members consist of university
lecturers, representatives from the Curriculum Development Division, Ministry of Education
Malaysia, and experienced teachers teaching Physics. On behalf of the MEC, I would like to thank the
committee for their commitment and invaluable contribution. It is hoped that this syllabus will be a
guide for teachers and candidates in the teaching and learning process.
OMAR BIN ABU BAKAR
Chief Executive
Malaysian Examinations Council

4. CONTENTS
Syllabus 960 Physics
Page
Aims 1
Objectives 1
Content
First Term: Mechanics and Thermodynamics 2–9
Second Term: Electricity and Magnetism 10 – 15
Third Term: Oscillations and Waves, Optics, and Modern Physics 16 – 22
Practical Syllabus (School-based Assessment of Practical (Paper 4)) 23 – 24
Written Practical Test (Paper 5) 24
Scheme of Assessment 25 – 26
Performance Descriptions 27
Summary of Key Quantities and Units 28 – 30
Values of constants 31
Reference Books 32
Specimen Paper 1 33 – 48
Specimen Paper 2 49 – 66
Specimen Paper 3 67 – 82
Specimen Experiment Paper 4 83 – 85
Specimen Paper 5 87 – 113

5. SYLLABUS
960 PHYSICS
Aims
This syllabus aims to enhance candidates’ knowledge and understanding of physics to enable them to
either further their studies at institutions of higher learning or assist them to embark on a related
career and also to promote awareness among them of the role of physics in the universe.
Objectives
The objectives of this syllabus are to enable candidates to:
(a) use models, concepts, principles, theories, and laws of physics;
(b) interpret and use scientific information presented in various forms;
(c) solve problems in various situations;
(d) analyse, synthesise, and evaluate information and ideas logically and critically;
(e) use techniques of operation and safety aspects of scientific equipment;
(f) plan and carry out experiments scientifically and make conclusions;
(g) develop proper attitudes, ethics, and values in the study and practice of physics.
1

6. FIRST TERM: MECHANICS AND THERMODYNAMICS
Teaching
Topic Learning Outcome
Period
1 Physical Quantities and 6 Candidates should be able to:
Units
1.1 Base quantities and 1 (a) list base quantities and their SI units:
SI units mass (kg), length (m), time (s), current (A),
temperature (K) and quantity of matter (mol);
(b) deduce units for derived quantities;
1.2 Dimensions of 1 (c) use dimensional analysis to determine the
physical quantities dimensions of derived quantities;
(d) check the homogeneity of equations using
dimensional analysis;
(e) construct empirical equations using
dimensional analysis;
1.3 Scalars and vectors 2 (f) determine the sum, the scalar product and
vector product of coplanar vectors;
(g) resolve a vector to two perpendicular
components;
1.4 Uncertainties in 2 (h) calculate the uncertainty in a derived quantity
measurements (a rigorous statistical treatment is not
required);
(i) write a derived quantity to an appropriate
number of significant figures.
2 Kinematics 6 Candidates should be able to:
2.1 Linear motion 2 (a) derive and use equations of motion with
constant acceleration;
(b) sketch and use the graphs of displacement-
time, velocity-time and acceleration-time for
the motion of a body with constant
acceleration;
2.2 Projectiles 4 (c) solve problems on projectile motion without
air resistance;
(d) explain the effects of air resistance on the
motion of bodies in air.
2

7. Teaching
Topic Learning Outcome
Period
3 Dynamics 12 Candidates should be able to:
3.1 Newton’s laws of 4 (a) state Newton’s laws of motion;
motion dv dm
(b) use the formula F = m +v for constant
dt dt
m or constant v only;
3.2 Linear momentum and 3 (c) state the principle of conservation of
its conservation momentum, and verify the principle using
Newton’s laws of motion;
(d) apply the principle of conservation of
momentum;
(e) define impulse as ∫F dt ;
(f) solve problems involving impulse;
3.3 Elastic and inelastic 2 (g) distinguish between elastic collisions and
collisions inelastic collisions (knowledge of coefficient
of restitution is not required);
(h) solve problems involving collisions between
particles in one dimension;
3.4 Centre of mass 1 (i) define centre of mass for a system of particles
in a plane;
(j) predict the path of the centre of mass of a two-
particle system;
3.5 Frictional forces 2 (k) explain the variation of frictional force with
sliding force;
(l) define and use coefficient of static function
and coefficient of kinetic friction.
4 Work, Energy and Power 5 Candidates should be able to:
4.1 Work 2 (a) define the work done by a force dW = F • ds ;
(b) calculate the work done using a force-
displacement graph;
(c) calculate the work done in certain situations,
including the work done in a spring;
4.2 Potential energy and 2 (d) derive and use the formula: potential energy
kinetic energy change = mgh near the surface of the Earth;
(e) derive and use the formula: kinetic energy
1
= mv 2 ;
2
3

8. Teaching
Topic Learning Outcome
Period
(f) state and use the work-energy theorem;
(g) apply the principle of conservation of energy
in situations involving kinetic energy and
potential energy;
4.3 Power 1 (h) derive and use the formula P = Fv ;
(i) use the concept of efficiency to solve
problems.
5 Circular Motion 8 Candidates should be able to:
5.1 Angular displacement 1 (a) express angular displacement in radians;
and angular velocity
(b) define angular velocity and period;
(c) derive and use the formula v = rω ;
5.2 Centripetal 2 (d) explain that uniform circular motion has an
acceleration acceleration due to the change in direction of
velocity;
(e) derive and use the formulae for centripetal
v2
acceleration a = and a = rω 2 ;
r
5.3 Centripetal force 5 (f) explain that uniform circular motion is due to
the action of a resultant force that is always
directed to the centre of the circle;
(g) use the formulae for centripetal force
mv 2
F= and F = mrω 2 ;
r
(h) solve problems involving uniform horizontal
circular motion for a point mass;
(i) solve problems involving vertical circular
motions for a point mass (knowledge of
tangential acceleration is not required).
6 Gravitation 10 Candidates should be able to:
6.1 Newton’s law of 1 (a) state Newton’s law of universal gravitation and
universal gravitation GMm
use the formula F = 2 ;
r
6.2 Gravitational field 2 (b) explain the meaning of gravitational field;
(c) define gravitational field strength as force of
gravity per unit mass;
4

9. Teaching
Topic Learning Outcome
Period
GM
(d) use the equation g = for a gravitational
r2
field;
6.3 Gravitational potential 3 (e) define the potential at a point in a gravitational
field;
GM
(f) derive and use the formula V = − ;
r
(g) use the formula for potential energy
GMm
U= − ;
r
(h) show that ΔU = mgΔr = mgh is a special case
GMm
of U = − for situations near to the
r
surface of the Earth;
dV
(i) use the relationship g = − ;
dr
(j) explain, with graphical illustrations, the
variations of gravitational field strength and
gravitational potential with distance from the
surface of the Earth;
6.4 Satellite motion in a 3 (k) solve problems involving satellites moving in
circular orbit a circular orbit in a gravitational field;
(l) explain the concept of weightlessness;
6.5 Escape velocity 1 (m) derive and use the equation for escape
2GM
velocity ve = and ve = 2 gR .
R
7 Statics 6 Candidates should be able to:
7.1 Centre of gravity 1 (a) define centre of gravity;
(b) state the condition in which the centre of mass
is the centre of gravity;
7.2 Equilibrium of 1 (c) state the condition for the equilibrium of a
particles particle;
(d) solve problems involving forces in equilibrium
at a point;
7.3 Equilibrium of rigid 4 (e) define torque as τ = r × F ;
bodies
(f) state the conditions for the equilibrium of a
rigid body;
5

10. Teaching
Topic Learning Outcome
Period
(g) sketch and label the forces which act on a
particle and a rigid body;
(h) use the triangle of forces to represent forces in
equilibrium;
(i) solve problems involving forces in
equilibrium.
8 Deformation of Solids 5 Candidates should be able to:
8.1 Stress and strain 1 (a) define stress and strain for a stretched wire or
elastic string;
8.2 Force-extension graph 2 (b) sketch force-extension graph and stress-strain
and stress-strain graph graph for a ductile material;
(c) identify and explain proportional limit, elastic
limit, yield point and tensile strength;
(d) define the Young’s modulus;
(e) solve problems involving Young’s modulus;
(f) distinguish between elastic deformation and
plastic deformation;
(g) distinguish the shapes of force-extension
graphs for ductile, brittle and polymeric
materials;
8.3 Strain energy 2 (h) derive and use the formula for strain energy;
(i) calculate strain energy from force-extension
graphs or stress-strain graphs.
9 Kinetic Theory of Gases 14 Candidates should be able to:
9.1 Ideal gas equation 2 (a) use the ideal gas equation pV = nRT ;
9.2 Pressure of a gas 2 (b) state the assumptions of the kinetic theory of
an ideal gas;
(c) derive and use the equation for the pressure
1
exerted by an ideal gas p = ρ c 2 ;
3
9.3 Molecular kinetic 2 (d) state and use the relationship between the
energy Boltzmann constant and molar gas constant
R
k= ;
NA
6

11. Teaching
Topic Learning Outcome
Period
(e) derive and use the expression for the mean
translational kinetic energy of a molecule,
1 3
mc 2 = kT ;
2 2
9.4 The r.m.s. speed of 2 (f) calculate the r.m.s. speed of gas molecules;
molecules
(g) sketch the molecular speed distribution graph
and explain the shape of the graph (description
of the experiment is not required);
(h) predict the variation of molecular speed
distribution with temperature;
9.5 Degrees of freedom 3 (i) define the degrees of freedom of a gas
and law of molecule;
equipartition of energy
(j) identify the number of degrees of freedom of a
monatomic, diatomic or polyatomic molecule
at room temperature;
(k) explain the variation in the number of degrees
of freedom of a diatomic molecule ranging
from very low to very high temperatures;
(l) state and apply the law of equipartition of
energy;
9.6 Internal energy of an 3 (m) distinguish between an ideal gas and a real gas;
ideal gas
(n) explain the concept of internal energy of an
ideal gas;
(o) derive and use the relationship between the
internal energy and the number of degrees of
freedom.
10 Thermodynamics of Gases 14 Candidates should be able to:
10.1 Heat capacities 2 (a) define heat capacity, specific heat capacity and
molar heat capacity;
(b) use the equations:
Q = CΔθ , Q = mcΔθ , Q = nCV,m Δθ and
Q = nCp,m Δθ ;
10.2 Work done by a gas 1 (c) derive and use the equation for work done by
a gas W = ∫ p dV ;
7

12. Teaching
Topic Learning Outcome
Period
10.3 First law of 5 (d) state and apply the first law of
thermodynamics thermodynamics Q = ΔU + W ;
(e) deduce the relationship ΔU = nCV, m ΔT from
the first law of thermodynamics;
(f) derive and use the equation Cp,m − CV,m = R ;
(g) relate CV,m and Cp,m to the degrees of
freedom;
Cp, m
(h) use the relationship γ = to identify the
CV, m
types of molecules;
10.4 Isothermal and 6 (i) describe the isothermal process of a gas;
adiabatic changes
(j) use the equation pV = constant for isothermal
changes;
(k) describe the adiabatic process of a gas;
(l) use the equations pV γ = constant and
TV γ −1 = constant for adiabatic changes;
(m) illustrate thermodynamic processes with p-V
graphs;
(n) derive and use the expression for work done in
the thermodynamic processes.
11 Heat Transfer 10 Candidates should be able to:
11.1 Conduction 5 (a) explain the mechanism of heat conduction
through solids, and hence, distinguish between
conduction through metals and non-metals;
(b) define thermal conductivity;
dQ dθ
(c) use the equation = − kA for heat
dt dx
conduction in one dimension;
(d) describe and calculate heat conduction through
a cross-sectional area of layers of different
materials;
(e) compare heat conduction through insulated
and non-insulated rods;
11.2 Convection 1 (f) describe heat transfer by convection;
(g) distinguish between natural and forced
convection;
8

13. Teaching
Topic Learning Outcome
Period
11.3 Radiation 3 (h) describe heat transfer by radiation;
dQ
(i) use Stefan-Boltzmann equation = eσ AT 4 ;
dt
(j) define a black body;
11.4 Global warming 1 (k) explain the greenhouse effect and thermal
pollution;
(l) suggest ways to reduce global warming.
9

14. SECOND TERM: ELECTRICITY AND MAGNETISM
Teaching
Topic Learning Outcome
Period
12 Electrostatics 12 Candidates should be able to:
12.1 Coulomb’s law 2 (a) state Coulomb’s law, and use the formula
Qq
F= ;
4π ε 0 r 2
12.2 Electric field 3 (b) explain the meaning of electric field, and
sketch the field pattern for an isolated point
charge, an electric dipole and a uniformly
charged surface;
(c) define the electric field strength, and use the
F
formula E = ;
q
(d) describe the motion of a point charge in a
uniform electric field;
12.3 Gauss’s law 4 (e) state Gauss’s law, and apply it to derive the
electric field strength for an isolated point
charge, an isolated charged conducting sphere
and a uniformly charged plate;
12.4 Electric potential 3 (f) define electric potential;
Q
(g) use the formula V = ;
4πε 0 r
(h) explain the meaning of equipotential surfaces;
dV
(i) use the relationship E = − ;
dr
(j) use the formula U = qV.
13 Capacitors 12 Candidates should be able to:
13.1 Capacitance 1 (a) define capacitance;
13.2 Parallel plate 2 (b) describe the mechanism of charging a parallel
capacitors plate capacitor;
Q ε A
(c) use the formula C = to derive C = 0 for
V d
the capacitance of a parallel plate capacitor;
10

15. Teaching
Topic Learning Outcome
Period
13.3 Dielectrics 2 (d) define relative permittivity ε r (dielectric
constant);
(e) describe the effect of a dielectric in a parallel
plate capacitor;
ε rε 0 A
(f) use the formula C = ;
d
13.4 Capacitors in series 2 (g) derive and use the formulae for effective
and in parallel capacitance of capacitors in series and in
parallel;
13.5 Energy stored in a 1 (h) use the formulae
charged capacitor 1 1 Q2 1
U= QV , U = and U = CV 2
2 2 C 2
(derivations are not required);
13.6 Charging and 4 (i) describe the charging and discharging process
discharging of a of a capacitor through a resistor;
capacitor
(j) define the time constant, and use the formula
τ = RC ;
(k) derive and use the formulae
⎛ −
t ⎞ ⎛ −
t ⎞
Q = Q0 ⎜1 − e τ ⎟ , V = V0 ⎜1 − e τ ⎟ and
⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
t
−
I = I 0 e τ for charging a capacitor through a
resistor;
t
−
(l) derive and use the formulae Q = Q0 e τ ,
t t
− −
V = V0 e τ and I = I 0 e τ for discharging a
capacitor through a resistor;
(m) solve problems involving charging and
discharging of a capacitor through a resistor.
14 Electric Current 10 Candidates should be able to:
14.1 Conduction of 2 (a) define electric current, and use the equation
electricity dQ
I= ;
dt
(b) explain the mechanism of conduction of
electricity in metals;
11

16. Teaching
Topic Learning Outcome
Period
14.2 Drift velocity 2 (c) explain the concept of drift velocity;
(d) derive and use the equation I = Anev ;
14.3 Current density 2 (e) define electric current density and
conductivity;
(f) use the relationship J = σ E ;
ne 2t
14.4 Electric conductivity 4 (g) derive and use the equation σ = ;
m
and resistivity
RA
(h) define resistivity, and use the formula ρ = ;
l
(i) show the equivalence between Ohm’s law and
the relationship J = σ E ;
(j) explain the dependence of resistivity on
temperature for metals and semiconductors by
ne 2t
using the equation σ = ;
m
(k) discuss the effects of temperature change on
the resistivity of conductors, semiconductors
and superconductors.
15 Direct Current Circuits 14 Candidates should be able to:
15.1 Internal resistance 1 (a) explain the effects of internal resistance on the
terminal potential difference of a battery in a
circuit;
15.2 Kirchhoff’s laws 4 (b) state and apply Kirchhoff’s laws;
15.3 Potential divider 2 (c) explain a potential divider as a source of
variable voltage;
(d) explain the uses of shunts and multipliers;
15.4 Potentiometer and 7 (e) explain the working principles of a
Wheatstone bridge potentiometer, and its uses;
(f) explain the working principles of a Wheatstone
bridge, and its uses;
(g) solve problems involving potentiometer and
Wheatstone bridge.
12

17. Teaching
Topic Learning Outcome
Period
16 Magnetic Fields 18 Candidates should be able to:
16.1 Concept of a magnetic 1 (a) explain magnetic field as a field of force
field produced by current-carrying conductors or by
permanent magnets;
16.2 Force on a moving 3 (b) use the formula for the force on a moving
charge charge F = qv × B ;
(c) use the equation F = qvB sin θ to define
magnetic flux density B;
(d) describe the motion of a charged particle
parallel and perpendicular to a uniform
magnetic field;
16.3 Force on a current- 3 (e) explain the existence of magnetic force on a
carrying conductor straight current-carrying conductor placed in a
uniform magnetic field;
(f) derive and use the equation F = IlB sin θ ;
16.4 Magnetic fields due to 4 (g) state Ampere’s law, and use it to derive the
currents μI
magnetic field of a straight wire B = 0 ;
2πr
μ 0 NI
(h) use the formulae B = for a circular coil
2r
and B = μ 0 nI for a solenoid;
16.5 Force between two 3 μ0 I1I 2l
current-carrying (i) derive and use the formula F = for the
2 πd
conductors force between two parallel current-carrying
conductors;
16.6 Determination of the 2 (j) describe the motion of a charged particle in the
e presence of both magnetic and electric fields
ratio
m (for v, B and E perpendicular to each other);
(k) explain the principles of the determination of
e
the ratio for electrons in Thomson’s
m
experiment (quantitative treatment is required);
16.7 Hall effect 2 (l) explain Hall effect, and derive an expression
for Hall voltage VH ;
(m) state the applications of Hall effect.
13

18. Teaching
Topic Learning Outcome
Period
17 Electromagnetic Induction 18 Candidates should be able to:
17.1 Magnetic flux 1 (a) define magnetic flux as Φ = B • A ;
17.2 Faraday’s law and 8 (b) state and use Faraday’s law and Lenz’s law;
Lenz’s law
(c) derive and use the equation for induced e.m.f.
in linear conductors and plane coils in uniform
magnetic fields;
17.3 Self induction 5 (d) explain the phenomenon of self-induction, and
define self-inductance;
dI
(e) use the formulae E = − L and LI = NΦ ;
dt
(f) derive and use the equation for the self-
μ N2A
inductance of a solenoid L = 0 ;
l
17.4 Energy stored in an 2 (g) use the formula for the energy stored in an
inductor 1
inductor U = LI 2 ;
2
17.5 Mutual induction 2 (h) explain the phenomenon of mutual induction,
and define mutual inductance;
(i) derive an expression for the mutual inductance
between two coaxial solenoids of the same
μ0 N p Ns A
cross-sectional area M = .
lp
18 Alternating Current 12 Candidates should be able to:
Circuits
18.1 Alternating current 3 (a) explain the concept of the r.m.s. value of an
through a resistor alternating current, and calculate its value for
the sinusoidal case only;
(b) derive an expression for the current from
V = V0 sin ωt ;
(c) explain the phase difference between the
current and voltage for a pure resistor;
(d) derive and use the formula for the power in an
alternating current circuit which consists only
of a pure resistor;
14

19. Teaching
Topic Learning Outcome
Period
18.2 Alternating current 3 (e) derive an expression for the current from
through an inductor V = V0 sin ωt ;
(f) explain the phase difference between the
current and voltage for a pure inductor;
(g) define the reactance of a pure inductor;
(h) use the formula X L = ω L ;
(i) derive and use the formula for the power in an
alternating current circuit which consists only
of a pure inductor;
18.3 Alternating current 3 (j) derive an expression for the current from
through a capacitor V = V0 sin ωt ;
(k) explain the phase difference between the
current and voltage for a pure capacitor;
(l) define the reactance of a pure capacitor;
1
(m) use the formula X C = ;
ωC
(n) derive and use the formula for the power in an
alternating current circuit which consists only
of a pure capacitor;
18.4 R-C and R-L circuits in 3 (o) define impedance;
series
(p) use the formula Z = R2 + ( X L − X C )2 ;
(q) sketch the phasor diagrams of R-C and R-L
circuits.
15

20. THIRD TERM: OSCILLATIONS AND WAVES, OPTICS, AND MODERN PHYSICS
Teaching
Topic Learning Outcome
Period
19 Oscillations 12 Candidates should be able to:
19.1 Characteristics of 1 (a) define simple harmonic motion;
simple harmonic
motion
19.2 Kinematics of simple 4 (b) show that x = A sin ωt is a solution of
harmonic motion a = −ω 2 x ;
(c) derive and use the formula v = ±ω A2 − x 2 ;
(d) describe, with graphical illustrations, the
variation in displacement, velocity and
acceleration with time;
(e) describe, with graphical illustrations, the
variation in velocity and acceleration with
displacement;
19.3 Energy in simple 2 (f) derive and use the expressions for kinetic
harmonic motion energy and potential energy;
(g) describe, with graphical illustrations, the
variation in kinetic energy and potential energy
with time and displacement;
19.4 Systems in simple 3 (h) derive and use expressions for the periods of
harmonic motion oscillations for spring-mass and simple
pendulum systems;
19.5 Damped oscillations 1 (i) describe the changes in amplitude and energy
for a damped oscillating system;
(j) distinguish between under damping, critical
damping and over damping;
19.6 Forced oscillations and 1 (k) distinguish between free oscillations and
resonance forced oscillations;
(l) state the conditions for resonance to occur.
20 Wave Motion 12 Candidates should be able to:
20.1 Progressive waves 3 (a) interpret and use the progressive wave
equation y = A sin (ω t − kx) or
y = A cos (ω t − kx);
(b) sketch and interpret the displacement-time
graph and the displacement-distance graph;
16

21. Teaching
Topic Learning Outcome
Period
2π x
(c) use the formula φ = ;
λ
(d) derive and use the relationship v = f λ ;
20.2 Wave intensity 2 (e) define intensity and use the relationship
I ∝ A2 ;
(f) describe the variation of intensity with distance
of a point source in space;
20.3 Principle of 1 (g) state the principle of superposition;
superposition
20.4 Standing waves 4 (h) use the principle of superposition to explain
the formation of standing waves;
(i) derive and interpret the standing wave
equation;
(j) distinguish between progressive and standing
waves;
20.5 Electromagnetic waves 2 (k) state that electromagnetic waves are made up
of electrical vibrations E = E0 sin (ω t − kx)
and magnetic vibrations B = B0 sin (ω t − kx);
(l) state the characteristics of electromagnetic
waves;
(m) compare electromagnetic waves with
mechanical waves;
1
(n) state the formula c = , and explain its
ε 0μ0
significance;
(o) state the orders of the magnitude of
wavelengths and frequencies for different
types of electromagnetic waves.
21 Sound Waves 14 Candidates should be able to:
21.1 Propagation of sound 2 (a) explain the propagation of sound waves in air
waves in terms of pressure variation and
displacement;
(b) interpret the equations for displacement
y = y0 sin (ω t − kx) and pressure
⎛ π⎞
p = p0 sin ⎜ ω t − kx + ⎟ ;
⎝ 2⎠
17

22. Teaching
Topic Learning Outcome
Period
(c) use the standing wave equation to determine
the positions of nodes and antinodes of a
standing wave along a stretched string;
21.2 Sources of sound 4 T
(d) use the formula v = to determine the
μ
frequencies of the sound produced by different
modes of vibration of the standing waves
along a stretched string;
(e) describe, with appropriate diagrams, the
different modes of vibration of standing waves
in air columns, and calculate the frequencies of
sound produced, including the determination
of end correction;
21.3 Intensity level of 2 (f) define and calculate the intensity level of
sound sound;
21.4 Beat 2 (g) use the principle of superposition to explain
the formation of beats;
(h) use the formula for beat frequency
f = f1 − f2 ;
21.5 Doppler effect 4 (i) describe the Doppler effect for sound, and use
the derived formulae (for source and/or
observer moving along the same line).
22 Geometrical Optics 8 Candidates should be able to:
r
22.1 Spherical mirrors 3 (a) use the relationship f = for spherical
2
mirrors;
(b) draw ray diagrams to show the formation of
images by concave mirrors and convex
mirrors;
1 1 1
(c) use the formula + = for spherical
u v f
mirrors;
22.2 Refraction at spherical 2 n1 n 2 n 2 − n1
surfaces (d) use the formula + = for
u v r
refraction at spherical surfaces;
18

23. Teaching
Topic Learning Outcome
Period
22.3 Thin lenses 3 n1 n 2 n 2 − n1
(e) use the formula + = to derive
u v r
1 1 1
the thin lens formula + = and
u v f
1 ⎛ nl ⎞⎛ 1 1 ⎞
lensmaker’s equation =⎜ − 1⎟⎜ − ⎟ ;
f m ⎝ nm ⎠⎝ r1 r2 ⎠
(f) use the thin lens formula and lensmaker’s
equation.
23 Wave Optics 16 Candidates should be able to:
23.1 Huygens’s principle 1 (a) state the Huygens’s principle;
(b) use the Huygens’s principle to explain
interference and diffraction phenomena;
23.2 Interference 2 (c) explain the concept of coherence;
(d) explain the concept of optical path difference,
and solve related problems;
(e) state the conditions for constructive and
destructive interferences;
23.3 Two-slit interference 2 (f) explain Young’s two-slit interference pattern;
pattern
λD
(g) derive and use the formula x = for the
a
fringe separation in Young’s interference
pattern;
23.4 Interference in a thin 2 (h) explain the phenomenon of thin film
film interference for normal incident light, and
solve related problems;
23.5 Diffraction by a single 2 (i) explain the diffraction pattern for a single slit;
slit
λ
(j) use the formula sin θ = for the first
a
minimum in the diffraction pattern for a single
slit;
λ
(k) use the formula sin θ = as the resolving
a
power of an aperture;
19

24. Teaching
Topic Learning Outcome
Period
23.6 Diffraction gratings 3 (l) explain the diffraction pattern for a diffraction
grating;
(m) use the formula d sin θ = mλ for a diffraction
grating;
(n) describe the use of a diffraction grating to form
the spectrum of white light, and to determine
the wavelength of monochromatic light;
23.7 Polarisation 2 (o) state that polarisation is a property of
transverse waves;
(p) explain the polarisation of light obtained by
reflection or using a polariser;
(q) use the Brewster’s law tan θ B = n ;
(r) use the Malus’s law I = I0 cos2 θ ;
23.8 Optical waveguides 2 (s) explain the basic principles of fibre optics and
waveguides;
(t) state the applications of fibre optics and
waveguides.
24 Quantum Physics 20 Students should be able to:
24.1 Photons 8 (a) describe the important observations in
photoelectric experiments;
(b) recognise the features of the photoelectric
effect that cannot be explained by wave theory,
and explain these features using the concept of
quantisation of light;
(c) use the equation E = hf for a photon;
(d) explain the meaning of work function and
threshold frequency;
(e) use Einstein’s equation for the photoelectric
1 2
effect hf = W + mvmax ;
2
(f) explain the meaning of stopping potential, and
1 2
use eVs = mvmax ;
2
20

25. Teaching
Topic Learning Outcome
Period
24.2 Wave-particle duality 2 (g) state de Broglie’s hypothesis;
h
(h) use the relation λ = to calculate de Broglie
p
wavelength;
(i) interpret the electron diffraction pattern as an
evidence of the wave nature of electrons;
(j) explain the advantages of an electron
microscope as compared to an optical
microscope;
24.3 Atomic structure 4 (k) state Bohr’s postulates for a hydrogen atom;
(l) derive an expression for the radii of the orbits
in Bohr’s model;
Z 2e4m
(m) derive the formula E n = − 2
for
8ε 0 h2n2
Bohr’s model;
(n) explain the production of emission line spectra
with reference to the transitions between
energy levels;
(o) explain the concepts of excitation energy and
ionisation energy;
24.4 X-rays 5 (p) interpret X-ray spectra obtained from X-ray
tubes;
(q) explain the characteristic line spectrum and
continuous spectrum including λ min in X-rays;
hc
(r) derive and use the equation λmin = ;
eV
(s) describe X-ray diffraction by two parallel
adjacent atomic planes;
(t) derive and use Bragg’s law 2d sin θ = mλ ;
24.5 Nanoscience 1 (u) explain the basic concept of nanoscience;
(v) state the applications of nanoscience in
electronics devices.
21

26. Teaching
Topic Learning Outcome
Period
25 Nuclear Physics 14 Candidates should be able to:
25.1 Nucleus 4 (a) describe the discovery of protons and neutrons
(experimental details are not required);
(b) explain mass defect and binding energy;
(c) use the formula for mass-energy equivalence
ΔE = Δmc2;
(d) relate and use the units u and eV;
(e) sketch and interpret a graph of binding energy
per nucleon against nucleon number;
25.2 Radioactivity 6 (f) explain radioactive decay as a spontaneous and
random process;
(g) define radioactive activity;
dN
(h) state and use the exponential law = −λN
dt
for radioactive decay;
(i) define decay constant;
(j) derive and use the formula N = N 0 e − λt ;
(k) define half-life, and derive the relation
ln 2
λ= ;
t1
2
(l) solve problems involving the applications of
radioisotopes as tracers in medical physics;
25.3 Nuclear reactions 4 (m) state and apply the conservation of nucleon
number and charge in nuclear reactions;
(n) apply the principle of mass-energy
conservation to calculate the energy released
(Q – value) in a nuclear reaction;
(o) relate the occurrence of fission and fusion
to the graph of binding energy per nucleon
against nucleon number;
(p) explain the conditions for a chain reaction to
occur;
(q) describe a controlled fission process in a
reactor;
(r) describe a nuclear fusion process which occurs
in the Sun.
22

27. The Practical Syllabus
School-based Assessment of Practical (Paper 4)
School-based assessment of practical work is carried out throughout the form six school terms for
candidates from government schools and private schools which have been approved by MEC to carry
out the school-based assessment.
MEC will determine 13 compulsory experiments and one project to be carried out by the
candidates and to be assessed by the subject teachers in schools in the respective terms. The project
will be carried out during the third term in groups of two or three candidates. Details of the title, topic,
objective, theory, apparatus and procedure of each of the experiments and project will be specified in
the Teacher’s and Student’s Manual for Practical Physics which can be downloaded from MEC Portal
(http://www.mpm.edu.my) during the first term of form six by the subject teachers.
Candidates should be supplied with a work scheme before the day of the compulsory experiment
so as to enable them to plan their practical work. Each experiment is expected to last one school
double period. Assessment of the practical work is done by the subject teachers during the practical
sessions and also based on the practical reports. The assessment should comply with the assessment
guidelines prepared by MEC.
A repeating candidate may use the total mark obtained in the coursework for two subsequent
examinations. Requests to carry forward the moderated coursework mark should be made during the
registration of the examination.
The Physics practical course for STPM should achieve its objective to improve the quality of
candidates in the aspects as listed below.
(a) The ability to follow a set or sequence of instructions.
(b) The ability to plan and carry out experiments using appropriate methods.
(c) The ability to choose suitable equipment and use them correctly and carefully.
(d) The ability to determine the best range of readings for more detailed and careful
measurements.
(e) The ability to make observations, to take measurements and to record data with attention
given to precision, accuracy and units.
(f) The awareness of the importance of check readings and repeat readings.
(g) The awareness of the limits of accuracy of observations and measurements.
(h) The ability to present data and information clearly in appropriate forms.
(i) The ability to interpret, analyse and evaluate observations, experimental data, perform error
analysis and make deductions.
(j) The ability to make conclusions.
(k) The awareness of the safety measures which need to be taken.
23

28. The objective of the project work is to enable candidates to acquire knowledge and integrate
practical skills in Physics with the aid of information and communications technology as well as to
develop soft skills as follows:
(a) communications,
(b) teamwork,
(c) critical thinking and problem solving,
(d) flexibility/adaptability,
(e) leadership,
(f) organising,
(g) information communications and technology,
(h) moral and ethics.
Written Practical Test (Paper 5)
The main objective of the written practical test is to assess the candidates’ understanding of practical
procedures in the laboratory.
The following candidates are required to register for this paper:
(a) individual private candidates,
(b) candidates from private schools which have no permission to carry out the school-based
assessment of practical work,
(c) candidates who repeat upper six (in government or private schools),
(d) candidates who do not attend classes of lower six and upper six in two consecutive years
(in government or private schools).
(e) candidates who take Physics other than the package offered by schools.
Three structured questions on routine practical work and/or design of experiments will be set.
MEC will not be strictly bound by the syllabus in setting questions. Where appropriate, candidates
will be given sufficient information to enable them to answer the questions. Only knowledge of theory
within the syllabus and knowledge of usual laboratory practical procedures will be expected.
The questions to be set will test candidates’ ability to:
(a) record readings from diagrams of apparatus,
(b) describe, explain, suggest, design or comment on experimental arrangements, techniques
and procedures,
(c) complete tables of data and plot graphs,
(d) interpret, draw conclusions from, and evaluate observations and experimental data,
(e) recognise limitations of experiments and sources of results,
(f) explain the effect of errors on experimental results,
(g) suggest precautions or safety measures,
(h) explain theoretical basis of experiments,
(i) use theory to explain or predict experimental results,
(j) perform simple calculations and error analysis based on experiments.
24

29. Scheme of Assessment
Term of Paper Code Mark
Theme/Title Type of Test Duration Administration
Study and Name (Weighting)
First 960/1 Mechanics and Written test 60
Term Physics Thermodynamics (26.67%)
Paper 1 Section A 15
15 compulsory
multiple-choice
questions to be
answered.
Section B 15
2 compulsory Central
1½ hours
structured questions assessment
to be answered.
Section C 30
2 questions to be
answered out of 3
essay questions.
All questions are
based on topics 1 to
11.
Second 960/2 Electricity and Written test 60
Term Physics Magnetism (26.67%)
Paper 2
Section A 15
15 compulsory
multiple-choice
questions to be
answered.
Section B 15
2 compulsory Central
1½ hours
structured questions assessment
to be answered.
Section C 30
2 questions to be
answered out of 3
essay questions.
All questions are
based on topics 12
to 18.
25

30. Term of Paper Code Mark
Theme/Title Type of Test Duration Administration
Study and Name (Weighting)
Third 960/3 Oscillations and Written test 60
Term Physics Waves, Optics (26.67%)
Paper 3 and Modern
Section A 15
Physics
15 compulsory
multiple-choice
questions to be
answered.
Section B 15
2 compulsory Central
1½ hours
structured questions assessment
to be answered.
Section C 30
2 questions to be
answered out of 3
essay questions.
All questions are
based on topics 19
to 25.
960/5 Written Physics Written practical 45
Physics Practical test (20%)
Paper 5 Central
1½ hours
3 compulsory assessment
structured questions
to be answered.
First, 960/4 Physics Practical School-based 225
Second Physics Assessment of To be
and Paper 4 Practical scaled to 45 Through
Third (20%) -out the School-based
13 compulsory
Terms three assessment
experiments and
terms
one project to be
carried out.
26

31. Performance Descriptions
A Grade A candidate is likely able to:
(a) recall the fundamental knowledge of Physics from the syllabus with few significant
omissions;
(b) show good understanding of the fundamental principles and concepts;
(c) identify the appropriate information and apply the correct techniques to solve problems;
(d) communicate effectively using logical sequence based on physics fundamentals, including
usage of mathematical expressions, schematic diagrams, tables and graph;
(e) synthesise information from fundamental principles of different content areas in problem
solving;
(f) show good understanding of the underlying working principles and carry out extensive
calculation in numerical-type questions;
(g) make adaptations, appropriate assumptions and use the fundamental knowledge of Physics
in analyzing an unfamiliar situation;
(h) identify causes, factors or errors in questions involving experiments;
(i) shows good knowledge relating precision of data to the accuracy of the final result;
(j) interpret and evaluate critically the numerical answer in calculations.
A Grade C candidate is likely able to:
(a) recall the knowledge of Physics from most parts of the syllabus;
(b) show some understanding of the main principles and concepts in the syllabus;
(c) present answer using common terminology and simple concepts in the syllabus;
(d) demonstrate some ability to link knowledge between different areas of Physics;
(e) perform calculation on familiar numerical-type or guided questions;
(f) show some understanding of the underlying Physics principles when carrying out numerical
work;
(g) identify causes, factors or errors in questions involving experiments;
(h) shows good knowledge relating precision of data to the accuracy of the final result;
(i) interpret and evaluate critically the numerical answer in calculations.
27

32. Summary of Key Quantities and Units
Candidates are expected to be familiar with the following quantities, their symbols, their units, and
their interrelationships. They should also be able to perform calculations and deal with questions
involving these quantities as indicated in the syllabus. The list should not be considered exhaustive.
Quantity Usual symbols Units
Base quantities
Amount of matter n mol
Electric current I A
Length l m
Mass m kg
Temperature T K
Time t s
Other quantities
Acceleration a m s−2
Acceleration of free fall g m s−2
Activity of radioactive source A s−1, Bq
Amplitude A m
Angular displacement
. θ °, rad
Angular frequency ω rad s−1
Angular momentum L kg m2 rad s−1
Angular speed ω, θ rad s−1
Angular velocity ω, θ rad s−1
Area A m2
Atomic mass ma kg
Atomic number (proton number) Z
Capacitance C F
Change of internal energy ΔU J
Charge carrier density n m−3
Coefficient of friction μ
Conductivity σ Ω−1m−1
Critical angle θc °
Current density J A m−2
Decay constant λ s−1
Density ρ kg m−3
Displacement s, x m
Distance d m
Electric charge Q, q C
Electric field strength E N C−1
Electric flux Φ N C−1 m2
Electric potential V V
Electric potential difference V, ΔV V
Electromotive force ε, E V
Electron mass me kg, u
Elementary charge e C
Emissivity e
Energy E, U J
Focal length f m
Force F N
28

33. Quantity Usual symbols Units
Force constant k N m−1
Frequency f Hz
Gravitational field strength g N kg−1
Gravitational potential V J kg−1
Half-life t½ s
Heat Q J
Heat capacity C J K−1
Image distance v m
Impedance Z Ω
Intensity I W m−2
Internal energy U J
Latent heat L J
Magnetic flux Φ Wb
Magnetic flux density B T
Magnification power m
Mass number (nucleon number) A
Mass per unit length μ kg m−1
Molar heat capacity Cm J K−1 mol−1
Molar mass M kg mol−1
Molecular speed c m s−1
Momentum p Ns
Mutual inductance M H
Neutron mass mn kg, u
Neutron number N
Object distance u m
Period T s
Permeability μ H m−1
Permeability of free space μ0 H m−1
Permittivity ε F m−1
Permittivity of free space ε0 F m−1
Phase difference φ °, rad
Potential energy U J
Power P W
Pressure p Pa
Principal molar heat capacities CV,m; Cp,m J K−1 mol−1
Radius r m
Ratio of heat capacities γ
Reactance X Ω
Refractive index n
Relative atomic mass Ar
Relative molecular mass Mr
Relative permeability μr
Relative permittivity εr
Resistance R Ω
Resistivity ρ Ωm
Self-inductance L H
Specific heat capacity c J K−1 kg−1
Specific latent heat l J kg−1
Speed u, v m s−1
Speed of electromagnetic waves c m s−1
29

34. Quantity Usual symbols Units
Stress σ Pa
Surface charge density σ C m−2
Temperature T, θ K, °C
Tension T N
Thermal conductivity k W m−1 K−1
Time constant τ s
Torque τ Nm
Velocity u, v m s−1
Volume V m3
Wavelength λ m
Wave number k m−1
Weight W N
Work W J
Work function φ, W J
Young’s modulus E, Y Pa, N m−2
30

35. 960 PHYSICS
Values of constants
Acceleration of free fall g = 9.81 m s−2
Avogadro’s constant NA = 6.02 × 1023 mol−1
Boltzmann’s constant k, kB = 1.38 × 10−23 J K−1
Gravitational constant G = 6.67 × 10−11 N m2 kg−2
Magnitude of electronic charge e = 1.60 × 10−19 C
Mass of the Earth ME = 5.97 × 1024 kg
Mass of the Sun MS = 1.99 × 1030 kg
Molar gas constant R = 8.31 J K−1 mol−1
Permeability of free space μ0 = 4π × 10−7 H m−1
Permittivity of free space ε0 = 8.85 × 10−12 F m−1
⎛ 1 ⎞ −9 −1
= ⎜ ⎟ × 10 F m
⎝ 36π ⎠
Planck’s constant h = 6.63 × 10−34 J s
Radius of the Earth RE = 6.38 × 106 m
Radius of the Sun RS = 6.96 × 108 m
Rest mass of electron me = 9.11 × 10−31 kg
Rest mass of proton mp = 1.67 × 10−27 kg
Speed of light in free space c = 3.00 × 108 m s−1
Stefan-Boltzmann constant σ = 5.67 × 10−8 W m−2 K−4
Unified atomic mass unit u = 1.66 × 10−27 kg
31

36. Reference Books
Teachers and candidates may use books specially written for the STPM examination and other
reference books such as those listed below.
1. Adam, S. and Allday, J., 2000. Advanced Physics. New York: Oxford.
2. Breithaupt, J., 2000. Understanding Physics for Advanced Level. 4th edition. Cheltenham:
Nelson Thornes.
3. Duncan, T., 2000. Advanced Physics. 5th edition. London: John Murray.
4. Giancoli, D.C., 2008. Physics for Scientists and Engineers with Modern Physics. 4th edition.
New Jersey: Pearson Prentice Hall.
5. Giancoli, D.C., 2008. Physics-Principles with Application. 6th edition. New Jersey: Pearson
Prentice Hall.
6. Halliday, D., Resnick, R., and Walker, J., 2008. Fundamentals of Physics. 8th edition. New
Jersey: John Wiley & Sons.
7. Hutchings, R., 2000. Physics. 2nd edition. London: Nelson Thornes.
8. Jewett Jr, J.W. and Serway, R.A., 2006. Serway’s Principles of Physics. 4th edition. California:
Thomson Brooks/Cole.
9. Jewett Jr, J.W. and Serway, R.A., 2008. Physics for Scientists and Engineers. 7th edition.
California: Thomson Brooks/Cole.
10. Nelkon, M. and Parker, P., 1995. Advanced Level Physics. 7th edition. Oxford: Heinemann.
11. Young, H.D. and Freedman, R.A., 2011. University Physics with Modern Physics. 13th edition.
California: Pearson Addison Wesley.
32

37. Identity card number:………………………….. Centre number/index number:……………………….
(Nombor kad pengenalan) (Nombor pusat/angka giliran)
SPECIMEN PAPER
960/1 STPM
PHYSICS (FIZIK)
PAPER 1 (KERTAS 1)
One and a half hours (Satu jam setengah)
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE)
Instructions to candidates:
DO NOT OPEN THIS QUESTION PAPER UNTIL YOU ARE TOLD TO DO SO.
Answer all questions in Section A. Marks will not be deducted for wrong answers. For each
question, four suggested answers are given. Choose the correct answer and circle the answer.
Answer all questions in Section B. Write your answers in the spaces provided.
Answer any two questions in Section C. All essential working should be shown. For numerical
answers, unit should be quoted wherever appropriate. Begin each answer on a fresh sheet of paper
and arrange your answers in numerical order.
Values of constants are provided on page in this question paper.
Arahan kepada calon:
JANGAN BUKA KERTAS SOALAN INI SEHINGGA ANDA DIBENARKAN BERBUAT
DEMIKIAN.
Jawab semua soalan dalam Bahagian A. Markah tidak akan ditolak bagi jawapan yang salah.
Bagi setiap soalan, empat cadangan jawapan diberikan. Pilih jawapan yang betul dan buat bulatan
pada jawapan tersebut.
Jawab semua soalan dalam Bahagian B. Tulis jawapan anda di ruang yang disediakan.
Jawab mana-mana dua soalan dalam Bahagian C. Semua jalan kerja yang sesuai hendaklah
ditunjukkan. Bagi jawapan berangka, unit hendaklah dinyatakan di mana-mana yang sesuai.
Mulakan setiap jawapan pada helaian kertas jawapan yang baharu dan susun jawapan anda
mengikut tertib berangka.
Nilai pemalar dibekalkan pada halaman kertas soalan ini.
This question paper consists of printed pages and blank page.
(Kertas soalan ini terdiri daripada halaman bercetak dan halaman kosong.)
© Majlis Peperiksaan Malaysia
STPM 960/1
33

38. Section A [15 marks]
Answer all questions in this section.
1 Which formula does not have the same unit as work?
A Power × time
B Pressure × volume
C Mass × gravitational potential
D Specific heat capacity × temperature
2 A ball is thrown upwards several times with the same speed at different angles of projection.
Which graph shows the variation of the horizontal range R with the angle of projection θ ?
C D
3 A body with mass 6 kg is acted by a force F which varies with time t as shown in the graph
below.
F/N
10
0 T t/s
If the change of the momentum of the body after time T is 30 N s, what is the value of T ?
A 3s B 5s C 6s D 12 s
960/1
34

39. Bahagian A [15 markah]
Jawab semua soalan dalam bahagian ini.
1 Rumus yang manakah yang tidak mempunyai unit yang sama dengan kerja?
A Kuasa × masa
B Tekanan × isi padu
C Jisim × keupayaan graviti
D Muatan haba tentu × suhu
2 Sebiji bola dilontarkan ke atas beberapa kali dengan laju yang sama pada sudut pelontaran yang
berbeza. Graf yang manakah yang menunjukkan ubahan julat mengufuk R dengan sudut pelontaran
θ?
C D
3 Satu jasad dengan jisim 6 kg ditindakkan oleh satu daya F yang berubah dengan masa t
ditunjukkan dalam graf di bawah.
F/N
10
0 T t/s
Jika perubahan momentum jasad itu selepas masa T ialah 30 N s, berapakah nilai T ?
A 3s B 5s C 6s D 12 s
960/1
35

40. 4 Which statement is true of the static friction between two surfaces?
A It is always constant.
B It depends on the surface area.
C It depends on the nature of the surfaces.
D It is always smaller than the kinetic friction.
5 A car of mass m with effective power P and initial velocity u climbs a hill of height h. The car
arrives at the peak of the hill at velocity v in time t. Which is true of the motion?
1 2 1 2
A Pt + mu = mv + mgh
2 2
1 2 1
B Pt + mv = mu 2 + mgh
2 2
1 1
C Pt + mgh = mu 2 − mv 2
2 2
1 2 1
D Pt + mgh = mv − mu 2
2 2
6 A car of mass 1000 kg moves along the corner of a level road having a radius of curvature 35.0 m.
If the limiting frictional force between the tyres and the road is 4.0 kN, the maximum speed of the car
without skidding at the corner is
A 4.0 m s−1 B 8.8 m s−1 C 11.8 m s−1 D 140.0 m s−1
7 If the gravitational field strength at a certain region is uniform,
A there is no work done on a mass displaced in that region
B the gravitational potential is the same at all points in that region
C the gravitational force on a mass is the same at all points in that region
D the gravitational potential energy is the same for all masses at all points in that region
8 A ladder PQ with the centre of mass R resting on a wall QS is shown in the diagram below.
T
Q
R
U
P S
If the ladder is in equilibrium and the resultant forces at P and Q are FP and FQ respectively, FP
and FQ must act through point
A R B S C T D U
960/1
36

41. 4 Penyataan yang manakah yang benar tentang geseran statik antara dua permukaan?
A Ia sentiasa malar.
B Ia bergantung kepada luas permukaan itu.
C Ia bergantung kepada sifat permukaan itu.
D Ia sentiasa lebih kecil daripada geseran kinetik.
5 Sebuah kereta berjisim m dengan kuasa berkesan P dan halaju awal u mendaki sebuah bukit
setinggi h. Kereta itu tiba di puncak bukit pada halaju v dalam masa t. Yang manakah yang benar
tentang gerakan itu?
1 1
A Pt + mu 2 = mv 2 + mgh
2 2
1 2 1
B Pt + mv = mu 2 + mgh
2 2
1 1
C Pt + mgh = mu 2 − mv 2
2 2
1 1
D Pt + mgh = mv 2 − mu 2
2 2
6 Sebuah kereta berjisim 1000 kg bergerak melalui satu selekoh jalan raya yang rata yang
mempunyai jejari kelengkungan 35.0 m. Jika had daya geseran antara tayar dengan jalan raya ialah
4.0 kN, laju maksimum tanpa tergelincir kereta pada selekoh itu ialah
A 4.0 m s−1 B 8.8 m s−1 C 11.8 m s−1 D 140.0 m s−1
7 Jika kekuatan medan graviti di suatu kawasan adalah seragam,
A tiada kerja dilakukan ke atas jisim yang tersesar di kawasan itu
B keupayaan graviti adalah sama di semua titik di kawasan itu
C daya graviti ke atas jisim adalah sama di semua titik di kawasan itu
D tenaga keupayaan graviti adalah sama bagi semua jisim di semua titik di kawasan itu
8 Satu tangga PQ dengan pusat jisim R yang bersandar pada dinding QS ditunjukkan dalam gambar
rajah di bawah.
T
Q
R
U
P S
Jika tangga itu berada dalam keseimbangan dan daya paduan di P dan Q masing-masing ialah FP
dan FQ, FP dan FQ mesti bertindak melalui titik
A R B S C T D U
960/1
37

42. 9 Which of the following best shows the stiffness of a solid?
A Young’s modulus
B Elastic limit
C Yield point
D Tensile strength
10 The temperature of two moles of a diatomic gas is raised by 8.0 °C from room temperature. The
increase in the internal energy of the gas is
A 2.0 × 102 J B 3.3 × 102 J C 7.0 × 103 J D 1.2 × 104 J
11 The ratio of the molar heat capacity of an ideal gas is 1.4. What is the number of degrees of
freedom of the gas?
A 3 B 5 C 6 D 7
12 Molar heat capacity at constant pressure differs from molar heat capacity at constant volume
because
A the internal energy of the gas is higher at constant pressure
B extra heat is required to expand the gas at constant pressure
C extra heat is required to increase the degree of freedom of the gas at constant volume
D work is required to overcome the attractive force between molecules which is stronger at
constant pressure
13 An ideal gas in a cylinder is compressed isothermally. Which statement is true of the gas?
A No work is done on the gas.
B Heat is released from the gas.
C The internal energy of the gas increases.
D The potential energy of the gas molecules increases.
960/1
38

43. 9 Yang manakah yang paling baik menunjukkan kekakuan suatu pepejal?
A Modulus Young’s
B Had kenyal
C Titik alah
D Kekuatan tegangan
10 Suhu dua mol gas dwiatom dinaikkan sebanyak 8.0 °C dari suhu bilik. Pertambahan tenaga dalam
bagi gas itu ialah
A 2.0 × 102 J B 3.3 × 102 J C 7.0 × 103 J D 1.2 × 104 J
11 Nisbah muatan haba molar suatu gas unggul ialah 1.4. Berapakah bilangan darjah kebebasan gas
itu?
A 3 B 5 C 6 D 7
12 Muatan haba molar pada tekanan malar berbeza daripada muatan haba molar pada isi padu molar
kerana
A tenaga dalam suatu gas adalah lebih tinggi pada tekanan malar
B haba tambahan diperlukan untuk mengembangkan gas pada tekanan malar
C haba tambahan diperlukan untuk meningkatkan darjah kebebasan gas pada isi padu malar
D kerja diperlukan untuk mengatasi daya tarikan antara molekul yang lebih kuat pada tekanan
malar
13 Suatu gas unggul dalam satu silinder dimampatkan secara isoterma. Penyataan yang manakah
yang benar tentang gas itu?
A Tiada kerja dilakukan ke atas gas.
B Haba dibebaskan daripada gas.
C Tenaga dalam gas itu meningkat.
D Tenaga keupayaan molekul gas meningkat.
960/1
39

44. 14 Two perfectly insulated uniform rods R and S of the same material joined thermally is shown in
the diagram below.
Insulator
100 °C R S 50 °C
Insulator
The length of rod R is two times the length of rod S. The cross-sectional area of rod R is half the
cross-sectional area of rod S. If the free ends of R and S are fixed at 100 °C and 50 °C respectively,
what is the temperature at the junction of rod R and rod S?
A 55 °C B 60 °C C 75 °C D 90 °C
15 The Sun continuously radiates energy into space, some of which is received by the Earth. The
average temperature on the surface of the Earth remains at about 300 K because
A the Earth reflects the Sun’s light
B the thermal conductivity of the Earth is low
C the Earth radiates an amount of energy into space equal to the amount it absorbed
D the energy only raises the temperature of the upper atmosphere and never reaches the
surface
960/1
40

45. 14 Dua rod seragam R dan S yang bertebat dengan sempurna daripada bahan yang sama disambung
secara terma ditunjukkan dalam gambar rajah di bawah.
Penebat
100 °C R S 50 °C
Penebat
Panjang rod R adalah dua kali panjang rod S. Luas keratan rentas rod R adalah setengah luas
keratan rentas rod S. Jika hujung bebas R dan S masing-masing ditetapkan pada 100 °C and 50 °C,
berapakah suhu pada simpang rod R dan rod S?
A 55 °C B 60 °C C 75 °C D 90 °C
15 Matahari secara berterusan menyinarkan tenaga ke dalam angkasa, sebahagian daripadanya
diterima oleh Bumi. Purata suhu pada permukaan Bumi kekal pada 300 K kerana
A Bumi memantulkan cahaya Matahari
B kekonduksian terma Bumi adalah rendah
C Bumi menyinarkan amaun tenaga yang sama dengan amaun tenaga yang diserapnya ke dalam
angkasa
D tenaga hanya meningkatkan suhu atmosfera atas dan tidak pernah sampai ke permukaan
960/1
41

46. Section B [15 marks]
Answer all questions in this section.
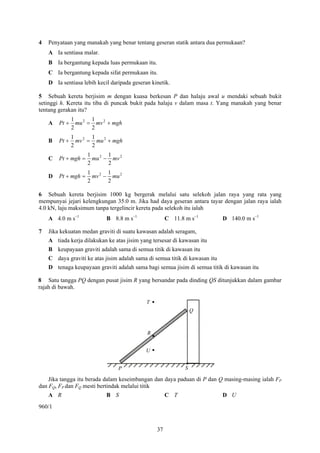
16 A wire with cross-sectional area 0.50 mm2 and length 20.0 cm is pulled at both ends by a force of
55 N as shown in the diagram below.
F = 55 N Wire F = 55 N
(a) Determine the stress in the wire. [2 marks]
(b) If the extension is 0.40 cm, calculate the strain in the wire. [2 marks]
(c) Determine the Young’s modulus of the wire. [2 marks]
(d) Calculate the strain energy stored in the wire. [2 marks]
17 (a) State two assumptions of an ideal gas. [2 marks]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
(b) State two physical conditions under which a gas behave as an ideal gas. [2 marks]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
(c) A 0.035 m3 gas tank contains 7.0 kg of butane gas. Assuming that the gas behaves as an ideal
gas, calculate its pressure at 27 °C. [3 marks]
[The molecular mass of butane is 58 g mol–1.]
960/1
42

47. Bahagian B [15 markah]
Jawab semua soalan dalam bahagian ini.
16 Satu dawai dengan luas kerata rentas 0.50 mm2 dan panjang 20.0 cm ditarik di kedua-dua hujung
oleh satu daya 55 N seperti ditunjukkan dalam gambar rajah di bawah.
F = 55 N Dawai F = 55 N
(a) Tentukan tegasan dalam dawai itu. [2 markah]
(b) Jika pemanjangan ialah 0.40 cm, hitung terikan dalam dawai itu. [2 markah]
(c) Tentukan modulus Young dawai itu. [2 markah]
(d) Hitung tenaga terikan yang tersimpan dalam dawai itu. [2 markah]
17 (a) Nyatakan dua anggapan suatu gas unggul. [2 markah]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
(b) Nyatakan dua syarat fizikal yang mana satu gas bertindak sebagai satu gas unggul.
[2 markah]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
(c) Sebuah tangki gas 0.035 m3 mengandungi 7.0 kg gas butana. Andaikan bahawa gas itu
bertindak sebagai satu gas unggul, hitung tekanannya pada 27 °C. [3 markah]
[Jisim molekul butana ialah 58 g mol–1.]
960/1
43

48. Section C [30 marks]
Answer any two questions in this section.
18 (a) (i) State the principle of conservation of linear momentum. [2 marks]
(ii) In a perfect elastic collision, the total kinetic energy is conserved. Discuss a case where
the total kinetic energy is lost completely after a collision between two objects. [2 marks]
(b) An object of mass M is moving with velocity u, and collides elastically with another object of
mass m at rest. After the collision, M and m move with velocities v1 and v2 respectively.
(i) Write the equations to show the conservation of the kinetic energy and the conservation
of the linear momentum. [2 marks]
(ii) Using the equations in (b)(i), obtain a relationship between u, v1 and v2. [3 marks]
(iii) Determine the condition required for the object of mass M to stop after the collision.
[3 marks]
(iv) If M = 40.0 g, m = 60.0 g and u = 8.0 m s–1, calculate the percentage change in kinetic
energy of the object of mass M after the collision. [3 marks]
19 (a) (i) State Newton’s law of universal gravitation. [2 marks]
(ii) Explain why the force of gravity of the Earth on an object causes the object to
accelerate towards the Earth. [2 marks]
(b) The weight of a satellite in a circular orbit around the Earth is half of its weight on the surface
of the Earth. The mass of the satellite is 8.0 × 102 kg.
(i) Determine the altitude of the orbit. [3 marks]
(ii) Determine the speed of the satellite. [2 marks]
(iii) Determine the minimum energy required by the satellite to escape from its orbit to
space. [3 marks]
(iv) If the satellite is replaced with another satellite of mass 1.6 × 103 kg, state the effect on
your answers for (i), (ii) and (iii). . [3 marks]
960/1
44

49. Bahagian C [30 markah]
Jawab mana-mana dua soalan dalam bahagian ini.
18 (a) (i) Nyatakan prinsip keabadian momentum linear. [2 markah]
(ii) Dalam satu perlanggaran elastik yang sempurna, jumlah tenaga kinetik diabadikan.
Bincangkan satu kes dengan jumlah tenaga kinetik hilang sepenuhnya selepas perlanggaran antara dua
objek. [2 markah]
(b) Satu objek berjisim M bergerak dengan halaju u, dan berlanggar secara elastik dengan objek
lain berjisim m yang berada dalam keadaan rehat. Selepas perlanggaran, M dan m bergerak masing-
masing dengan halaju v1 dan v2.
(i) Tuliskan persamaan untuk menunjukkan keabadian tenaga kinetik dan keabadian
momentum linear. [2 markah]
(ii) Dengan menggunakan persamaan dalam (b)(i), dapatkan satu perhubungan antara u, v1,
dan v2. [3 markah]
(iii) Tentukan syarat yang diperlukan bagi objek berjisim M itu untuk berhenti selepas
perlanggaran. [3 markah]
(iv) Jika M = 40.0 g, m = 60.0 g, dan u = 8.0 m s–1, hitung peratusan perubahan tenaga
kinetik objek berjisim M itu selepas perlanggaran. [3 markah]
19 (a) (i) Nyatakan hukum kegravitian semesta Newton. [2 markah]
(ii) Jelaskan mengapa daya graviti Bumi pada satu objek menyebabkan objek itu memecut
ke arah Bumi. [2 markah]
(b) Berat satu satelit dalam satu orbit bulat yang mengelilingi Bumi ialah setengah daripada
beratnya pada permukaan Bumi. Jisim satelit itu ialah 8.0 × 102 kg.
(i) Tentukan altitud orbit itu. [3 markah]
(ii) Tentukan laju satelit itu. [2 markah]
(iii) Tentukan tenaga minimum yang diperlukan oleh satelit untuk terlepas dari orbitnya ke
angkasa. [3 markah]
(iv) Jika satelit itu digantikan dengan satelit yang lain berjisim 1.6 × 103 kg, nyatakan kesan
pada jawapan anda dalam (i), (ii), dan (iii). [3 markah]
960/1
45

50. 20 (a) (i) State the first law of thermodynamics. [2 marks]
(ii) Using the first law of thermodynamics, explain the changes due to the work done in an
isothermal expansion and an adiabatic expansion for an ideal gas. [5 marks]
(b) A pump which is used to compress air into a big tank is shown in the diagram below.
To tank Valve Piston
0.300 m
Initially the air in the pump is at atmospheric pressure 1.01 × 105 Pa and temperature 300 K. The
pump has a uniform cylindrical space of length 0.300 m, and the valve opens when the air in the pump
exceeds a pressure of 6.25 × 105 Pa. Assuming that the compression is adiabatic and that the air
behaves as a diatomic ideal gas,
(i) determine the distance for which the piston moves before the air starts to enter the tank,
[4 marks]
(ii) determine the temperature of the compressed air, [2 marks]
(iii) determine the work done by the pump to fill 50.0 mol of air into the tank. [2 marks]
960/1
46

51. 20 (a) (i) Nyatakan hukum termodinamik pertama. [2 markah]
(ii) Dengan menggunakan hukum termodinamik pertama, jelaskan perubahan yang
disebabkan oleh kerja yang dilakukan dalam pengembangan isoterma dan pengembangan adiabatik
bagi satu gas unggul. [5 markah]
(b) Satu pam yang digunakan untuk memampatkan udara ke dalam satu tangki besar ditunjukkan
dalam gambar rajah di bawah.
Ke tangki Injap Piston
0.300 m
Pada awalnya udara di dalam pam ialah pada tekanan atmosfera 1.01 × 105 Pa dan suhu 300 K.
Pam itu mempunyai ruang silinder yang seragam dengan panjang 0.300 m, dan injap terbuka apabila
udara di dalam pam melebihi tekanan 6.25 × 105 Pa. Andaikan bahawa mampatan itu ialah mampatan
adiabatik dan udaranya bertindak sebagai satu gas unggul dwiatom,
(i) tentukan jarak pada ketika piston bergerak sebelum udara mula memasuki tangki,
[4 markah]
(ii) tentukan suhu udara yang termampat, [2 markah]
(iii) tentukan kerja yang dilakukan oleh pam untuk memenuhkan 50.0 mol udara ke dalam
tangki itu. [2 markah]
960/1
47

52. Values of constants
(Nilai Pemalar)
Acceleration of free fall (Pecutan jatuh bebas) g = 9.81 m s−2
Avogadro constant (Pemalar Avogadro) NA = 6.02 × 1023 mol−1
Boltzmann constant (Pemalar Boltzmann) k, kB = 1.38 × 10−23 J K−1
Gravitational constant (Pemalar graviti) G = 6.67 × 10−11 N m2 kg−2
Magnitude of electronic (Magnitud cas elektron) e = 1.60 × 10−19 C
charge
Mass of the Earth (Jisim Bumi) ME = 5.97 × 1024 kg
Mass of the Sun (Jisim Matahari) MS = 1.99 × 1030 kg
Molar gas constant (Pemalar gas molar) R = 8.31 J K−1 mol−1
Permeability of free space (Ketelapan ruang bebas) μ0 = 4π × 10−7 H m−1
Permittivity of free space (Ketelusan ruang bebas) ε0 = 8.85 × 10−12 F m−1
= ⎛ 1 ⎞ −9 −1
⎜ ⎟ × 10 F m
⎝ 36π ⎠
Planck’s constant (Pemalar Planck) h = 6.63 × 10−34 J s
Radius of the Earth (Jejari Bumi) RE = 6.38 × 106 m
Radius of the Sun (Jejari Matahari) RS = 6.96 × 108 m
Rest mass of electron (Jisim rehat elektron) me = 9.11 × 10−31 kg
Rest mass of proton (Jisim rehat proton) mp = 1.67 × 10−27 kg
Speed of light in free space (Laju cahaya dalam ruang bebas) c = 3.00 × 108 m s−1
Stefan-Boltzmann constant (Pemalar Stefan-Boltzmann) σ = 5.67 × 10−8 W m−2 K−4
Unified atomic mass unit (Unit jisim atom bersatu) u = 1.66 × 10−27 kg
960/1
48

53. Identity card number:………………………….. Centre number/index number:……………………….
(Nombor kad pengenalan) (Nombor pusat/angka giliran)
SPECIMEN PAPER
960/2 STPM
PHYSICS (FIZIK)
PAPER 2 (KERTAS 2)
One and a half hours (Satu jam setengah)
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE)
Instructions to candidates:
DO NOT OPEN THIS QUESTION PAPER UNTIL YOU ARE TOLD TO DO SO.
Answer all questions in Section A. Marks will not be deducted for wrong answers. For each
question, four suggested answers are given. Choose the correct answer and circle the answer.
Answer all questions in Section B. Write your answers in the spaces provided.
Answer any two questions in Section C. All essential working should be shown. For numerical
answers, unit should be quoted wherever appropriate. Begin each answer on a fresh sheet of paper
and arrange your answers in numerical order.
Values of constants are provided on page in this question paper.
Arahan kepada calon:
JANGAN BUKA KERTAS SOALAN INI SEHINGGA ANDA DIBENARKAN BERBUAT
DEMIKIAN.
Jawab semua soalan dalam Bahagian A. Markah tidak akan ditolak bagi jawapan yang salah.
Bagi setiap soalan, empat cadangan jawapan diberikan. Pilih jawapan yang betul dan buat bulatan
pada jawapan tersebut.
Jawab semua soalan dalam Bahagian B. Tulis jawapan anda di ruang yang disediakan.
Jawab mana-mana dua soalan dalam Bahagian C. Semua jalan kerja yang sesuai hendaklah
ditunjukkan. Bagi jawapan berangka, unit hendaklah dinyatakan di mana-mana yang sesuai.
Mulakan setiap jawapan pada helaian kertas jawapan yang baharu dan susun jawapan anda
mengikut tertib berangka.
Nilai pemalar dibekalkan pada halaman kertas soalan ini.
This question paper consists of printed pages and blank page.
(Kertas soalan ini terdiri daripada halaman bercetak dan halaman kosong.)
© Majlis Peperiksaan Malaysia
STPM 960/2
49

54. Section A [15 marks]
Answer all questions in this section.
1 A Gaussian surface encloses a charge of 2.0 μC in vacuum. What is the electric flux through the
surface?
A 1.8 × 10−17 V m
B 4.4 × 10−6 V m
C 1.8 × 104 V m
D 2.3 × 105 V m
2 Which statement is not true of an isolated charged conducting sphere?
A Electric field exists inside the conductor.
B The potential in the conductor is constant.
C The charge distribution on the conductor is uniform.
D The charge is distributed only on the surface of the conductor.
3 The space between the plates of a parallel-plate capacitor needs to be completely filled by a
dielectric material to increase its capacitance. Which will give the highest capacitance?
Dielectric material Permittivity Thickness
A Teflon 2ε0 0.4 mm
B Quartz 3ε0 0.8 mm
C Glass 4ε0 1.0 mm
D Mica 5ε0 1.2 mm
960/2
50

55. Bahagian A [15 markah]
Jawab semua soalan dalam bahagian ini.
1 Satu permukaan Gauss mengurungi cas 2.0 μC dalam vakum. Berapakah fluks elektrik menerusi
permukaan itu?
A 1.8 × 10−17 V m
B 4.4 × 10−6 V m
C 1.8 × 104 V m
D 2.3 × 105 V m
2 Penyataan yang manakah yang tidak benar tentang cas terpencil sfera pengkonduksi?
A Medan elektrik wujud di dalam konduktor.
B Keupayaan di dalam konduktor adalah malar.
C Taburan cas pada konduktor adalah seragam.
D Cas ditaburkan hanya pada permukaan konduktor.
3 Ruang di antara plat-plat satu kapasitor plat selari perlu dipenuhkan selengkapnya dengan bahan
dielektrik untuk meningkatkan nilai kapasitans. Yang manakah yang akan memberikan kapasitans
yang paling tinggi?
Bahan dielektrik Ketelusan Ketebalan
A Teflon 2ε0 0.4 mm
B Kuartz 3ε0 0.8 mm
C Kaca 4ε0 1.0 mm
D Mika 5ε0 1.2 mm
960/2
51

56. 4 A switch S connected to terminal 1 at time t = 0 is shown in the circuit diagram below.
S
When the voltmeter reading has reached V0 at time t = T, the switch S is flipped to terminal 2.
Which graph shows the correct variation of voltmeter reading V with time t?
5 The equation which relates the electrical conductivity σ of the material of a conductor with other
ne 2t
quantities is σ = , where n, e and m are symbols with the usual meaning. t in the equation
m
represents
A the thickness of the conductor
B the mean distance between adjacent atoms in the conductor
C the mean time between the collisions of free electrons with lattice ions
D the mean time for a free electron to move from one end to the other end of the conductor
960/2
52

57. 4 Satu suis S yang disambungkan ke terminal 1 pada masa t = 0 ditunjukkan dalam gambar rajah
litar di bawah.
S
Apabila bacaan voltmeter telah mencapai V0 pada masa t = T, suis S ditukar ke terminal 2. Graf
yang manakah yang menunjukkan dengan betul ubahan bacaan voltmeter V dengan masa t?
5 Persamaan yang mengaitkan kekonduksian elektrik σ bahan suatu konduktor dengan kuantiti-
ne 2t
kuantiti lain ialah σ = , dengan n, e, dan m adalah simbol yang membawa makna yang biasa. t
m
dalam persamaan itu mewakili
A ketebalan konduktor itu
B min jarak antara atom-atom bersebelahan dalam konduktor itu
C min masa antara perlanggaran elektron bebas dengan ion kekisi
D min masa bagi satu elektron bebas untuk bergerak dari satu hujung konduktor ke hujung yang
lain
960/2
53

58. 6 When a potential difference V is applied across two ends of a copper wire with diameter d and
d L
length L, the drift velocity of the electrons is v. If a copper wire of diameter and length with
2 4
potential difference of 2V applied across the two ends, the drift velocity, in terms of v, is
A v B 2v C 4v D 8v
7 A cell of e.m.f. ε connected to three identical bulbs R, S and T and a rheostat XY is shown in the
circuit diagram below.
X
P
S
ε
Y
T
R
If the contact P of the rheostat is adjusted towards Y, which statement is true of the changes in the
brightness of the three bulbs?
A R, S and T become brighter.
B R and T become brighter, but S becomes dimmer.
C R becomes brighter, but S and T become dimmer.
D R and S become brighter, but T becomes dimmer.
8 A potentiometer with a 100 cm wire XY is shown in the circuit diagram below.
P
X Y
K
E is a dry cell of e.m.f. 1.5 V and internal resistance 0.50 Ω. R is a resistor of 2.0 Ω. When switch
K is open, the balance point P from X is 75 cm. When switch K is closed, the new balance point from
X is
A 30 cm B 40 cm C 60 cm D 75 cm
960/2
54

59. 6 Apabila beza keupayaan V dikenakan merentas dua hujung satu dawai kuprum dengan garis pusat
d
d dan panjang L, halaju hanyut elektron ialah v. Jika satu dawai kuprum bergaris pusat dan panjang
2
L
dengan beza keupayaan 2V dikenakan merentas dua hujung, halaju hanyut, dalam sebutan v, ialah
4
A v B 2v C 4v D 8v
7 Satu sel dengan d.g.e ε disambungkan ke tiga mentol R, S, dan T yang seiras dan satu reostat XY
ditunjukkan dalam gambar rajah litar di bawah.
X
P
S
ε
Y
T
R
Jika sesentuh P reostat dilaraskan ke arah Y, penyataan yang manakah yang benar tentang
perubahan kecerahan tiga mentol itu?
A R, S, dan T menjadi lebih cerah.
B R dan T menjadi lebih cerah, tetapi S menjadi malap.
C R menjadi lebih cerah, tetapi S dan T menjadi malap.
D R dan S menjadi lebih cerah, tetapi T menjadi malap.
8 Satu potentiometer dengan 100 cm dawai XY ditunjukkan dalam gambar rajah litar di bawah.
P
X Y
K
E ialah sel kering dengan d.g.e. 1.5 V dan rintangan dalam 0.50 Ω. R ialah perintang 2.0 Ω.
Apabila suis K dibuka, titik seimbang P daripada X ialah 75 cm. Apabila suis K ditutup, titik
seimbang daripada X yang baharu ialah
A 30 cm B 40 cm C 60 cm D 75 cm
960/2
55

60. 9 An electron moves into a uniform magnetic field with a certain velocity. If the velocity of the
electron is in the same direction as the magnetic field,
A the electron accelerates
B the electron decelerates
C the electron continues to move with its original velocity
D the electron is deflected and moves in a circle at constant speed
10 Four parallel wires passing through the four vertices of a square WXYZ is shown in the diagram
below.
W M X
P O Q
Z N Y
These wires carry currents of equal magnitude in the directions shown. The resultant magnetic
field at the centre O of the square is in the direction of
A OM B ON C OP D OQ
11 Which statement is true of Hall effect?
A The Hall voltage for ordinary metal is a few volts.
B Hall effect can be used to determine the type of charge carrier.
C The Hall voltage is not dependent on the dimensions of the material.
D The electric force by the Hall voltage on the charge carriers exceeds the magnetic force.
12 A circular coil is placed in a uniform magnetic field. Which quantity does not influence the
magnitude of the charge flow in the coil when the coil is pulled out from the magnetic field?
A Area of the coil
B Resistance of the coil
C Magnetic flux density
D The time taken to pull the coil out from the magnetic field
960/2
56

61. 9 Satu elektron bergerak masuk ke dalam medan magnet seragam dengan satu halaju tertentu. Jika
halaju elektron itu adalah searah dengan medan magnet,
A elektron itu memecut
B elektron itu nyahpecutan
C elektron itu terus bergerak dengan halaju asal
D elektron itu dipesongkan dan bergerak dalam satu bulatan dengan laju malar
10 Empat dawai selari yang melalui empat bucu satu segi empat sama WXYZ ditunjukkan dalam
gambar rajah di bawah.
W M X
O
P Q
Z N Y
Dawai-dawai ini membawa arus yang sama magnitudnya mengikut arah yang ditunjukkan.
Medan magnet paduan di pusat O segi empat itu ialah dalam arah
A OM B ON C OP D OQ
11 Penyataan yang manakah yang benar tentang kesan Hall?
A Voltan Hall pada logam biasa ialah beberapa volt.
B Kesan Hall dapat digunakan untuk menentukan jenis pembawa cas.
C Voltan Hall tidak bergantung pada dimensi sesuatu bahan.
D Daya elektrik oleh voltan Hall pada pembawa cas melebihi daya magnet.
12 Satu gegelung bulat diletakkan dalam medan magnet seragam. Kuantiti yang manakah yang tidak
mempengaruhi magnitud aliran cas dalam gegelung apabila gegelung itu ditarik keluar dari medan
magnet?
A Luas gegelung
B Rintangan gegelung
C Ketumpatan fluks magnet
D Masa yang diambil untuk menarik gegelung keluar dari medan magnet
960/2
57

62. P
13 The mutual inductance M between two coils is defined by M = − . What do P and Q represent?
Q
P Q
A E.m.f. induced in primary coil Rate of change of current in secondary coil
B E.m.f. induced in secondary coil Rate of change of current in primary coil
C Potential difference across primary coil Potential difference across secondary coil
D Potential difference across secondary coil Potential difference across primary coil
14 An alternating current I which flows through a 5 Ω resistor is given by I = 2 sin (50t), where I is
in amperes and t in seconds. The mean power dissipated in the resistor is
A 5W B 10 W C 20 W D 50 W
15 An R-C circuit is shown in the diagram below.
R C
The r.m.s. voltage across R and C are 10 V and 7 V respectively. What is the r.m.s. voltage of the
source?
A 3V B 12 V C 17 V D 24 V
960/2
58

63. P
13 Induktan saling M antara dua gegelung ditakrifkan sebagai M = − . Apakah yang mewakili P
Q
dan Q?
P Q
A D.g.e. teraruh dalam gegelung primer Kadar perubahan arus dalam gegelung
sekunder
B D.g.e. teraruh dalam gegelung sekunder Kadar perubahan arus dalam gegelung
primer
C Beza keupayaan merentas gegelung primer Beza keupayaan merentas gegelung
sekunder
D Beza keupayaan merentas gegelung sekunder Beza keupayaan merentas gegelung primer
14 Arus ulang-alik I yang mengalir melalui satu perintang 5 Ω diberikan sebagai I = 2 sin (50t),
dengan I dalam ampere dan t dalam saat. Min kuasa yang terlesap dalam perintang ialah
A 5W B 10 W C 20 W D 50 W
15 Satu litar R-C ditunjukkan dalam gambar rajah di bawah.
R C
Voltan p.m.k.d. merentas R dan C ialah masing-masing 10 V dan 7 V. Berapakah voltan p.m.k.d.
sumber itu?
A 3V B 12 V C 17 V D 24 V
960/2
59

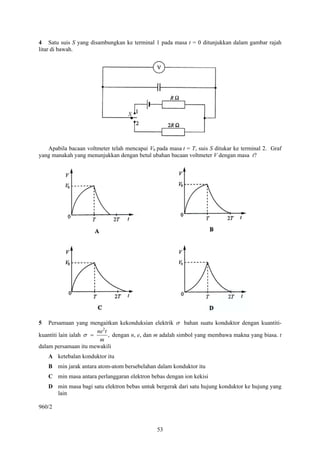
64. Section B [15 marks]
Answer all questions in this section.
16 Two thin conducting plates have an area of 0.50 m2 each. They are placed parallel to each other
and 25 mm apart. One plate is maintained at +75 V while the other at –75 V by a d.c. supply.
(a) Define capacitance of a capacitor. [1 mark]
……………………………………………………………………………………………………………
(b) Determine the amount of charge stored on each plate. [4 marks]
(c) Calculate the energy stored in the electric field between the plates. [2 marks]
17 (a) State Kirchhoff’s laws. [2 marks]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
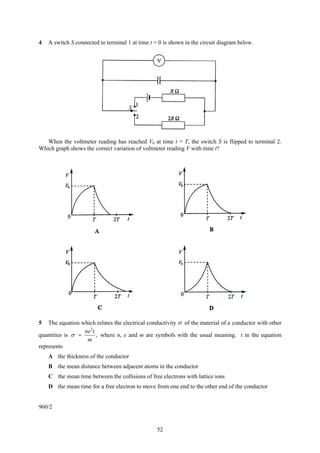
(b) Cell X of e.m.f. 3.0 V with internal resistance 1.0 Ω and cell Y of e.m.f. 3.0 V with internal
resistance 2.0 Ω are connected as shown in the circuit diagram below.
X Y
I2 I I1
5.0 Ω 3.0 Ω
P Q
(i) Calculate current I1 and I2. [4 marks]
(ii) Determine the potential different between P and Q. [2 marks]
960/2
60

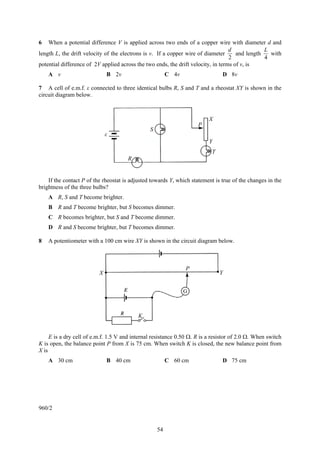
65. Bahagian B [15 markah]
Jawab semua soalan dalam bahagian ini.
16 Dua plat pengkonduksi nipis tiap-tiap satu mempunyai luas 0.50 m2. Plat-plat itu diletakkan selari
antara satu sama lain dan terpisah sejauh 25 mm. Satu plat dikekalkan pada +75 V manakala plat
yang satu lagi pada –75 V oleh satu bekalan a.t.
(a) Takrifkan kapasitans satu kapasitor. [1 markah]
……………………………………………………………………………………………………………
(b) Tentukan amaun cas yang tersimpan pada setiap plat. [4 markah]
(c) Hitung tenaga yang tersimpan dalam medan elektrik di antara plat-plat itu. [2 markah]
17 (a) Nyatakan hukum Kirchhoff. [2 markah]
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
(b) Sel X mempunyai d.g.e. 3.0 V dengan rintangan dalam 1.0 Ω dan sel Y mempunyai d.g.e.
3.0 V dengan rintangan dalam 2.0 Ω disambungkan seperti ditunjukkan dalam gambar rajah litar
di bawah.
X Y
I2 I I1
5.0 Ω 3.0 Ω
P Q
(i) Hitung arus I1 dan I2. [4 markah]
(ii) Tentukan beza keupayaan antara P dengan Q. [2 markah]
960/2
61

66. Section C [30 marks]
Answer any two questions in this section.
18 (a) Two fixed spherical conductors X and Y which is separated by a distance of 0.50 m is shown
in the diagram below.
+3.0 μC –2.0 μC
X Y
0.50 m
Conductor X has a radius 0.15 cm and charge +3.0 μC. Conductor Y has a radius of 0.30 cm and
charge –0.20 μC.
(i) Calculate the force between the two spheres. [3 marks]
(ii) The two spheres are then connected with a thin wire. The wire is then removed from
the spheres. Calculate the charge on each sphere. [5 marks]
(b) (i) Using Gauss’s law, explain why a person inside a hollow metallic sphere of radius R
maintained at a high electric potential does not experience an electric shock. [4 marks]
(ii) Sketch a graph of electric field E against distance r for r < R and r > R for the situation
in (b)(i). [4 marks]
19 (a) Explain microscopically why
(i) metal becomes hot when an electric current flows through it, [2 marks]
(ii) the resistivity of a metal increases while the resistivity of a semiconductor decreases
when the temperature rises. [4 marks]
(b) A current of 5.0 A flows in a wire of length 1.50 m and cross-sectional area 1.2 mm2. The
potential difference is 6.0 V.
(i) Determine the power dissipated in the wire. [3 marks]
(ii) Determine the drift velocity of free electrons if the electron density is
1.5 × 1028 m–3. [3 marks]
(iii) Calculate the force experienced by a free electron if all the power dissipated in the wire
is used to drift the free electrons. [3 marks]
960/2
62

67. Bahagian C [30 markah]
Jawab mana-mana dua soalan dalam bahagian ini.
18 (a) Dua konduktor sfera yang ditetapkan X dan Y yang dipisahkan oleh satu jarak 0.50 m
ditunjukkan dalam gambar rajah di bawah.
+3.0 μC –2.0 μC
X Y
0.50 m
Konduktor X mempunyai jejari 0.15 cm dan cas +3.0 μC. Konduktor Y mempunyai jejari 0.30
cm dan cas –0.20 μC.
(i) Hitung daya di antara dua sfera itu. [3 markah]
(ii) Dua sfera itu kemudiannya dihubungkan dengan satu dawai nipis. Dawai itu
kemudiannya ditanggalkan dari sfera-sfera itu. Hitung cas pada setiap sfera. [5 markah]
(b) (i) Dengan menggunakan hukum Gauss, jelaskan mengapa seseorang di dalam satu sfera
logam lompang berjejari R dikekalkan pada suatu keupayaan elektrik yang tinggi tidak mengalami
renjatan elektrik. [4 markah]
(ii) Lakar satu graf medan elektrik E lawan jarak r untuk r < R dan r > R bagi situasi dalam
(b)(i). [4 markah]
19 (a) Jelaskan secara mikroskopik mengapa
(i) logam menjadi panas apabila arus elektrik mengalir melaluinya, [2 markah]
(ii) kerintangan satu logam bertambah manakala kerintangan satu semikonduktor berkurang
apabila suhu meningkat. [4 markah]
(b) Satu arus 5.0 A mengalir dalam satu dawai yang panjang 1.50 m dan luas keratan rentas
1.2 mm2. Beza keupayaan ialah 6.0 V.
(i) Tentukan kuasa terlesap dalam dawai itu. [3 markah]
(ii) Tentukan halaju hanyut elektron bebas jika ketumpatan elektron ialah 1.5 × 1028 m–3.
[3 markah]
(iii) Hitung daya yang dialami oleh satu elektron bebas jika semua kuasa yang terlesap
dalam dawai itu digunakan untuk menghanyutkan elektron bebas itu. [3 markah]
960/2
63

68. 20 (a) (i) Define magnetic flux density, and state its unit. [3 marks]
(ii) State two differences between the force due to electric field and the force due to
magnetic field on a charged particle. [2 marks]
(iii) State Ampere’s law, and use it to derive the magnetic field of a long straight wire.
[4 marks]
(b) A long fixed horizontal wire PQ carries current 80.0 A in the direction QP as shown in the
diagram below.
P Q
80.0A 80.0A
String 0.15m
R S
A copper wire RS of diameter 0.40 mm having the same length of PQ hanging horizontally
0.15 m below PQ on two light strings. An e.m.f. source is connected across terminals R and S. If the
density of copper is 8930 kg m−3, determine the minimum current and its direction needed to flow
through RS so that the tension in the strings is zero. [6 marks]
960/2
64

69. 20 (a) (i) Takrifkan ketumpatan magnetik fluks, dan nyatakan unitnya. [3 markah]
(ii) Nyatakan dua perbezaan antara daya yang disebabkan oleh medan elektrik dengan daya
yang disebabkan oleh medan magnet pada satu zarah bercas. [2 markah]
(iii) Nyatakan hukum Ampere, dan gunakan hukum Ampere untuk terbitkan medan magnet
satu dawai lurus yang panjang. [4 markah]
(b) Satu dawai panjang mengufuk yang tetap PQ membawa arus 80.0 A dalam arah QP seperti
ditunjukkan dalam gambar rajah di bawah.
P Q
80.0 A 80.0 A
Tali 0.15m
R S
Satu dawai kuprum RS bergaris pusat 0.40 mm mempunyai panjang yang sama dengan PQ
tergantung secara mengufuk 0.15 m di bawah PQ pada dua tali ringan. Satu sumber d.g.e. disambung
merentas terminal R dan S. Jika ketumpatan kuprum ialah 8930 kg m−3, tentukan arus minimum dan
arah yang diperlukannya untuk mengalir melalui RS supaya tegangan dalam tali adalah sifar.
[6 markah]
960/2
65

70. Values of constants
(Nilai Pemalar)
Acceleration of free fall (Pecutan jatuh bebas) g = 9.81 m s−2
Avogadro constant (Pemalar Avogadro) NA = 6.02 × 1023 mol−1
Boltzmann constant (Pemalar Boltzmann) k, kB = 1.38 × 10−23 J K−1
Gravitational constant (Pemalar graviti) G = 6.67 × 10−11 N m2 kg−2
Magnitude of electronic (Magnitud cas elektron) e = 1.60 × 10−19 C
charge
Mass of the Earth (Jisim Bumi) ME = 5.97 × 1024 kg
Mass of the Sun (Jisim Matahari) MS = 1.99 × 1030 kg
Molar gas constant (Pemalar gas molar) R = 8.31 J K−1 mol−1
Permeability of free space (Ketelapan ruang bebas) μ0 = 4π × 10−7 H m−1
Permittivity of free space (Ketelusan ruang bebas) ε0 = 8.85 × 10−12 F m−1
= ⎛ 1 ⎞ −9 −1
⎜ ⎟ × 10 F m
⎝ 36π ⎠
Planck’s constant (Pemalar Planck) h = 6.63 × 10−34 J s
Radius of the Earth (Jejari Bumi) RE = 6.38 × 106 m
Radius of the Sun (Jejari Matahari) RS = 6.96 × 108 m
Rest mass of electron (Jisim rehat elektron) me = 9.11 × 10−31 kg
Rest mass of proton (Jisim rehat proton) mp = 1.67 × 10−27 kg
Speed of light in free space (Laju cahaya dalam ruang bebas) c = 3.00 × 108 m s−1
Stefan-Boltzmann constant (Pemalar Stefan-Boltzmann) σ = 5.67 × 10−8 W m−2 K−4
Unified atomic mass unit (Unit jisim atom bersatu) u = 1.66 × 10−27 kg
960/2
66

71. Identity card number:………………………….. Centre number/index number:……………………….
(Nombor kad pengenalan) (Nombor pusat/angka giliran)
SPECIMEN PAPER
960/3 STPM
PHYSICS (FIZIK)
PAPER 3 (KERTAS 3)
One and a half hours (Satu jam setengah)
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE)
Instructions to candidates:
DO NOT OPEN THIS QUESTION PAPER UNTIL YOU ARE TOLD TO DO SO.
Answer all questions in Section A. Marks will not be deducted for wrong answers. For each
question, four suggested answers are given. Choose the correct answer and circle the answer.
Answer all questions in Section B. Write your answers in the spaces provided.
Answer any two questions in Section C. All essential working should be shown. For numerical
answers, unit should be quoted wherever appropriate. Begin each answer on a fresh sheet of paper
and arrange your answers in numerical order.
Values of constants are provided on page in this question paper.
Arahan kepada calon:
JANGAN BUKA KERTAS SOALAN INI SEHINGGA ANDA DIBENARKAN BERBUAT
DEMIKIAN.
Jawab semua soalan dalam Bahagian A. Markah tidak akan ditolak bagi jawapan yang salah.
Bagi setiap soalan, empat cadangan jawapan diberikan. Pilih jawapan yang betul dan buat bulatan
pada jawapan tersebut.
Jawab semua soalan dalam Bahagian B. Tulis jawapan anda di ruang yang disediakan.
Jawab mana-mana dua soalan dalam Bahagian C. Semua jalan kerja yang sesuai hendaklah
ditunjukkan. Bagi jawapan berangka, unit hendaklah dinyatakan di mana-mana yang sesuai.
Mulakan setiap jawapan pada helaian kertas jawapan yang baharu dan susun jawapan anda
mengikut tertib berangka.
Nilai pemalar dibekalkan pada halaman kertas soalan ini.
This question paper consists of printed pages and blank page.
(Kertas soalan ini terdiri daripada halaman bercetak dan halaman kosong.)
© Majlis Peperiksaan Malaysia
STPM 960/3
67

72. Section A [15 marks]
Answer all questions in this section.
1 A particle of mass m performs a simple harmonic motion with amplitude A and frequency f. The
total energy of this simple harmonic motion is
1
A mA2f 2
B 2mA2f 2
C 2π2mA2f 2
D 4π2mA2f 2
2
2 A spring-mass system experiences critical damping. Which graph represents the variation of the
displacement s with time t of the motion of the mass?
3 The oscillations of the particles between consecutive nodes of a standing wave have the same
A amplitude
B phase
C maximum velocity
D energy
4 Which statement is not true of an electromagnetic wave?
A It is a transverse wave.
B The expression for its speed is μ 0ε 0 .
C It consists of vibrations in magnetic and electric fields.
D It can be polarised.
960/3
68

73. Bahagian A [15 markah]
Jawab semua soalan dalam bahagian ini.
1 Satu zarah berjisim m melakukan gerakan harmonik ringkas dengan amplitud A dan frekuensi f.
Jumlah tenaga gerakan harmonik ringkas ini ialah
1
A mA2f 2
B 2mA2f 2
C 2π2mA2f 2
D 4π2mA2f 2
2
2 Satu sistem jisim-spring mengalami pelembapan genting. Graf yang manakah yang mewakili
ubahan sesaran s dengan masa t bagi gerakan jisim itu?
3 Ayunan satu zarah antara nod berturutan satu gelombang pegun mempunyai sama
A amplitud
B fasa
C halaju maksimum
D tenaga
4 Penyataan yang manakah yang tidak benar tentang gelombang elektromagnet?
A Merupakan gelombang melintang.
B Ungkapan bagi laju ialah μ 0ε 0 .
C Terdiri daripada getaran dalam medan magnet dan medan elektrik.
D Boleh dikutubkan.
960/3
69

74. 5 If the level of intensity of a sound is raised by 10 dB, what is the ratio of the new sound intensity
to the original sound intensity?
A 0.1 B 1 C 10 D 1010
6 A guitar wire is 0.80 m long and of mass 5.0 g. If its frequency of fundamental mode of vibration
is 100 Hz, its tension is
A 40 N B 128 N C 160 N D 200 N
7 Two thin lenses L1 and L2 which are placed coaxially at a distance 30 cm apart is shown in the
diagram below.
L1 L2
Each lens has a focal length of 40 cm. If the incident rays to L1 are parallel, the final image which
is produced after the rays pass through lenses L1 and L2 is
A real and located between L1 and L2
B virtual and located between L1 and L2
C real and located on the right side of L2
D virtual and located on the left side of L1
8 A concave mirror produces a virtual image at a distance 60 cm from the mirror. The height of the
image is three times the height of the object. What is the focal length of the concave mirror?
A 10 cm B 20 cm C 30 cm D 40 cm
9 The resolving power of an aperture can be increased by using
A an aperture of smaller diameter
B light with higher frequency
C light with longer wavelength
D light with higher intensity
960/3
70

75. 5 Jika paras keamatan satu bunyi dinaikkan sebanyak 10 dB, berapakah nisbah keamatan bunyi
baharu itu kepada keamatan bunyi asal?
A 0.1 B 1 C 10 D 1010
6 Seutas dawai gitar panjangnya 0.80 m dan berjisim 5.0 g. Jika frekuensi getaran mod asasnya
ialah 100 Hz, tegangannya ialah
A 40 N B 128 N C 160 N D 200 N
7 Dua kanta nipis L1 and L2 yang diletakkan sepaksi pada jarak 30 cm di antara satu sama lain
ditunjukkan dalam gambar rajah di bawah.
L1 L2
Setiap kanta mempunyai jarak fokus 40 cm. Jika sinar tuju ke L1 adalah selari, imej akhir yang
terhasil selepas sinar melalui kanta L1 dan L2 adalah
A nyata dan terletak di antara L1 dengan L2
B maya dan terletak di antara L1 dengan L2
C nyata dan terletak di sebelah kanan L2
D maya dan terletak di sebelah kiri L1
8 Satu cermin cekung menghasilkan satu imej maya pada jarak 60 cm dari cermin. Tinggi imej ialah
tiga kali daripada tinggi objek itu. Berapakah panjang fokus cermin cekung itu?
A 10 cm B 20 cm C 30 cm D 40 cm
9 Kuasa pembezaan jelas satu bukaan boleh ditingkatkan dengan menggunakan
A bukaan garis pusat yang lebih kecil
B cahaya dengan frekuensi yang lebih tinggi
C cahaya dengan panjang gelombang yang lebih panjang
D cahaya dengan keamatan yang lebih tinggi
960/3
71

76. 10 Which statement is not true of multimode step index optical fibres?
A The refractive index of the cladding layer is greater than that of the core index.
B The refractive index of the cladding layer is smaller than that of the core index.
C Total internal reflections occur at core-cladding boundaries.
D All wavelengths arrive at the other end of the fibre at different times.
11 When light with wavelength 300 nm incidents on the surface of a metal, photoelectrons with
maximum kinetic energy 2.0 eV are emitted from the surface of the metal. What is the maximum
wavelength for the light which can cause this emission of photoelectrons from the surface of the
metal?
A 200 nm B 600 nm C 650 nm D 880 nm
12 The characteristic lines in an X-ray spectrum is caused by
A deceleration of the energetic incident electrons while they approach the target
B collision of energetic incident electrons with the target atoms
C release of energy when the target atoms undergo ionisation
D transitions of electrons between innermost shells of the target atom
13 Nanoscience is generally known as the study on systems with
A sizes less than one nanometer
B sizes from one to one hundred nanometres
C mass of one to one hundred nanograms
D interaction time of one to one hundred nanoseconds
14 The binding energy per nucleon is
A almost constant when the nucleon number is between 60 and 80
B directly proportional to the nucleon number
C maximum when the nucleon number is between 1 to 20
D maximum when the nucleon number is between 220 to 240
15 The count rate of a radioactive sample was originally 208 s–1 as recorded by a detector. Four
minutes later, the count rate had decreased to 40 s–1. The average background count was found to be
16 s–1. What is the half-life of the radioactive sample?
A 30 s B 40 s C 60 s D 80 s
960/3
72

77. 10 Penyataan yang manakah yang tidak benar tentang gentian optik multimod indeks berperingkat?
A Indeks biasan lapisan salutan adalah lebih besar daripada indeks teras lapisan salutan.
B Indeks biasan lapisan salutan adalah lebih kecil daripada indeks teras lapisan salutan.
C Jumlah pesongan dalaman berlaku pada sempadan salutan teras.
D Semua panjang gelombang sampai di hujung yang lain gentian pada masa yang berbeza.
11 Apabila cahaya dengan panjang gelombang 300 nm tuju pada permukaan satu logam, fotoelektron
dengan tenaga kinetik maksimum 2.0 eV dipancarkan dari permukaan logam itu. Berapakah panjang
gelombang maksimum cahaya yang boleh menyebabkan pancaran fotoelektron ini dari permukaan
logam itu?
A 200 nm B 600 nm C 650 nm D 880 nm
12 Garis cirian dalam spektrum X-ray disebabkan oleh
A nyahpecutan elektron tuju yang bertenaga semasa menghampiri sasaran
B perlanggaran elektron tuju yang bertenaga dengan atom sasaran
C pembebasan tenaga apabila atom sasaran mengalami pengionan
D peralihan elektron di antara petala-petala yang paling dalam atom sasaran
13 Nanosains secara umumnya dikenali sebagai kajian terhadap sistem dengan
A saiz yang kurang daripada satu nanometer
B saiz daripada satu nanometer hingga seratus nanometer
C jisim satu nanogram hingga seratus nanogram
D interaksi masa satu nanosaat hingga seratus nanosaat
14 Tenaga pengikat per nukleon ialah
A hampir malar apabila nombor nukleon adalah di antara 60 dengan 80
B berkadar terus kepada nombor nukleon
C maksimum apabila nombor nukleon adalah di antara 1 hingga 20
D maksimum apabila nombor nukleon adalah di antara 220 hingga 240
15 Kadar bilang satu sampel radioaktif pada asalnya 208 s–1 seperti yang tercatat oleh satu pengesan.
Empat minit kemudian, kadar bilang telah berkurang kepada 40 s–1. Purata kadar bilang latar belakang
didapati menjadi 16 s–1. Berapakah setengah hayat sampel radioaktif itu?
A 30 s B 40 s C 60 s D 80 s
960/3
73

78. Section B [15 marks]
Answer all questions in this section.
16 A body of mass 2.0 kg moves in simple harmonic motion. The displacement x from the
equilibrium position at time t is given by x = 6.0cos 0.22π t , where x is in metres and t in seconds.
(a) Determine is the amplitude and the period of the simple harmonic motion. [3 marks]
(b) Calculate the maximum acceleration of the motion. [2 marks]
(c) Calculate the kinetic energy of the body at time t = 3 seconds. [3 marks]
17 In an electron diffraction experiment, an electron beam which is accelerated on a potential
difference is incident normally on a very thin gold film. Several circular diffraction rings are seen on a
photographic film.
(a) If the voltage at the anode is increased, what happens to the circular rings? [1 mark]
....................................................................................................................................................................
(b) If a particular ring of radius R is chosen and different values of accelerating voltage V are
1
recorded, sketch a graph of R against . Deduce that the experiment is in agreement with de
V
Broglie’s hypothesis. [6 marks]
960/3
74

79. Bahagian B [15 markah]
Jawab semua soalan dalam bahagian ini.
16 Satu jasad berjisim 2.0 kg bergerak dalam gerakan harmonik ringkas. Sesaran x daripada
kedudukan keseimbangan pada masa t berikan oleh x = 6.0cos 0.22π t , dengan x dalam meter dan t
dalam saat.
(a) Tentukan amplitud dan tempoh gerakan harmonik ringkas itu? [3 markah]
(b) Hitung pecutan maksimum gerakan itu. [2 markah]
(c) Hitung tenaga kinetik jasad itu pada masa t = 3 saat. [3 markah]
17 Dalam satu uji kaji belauan elektron, satu alur elektron yang dipecutkan pada satu beza keupayaan
menuju secara normal pada satu filem emas yang sangat nipis. Beberapa gelang belauan bulat dilihat
pada satu filem fotograf.
(a) Jika voltan pada anod ditingkatkan, apakah yang terjadi pada gelang bulat itu? [1 markah]
....................................................................................................................................................................
(b) Jika satu gelang tertentu yang berjejari R dipilih dan nilai berbeza voltan pecutan V
1
direkodkan, lakar graf R lawan . Deduksikan bahawa uji kaji itu bersetuju dengan hipotesis de
V
Broglie. [6 markah]
960/3
75

80. Section C [30 marks]
Answer any two questions in this section.
18 (a) The displacement y at distance x and time t of a sound wave propagating in air can be
represented by
y = 7.5 × 10−4 sin (315t − 1.05x),
where x and y are in metres and t in seconds.
T
(i) Sketch, on the same axes, graphs of y against x at times t = 0 and t = , where T is the
4
period of the wave. [2 marks]
(ii) Determine the velocity and the frequency of the wave. [4 marks]
(iii) Calculate the phase difference between the origin and a point 2.0 m from it. [3 marks]
(b) (i) What is meant by Doppler effect? [2 marks]
(ii) Describe the principle of Doppler radar used by the police to determine the speed of an
automobile. [4 marks]
960/3
76

81. Bahagian C [30 markah]
Jawab mana-mana dua soalan dalam bahagian ini.
18 (a) Sesaran y pada jarak x dan masa t suatu gelombang bunyi yang merambat di udara boleh
diwakili oleh
y = 7.5 × 10−4 sin (315t − 1.05x),
dengan x dan y dalam meter dan t dalam saat.
T
(i) Lakar, pada paksi yang sama, graf y lawan x pada masa t = 0 dan t = , dengan T kala
4
gelombang itu. [2 markah]
(ii) Tentukan halaju dan frekuensi gelombang itu. [4 markah]
(iii) Hitung beza fasa di antara asalan dengan satu titik 2.0 m dari asalan. [3 markah]
(b) (i) Apakah yang dimaksudkan dengan kesan Doppler? [2 markah]
(ii) Perihalkan prinsip radar Doppler yang digunakan oleh polis untuk menentukan laju
sesebuah kenderaan. [4 markah]
960/3
77

82. 19 (a) (i) State the principle of superposition. [2 marks]
(ii) Explain the conditions needed to obtain a well-defined interference pattern. [4 marks]
(b) The set-up for a Young’s double slit experiment is shown in the diagram below.
Light a
source
Red
filter
D
Screen
The fringe pattern observed has fringe separation of 1.6 mm.
D
(i) If is 2500, calculate the wavelength of the red light that passes through the filter.
a
[2 marks]
(ii) A blue filter is inserted to replace the red filter. Suggest what can be done to the set-up
to obtain the fringe pattern of the same fringe separation as in (b)(i). [2 marks]
(iii) If a thin sheet of mica with refractive index 1.58 is placed in front of the upper slit,
explain the changes occurred to the fringe pattern. [2 marks]
(iv) Given that the thickness of mica in (b)(iii) is 6.64 µm, calculate the shift of fringe
D
pattern using = 2500 and λ = 450 nm. [3 marks]
a
960/3
78

83. 19 (a) (i) Nyatakan prinsip superposisi. [2 markah]
(ii) Jelaskan syarat yang diperlukan untuk memperoleh satu corak interferen yang jelas.
[4 markah]
(b) Susunan bagi satu uji kaji dua celah Young ditunjukkan dalam gambar rajah di bawah.
Sumber a
cahaya
Penapis
merah D
Tabir
Corak pinggir yang dicerap mempunyai pemisahan pinggir 1.6 mm.
D
(i) Jika ialah 2500, hitung panjang gelombang cahaya merah yang melepasi melalui
a
penapis itu. [2 markah]
(ii) Satu penapis biru dimasukkan untuk menggantikan penapis merah itu. Cadangkan
apakah yang boleh dibuat kepada susunan untuk memperoleh corak pinggir dengan pemisahan pinggir
sama seperti dalam (b)(i). [2 markah]
(iii) Jika satu keping mika yang nipis dengan indeks biasan 1.58 diletakkan di hadapan
celah atas, jelaskan perubahan yang berlaku pada corak pinggir itu. [2 markah]
(iv)Diberikan bahawa tebal mika dalam (b)(iii) ialah 6.64 µm, hitung anjakan corak
D
pinggir menggunakan = 2500 dan λ = 450 nm. [3 markah]
a
960/3
79

84. 20 (a) (i) Explain nuclear fusion reaction. [2 marks]
(ii) State the conditions for nuclear fusion. [2 marks]
(b) Solar energy is produced by fusion reactions in the Sun. One of the fusion processes is known
as proton-proton cycle which involves reactions as shown below.
Reaction 1: 1
1H + 1H →
1
2
1H + 1 β + Q1
0
Reaction 2: 2
1H + 1H →
1
3
2 He + Q2
3 3 4
Reaction 3: 2 He + 2 He → 2 He + 2 1 H + Q3
1
Q1, Q2 and Q3 are energies released.
(i) Determine Q1, in Joules, released in Reaction 1. [3 marks]
(ii) Determine the number of protons required to form a helium nucleus 4 He in the above
2
continuous reactions. [2 marks]
(iii) Determine the total energy, in Joules, released in forming a helium nucleus 4 He .
2
[2 marks]
(iv) The Sun radiates 4.0 × 1026 W at a constant rate and the total mass of protons in the Sun
is 2.0 × 1030 kg. Determine the approximate life span of the Sun if it radiates energy by the proton-
proton cycle reaction. [4 marks]
[Atomic mass of 1 H is 1.00728 u, atomic mass of
1
2
1H is 2.01355 u, atomic mass of 1 β is
0
0.00055 u and atomic mass of 4 He is 4.00150 u.]
2
960/3
80

85. 20 (a) (i) Jelaskan tindak balas pelakuran nuklear. [2 markah]
(ii) Nyatakan syarat bagi pelakuran nuklear. [2 markah]
(b) Tenaga suria dihasilkan oleh tindak balas pelakuran dalam Matahari. Satu daripada proses
pelakuran dikenal sebagai kitar proton-proton yang melibatkan tindak balas seperti yang ditunjukkan
di bawah.
Tindak balas 1: 1
1H + 1H →
1
2
1H + 1 β + Q1
0
2
Tindak balas 2: 1H + 1H →
1
3
2 He + Q2
3 3 4
Tindak balas 3: 2 He + 2 He → 2 He + 2 1 H + Q3
1
Q1, Q2, dan Q3 ialah tenaga yang dibebaskan.
(i) Tentukan Q1, dalam Joule, yang dibebaskan oleh Tindak balas 1. [3 markah]
(ii) Tentukan nombor proton yang diperlukan untuk pembentukan satu nukleus helium
4
2 He dalam tindak balas selanjar di atas. [2 markah]
(iii) Tentukan jumlah tenaga, dalam Joule, yang dibebaskan dalam pembentukan satu
nukleus helium 4 He .
2 [2 markah]
(iv) Matahari memancarkan 4.0 × 1026 W pada kadar malar dan jumlah jisim proton dalam
Matahari ialah 2.0 × 1030 kg. Tentukan anggaran tempoh hayat Matahari jika Matahari memancarkan
tenaga melalui tindak balas kitar proton-proton. [4 markah]
[Jisim atom 1 H ialah 1.00728 u, jisim atom 2 H ialah 2.01355 u, jisim atom 1 β ialah 0.00055 u
1 1
0
dan jisim atom 4 He ialah 4.00150 u.]
2
960/3
81

86. Values of constants
(Nilai Pemalar)
Acceleration of free fall (Pecutan jatuh bebas) g = 9.81 m s−2
Avogadro constant (Pemalar Avogadro) NA = 6.02 × 1023 mol−1
Boltzmann constant (Pemalar Boltzmann) k, kB = 1.38 × 10−23 J K−1
Gravitational constant (Pemalar graviti) G = 6.67 × 10−11 N m2 kg−2
Magnitude of electronic (Magnitud cas elektron) e = 1.60 × 10−19 C
charge
Mass of the Earth (Jisim Bumi) ME = 5.97 × 1024 kg
Mass of the Sun (Jisim Matahari) MS = 1.99 × 1030 kg
Molar gas constant (Pemalar gas molar) R = 8.31 J K−1 mol−1
Permeability of free space (Ketelapan ruang bebas) μ0 = 4π × 10−7 H m−1
Permittivity of free space (Ketelusan ruang bebas) ε0 = 8.85 × 10−12 F m−1
= ⎛ 1 ⎞ −9 −1
⎜ ⎟ × 10 F m
⎝ 36π ⎠
Planck’s constant (Pemalar Planck) h = 6.63 × 10−34 J s
Radius of the Earth (Jejari Bumi) RE = 6.38 × 106 m
Radius of the Sun (Jejari Matahari) RS = 6.96 × 108 m
Rest mass of electron (Jisim rehat elektron) me = 9.11 × 10−31 kg
Rest mass of proton (Jisim rehat proton) mp = 1.67 × 10−27 kg
Speed of light in free space (Laju cahaya dalam ruang bebas) c = 3.00 × 108 m s−1
Stefan-Boltzmann constant (Pemalar Stefan-Boltzmann) σ = 5.67 × 10−8 W m−2 K−4
Unified atomic mass unit (Unit jisim atom bersatu) u = 1.66 × 10−27 kg
960/3
82

87. SPECIMEN EXPERIMENT
960/4 STPM
PHYSICS (FIZIK)
PAPER 4 (KERTAS 4)
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE)
© Majlis Peperiksaan Malaysia
STPM 960/4
83

88. STPM PHYSICS STUDENT’S MANUAL 20___/20___
Experiment
Topic: Direct current circuit
Title: Potentiometer
Objective: To determine the internal resistance of a cell using a potentiometer
Theory:
Accumulator
S1
l
Dry cell
S1
E.m.f. of the cell = ε.
Internal resistance of the cell = r.
With switch S1 closed while switch S2 open, obtain the balance length lo. With both S1 and S2
closed, obtain the balance length l.
Then,
ε = V + Ir
ε −V
r=
I
ε −V
r=
V
R
⎛ε ⎞
r = ⎜ − 1⎟ R
⎝ V ⎠
⎛l ⎞
r = ⎜ o − 1⎟ R
⎝l ⎠
lo ⎛1⎞
= r ⎜ ⎟ +1
l ⎝R⎠
⎛l ⎞ 1
Graph of ⎜ o ⎟ against should be linear and the gradient is r.
⎝l ⎠ R
960/4
84

89. STPM PHYSICS STUDENT’S MANUAL 20___/20___
Apparatus:
(i) A potentiometer
(ii) A resistor-pack
(iii) Two on-off switches
(iv) A jockey
(v) A 2 V accumulator
(vi) A 1.5 V dry cell
(vii) A centre-zero galvanometer
Procedure:
(a) With S1 closed and S2 open, determine the balance length lo.
(b) With both S1 and S2 closed, determine the balance length l for various values of R.
lo 1
(c) Plot a graph of against .
l R
(d) Calculate the internal resistance r of the cell.
960/4
85

90. 86

91. Identity card number:………………………….. Centre number/index number:……………………….
(Nombor kad pengenalan) (Nombor pusat/angka giliran)
SPECIMEN PAPER
960/5 STPM
PHYSICS (FIZIK)
PAPER 5 (KERTAS 5)
One and a half hours (Satu jam setengah)
MAJLIS PEPERIKSAAN MALAYSIA
(MALAYSIAN EXAMINATIONS COUNCIL)
SIJIL TINGGI PERSEKOLAHAN MALAYSIA
(MALAYSIA HIGHER SCHOOL CERTIFICATE)
Instructions to candidates:
DO NOT OPEN THIS QUESTION PAPER UNTIL YOU ARE TOLD TO DO SO.
Answer all questions. Write your answer in the spaces provided. All working should be shown.
Numerical answers should be given to an appropriate number of significant figures; units should
be quoted where appropriate.
Arahan kepada calon:
JANGAN BUKA KERTAS SOALAN INI SEHINGGA ANDA DIBENARKAN BERBUAT
DEMIKIAN.
Jawab semua soalan. Tulis jawapan anda dalam ruang yang disediakan. Semua kerja
hendaklah ditunjukkan.
Jawapan berangka hendaklah diberikan hingga bilangan angka bererti yang sesuai; unit
hendaklah dinyatakan di mana-mana yang sesuai.
This question paper consists of printed pages and blank page.
(Kertas soalan ini terdiri daripada halaman bercetak dan halaman kosong.)
© Majlis Peperiksaan Malaysia
STPM 960/5
87

92. dQ
1 The rate of heat loss of a hot body at temperature θ to the surroundings at temperature θ 0 is
dt
given by
dQ
= kA(θ − θ 0 ),
dt
where k is a constant which depends on the nature of its surface and A the surface area of the body
which is exposed to the surroundings. The rate at which thermal energy is lost from the body is given
by
dQ dθ
= − mc ,
dt dt
where m is the mass of the body and c the specific heat capacity of the body. Thus
dθ kA
=− (θ − θ 0 ) .
dt mc
An apparatus set-up used by a student to study the rate of cooling of a body is shown in the
diagram below.
Starting with water which was nearly boiling, the student recorded the temperature θ of hot water
at time t for each five minute interval, with the temperature of the surroundings θ 0 = 27 °C. Then the
student plotted a graph of θ against t as shown in page __.
960/5
88

93. dQ
1 Kadar kehilangan haba satu jasad panas pada suhu θ kepada persekitaran pada suhu θ 0
dt
diberikan oleh
dQ
= kA(θ − θ 0 ),
dt
dengan k pemalar yang bergantung pada sifat permukaannya dan A luas permukaan jasad yang
terdedah kepada persekitaran. Kadar kehilangan tenaga terma daripada jasad itu diberikan oleh
dQ dθ
= − mc ,
dt dt
dengan m jisim jasad dan c muatan haba tentu jasad itu. Oleh itu
dθ kA
=− (θ − θ 0 ) .
dt mc
Susunan radas yang digunakan oleh seorang pelajar untuk mengkaji kadar penyejukan satu jasad
ditunjukkan dalam gambar rajah di bawah.
Termometer
Pengacau
Penutup kayu
Bikar
Air panas
Pelapik kayu
Bermula dengan air yang hampir mendidih, pelajar itu mencatat suhu θ air panas pada masa t bagi
setiap selang lima minit, dengan suhu persekitaran θ 0 = 27 °C. Pelajar itu kemudian memplot graf θ
lawan t seperti yang ditunjukkan pada halaman __.
960/5
89

94. 960/5
90

95. Graf θ lawan t
960/5
91

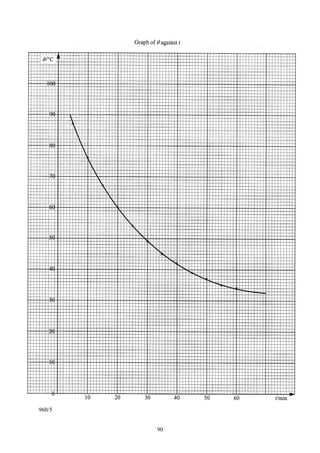
96. (a) On the graph of θ against t, draw tangent lines at θ = 40 °C, 50 °C, 60 °C, 70 °C and 80 °C,
dθ dθ
and determine the corresponding slopes . Tabulate θ, (θ − θ 0 ) and . [5 marks]
dt dt
960/5
92

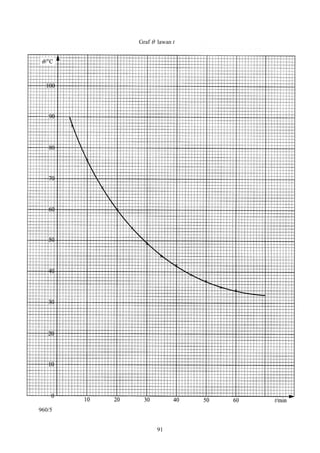
97. (a) Pada graf θ lawan t, lukis garis tangen pada θ = 40 °C, 50 °C, 60 °C, 70 °C, dan 80 °C, dan
dθ dθ
tentukan kelerengan yang sepadan. Jadualkan θ, (θ − θ0), dan . [5 markah]
dt dt
960/5
93

98. dθ
(b) Plot a graph of against (θ − θ 0 ) . [5 marks]
dt
960/5
94

99. dθ [5 markah]
(b) Plot graf lawan (θ − θ 0 ).
dt
960/5
95

100. (c) State two precautionary measures which need to be taken so that the variation of temperature
θ of hot water with time t in the cooling process gives a good result. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
dθ
(d) Given that m = 1.0 kg, c = 4200 J kg−1 K−1 and A = 0.1 m2. Based on the graph of
dt
against (θ − θ 0 ) , determine the value of k for the apparatus set-up. [3 marks]
960/5
96

101. (c) Nyatakan dua langkah berjaga-jaga yang perlu diambil supaya ubahan suhu θ air panas
dengan masa t dalam proses penyejukan itu memberikan keputusan yang baik. [2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
dθ
(d) Diberikan m = 1.0 kg, c = 4200 J kg−1 K−1, dan A = 0.1 m2. Berdasarkan graf
dt
lawan (θ − θ 0 ) , tentukan nilai k bagi susunan radas itu. [3 markah]
960/5
97

102. 2 An apparatus set-up to determine the resistivity of a wire is shown in the diagram below.
J
O P
Initially the wire of length is placed between O and P. The switch was closed and an ammeter
reading I was recorded. The jockey was then touched and slid along the wire until the original
reading I was obtained at point J. The distance x was then measured and recorded. The experiment
was repeated using different values of .
The readings of , I and x obtained are as follows.
( ± 0.1) cm 105 100 95 90 85
(I ± 0.01) A 0.72 0.74 0.80 0.82 0.84
(x ± 0.1) cm 64.0 63.3 55.7 52.7 51.5
The diameters D of the wire for three different measurements were recorded as 0.56 mm,
0.57 mm and 0.56 mm.
πD 2 E
The resistivity ρ of the wire is given by ρ = , where E is the e.m.f. of the dry cell.
4 Ix
(a) If E = 1.5 V, calculate the value of ρ and its error without using the graphical method.
[4 marks]
(b) Describe a simple method to determine the e.m.f. of the dry cell. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
960/5
98

103. 2 Susunan radas untuk menentukan kerintangan seutas dawai ditunjukkan dalam gambar rajah
di bawah.
Akumulator Suis
J Dawai gelongsor
O P
Joki
Sel kering
Pada mulanya seutas dawai yang panjangnya ditempatkan di antara O dengan P. Suis ditutup
dan bacaan ammeter I direkodkan. Joki kemudian disentuhkan dan digelongsorkan pada dawai
tersebut sehingga bacaan I yang asal diperoleh di titik J. Jarak x kemudian diukur dan direkodkan. Uji
kaji ini diulangi dengan menggunakan nilai yang berlainan.
Bacaan , I, dan x yang diperoleh adalah seperti yang berikut.
( ± 0.1) cm 105 100 95 90 85
(I ± 0.01) A 0.72 0.74 0.80 0.82 0.84
(x ± 0.1) cm 64.0 63.3 55.7 52.7 51.5
Garis pusat D dawai untuk tiga pengukuran yang berlainan direkodkan sebagai 0.56 mm,
0.57 mm, dan 0.56 mm.
πD 2 E
Kerintangan ρ dawai tersebut diberikan sebagai ρ = , dengan E sebagai d.g.e. sel kering.
4 Ix
(a) Jika E = 1.5 V, hitung nilai ρ dan ralatnya tanpa menggunakan kaedah bergraf. [4 markah]
(b) Perihalkan satu kaedah ringkas untuk menentukan d.g.e. sel kering itu. [2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
960/5
99

104. (c) The position of J determined in this experiment is called the balance point. With the aid of a
diagram, describe another way to determine the position of J using the same apparatus and a
galvanometer. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
(d) In this experiment, it was found that the accuracy of the experiment would increase when a
longer slide wire was used. Explain why this is the case. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
(e) Suggest two precautions which should be taken in order to increase the accuracy of the
experiment. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
960/5
100

105. (c) Kedudukan J yang ditentukan dalam uji kaji ini disebut titik keseimbangan. Dengan bantuan
gambar rajah, perihalkan satu cara lain untuk menentukan kedudukan J dengan menggunakan radas
yang sama dan sebuah galvanometer. [2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
(d) Dalam uji kaji ini, didapati bahawa kejituan uji kaji akan meningkat apabila dawai gelongsor
yang lebih panjang digunakan. Jelaskan mengapa hal ini demikian. [2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
(e) Cadangkan dua langkah berjaga-jaga yang perlu diambil untuk meningkatkan kejituan uji kaji
ini. [2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
960/5
101

106. (f) Using the data and resistivity formula given, describe briefly the graphical method to
determine the resistivity ρ of wire. [3 marks]
960/5
102

107. (f) Dengan menggunakan data dan rumus kerintangan yang diberikan, perihalkan secara ringkas
kaedah bergraf untuk menentukan kerintangan ρ dawai. [3 markah]
103

108. 3 (a) State a simple method to estimate the focal length of a convex lens. [1 mark]
....................................................................................................................................................................
....................................................................................................................................................................
(b) An apparatus set-up to determine the focal length of a convex lens is shown in the diagram
below. A light bulb was used as an object.
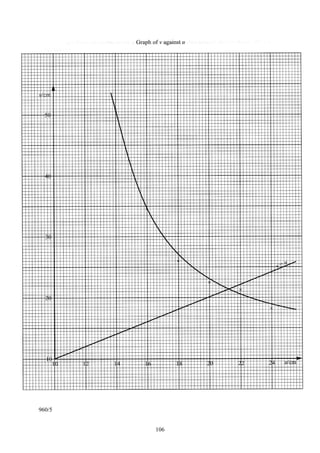
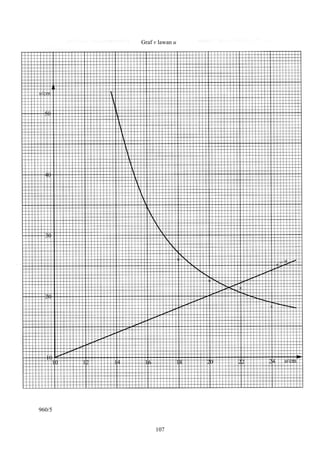
A student obtained several object distances u and the corresponding image distances v. A graph
of v against u was then plotted as shown on page . A graph of v = u was also drawn.
Determine the focal length f1 of the convex lens from the graphs. [3 marks]
960/5
104

109. 3 (a) Nyatakan kaedah ringkas untuk menganggar panjang fokus satu kanta cembung. [1 markah]
....................................................................................................................................................................
....................................................................................................................................................................
(b) Susunan radas untuk menentukan panjang fokus satu kanta cembung ditunjukkan seperti
dalam gambar rajah di bawah. Satu mentol digunakan sebagai objek.
Kanta
cembung Tabir
Mentol
Plastisin
Seorang pelajar memperoleh beberapa jarak objek u dan jarak imej v yang sepadan. Satu graf v
lawan u kemudian diplot seperti yang ditunjukkan pada halaman . Graf v = u juga dilukis.
Tentukan panjang fokus f1 kanta cembung dari graf itu. [3 markah]
960/5
105

110. raph of v against u
960/5
106

111. Graf v lawan u
960/5
107

112. (c) A concave lens was then placed in contact with the convex lens to form a combined lens as
shown in the diagram below. The experiment was repeated.
(i) The results were recorded. Complete the table. [2 marks]
1 1
u/cm v/cm /cm−1 /cm−1
u v
100.00 25.5
67.0 30.0
50.0 35.9
40.0 38.5
33.0 57.0
25.0 154.0
960/5
108

113. (c) Satu kanta cekung kemudian diletakkan bersentuhan dengan kanta cembung itu untuk
membentuk satu kanta gabungan seperti yang ditunjukkan dalam gambar rajah di bawah. Uji kaji
diulangi.
Kanta
cembung Kanta Tabir
cekung
Mentol
Plastisin
(i) Keputusan direkodkan. Lengkapkan jadual ini. [2 markah]
1 1
u/cm v/cm /cm−1 /cm−1
u v
100.00 25.5
67.0 30.0
50.0 35.9
40.0 38.5
33.0 57.0
25.0 154.0
960/5
109

114. 1 1
(ii) Plot a graph of against , and extrapolate the line to intersect both the axes.
v u
[3 marks]
960/5
110

115. 1 1
(ii) Plot graf lawan , dan ekstrapolasikan garis itu untuk memotong kedua-dua paksi.
v u
[3 markah]
960/5
111

116. (iii) Write down the value of the intercept on each axis, and determine the focal length f of
the combined lens. [2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
(iv) Based on your graph, state two reasons why the experiment is considered not accurate.
[2 marks]
....................................................................................................................................................................
....................................................................................................................................................................
(d) The focal length f of the combined lens is related to the focal length f1 of the convex lens and
the focal length f2 of the concave lens by the equation
1 1 1
= + .
f f1 f2
Calculate the focal length f2 of the concave lens. [2 marks]
960/5
112

117. (iii) Tulis nilai pintasan pada setiap paksi, dan tentukan panjang fokus f kanta gabungan.
[2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
(iv) Berdasarkan graf anda, nyatakan dua sebab mengapa uji kaji itu dianggap tidak jitu.
[2 markah]
....................................................................................................................................................................
....................................................................................................................................................................
(d) Panjang fokus f kanta gabungan dihubungkan dengan panjang fokus f1 kanta cembung dan
panjang fokus f2 kanta cekung oleh persamaan
1 1 1
= + .
f f1 f2
Hitung panjang fokus f2 kanta cekung itu. [2 markah]
960/5
113