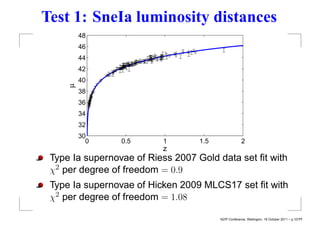
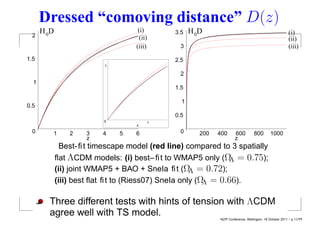
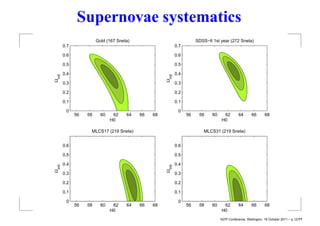
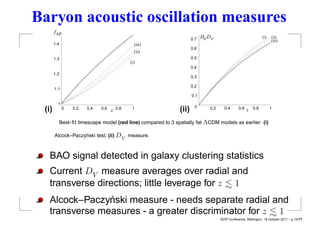
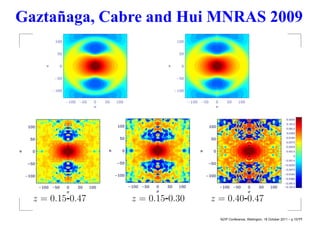
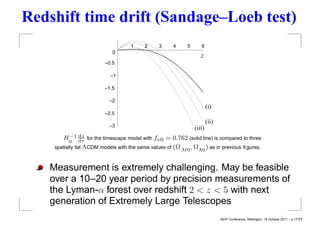
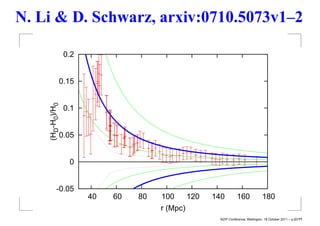
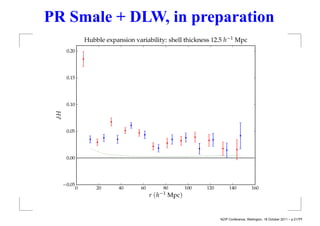
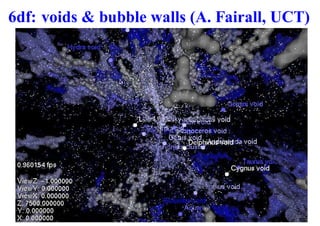
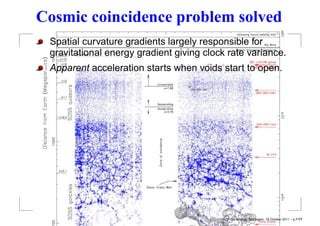
This document summarizes David Wiltshire's timescape cosmology, an alternative to the standard cosmological model that accounts for large scale inhomogeneities in the universe. It proposes that spatial curvature gradients between overdense walls and underdense voids can lead to differences in the calibration of clocks and rulers between local observers and globally averaged observers. Several observational tests are discussed that provide tentative support for the timescape scenario over LambdaCDM, including supernova luminosity distances, baryon acoustic oscillations, and predictions of Hubble flow variance.

1. Observational Tests of the
Timescape Cosmology
David L. Wiltshire (University of Canterbury, NZ)
DLW: New J. Phys. 9 (2007) 377
Phys. Rev. Lett. 99 (2007) 251101
Phys. Rev. D78 (2008) 084032
Phys. Rev. D80 (2009) 123512
Class. Quantum Grav. 28 (2011) 164006
B.M. Leith, S.C.C. Ng & DLW:
ApJ 672 (2008) L91
P.R. Smale & DLW, MNRAS 413 (2011) 367
P.R. Smale, MNRAS (2011) in press
NZIP Conference, Wellington, 18 October 2011 – p.1/??

2. Overview of timescape cosmology
Standard cosmology, with 22% non-baryonic dark
matter, 74% dark energy assumes universe expands as
smooth fluid, ignoring structures on scales
< 100h−1 Mpc
∼
Actual observed universe contains vast structures of
voids (most of volume), plus walls and filaments
containing galaxies
Timescape scenario - first principles model reanalysing
coarse-graining of “dust” in general relativity
Hypothesis: must understand nonlinear evolution with
backreaction, AND gravitational energy gradients within
the inhomogeneous geometry
NZIP Conference, Wellington, 18 October 2011 – p.2/??

3. 6df: voids & bubble walls (A. Fairall, UCT)
NZIP Conference, Wellington, 18 October 2011 – p.3/??

4. Within a statistically average cell
Need to consider relative position of observers over
scales of tens of Mpc over which δρ/ρ ∼ −1.
GR is a local theory: gradients in spatial curvature and
gravitational energy can lead to calibration differences
between our rulers and clocks and volume average
ones
NZIP Conference, Wellington, 18 October 2011 – p.4/??

5. −10
Relative deceleration scale
10 m/s 2
0.12
α
1.2 0.10
α /(Hc)
1.0 0.08
0.8 0.06
0.04
0.6
0.02 α /(Hc)
0.4
(i) 0 0.05 0.1 z 0.15 0.2 0.25
(ii) 0 2 4 z 6 8 10
Instantaneous relative volume deceleration of walls relative to volume average background
q
˙
α = H0 c¯ w γ w /(
γ ¯ γ 2 − 1) computed for timescape model which best fits supernovae
¯w
luminosity distances: (i) as absolute scale nearby; (ii) divided by Hubble parameter to large z .
With α0 ∼ 7 × 10−11 m s−2 and typically α ∼ 10−10 m s−2 for
most of life of Universe, get 37% difference in
calibration of volume average clocks relative to our own
NZIP Conference, Wellington, 18 October 2011 – p.5/??

6. Apparent cosmic acceleration
Volume average observer sees no apparent cosmic
acceleration
2 (1 − fv )2
q=
¯ 2
.
(2 + fv )
As t → ∞, fv → 1 and q → 0+ .
¯
A wall observer registers apparent cosmic acceleration
− (1 − fv ) (8fv 3 + 39fv 2 − 12fv − 8)
q= ,
2 2
4 + fv + 4fv
Effective deceleration parameter starts at q ∼ 1 , for
2
small fv ; changes sign when fv = 0.58670773 . . ., and
approaches q → 0− at late times.
NZIP Conference, Wellington, 18 October 2011 – p.6/??

7. Cosmic coincidence problem solved
Spatial curvature gradients largely responsible for
gravitational energy gradient giving clock rate variance.
Apparent acceleration starts when voids start to open.
NZIP Conference, Wellington, 18 October 2011 – p.7/??

8. Best fit parameters
Hubble constant H0 + ∆H0 = 61.7+1.2 km/s/Mpc
−1.1
+0.12
present void volume fraction fv0 = 0.76−0.09
¯
bare density parameter ΩM 0 = 0.125+0.060
−0.069
dressed density parameter ΩM 0 = 0.33+0.11
−0.16
non–baryonic dark matter / baryonic matter mass ratio
¯ ¯ ¯
(ΩM 0 − ΩB0 )/ΩB0 = 3.1+2.5
−2.4
¯
bare Hubble constant H 0 = 48.2+2.0 km/s/Mpc
−2.4
mean phenomenological lapse function γ 0 = 1.381+0.061
¯ −0.046
+0.0120
deceleration parameter q0 = −0.0428−0.0002
wall age universe τ0 = 14.7+0.7 Gyr
−0.5
NZIP Conference, Wellington, 18 October 2011 – p.8/??

9. Key observational tests
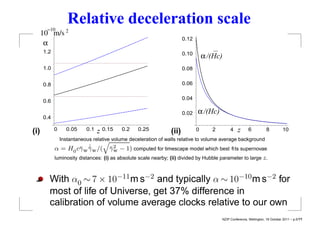
Best–fit parameters: H0 = 61.7+1.2 km/s/Mpc, Ωm = 0.33+0.11
−1.1 −0.16
(1σ errors for SneIa only) [Leith, Ng & Wiltshire, ApJ 672
(2008) L91]
NZIP Conference, Wellington, 18 October 2011 – p.9/??

10. Test 1: SneIa luminosity distances
48
46
44
42
40
µ
38
36
34
32
30
0 0.5 1 1.5 2
z
Type Ia supernovae of Riess 2007 Gold data set fit with
χ2 per degree of freedom = 0.9
Type Ia supernovae of Hicken 2009 MLCS17 set fit with
χ2 per degree of freedom = 1.08
NZIP Conference, Wellington, 18 October 2011 – p.10/??

11. Dressed “comoving distance” D(z)
H 0D (i) 3.5 H 0D (i)
2 (ii) (ii)
(iii) 3 (iii)
1.5 2.5
1
2
1
1.5
1
0.5
0.5
0 1
z
0 1 2 3 4 5 6 0 200 400 600 800 1000
z z
Best-fit timescape model (red line) compared to 3 spatially
flat ΛCDM models: (i) best–fit to WMAP5 only (Ω = 0.75);
Λ
(ii) joint WMAP5 + BAO + SneIa fit (Ω = 0.72);
Λ
(iii) best flat fit to (Riess07) SneIa only (Ω = 0.66).
Λ
Three different tests with hints of tension with ΛCDM
agree well with TS model.
NZIP Conference, Wellington, 18 October 2011 – p.11/??

12. Supernovae systematics
Gold (167 SneIa) SDSS−II 1st year (272 SneIa)
0.7 0.7
0.6 0.6
0.5 0.5
0.4 0.4
Ωm0
m0
Ω
0.3 0.3
0.2 0.2
0.1 0.1
0 0
56 58 60 62 64 66 68 56 58 60 62 64 66 68
H0 H0
MLCS17 (219 SneIa) MLCS31 (219 SneIa)
0.6 0.6
0.5 0.5
0.4 0.4
Ωm0
m0
Ω
0.3 0.3
0.2 0.2
0.1 0.1
0 0
56 58 60 62 64 66 68 56 58 60 62 64 66 68
H0 H0
NZIP Conference, Wellington, 18 October 2011 – p.12/??

13. Recent Sne Ia results; PR Smale + DLW
SALT/SALTII fits (Constitution,SALT2,Union2) favour
ΛCDM over TS: ln BTS:ΛCDM = −1.06, −1.55, −3.46
MLCS2k2 (fits MLCS17,MLCS31,SDSS-II) favour TS
over ΛCDM: ln BTS:ΛCDM = 1.37, 1.55, 0.53
Different MLCS fitters give different best-fit parameters;
e.g. with cut at statistical homogeneity scale, for
MLCS31 (Hicken et al 2009) ΩM 0 = 0.12+0.12 ;
−0.11
MLCS17 (Hicken et al 2009) ΩM 0 = 0.19+0.14 ;
−0.18
SDSS-II (Kessler et al 2009) ΩM 0 = 0.42+0.10
−0.10
Supernovae systematics (reddening/extinction, intrinsic
colour variations) must be understood
TS model most obviously consistent if dust in other
galaxies not significantly different from Milky Way
NZIP Conference, Wellington, 18 October 2011 – p.13/??

14. Baryon acoustic oscillation measures
f AP
0.7 H0 D V (i) (ii)
(iii)
1.4 (iii)
0.6
(ii)
1.3 0.5
(i)
0.4
1.2
0.3
0.2
1.1
0.1
1
0
(i) 0 0.2 0.4 0.6 z 0.8 1 (ii) 0.2 0.4 0.6 z 0.8 1
Best-fit timescape model (red line) compared to 3 spatially flat ΛCDM models as earlier: (i)
nski test; (ii) DV measure.
Alcock–Paczy´
BAO signal detected in galaxy clustering statistics
Current DV measure averages over radial and
<
transverse directions; little leverage for z ∼ 1
Alcock–Paczy´nski measure - needs separate radial and
<
transverse measures - a greater discriminator for z ∼ 1
NZIP Conference, Wellington, 18 October 2011 – p.14/??

15. Gaztañaga, Cabre and Hui MNRAS 2009
z = 0.15-0.47 z = 0.15-0.30 z = 0.40-0.47
NZIP Conference, Wellington, 18 October 2011 – p.15/??

16. Gaztañaga, Cabre and Hui MNRAS 2009
redshift Ω M 0 h2 ΩB0 h2 ΩC0 /ΩB0
range
0.15-0.30 0.132 0.028 3.7
0.15-0.47 0.12 0.026 3.6
0.40-0.47 0.124 0.04 2.1
Tension with WMAP5 fit ΩB0 0.045, ΩC0 /ΩB0 6.1 for
LCDM model.
GCH bestfit: ΩB0 = 0.079 ± 0.025, ΩC0 /ΩB0 3.6.
TS prediction ΩB0 = 0.080+0.021 , ΩC0 /ΩB0 = 3.1+1.8 with
−0.013 −1.3
match to WMAP5 sound horizon within 4% and no 7 Li
anomaly.
NZIP Conference, Wellington, 18 October 2011 – p.16/??

17. Redshift time drift (Sandage–Loeb test)
1 2 3 4 5 6
0
z
–0.5
–1
–1.5
–2
(i)
–2.5
(ii)
–3 (iii)
−1 dz
H0 dτ for the timescape model with fv0 = 0.762 (solid line) is compared to three
spatially flat ΛCDM models with the same values of (Ω M 0 , ΩΛ0 ) as in previous figures.
Measurement is extremely challenging. May be feasible
over a 10–20 year period by precision measurements of
the Lyman-α forest over redshift 2 < z < 5 with next
generation of Extremely Large Telescopes
NZIP Conference, Wellington, 18 October 2011 – p.17/??

18. Apparent Hubble flow variance
NZIP Conference, Wellington, 18 October 2011 – p.18/??

19. Apparent Hubble flow variance
As voids occupy largest volume of space expect to
measure higher average Hubble constant locally until
the global average relative volumes of walls and voids
are sampled at scale of homogeneity; thus expect
maximum H0 value for isotropic average on scale of
dominant void diameter, 30h−1 Mpc, then decreasing til
levelling out by 100h−1 Mpc.
Consistent with a Hubble bubble feature (Jha, Riess,
Kirshner ApJ 659, 122 (2007)); or “large scale flows”
with certain characteristics (cf Watkins et al).
Expected maximum “bulk dipole velocity”
¯ 30
vpec = ( 3H0
2 − H0 ) Mpc = 510+210 km/s
h −260
NZIP Conference, Wellington, 18 October 2011 – p.19/??

20. N. Li & D. Schwarz, arxiv:0710.5073v1–2
0.2
0.15
(HD-H0)/H0
0.1
0.05
0
-0.05
40 60 80 100 120 140 160 180
r (Mpc)
NZIP Conference, Wellington, 18 October 2011 – p.20/??

21. PR Smale + DLW, in preparation
NZIP Conference, Wellington, 18 October 2011 – p.21/??

22. The value of H0
Value of H0 = 74.2 ± 3.6 km/s/Mpc of SH0 ES survey (Riess
et al., 2009) calibrated by NGC4258 maser distance at 7.5
Mpc is a challenge for the timescape model. BUT
Expect variance in Hubble flow below scale of
homogeneity with typical higher value
Hvw0 = 72.3 km/s/Mpc at 30h−1 Mpc scale
H0 determinations independent of local distance ladder:
WiggleZ FLRW BAO value (Beutler et al,
arXiv:1106.3366): H0 = 67 ± 3.2 km/s/Mpc
Quasar strong lensing time delays; e.g., (Courbin et al,
1009.1473): H0 = 62+6 km/s/Mpc
−4
Megamaser distance of UGC3789 H0 = 66.6 ± 11.4
km/s/Mpc, (69 ± 11 km/s/Mpc with“flow modeling”).
NZIP Conference, Wellington, 18 October 2011 – p.22/??

23. Summary
Apparent cosmic acceleration can be understood purely
within general relativity; by (i) treating geometry of
universe more realistically; (ii) understanding
fundamental aspects of general relativity of statistical
description of general relativity which have not been
fully explored – quasi–local gravitational energy,
of gradients in spatial curvature etc.
Extra ingredients – regional averages etc – go beyond
conventional applications of general relativity
Description of spacetime as a causal relational
structure – retains principles consistent with GR
Many details – averaging scheme etc – may change,
but fundamental questions remain in any approach
NZIP Conference, Wellington, 18 October 2011 – p.23/??

24. Outlook
Other work
Several observational tests (Alcock-Paczynski test,
Clarkson, Bassett and Lu test, redshift time drift etc)
discussed in PRD 80 (2009) 123512
Work in progress
´
Adapting Korzynski’s “covariant coarse-graining”
approach to more rigorously define regional averages
(with James Duley)
Analysis of variance of Hubble flow in style of Li and
Schwarz on large datasets (with Peter Smale)
Full analysis of CMB anisotropy spectrum in timescape
model (with Ahsan Nazer)
NZIP Conference, Wellington, 18 October 2011 – p.24/??