Tài liệu cung cấp các phương pháp giải và phân tích các phương trình và bất phương trình toán học, bao gồm việc khảo sát hàm số và các giải pháp cho các bài toán cụ thể. Các bài tập minh họa chi tiết quy trình giải quyết với các ví dụ liên quan đến hàm số và phương trình khác nhau. Nó cũng thảo luận về sự ảnh hưởng của các tham số đến nghiệm của phương trình.

1. Bi n lu n phương trình, b t phương trình b ng th
99
BI N LU N PHƯƠNG TRÌNH, BPT B NG TH
I. BI N LU N PHƯƠNG TRÌNH B NG TH
1. Bài toán: a) Kh o sát và v th (C): y = f (x)
b) Bi n lu n theo m s nghi m: F(x, m) = 0
2. Phương pháp: b) Bi n i F(x, m) = 0 v 1 trong 4 d ng sau:
D ng 1: ƒ(x) = m D ng 2: ƒ(x) = g(m)
D ng 3: ƒ(x) = ax + g(m) D ng 4: ƒ(x) = g(m) (x − x0) + y0
3. Các bài t p m u minh h a
Bài 1. 1) Kh o sát s bi n thiên và v th ( )
2
3 3( ):
2
x xC y f x
x
+ += =
+
2) Bi n lu n theo a s nghi m c a PT: ( )2
3 3 2 0x a x a+ − + − = và so sánh các
nghi m ó v i (−3) và (−1)
Gi i: 1) 1.1. T p xác nh: { } ( ) ( )D 2 , 2 2,f = − = −∞ − − +∞» ∪
1.2. Chi u bi n thiên:
a) o hàm và c c tr :
( )
2 1
2
2
3
4 3 0
2 1
x x
x xy
x x x
= = −
+ +′ = = ⇔ 
+ = = −
⇒ ( ) ( ) ( ) ( )1 23 3; 1 1f x f f x f= − = − = − =
b) Ti m c n: ( ) 11
2
f x x
x
= + +
+
( )
2
2 1
3 3
lim lim
2x x
x x
f x
x→ − →−
+ +
= = ∞
+
⇒ TC : x = −2.
( ) ( ) 1lim 1 lim 0
2x x
f x x
x→∞ →∞
 − + = =  +
⇒ TCX: y = x + 1.
c) B ng bi n thiên:
x −∞ −3 −2 −1 +∞
( )f x′ + 0 − − 0 +
( )f x
−∞
−3
−∞
+∞
1
+∞
www.VNMATH.com

2. Chương I. Hàm s – Tr n Phương
100
d) Nh n xét: Hàm s ng bi n trên ( ) ( ), 3 1,−∞ − − +∞∪
Hàm s ngh ch bi n trên ( ) ( )3, 2 2, 1− − − −∪ ;
Hàm s có c c i ( )3, 3− − và c c ti u (−1, 1)
2) PT ( )2
3 3 2x x a x⇔ + + = +
( )
2
3 3
2
x xf x a
x
+ +⇔ = =
+
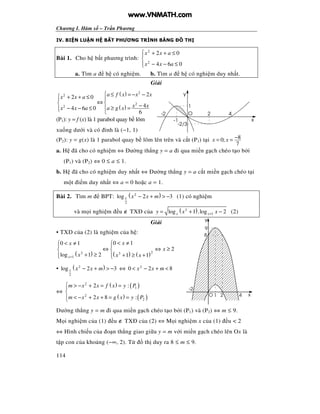
Nghi m c a phương trình ã cho là hoành
giao i m c a ư ng th ng y a= v i th
(C): y = f (x). Nhìn vào th ta có:
N u a < −3 thì x1 < −3 < x2 < −1 N u a = −3 thì x1 = x2 = −3 < −1
N u −3 < a < 1 thì phương trình vô nghi m.
N u a = 1 thì −3 < −1 = x1 = x2 N u a > 1 thì −3 < x1 < −1 < x2
Bài 2. a. Kh o sát và v th ( )
2
( ):
1
xC y f x
x
= =
−
b. Bi n lu n s nghi m c a PT: ( )4 3 2
2 1 0z mz m z mz− + + − + =
c. Bi n lu n s nghi m t∈(0,π) c a PT: 2
cos cos 0t m t m− + =
Gi i
( ) 11
1
f x x
x
= + +
−
⇒
TCÐ: 1
TCX: 1
x
y x
=

= +
( ) ( )
( )2
0 02
0
1 2 4
x yx x
f x
x x y
= ⇒ =−′ = = ⇔ 
− = ⇒ =
(T l p BBT)
b. ( )4 3 2
2 1 0z mz m z mz− + + − + =
⇔ ( )2
2
12 0mz mz m
z z
− + + − + =
⇔ ( ) ( )
2
1 1 0z m z m
z z
+ − + + = . t 1 1 2x z x z
z z
= + ⇒ = + ≥ ,
( )2
1x m x= − ⇔ ( )
2
1
xf x m
x
= =
−
v i ( ] [ )D , 2 2,x∈ = −∞ − +∞∪
c) t ( ) ( )cos 1,1 0,x t t= ∈ − ∀ ∈ π . Khi ó 2
cos cos 0t m t m− + =
⇔ ( )
2
1
xf x m
x
= =
−
v i x ∈ (−1, 1).
1 2-1
1
4
x
y
O
O x
y
1
-1
-3
-3 -2
y=a
x21x
a
1.3. th :
www.VNMATH.com

3. Bi n lu n phương trình, b t phương trình b ng th
101
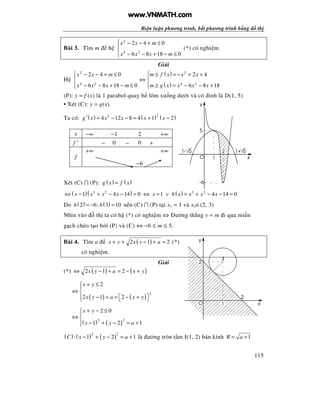
Bài 3. a. Kh o sát và v
2
3
2
x xy
x
+ −=
+
b. Bi n lu n theo m s nghi m: ( )4 2
1 3 2 0t m t m+ − − − =
Gi i
a.
TCÐ: 211
2 TCX : 1
x
y x
x y x
=
= − − ⇒ 
+ = −
( )2
11 0 2
2
y x
x
′ = + > ∀ ≠ −
+
b. ( )4 2
1 3 2 0t m t m+ − − − =
⇔ ( )4 2 2
3 2t t m t+ − = + ⇔
4 2
2
3
2
t t m
t
+ − =
+
⇔ ( )
2
3
2
x xf x m
x
+ −= =
+
v i x = t2
≥ 0
Bài 4. a) Kh o sát và v th ( )
2
1( ):
1
x xC y f x
x
+ += =
+
b) Bi n lu n s nghi m c a PT: ( )2
1 1 0x m x m+ − + − =
c) Bi n lu n s nghi m x∈[0,π] c a PT: ( )2
sin 1 sin 1 0x a x a− − + − =
Gi i
( ) 1
1
f x x
x
= +
+
⇒
TCÐ: 1
TCX : 1
x
y x
=

= +
( ) ( )
( )2
2 22
0
1 0 1
x yx x
f x
x x y
= − ⇒ = −+′ = = ⇔ 
+ = ⇒ =
x −∞ −2 −1 0 +∞
f ′ + 0 − − 0 +
f
−∞
−3
−∞
+∞
1
+∞
-2 1O
y
x
-1
-3/2
x
y
O
-1 1-2
-3
2
3
1
1
-2
-3
-1
O
y
x
www.VNMATH.com

4. Chương I. Hàm s – Tr n Phương
102
b) ( )2
1 1 0x m x m+ − + − = ⇔ ( )
2
1
1
x x
f x m
x
+ +
= =
+
.
(C′): ( )y f x= ư c v t (C): y = f (x) theo qui t c: Gi nguyên ph n th (Ca)
c a (C) ng x ≥ 0. L y (C′a) i x ng v i (Ca) qua Oy, khi ó (C′) = (Ca) ∪ (C′a)
c) t [ ] [ ]sin 0,1 0,t x x= ∈ ∀ ∈ π . Khi ó ( )2
sin 1 sin 1 0x a x a− − + − =
⇔ ( )
2
1
1
t tf t a
t
+ += =
+
v i t ∈ [0, 1].
Bài 5. a. Kh o sát s bi n thiên và v th c a ( )
2
2( ):
1
x xC y f x
x
− += =
−
b. Tìm a phương trình:
2
2 1
1
x x ax a
x
− + = − +
−
có nghi m
c. Bi n lu n theo m s nghi m c a phương trình:
2
2
2
log
1
x x
m
x
− +
=
−
Gi i: a. ( )
( )
2 1
2
2
1 2
2 1 0
1 1 2
x x
x xf x
x x x
 = = −
− − ′ = = ⇔
− = = +
⇒
( )
( )
1
2
1 2 1 2 2
1 2 1 2 2
y f
y f
 = − = −

 = + = +
( ) 2
1
f x x
x
= +
−
⇒ TC : x = 1; TCX: y = x.
b. Nghi m c a
2
2 1
1
x x ax a
x
− + = − +
−
là
hoành giao i m c a ư ng th ng
(D): ( )1 1y a x= − + v i (C): y = f (x).
Do (D) luôn i qua i m c nh
I(1, 1) nên phương trình trên có
nghi m thì (D) ph i n m trong góc nh n
t o b i 2 ti m c n: TC : x = 1 (v i h
s góc k = +∞) và TCX: y = x (v i h
s góc k = 1) ⇒ a > 1
c. Do ( )
2
2
1
x x
y f x
x
− +
= =
−
là hàm
ch n nên th ( ) ( ):C y f x′ = nh n
Oy làm tr c i x ng và ư c v t
(C): y = f (x) theo qui t c:
x
21-
y
1+ 2
-2
1
21+2
1
O
O
1
1+2 2
1
-2
21+
y
x-1- 2
www.VNMATH.com

5. Bi n lu n phương trình, b t phương trình b ng th
103
Gi nguyên ph n th c a (C) ng v i x ≥ 0 r i l y i x ng ph n này qua Oy.
Nghi m c a phương trình ( ) 2logf x m= (m > 0) là hoành giao i m c a
ư ng th ng 2logy m= v i th (C′). Nhìn vào th ta có:
N u 2log 2m < − ⇔ 10
4
m< < thì phương trình có 2 nghi m. …
Bài 6. a. Kh o sát và v ( ) 4 2
2 3y f x x x= = − + +
b. Bi n lu n theo m s nghi m: 4 2 4 2
2 2x x m m− = −
Gi i
a. ( ) ( )3 2
4 4 4 1 0 0; 1f x x x x x x x′ = − + = − = ⇔ = = ± ⇒ C c tr (0, 3), (±1, 4)
( ) ( )2 2 112 4 4 1 3 0
3
f x x x x′′ = − + = − = ⇔ = ± ⇒ i m u n 321 ,
93
 ± 
 
b. ( ) ( )4 2 4 2 4 2 4 2
2 2 2 3 2 3x x m m x x m m f x f m− = − ⇔ − + + = − + + ⇔ = (*)
Nhìn vào th ta có:
N u ( ) 4 1f m m= ⇔ = ± thì (*) có 2 nghi m kép x = ±1.
N u ( ) ( ) { }3 4 2, 2 0, 1f m m< < ⇔ ∈ − ± thì (*) có 4 nghi m phân bi t.
N u ( ) { }3 0, 2f m m= ⇔ ∈ ± thì (*) có 3 nghi m x = 0; 2x = ± .
N u ( ) ( ) ( )3 , 2 2,f m m< ⇔ ∈ −∞ − +∞∪ thì (*) có 2 nghi m phân bi t.
Bài 7. a) Kh o sát và v th ( ) 3
( ): 4 3 1C y f x x x= = − −
b) Tìm m
3
4 3 1 0x x mx m− − + − = có 4 nghi m phân bi t.
Gi i
( ) 2 112 3 0
2
f x x x′ = − = ⇔ = ±
( ) 24 0 0f x x x′′ = = ⇔ =
⇒ C c i ( )1 ,0
2
− ; c c ti u ( )1 , 2
2
−
x −∞ −1 0 1 +∞
f ′ + 0 − 0 + 0 −
f
−∞
4
3
4
−∞
x −∞
1
2
− 1
2 +∞
f ′ + 0 − 0 +
f
−∞
0
−2
+∞
3- 3
O x
y
1-1
- 2 2
3
4
www.VNMATH.com

6. Chương I. Hàm s – Tr n Phương
104
i m u n U(0, −1)
b)
3
4 3 1 0x x mx m− − + − = ⇔ ( ) ( )3
4 3 1 1f x x x m x= − − = − (*)
th (C′): ( )y f x= ư c v t th (C): y = f (x) theo qui t c:
- Gi nguyên ph n th (Ca) c a (C) ng v i x ≥ 0.
- L y (Ca′) i x ng v i (Ca) qua Oy, khi ó (C′) = (Ca) ∪ (Ca′)
Nghi m c a (*) là hoành giao i m
c a ư ng th ng ( ) ( ): 1md y m x= −
v i th (C′): ( )y f x= .
Ta th y (dm) luôn i qua i m A(1, 0) ∈ (C′)
và (dm) qua B(0, −1) là (AB):
1y x= − có h s góc k1 = 1.
ư ng th ng c a h (dm) ti p xúc v i (Ca′)
t i i m có hoành x0 < 0 là nghi m c a phương trình:
( )
( )
3
2
2
2
4 3 1 1
3 1 4
x x k x
x k
 − + − = −

− =
⇒
( )( )3 2
4 3 1 3 1 4 1x x x x− + − = − −
⇔ ( ) ( )( )2 2
1 4 2 1 3 1 4 1x x x x x− + − = − −
⇔ ( )( )2
2 2 1 2 2 1 0x x x− − − = .
Do x0 < 0 nên 0
1 3
2
x
−
= ⇒ 2 6 3 9k = −
Nhìn vào th (C′) ta th y: phương trình có 4 nghi m phân bi t thì
( ) ( ): 1md y m x= − ph i c t th (C′): ( )y f x= t i 4 i m phân bi t ⇔
1 2k m k< < ⇔ 1 6 3 9m< < −
Bài 8. Tìm m 3
2 1m x x− + + = có 3 nghi m phân bi t.
Gi i
-2
y
xO
1/2 1-1/2
-1
-1
-1/2 11/2
O x
y
-2
-1
A
B
t
www.VNMATH.com

7. Bi n lu n phương trình, b t phương trình b ng th
105
t 2
2 0 2t x x t= + ≥ ⇒ = − , khi ó PT ⇔ 3 2
2 1m t t− + = −
( )32
2 1m t t⇔ − + = − ( ) 3 2
4 3 1f t t t t m⇔ = − + − − = .
Xét th (C): y = ƒ(t). Ta có: ( ) 2 4 7
3 8 3 0
3
f t t t t
±′ = − + − = ⇔ =
⇒ C c tr :
4 7 7 14 7
3 27
f
 ± − ±
= 
 
và ( )0 1f = − ⇒ Hình d ng th (C)
V i m i giá tr t ≥ 0 thì cho ta 1 nghi m
2
2x t= − nên PT ã cho có 3 nghi m
phân bi t thì ƒ(t) = m ph i có 3 nghi m
phân bi t t ≥ 0.
Nghi m c a ƒ(t) = m là hoành giao i m c a th y = ƒ(t) v i y = m.
Nhìn vào th ta có ƒ(t) = m có 3 nghi m phân bi t t ≥ 0
⇔ ( )4 7 7 14 7
0 1
3 27
f m f m
 − − −
< ≤ ⇔ < ≤ 
 
Bài 9. Tìm m PT: 2 2 2
sin sin 3 cos 2 0x x m x+ − = (*) có nghi m.
Gi i
( )2 21 cos 2 1 cos6 1(*) cos 2 1 cos6 cos 2 cos 2
2 2 2
x x m x x x m x− −⇔ + = ⇔ − + =
3 2
2cos 2 cos 2 1 cos 2x x m x⇔ − + + =
t [ ]cos 2 1,1t x= ∈ − , khi ó (*) ⇔ ( ) 3 2
2 1f t t t mt= − + + = .
Ta có: ( ) 2 16 1 0
6
f t t t′ = − + = ⇔ = ±
Nhìn vào th ta th y: (*) có nghi m ⇔ Parabol (Pm): 2
y mt= c t th
(C): y = ƒ(t) t i i m có hoành t∈[−1, 1] ⇔ m > 0
t −1
1
6
− 1
6
1
f ′ + 0 − 0 +
ƒ
2
CT
C
0
-1
O x
y
74+
3
3
4- 7
714
3
-7
-7
3
-14 7
y
xO
2
1
1
-1
www.VNMATH.com

8. Chương I. Hàm s – Tr n Phương
106
II. BI N LU N B T PHƯƠNG TRÌNH B NG TH
1. Các bài t p m u minh h a
Bài 1. Tìm m BPT: ( )( ) 2
4 6 2x x x x m+ − ≤ − + úng ∀x∈[−4, 6]
Gi i
t ( )( )
( )( )
( )
( )22 2
00
4 6 :
4 6 1 25
yy
y x x C
y x x x y
≥≥ 
= + − ⇔ ⇔ 
= + − − + =  
• (C) là n a ư ng tròn phía trên Ox
v i tâm I(1, 0), bán kính R = 5.
• ( ) 2
: 2mP y x x m= − + là 1 parabol có
nh D(1, m − 1) ∈ ư ng th ng x = 1.
Ta có: ( )( ) 2
4 6 2x x x x m+ − ≤ − + ∀x∈[−4, 6]
⇔ (C) n m phía dư i (Pm) ∀x∈[−4, 6]
⇔ nh T(1, 5) c a (C) n m dư i D(1, m − 1) ⇔ m − 1 ≥ 5 ⇔ m ≥ 6.
Bài 2. Cho BPT: ( ) 2
2 1 2 3x x m x x− + + ≥ − + (*)
a. Tìm m BPT (*) có nghi m
b. Tìm m dài mi n nghi m c a (*) b ng 2.
Gi i
Parabol (P): 2
2 3y x x= − + có nh D(1, 2)
G i (Cm): ( )2 1y x x m= − + + ⇔
( )2
2 1
0
y x x m
y
 = − + +

≥
⇔ (Cm):
( )2 2
0
1 2
y
x y m
≥

− + = +
v i m ≥ −2.
Ta có (Cm) là n a ư ng tròn phía trên Ox
v i tâm I(1, 0), bán kính 2R m= + và có
nh ( )T 1, 2m + .
a. BPT (*) có nghi m thì nh ( )T 1, 2m + ph i n m phía trên D(1, 2)
⇔ 2 2 2 4 2m m m+ ≥ ⇔ + ≥ ⇔ ≥
b. Gi s (Cm) ∩ (P) t i 2 i m phân bi t A1(x1, y0), A2(x2, y0)
O
y
x1-4 6
T
Dm-1
1 x
y
O
2 3
3
A
B
T
D
-1
www.VNMATH.com

9. Bi n lu n phương trình, b t phương trình b ng th
107
⇒ Mi n nghi m c a BPT (*) là [ ]1 2,x x ⇒ x2 − x1 = 2 (1)
Vì A1, A2∈(P) nên ta có x1, x2 là nghi m c a phương trình 2
02 3 0x x y− + − =
⇒ 1 2 2x x+ = , k t h p v i (1) ⇒ 1 20, 2x x= = ⇒ 0 3y =
⇒ ( )
2 2
1 02 1 1 9 10m x y+ = − + = + = ⇔ m = 8.
Bài 3. Tìm m BPT: ( )( ) 2
4 4 2 2 18x x x x a− − + ≤ − + − úng ∀x∈[−2, 4]
Gi i
( )( ) ( )( )
2
2 184 4 2 2 18 4 2
4 2 4
x x ax x x x a x x − −− − + ≤ − + − ⇔ − + ≥ + −
t ( )( )
( )( )
( )
( )22 2
00
4 2 :
4 2 1 9
yy
y x x C
y x x x y
≥≥ 
= − + ⇔ ⇔ 
= − + − + =  
• (C) là n a ư ng tròn phía trên
Ox v i tâm I(1, 0), bán kính R = 3.
• ( )
2
18:
4 2 4m
x x aP y − −= + − là m t
parabol quay b lõm xu ng dư i và
nh n x = 1 làm tr c i x ng.
• (C) ∩ Ox t i A(−2, 0) và B(4, 0) i x ng qua x = 1. Ta xét parabol (P) thu c
h (Pm) i qua A, B:
2
184 40 10
4 2 4
a a−−= + − ⇔ = ⇒ ( )
2
: 2
4 2
x xP y −= + +
Nhìn vào th suy ra (*) úng ∀x∈[−2, 4] thì a ≥ 10.
Bài 4. Cho BPT: ( ) 2
6 6 2x x x x m− ≥ − + + (*)
Tìm m dài mi n nghi m p c a (*) tho mãn: 2 ≤ p ≤ 4.
Gi i
t ( )
( )
( )
( )22 2
00
6 :
6 3 9
yy
y x x C
y x x x y
≥≥ 
= − ⇔ ⇔ 
= − − + =  
• (C) là n a ư ng tròn phía trên
Ox v i tâm I(3, 0), bán kính R = 3.
• ( ) 2
: 6 2mP y x x m= − + + là m t
parabol quay b lõm lên trên và
nh n x = 3 làm tr c i x ng.
A
-2
y
xO
1 4
B
O x
y
(P )1
2
(P )
C
A B
D
1 2
3
4 5 6
www.VNMATH.com

10. Chương I. Hàm s – Tr n Phương
108
Gi s (C) ∩ (Pm) t i 2 i m phân bi t M1(x1, y0), M2(x2, y0) v i x1 < x2.
⇒ M1, M2 i x ng v i nhau qua ư ng th ng x = 3 ⇒ 1 2 2.3 6x x+ = =
Nghi m c a BPT (*) là x∈[ ]1 2,x x ⇒ dài mi n nghi m p c a (*) là:
( )2 1 22 3p x x x= − = − . 2 ≤ p ≤ 4 thì 1 ≤ x2 − 3 ≤ 2 ⇔ 4 ≤ x2 ≤ 5
Xét các parabol P1, P2 thu c h (Pm) l n lư t qua ( ) ( )4,2 2 , 5, 5A B ∈(C) là
( ) 2
1 : 6 8 2 2P y x x= − + + và ( ) 2
2 : 6 5 5P y x x= − + +
Nhìn vào th suy ra (*) có dài mi n nghi m p tho mãn 2 ≤ p ≤ 4
thì 5 5 2 8 2 2 3 5 6 2 2m m+ ≤ + ≤ + ⇔ + ≤ ≤ +
Bài 5. Tìm m BPT: ( )2
2 2 3x x m− + − ≥ úng x∀ ∈»
Gi i
( )2
2 2 3x x m− + − ≥ ⇔
( )2 23 2 12
2 2 2
x xx m x m x
− − −− ≥ ⇔ − ≥ + −
Parabol
2
1( ): 2
2 2
xP y x−= + − quay b lõm xu ng dư i.
th ( )D :m y x m= − là hình v
ch V nh M(m, 0) g m 2 n a
ư ng th ng n m phía trên Ox và
t o v i Ox các góc 45° và 135°.
Xét nhánh ph i c a (Dm) ti p xúc v i (C), khi ó hoành ti p i m là nghi m
c a:
21 12 1
2 2
01 2
x m x x x
mx
− − = + − = 
⇔ 
= = − +
⇒ ( )0D : y x= ti p xúc (C)
Xét nhánh trái c a (Dm) ti p xúc v i (C), khi ó hoành ti p i m là nghi m
c a:
21 12 3
2 2
41 2
x m x x x
mx
−− + = + − = 
⇔ 
= − = − +
⇒ ( )4D : 4y x= − ti p xúc (C)
Nhìn vào th ta có: BPT úng ∀x ⇔ nh M(m, 0) c a (Dm) n m bên trái
nh (0, 0) c a (D0) ho c n m bên ph i nh (4, 0) c a (D4) ⇔ m ≤ 0 ho c m ≥ 4.
y
xO
1
1 2 3 4
3/2
www.VNMATH.com

11. Bi n lu n phương trình, b t phương trình b ng th
109
Bài 6. Gi i bi n lu n BPT: 2
5 4x x a− + <
Gi i
( )
( )
[ ]
2
2
2
5 4 khi 1,4
: 5 4
5 4 khi 1,4
x x x
C y x x
x x x
 − + ∈
= − + = 
− + − ∈
»
G i (C1) là ph n th n m phía trên tr c hoành c a 2
5 4y x x= − + còn (C2) là
ph n th i x ng qua Ox v i ph n th n m phía dư i Ox c a 2
5 4y x x= − +
Khi ó (C) = (C1) ∪ (C2). Xét ( ) ( ) 2
1 : 5 4C y a x x a= − + =∩
⇔ 1 2
5 9 4 5 9 4
;
2 2
a a
x x x x
− + + +
= = = =
Xét ( ) ( ) 2
2 : 5 4 0C y a x x a= − + + =∩
⇔ 3 4
5 9 4 5 9 4
;
2 2
a a
x x x x
− − + −
= = = =
Nhìn vào th ta có:
N u a ≤ 0 thì BPT vô nghi m.
N u 90
4
a< ≤ thì BPT có nghi m x∈(x1, x3) ∪ (x4, x2)
N u 9
4
a > thì BPT có nghi m x∈(x1, x2)
Bài 7. 1) Kh o sát và v (C): ( )
2
2 1
1
x xy f x
x
+ += =
−
2) Tìm s a nh nh t ( ) ( )22 2
1 1a x x x x+ − ≤ + + úng ∀x∈[0, 1]
Gi i
1) ( ) 43
1
f x x
x
= + +
−
⇒
TCÐ: 1
TCX : 3
x
y x
=

= +
( )
( )2
1 041 0
3 81
x y
f x
x yx
= − ⇒ =
′ = − = ⇔ 
= ⇒ =− 
x −∞ −1 1 3 +∞
f ′ + 0 − − 0 +
f
−∞
0
−∞
+∞
8
+∞
45/21
y
xO
4
9/4
-9/4
y=a
www.VNMATH.com

12. Chương I. Hàm s – Tr n Phương
110
2) t [ ] [ ]2
0,2 0,1t x x x= + ∈ ∀ ∈
( ) ( )22 2
1 1a x x x x+ − ≤ + + ∀x∈[0, 1]
( ) ( )2
1 1a t t⇔ − ≤ + ∀t∈[0, 2]
⇔
( ) ( ]
( ) [ )
1,2
0,1
f t a t
f t a t
 ≥ ∀ ∈

≤ ∀ ∈
⇔
( ]
( )
[ )
( )
1,2
0,1
Min
Max
t
t
f t a
f t a
∈
∈
 ≥


≤

( )
( )
2 9
0 1
f a
f a
 = ≥
⇔ 
= − ≤
⇔ −1 ≤ a ≤ 9.
V y s a nh nh t ( ) ( )22 2
1 1a x x x x+ − ≤ + + úng ∀x∈[0, 1] là a = −1.
Bài 8. 1) Kh o sát và v (C): ( )
2
3 3
2
x xy f x
x
− += =
−
2) Tìm s a l n nh t ( )2
6 12 4 2x x a x− + ≥ − úng ∀x∈[4, 5]
Gi i
1) ( ) 11
2
f x x
x
= − +
−
⇒
TCÐ: 2
TCX: 1
x
y x
=

= −
( )
( )2
1 111 0
3 32
x y
f x
x yx
= ⇒ = −
′ = − = ⇔ 
= ⇒ =− 
2) ( )2
6 12 4 2x x a x− + ≥ − ∀x∈[4, 5]
⇔
( )
2
6 12
4 2
x x a
x
− + ≥
−
∀x∈[4, 5]
⇔
2
3 3 3
2 4
x x x a
x
− + ≥ +
−
∀x∈[4, 5]
⇔ ư ng th ng (d): 3
4
y x a= +
n m phía dư i (C) ∀x∈[4, 5]
Xét ( ) ( )23 2 4
4
f x x′ = ⇔ − = [ ]4 4;5x⇔ = ∈
⇒ Phương trình ti p tuy n c a (C) song song v i (d) là:
(D): ( ) ( )3 3 14 4
4 4 2
y x f x= − + = + . Nhìn hình v suy ra:
S a l n nh t ( )2
6 12 4 2x x a x− + ≥ − úng ∀x∈[4, 5] là 1
2
a =
y
O-3
8
x1-1 32
-1
9
3
x −∞ 1 2 3 +∞
f ′ + 0 − − 0 +
f
−∞
−1
−∞
+∞
3
+∞
-1
2
3
3
O
x
y
1
(D)
4 5
www.VNMATH.com

13. Bi n lu n phương trình, b t phương trình b ng th
111
III. BI N LU N H PHƯƠNG TRÌNH B NG TH
1. Phương pháp chung
Bi u di n các i u ki n b ng ngôn ng hình h c và xét tính tương giao
Nghi m c a h là giao i m c a các ư ng cong bi u di n các i u ki n
2. Các bài t p m u minh h a
Bài 9. Tìm a h
( )
( )
2 2
2
2 1
4
x y a
x y
 + = +

+ =
có úng 2 nghi m.
Gi i
N u a < −1 thì h vô nghi m.
Xét a ≥ −1: ( ) ( )2 2
: 2 1aC x y a+ = + là ư ng
tròn tâm O(0, 0) bán kính ( )2 1R a= + .
( )2
4x y+ = ⇔ x + y = ±2.
Nghi m c a h ã cho chính là to c a các giao i m do ư ng th ng
( )1 : 2 0x y∆ + + = và ( )2 : 2 0x y∆ + − = c t (Ca).
Do (∆1), (∆2) i x ng nhau qua O nên h ã cho có úng 2 nghi m
⇔ (∆1), (∆2) ti p xúc (Ca) ⇔ ( )( ) ( )1O, 2 1 2 0R d a a= ∆ ⇔ + = ⇔ =
Bài 10. Cho h phương trình:
2 2
0
0
x ay a
x y x
+ − =

+ − =
a. Tìm a h có 2 nghi m phân bi t.
b. G i ( ) ( )1 1 2 2, , ,x y x y là các nghi m c a h .
CMR: ( ) ( )
2 2
2 1 2 1 1x x y y− + − ≤ . D u b ng x y ra khi nào?
Gi i
( ) ( )
( ) ( )
2
2 2 2
: 1 0
0
1 10 :
2 4
a x a y
x ay a
x y x C x y
 ∆ + − =
+ − = 
⇔ 
+ − = − + =

(C) là ư ng tròn tâm ( )1 ,0
2
I bán kính 1
2
R =
(∆a) là ư ng th ng quay quanh i m A(0, 1) c nh.
a. h có 2 nghi m phân bi t thì (∆a) c t (C) t i 2 i m phân bi t
( )1∆
∆2( )
xO
y
2
2
-2
-2
y
O x1
I
1
M
N
2
A
www.VNMATH.com

14. Chương I. Hàm s – Tr n Phương
112
⇔ ( )( ) ( )2
2
22 2
1
1 22 1 4, 1 3 4 0 0
2 311
a
a
a
d I R a a a
aa
−
−
∆ < ⇔ < ⇔ < ⇔ − < ⇔ < <
++
b. V i 40
3
a< < thì ư ng th ng (∆a) c t (C) t i 2 i m phân bi t
( )1 1M ,x y , ( )2 2N ,x y ⇒ 2MN R≤ =1 ( ư ng kính là dây l n nh t)
⇔ ( ) ( )
2 2
2 1 2 1 1x x y y− + − ≤ ⇒ ( pcm)
D u b ng x y ra ⇔ MN = 2R ⇔ (∆a) i qua ( )1 ,0
2
I ⇔ 1
2
a =
Bài 11. Tìm a h
1 2
3
x y a
x y a
 + + + =

+ =
có nghi m.
Gi i
N u a < 0 thì h vô nghi m. Xét a ≥ 0:
t
1 0
2 0
u x
v y
 = + ≥

= + ≥
. H ⇔
( )2 2
, 0
3 1
u v
u v a
u v a
≥

+ =

+ = +
( ) ( )2 2
: 3 1C u v a+ = + là h các ư ng tròn tâm O(0, 0) bán kính ( )3 1R a= +
( ):d u v a+ = là h các ư ng th ng // v i nhau t o v i Ou góc 135°
Xét ư ng th ng ( )1( ): 3 1d u v a+ = + i qua A(R, 0); B(0, R) ∈(C)
và ư ng th ng ( )2( ): 6 1d u v a+ = + ti p xúc v i (C) t i M
Nhìn vào th ⇒ h có nghi m thì (d) c t (C) t i i m có t a dương
⇔ (d) n m gi a (d1) và (d2) ⇔ ( ) ( )3 1 6 1a a a+ ≤ ≤ +
⇔
2
2
3 3 0 3 21
3 15
26 6 0
a a
a
a a
 − − ≥ +
⇔ ≤ ≤ +
− − ≤
Bài 12. Tìm m h
2 2
1 1 1x y
x y m
 − + + =

+ =
có 4 nghi m phân bi t.
3a+3
v
O u
3a+3
6a+6
6a+6
www.VNMATH.com

15. Bi n lu n phương trình, b t phương trình b ng th
113
Gi i
( ): 1 1 1L x y− + + = ⇔
[ ] [ ]
[ ] [ ]
[ ] [ ]
[ ] [ ]
1 0 1,2 , 1,0
3 0 1,2 , 2, 1
1 0 0,1 , 2, 1
1 0 0,1 , 1,0
x y x y
x y x y
x y x y
x y x y
 + − = ∈ ∈ −

 − − = ∈ ∈ − −

 + + = ∈ ∈ − −

− + + = ∈ ∈ −
víi
víi
víi
víi
• (L) có hình bi u di n là 4 c nh c a hình vuông
ABCD v i A(1, 0); B(2, −1); C(1, −2); D(0, −1)
• ( ) 2 2
:C x y m+ = là ư ng tròn tâm O(0, 0) bán
kính R m= .
Xét ư ng tròn tâm O ti p xúc v i BC có bán kính là: ( )1
3,( )
2
R d O BC= =
ư ng tròn tâm O i qua 2 i m B, C có bán kính là: 2 5R OC= = .
Nhìn vào th ta có: H có 4 nghi m phân bi t ⇔ (L) c t (C) t i 4 i m.
⇔ 1 2
3 95 5
22
R R R m m< < ⇔ < < ⇔ < <
Bài 13. Cho 2 2
1 và 6a b c d+ = + = . CMR: 2 2
2 2 18 6 2c d ac bd+ − − ≥ − (1)
Gi i
Trên m t ph ng t a l y M(a, b) và N(c, d) ⇒ ( ) ( )2 22
MN c a d b= − + −
và M n m trên ư ng tròn ( ) 2 2
: 1C x y+ = ; N n m trên (∆): 6x y+ =
Khi ó (1) ⇔ 2
MN 19 6 2 MN 3 2 1≥ − ⇔ ≥ −
G i kho ng cách t O n (∆) là: ( )O,d ∆
Ta có: ( )OM MN ON O,d+ ≥ ≥ ∆
⇒ ( ) 2 2
0 0 6
1 MN O, 3 2
1 1
d
+ −
+ ≥ ∆ = =
+
⇒ MN 3 2 1≥ − ( pcm)
D u b ng x y ra ⇔ M ∈ o n ON và ON ⊥ (∆) ⇔ 1
2
a b= = ; 3c d= =
xO
y
D
A
B
C
O
y
6
6
M
N
1 x
www.VNMATH.com

16. Chương I. Hàm s – Tr n Phương
114
IV. BI N LU N H B T PHƯƠNG TRÌNH B NG TH
Bài 1. Cho h b t phương trình:
2
2
2 0
4 6 0
x x a
x x a
 + + ≤

− − ≤
a. Tìm a h có nghi m. b. Tìm a h có nghi m duy nh t.
Gi i
( )
( )
2
2
2
2
22 0
44 6 0
6
a f x x xx x a
x xa g xx x a
 ≤ = − − + + ≤ 
⇔  −≥ =− − ≤  
(P1): y = f (x) là 1 parabol quay b lõm
xu ng dư i và có nh là (−1, 1)
(P2): y = g(x) là 1 parabol quay b lõm lên trên và c t (P1) t i 80;
7
x x −= =
a. H ã cho có nghi m ⇔ ư ng th ng y = a i qua mi n g ch chéo t o b i
(P1) và (P2) ⇔ 0 ≤ a ≤ 1.
b. H ã cho có nghi m duy nh t ⇔ ư ng th ng y = a c t mi n g ch chéo t i
m t i m duy nh t ⇔ a = 0 ho c a = 1.
Bài 2. Tìm m BPT: ( )2
1
2
log 2 3x x m− + > − (1) có nghi m
và m i nghi m u ∉ TX c a ( )3
1log 1 .log 2x xy x x+= + − (2)
Gi i
• TX c a (2) là nghi m c a h :
( ) ( ) ( )23 3
1
0 10 1
2
log 1 2 1 1x
xx
x
x x x+
< ≠< ≠  
⇔ ⇔ ≥ 
+ ≥ + ≥ +  
• ( )2
1
2
log 2 3x x m− + > − ⇔ 2
0 2 8x x m< − + <
⇔
( ) ( )
( ) ( )
2
1
2
2
2 :
2 8 :
m x x f x y P
m x x g x y P
 > − + = =

< − + + = =
ư ng th ng y = m i qua mi n g ch chéo t o b i (P1) và (P2) ⇔ m ≤ 9.
M i nghi m c a (1) u ∉ TX c a (2) ⇔ M i nghi m x c a (1) u < 2
⇔ Hình chi u c a o n th ng giao gi a y = m v i mi n g ch chéo lên Ox là
t p con c a kho ng (−∞, 2). T th duy ra 8 ≤ m ≤ 9.
y
O
x-1
-2 2 4
1
-2/3
9
-2
21 x
8
O
y
4
www.VNMATH.com

17. Bi n lu n phương trình, b t phương trình b ng th
115
Bài 3. Tìm m h
2
4 2
2 4 0
6 8 18 0
x x m
x x x m
 − − + ≤

− − + − ≤
(*) có nghi m.
Gi i
H
2
4 2
2 4 0
6 8 18 0
x x m
x x x m
 − − + ≤

− − + − ≤
( )
( )
2
4 2
2 4
6 8 18
m f x x x
m g x x x x
 ≤ = − + +
⇔ 
≥ = − − +
(P): y = f (x) là 1 parabol quay b lõm xu ng dư i và có nh là D(1, 5)
• Xét (C): y = g(x).
Ta có: ( ) ( ) ( )23
4 12 8 4 1 2g x x x x x′ = − − = + −
Xét (C) ∩ (P): ( ) ( )g x f x=
( )( )3 2
1 4 14 0x x x x⇔ − + − − = ⇔ ( ) 3 2
1 4 14 0x h x x x x= ∨ = + − − =
Do ( ) ( )2 6; 3 10h h= − = nên (C) ∩ (P) t i x1 = 1 và x2∈(2, 3)
Nhìn vào th ta có h (*) có nghi m ⇔ ư ng th ng y = m i qua mi n
g ch chéo t o b i (P) và (C) ⇔ −6 ≤ m ≤ 5.
Bài 4. Tìm a ( )2 1 2x y x y a+ + − + = (*)
có nghi m.
Gi i
(*) ( ) ( )2 1 2x y a x y⇔ − + = − +
( ) ( )
2
2
2 1 2
x y
x y a x y
+ ≤

⇔ 
 − + = − +  
( ) ( )22
2 0
1 2 1
x y
x y a
+ − ≤
⇔ 
− + − = +
( ) ( ) ( )22
: 1 2 1C x y a− + − = + là ư ng tròn tâm I(1, 2) bán kính 1R a= +
x −∞ −1 2 +∞
f ′ − 0 − 0 +
f
+∞
−6
+∞
y
O x1
2 51+1- 5
-6
5
I
2
2
1 xO
y
www.VNMATH.com

18. Chương I. Hàm s – Tr n Phương
116
Nghi m c a (*) là giao c a ư ng tròn (C) v i mi n g ch chéo n m phía dư i
ư ng th ng (∆): x + y − 2 = 0.
(*) có nghi m thì ( )( ) 2 2
1 2 2 1 1, 1 1
2 21 1
d I R a a a
+ − −∆ ≤ ⇔ ≤ + ⇔ ≤ + ⇔ ≥
+
Bài 5. Tìm m h
( )2 2log 1 (1)
2 (2)
x y
x y
x y m
+
 + ≥

 + =
có nghi m.
Gi i
(1) ⇔
2 2
2 2
1
0
1
x y x y
x y
x y x y
 + ≥ + >

 + >

 + ≤ + <
⇔
( ) ( ) ( ) ( )
2 2
2 2
2 2
2 2
1
1
0
1 1 1
1 1 12 2 2
2 2 2
x y
x y
x y
x y
x y
 + <
 + > 
  + >
∨ 
− + − ≤ 
 − + − ≥

( ) 2 2
1 : 1C x y+ = là ư ng tròn tâm O(0, 0) bán kính 1 1R =
( ) ( ) ( )
2 2
2
1 1 1:
2 2 2
C x y− + − = là ư ng tròn tâm ( )1 1,
2 2
I bán kính 2
1
2
R =
(d): x + y = 0 c t (C1) t i 1 1 1 1, ; ,
2 2 2 2
A B− −   
   
   
. Nghi m c a (1) là mi n
g ch chéo (hình v ) trong ó không l y biên c a (C1) nhưng l y biên c a (C2).
Xét ư ng th ng thu c h (∆m): x + 2y = m i qua A là (∆1): 12
2
x y −+ =
ư ng th ng thu c h (∆m) ti p xúc v i (C2)
⇔ ( ) 2, md I R∆ =
2 2
1 1
2 1
21 2
m+ −
⇔ =
+
10 3 103
2 2 2
m m
±
⇔ − = ⇔ =
⇒ ư ng th ng (∆2):
3 10
2
2
x y
+
+ =
n m phía trên và ti p xúc v i (C2).
(*) có nghi m thì (∆m) c t mi n g ch chéo
⇔ (∆m) n m gi a (∆1) và (∆2) ⇔
3 101
22
m
+− < ≤
O
x
y
I
1
11/2
1/2
A
(D )1
2
(D )
www.VNMATH.com