1. 一般化線形混合モデル
GLIMMIX
東京大学医学系研究科
M1 倉橋 一成
1

2. 4.Computational Aspects
コンピュータ計算をする際の問題点
分散の初期値：共分散は0，分散は小さな値
分散パラメータが負になるときの対処
two-level problem（Lamotte 1972）
作業行列Yの計算方法
2

3. 5.Simulation Study
以下のモデルによりデータを発生
logit E ( ykl bk ) = α 0 + α1tl + α 2 xk + α 3 xk tl + bk0 + bk t1
1
1 0  .50 0 
= = 
D1  or D2 
 0 0  0 .25 
k ：個人 ( k = 1,...,100 )
l ：繰り返し ( l = 1,..., 7 )
x ：グループ ( x
= k 1= 1,...,50 k 0 otherwise )
if k = ,x
y：二項結果変数
m ：試行回数 ( m = 1, 2, 4,8)
D ：変量効果ベクトルの共分散行列 ( D1 → 200, D1 → 100 ) 3

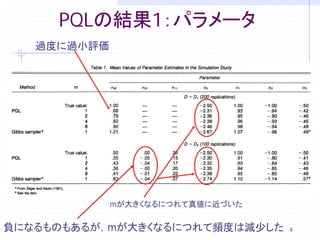
4. PQLの結果1：パラメータ
過度に過小評価
mが大きくなるにつれて真値に近づいた
負になるものもあるが，mが大きくなるにつれて頻度は減少した 4

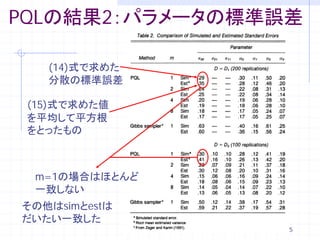
5. PQLの結果2：パラメータの標準誤差
(14)式で求めた
分散の標準誤差
(15)式で求めた値
を平均して平方根
をとったもの
m=1の場合はほとんど
一致しない
その他はsimとestは
だいたい一致した
5

6. MQLの結果
(18)式の近似の良さを調べたい
平均構造のモデルを誤特定したときの
共分散行列の歪み具合を知りたい
Balanced design→MQLとロジスティック
回帰での固定効果の推定値は等しい
D1の状況：近似は良さそう
σ σ
D2の状況： 00を過大推定， 01はしばしば負
→係数の符号が逆であることが原因
6

7. これまでの復習
混合モデルの記述に2通りの方法がある
1.階層モデル
2.周辺モデル
Breslow and ClaytonはそれぞれPQLと
MQLによるパラメータ推定を提案
→実際にSASで使われている解析方法を
簡単に紹介
7

8. 例：Hessian Flyの畑への影響
畑を4ブロックに分割し，各ブロックを4×4分割
i ：block（4ブロック）
j：entry（16種）
nij ：その区画に生息する小麦の数(n)
Yij ：害を受けた小麦の数(Y)
生物統計データでは：entry→人？
block→時点？
8

9. データセット
data HessianFly;
label Y = ’No. of damaged plants’
n = ’No. of plants’;
input block entry lat lng n Y @@;
datalines;
1 14 1 1 8 2 1 16 1 2 9 1 1 7 1 3 13 9 1 6 1 4 9 9
1 13 2 1 9 2 1 15 2 2 14 7 1 8 2 3 8 6 1 5 2 4 11 8
1 11 3 1 12 7 1 12 3 2 11 8 1 2 3 3 10 8 1 3 3 4
12 5
1 10 4 1 9 7 1 9 4 2 15 8 1 4 4 3 19 6 1 1 4 4 8 7
・・・
9

10. 解析1：一般化線形モデル
(GLM)
仮定
害の受けやすさはそれぞれ独立
同じ区画内の小麦は同じくらい害を受けやすい
→ Yij は独立に二項分布に従う
 一般化線形モデルでの解析
E Yij  =
  ( )
164 I 4 ⊗ 116 14 ⊗ I16 β, βT = ( µ , βb1 ,..., βb 4 , β e1 ,..., β e16 )
n×m r×c nr×mc
 a11  a1m   b11  b1c   a11 B  a1m B 
     
ただし，A =    , B      のとき，A ⊗ B = 
    である．
a  a  b  b  a B  a B
 n1 nm   r1 rc   n1 nm 
10

11. SASプログラム(GLM)
proc glimmix data=HessianFly;
class block entry;
model y/n =block entry / solution;
run;
class statement：block，entry
model statement：結果変数→二項分布
リンク関数→logit
オプションにdist=binomial link=logitを挿入しても同じ
11

12. 結果：model
The GLIMMIX Procedure
Model Information
Data Set WORK.HESSIANFLY
Response Variable (Events) Y
Response Variable (Trials) n
Response Distribution Binomial
Link Function Logit
Variance Function Default
Variance Matrix Diagonal
Estimation Technique Maximum Likelihood
Degrees of Freedom Method Residual
検定の自由度はresidual法で計算
→オブザベーション数から計画行列のランクを引く方法
DDFMオプションで変更可能 12

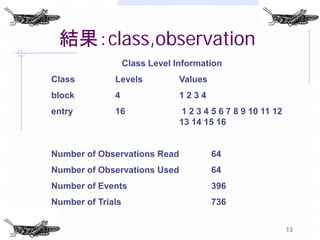
13. 結果：class,observation
Class Level Information
Class Levels Values
block 4 1234
entry 16 1 2 3 4 5 6 7 8 9 10 11 12
13 14 15 16
Number of Observations Read 64
Number of Observations Used 64
Number of Events 396
Number of Trials 736
13

14. 結果：dimension
Dimensions
Columns in X 21
Columns in Z 0
Subjects (Blocks in V) 1
Max Obs per Subject 64
計画行列 X ：切片，block×4，entry×16
14

15. 結果：optimization
Optimization Information
Optimization Technique Newton-
Raphson
Parameters in Optimization 19
Lower Boundaries 0
Upper Boundaries 0
Fixed Effects Not Profiled
デフォルト：Newton-Raphson法
T
X X のランク数だけのパラメータを推定
15

16. 結果：iteration
Iteration History
Objective Max
IterationRestarts Evaluations Function Change
Gradient
0 0 4 134.13393738 . 4.899609
1 0 3 132.85058236 1.28335502 0.206204
2 0 3 132.84724263 0.00333973 0.000698
3 0 3 132.84724254 0.00000009 3.029E-8
Convergence criterion (GCONV=1E-8) satisfied.
change：目的関数の変化
16

17. 結果：fit statistics
Fit Statistics
-2 Log Likelihood 265.69
AIC (smaller is better) 303.69
AICC (smaller is better) 320.97
BIC (smaller is better) 344.71
CAIC (smaller is better) 363.71
HQIC (smaller is better) 319.85
Pearson Chi-Square 106.74
Pearson Chi-Square / DF 2.37
-2 Log Likelihoodはnested modelを比較する際に有
用
その他はnonnested modelを比較する際に有用
17

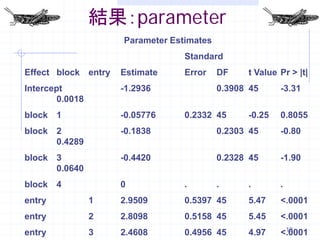
18. 結果：parameter
Parameter Estimates
Standard
Effect block entry Estimate Error DF t Value Pr > |t|
Intercept -1.2936 0.3908 45 -3.31
0.0018
block 1 -0.05776 0.2332 45 -0.25 0.8055
block 2 -0.1838 0.2303 45 -0.80
0.4289
block 3 -0.4420 0.2328 45 -1.90
0.0640
block 4 0 . . . .
entry 1 2.9509 0.5397 45 5.47 <.0001
entry 2 2.8098 0.5158 45 5.45 <.0001
18
entry 3 2.4608 0.4956 45 4.97 <.0001

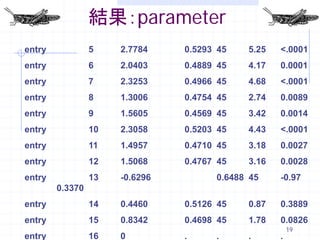
19. 結果：parameter
entry 5 2.7784 0.5293 45 5.25 <.0001
entry 6 2.0403 0.4889 45 4.17 0.0001
entry 7 2.3253 0.4966 45 4.68 <.0001
entry 8 1.3006 0.4754 45 2.74 0.0089
entry 9 1.5605 0.4569 45 3.42 0.0014
entry 10 2.3058 0.5203 45 4.43 <.0001
entry 11 1.4957 0.4710 45 3.18 0.0027
entry 12 1.5068 0.4767 45 3.16 0.0028
entry 13 -0.6296 0.6488 45 -0.97
0.3370
entry 14 0.4460 0.5126 45 0.87 0.3889
entry 15 0.8342 0.4698 45 1.78 0.0826
19
entry 16 0 . . . .

20. 結果：test
Type III Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
block 3 45 1.42 0.2503
entry 15 45 6.96 <.0001
固定効果に対するWald流の検定
entry効果が有意
→entry間で害の受けやすさが異なる
20

21. 解析2：一般化線形混合モデル
（階層モデル）
過大分散の原因：
 二項分布がfitしてない？
 重要な主効果が抜けている？
 観測値が相関している？
→まずはblock効果を変量効果と考えたモデル
E Yij =
   (164 14 ⊗ I16 ) β + ( I 4 ⊗ 116 ) b
βT (= ( b1 ,..., b4 )
µ , β e1 ,..., β e16 ) , bT
21

22. SASプログラム(階層モデル)
proc glimmix data=HessianFly;
class block entry;
model y/n = entry / solution;
random block;
run;
block効果を変量効果と考えたモデル
結果変数は二項分布を仮定
22

23. 結果：model，dimension
Estimation Technique Residual PL
Degrees of Freedom Method Containment
条件付モデルの場合はREMLを使用する
Columns in X 17
Columns in Z 4
計画行列 X：切片，entry×16
Z ：block×4 23

24. 結果：optimization
Optimization Technique Dual Quasi-
Newton
Parameters in Optimization 1
GLMMではQuasi-Newton法がデフォルト
この方法は二次導関数を必要としない
共分散を指定していない
→Dual Quasi-Newton法
24

25. 結果：covariance
Cov Standard
Parm Estimate Error
block 0.01116 0.03116
block効果の分散はかなり小さい
→block要因単独では過大分散に対処でき
ていない
25

26. 結果：parameter
Standard
Effect entry Estimate Error DF t Value Pr > |t|
Intercept -1.4637 0.3738 3 -3.92
0.0296
entry 1 2.9609 0.5384 45 5.50 <.0001
entry 2 2.7807 0.5138 45 5.41 <.0001
entry 3 2.4339 0.4934 45 4.93 <.0001
…
変量効果の影響で全体的に減少傾向
26

27. 解析3：一般化線形混合モデル
（周辺モデル）
周辺モデルによって共分散構造を直接指定
proc glimmix data=HessianFly;
class entry;
model y/n = entry / solution ddfm=contain;
random _residual_ / subject=intercept
type=sp(exp)(lng lat);
run; 測定誤差行列を指定
全観測値が相関していると仮定
27

28. 結果：covariance
Cov Parm Subject Estimate Error
SP(EXP) Intercept 0.9052 0.4404
Residual 2.5315 0.6974
SP(EXP)は3倍する→3 × 0.9052 =
2.7156
この値はblock内の相関を表している
この相関を考慮した分散が2.5315であ
る
28

29. 結果：test
Num Den
Effect DF DF F Value Pr
>F
entry 15 48 3.60 0.0004
F値は大幅に減少しており，過大分散を
考慮できていると考えられる
29

30. 簡単なまとめ
相関のあるデータを解析する場合の
過大分散に対処するためのモデル
1.G-side random effects models（階層モデ
ル）
2.R-side spatial covariance structure models
（周辺モデル）
2つのモデルでは結果が異なる
リンク関数がidenticalな場合は同じ結果となる
30

31. 6.4 Mixed Model for the Log Odds Ratio
小児癌の研究(Oxford S)
 Oxford Survey of Childhood Cancers(ORCC)
 RF:妊娠期の放射線（X-ray）の曝露
 コホート期間：1953-65
 小児癌での死亡年齢：0-9
120個の2×2表をもとに各オッズ比を計算
粗解析（Zelen 1971）
 死亡年齢（j）ではオッズ比はほぼ等しい
 出生年（k）ではオッズ比が異なる
Kneale(1971) Biometrics,27,563-90
31

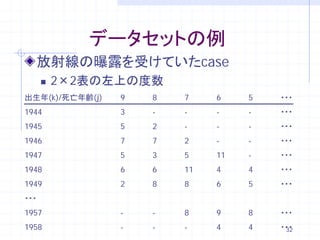
32. データセットの例
放射線の曝露を受けていたcase
 2×2表の左上の度数
出生年(k)/死亡年齢(j) 9 8 7 6 5 ・・・
1944 3 - - - - ・・・
1945 5 2 - - - ・・・
1946 7 7 2 - - ・・・
1947 5 3 5 11 - ・・・
1948 6 6 11 4 4 ・・・
1949 2 8 8 6 5 ・・・
・・・
1957 - - 8 9 8 ・・・
1958 - - - 4 4 ・・・
32

33. SASデータセット
data OSCC;
input cohort aad case ray weight @@;
cards;
X-ray（曝露）
1944 9 1 1 3.5 1944 9 0 1 0.5
age at death
1944 9 1 0 25.5 1944 9 0 0 28.5
1945 9 1 1 5 1945 9 0 1 2
1945 9 1 0 16 1945 9 0 0 19 出生年
1945 8 1 1 2 1945 8 0 1 2
1945 8 1 0 30 1945 8 0 0 30
…
非曝露群のコントロールが
0だったので0.5を加えた 33

34. モデル
1.相対リスクを出生年(k)毎に推定
logψ jk = α k
2.出生年の固定効果と変量効果を考慮
logψ jk = + β1Yeark + β 2 (Yeark2 − 22 ) + σµk , µk ~ N ( 0,1) , i.i.d .
α
3.出生年の変量効果に自己回帰構造を想定
 1 −2 1 0 0 0 
 
 −2 5 −4 1 0 0 
logψ jk = 1Yeark + σµk ,
α +β μT Rμ = μT  1 −4 6 −4 1 0  μ
 
 0 1 −4 6 −4 1 
      
 
34

35. 結果（モデル1）
35

36. 結果（モデル1）
外れ値の影響で二次曲線の
当てはまりが良いのでは？
36

37. 試行錯誤1（WLS）
重み付き最小二乗法（WLS） 重み（分散）を作る
変量効果無し
data out3;
set out3; Mixedで推定した値
_alpha=0.59; _beta1=-0.05; _beta2=-0.006; 固定効果
_myu=exp(_alpha+_beta1*year+_beta2*year2);
_weight=1/(N/(N-1)/((1/_myu)+(1/(_myu+n1-m1))+(1/(m1-myu))+(1/(n2-
_myu))));
run;
proc nlmixed data=out3;
myu=alpha+beta1*year+beta2*year2;
ll=-((logrr-myu)**2)*_weight;
対数尤度
model logrr ~ general(ll);
結果変数がこの対数尤度に従うと指定
run;
37
対数オッズ比

38. 思考錯誤2（IWLS）
繰り返し重み付き最小二乗法（IWLS）
変量効果無し
固定効果をモデル化
proc nlmixed data=out3;
myu=alpha+beta1*year+beta2*year2;
weight=1/(N/(N-1)/((1/exp(myu))+
(1/(exp(myu)+n1-m1))+(1/(m1-exp(myu)))+(1/(n2-exp(myu)))));
ll=-((logrr-myu)**2)*weight;
初期値を設定
model logrr ~ general(ll);
parms alpha=0.58 beta1=-0.051 beta2=0;
run;
→WLS,IWLS共にGauss-Hermite quadratureで最適化38

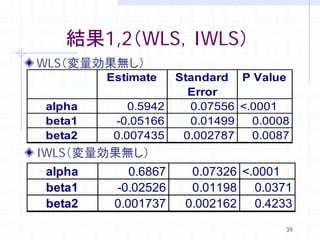
39. 結果1,2（WLS，IWLS）
WLS（変量効果無し）
Estimate Standard P Value
Error
alpha 0.5942 0.07556 <.0001
beta1 -0.05166 0.01499 0.0008
beta2 0.007435 0.002787 0.0087
IWLS（変量効果無し）
alpha 0.6867 0.07326 <.0001
beta1 -0.02526 0.01198 0.0371
beta2 0.001737 0.002162 0.4233
39

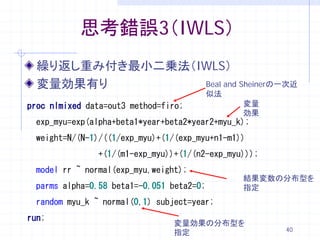
40. 思考錯誤3（IWLS）
繰り返し重み付き最小二乗法（IWLS）
変量効果有り Beal and Sheinerの一次近
似法
proc nlmixed data=out3 method=firo; 変量
効果
exp_myu=exp(alpha+beta1*year+beta2*year2+myu_k);
weight=N/(N-1)/((1/exp_myu)+(1/(exp_myu+n1-m1))
+(1/(m1-exp_myu))+(1/(n2-exp_myu)));
model rr ~ normal(exp_myu,weight);
結果変数の分布型を
parms alpha=0.58 beta1=-0.051 beta2=0; 指定
random myu_k ~ normal(0,1) subject=year;
run;
変量効果の分布型を
40
指定

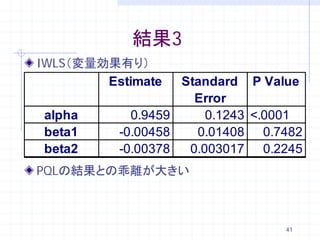
41. 結果3
IWLS（変量効果有り）
Estimate Standard P Value
Error
alpha 0.9459 0.1243 <.0001
beta1 -0.00458 0.01408 0.7482
beta2 -0.00378 0.003017 0.2245
PQLの結果との乖離が大きい
41

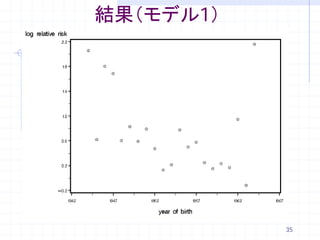
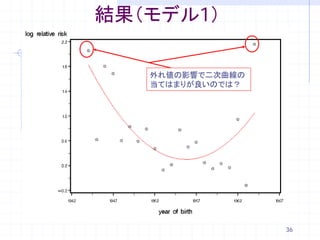
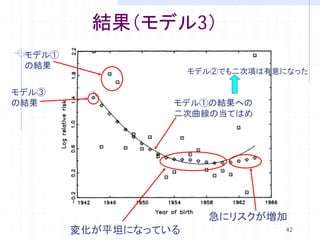
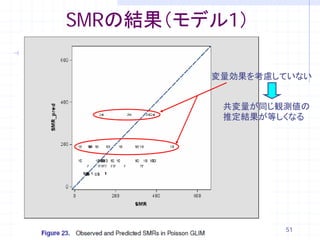
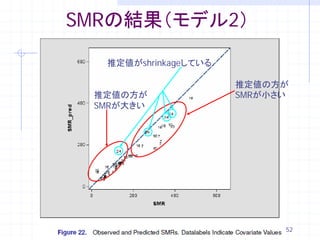
42. 結果（モデル3）
モデル①
の結果
モデル②でも二次項は有意になった
モデル③
の結果 モデル①の結果への
二次曲線の当てはめ
急にリスクが増加
変化が平坦になっている 42

43. 6.5 Spatial Aggregation in Scottish Lip
Cancer Rates
スコットランドで口腔癌の発症率を調査
 調査期間：1975~1980
 56郡で調査
 期待死亡数はClayton and Kaldor(1987)が報告
 SMRを観測値から計算
目的
 郡ごとの相対リスクを知りたい
 SMRを知りたい Clayton and Kalder(1987) Biometrics,43,671-81
43

44. データセット
data lipcancer;
input county observed expected employment SMR;
if (observed > 0) then expCount =
100*observed/SMR;
else expCount = expected;
datalines;
1 9 1.4 16 652.2 オフセット項の準備
2 39 8.7 16 450.3
3 11 3.0 10 361.8 職業：日に当たる時間の代替指標
4 9 2.5 24 355.7
・・・
44

45. モデル
1.固定効果のみのモデル
log µi= log ni + α 0 + α1 xi /10
b
2.郡の変量効果が独立であると仮定
log µi= log ni + α 0 + α1 xi /10 + bi , bi ~ N ( 0, σ 2 ) , i.i.d .
b
3.郡の変量効果に自己回帰構造を想定
log µi= log ni + α 0 + α1 xi /10 + bi
b
R ：Basag(1991)の構造を仮定
45

46. SASプログラム（モデル1）
proc glimmix data=lipcancer; 日照時間を示す変数
x = employment / 10; オフセット項
logn = log(expCount);
model observed = x / dist=poisson offset=logn solution
ddfm=none;
SMR_pred = 100*exp(_zgamma_ + _xbeta_);
固定効果の検定：
id employment SMR SMR_pred;
F検定，t検定→χ2検定，z検定
output out=glimmixout;
ポアソン分布を仮定
run;
データセットに出力する
変数の指定
46

47. SASプログラム（モデル2）
proc glimmix data=lipcancer;
class county;
x = employment / 10;
logn = log(expCount);
model observed = x / dist=poisson offset=logn solution
ddfm=none;
random county;
SMR_pred = 100*exp(_zgamma_ + _xbeta_);
id employment SMR SMR_pred; 変量効果を指定
output out=glimmixout;
run;
47

48. パラメータの結果（モデル1，2）
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept -0.5419 0.06951 Infty
モデル1
-7.80 <.0001
x 0.7374 0.05954 Infty 12.38
<.0001
Intercept -0.4406 0.1572 Infty -2.80
0.0051
x 0.6799 0.1409 Infty 4.82 <.0001
Cov Standard モデル2
固定効果パラメータ Parm Estimate Error
がattenuateしている county 0.3567 0.09869
48

49. パラメータの結果（モデル1~3）
固定効果を入れることで分散が減少
固定効果パラメータが
→日照時間は地域の影響を良く説明している
attenuateしている
固定効果をattenutateさせるような他の因子
（交絡要因）がないか考察するべき 49

50. GLIMMIXとGENMOD
GLMMでの周辺モデルとGLIMは同じ
proc glimmix data=lipcancer;
model observed = x / dist=poisson offset=logn solution;
run;
proc genmod data=lipcancer;
model observed = x / dist=poisson offset=logn
solution;
run;
50

51. SMRの結果（モデル1）
変量効果を考慮していない
共変量が同じ観測値の
推定結果が等しくなる
51

52. SMRの結果（モデル2）
推定値がshrinkageしている
推定値の方が
推定値の方が SMRが小さい
SMRが大きい
52

53. 7.Discussion and Conclutions
GLMの枠組みで変量効果を考慮することができた
階層が複雑でもGoldstein(1986)などの方法で解析可能
PQLの問題点
 変量効果パラメータが多いとコンピュータ計算が大変
 PQLでは分散行列が正定にならないこともある
 一次と二次の積率しか与えてないことによる情報不足
 固定効果パラメータが分散の推定値に大きく依存
→GibbsサンプリングやBootstrap法が良い場合もある
53

54. 7.Discussion and Conclutions
MQLについて
 シミュレーションでは固定効果パラメータがattenuationした
 固定効果パラメータについてはMQLとGEEは等しい
他の研究との関連
 MQLはGoldsteinのGLMMと等しい
 リンク関数が非線形の場合はPQLとNLMIXは等しい
 作業行列Yを使うことの正当化
自己回帰構造について
 Zeger(1988)やGoldstein(1991)がさらなる研究
 このようなモデルはベイズ流のアプローチと関係がある
54