第１回R勉強会＠東京 発表資料

1. R と統計学の基礎
id:yokkuns 里洋平
第 1 回 R 勉強会＠東京
1

2. 自己紹介
● id:yokkuns
●
名前 : 里 洋平
●
職業 :Web エンジニア
●
出身 : 種子島
●
趣味 : プログラミングとかカラオケとか
●
最近、何故か数学に興味がある
2

3. アジェンダ
●
R について
●
データ構造
●
データの入出力
●
データの視覚化
●
記述統計
●
推定
●
検定
3

4. R について
4

5. R とは
●
オープンソースでフリーソフトウェアの統計
解析向けプログラミング言語
●
S 言語のクローンとして開発されたが、 S-
PLUS よりも多くの場合高速
●
関数型・オブジェクト型
5

6. なぜ R を使うのか
●
オープンソースである事による信頼性
●
プログラミング言語であること
●
最近の統計解析手法への対応
6

7. R の導入
●
RjpWiki を見てください！
– R のインストール
http://www.okada.jp.org/RWiki/?R%20%A4
●
Fedora とかだと yum で入ります。
– yum install R
7

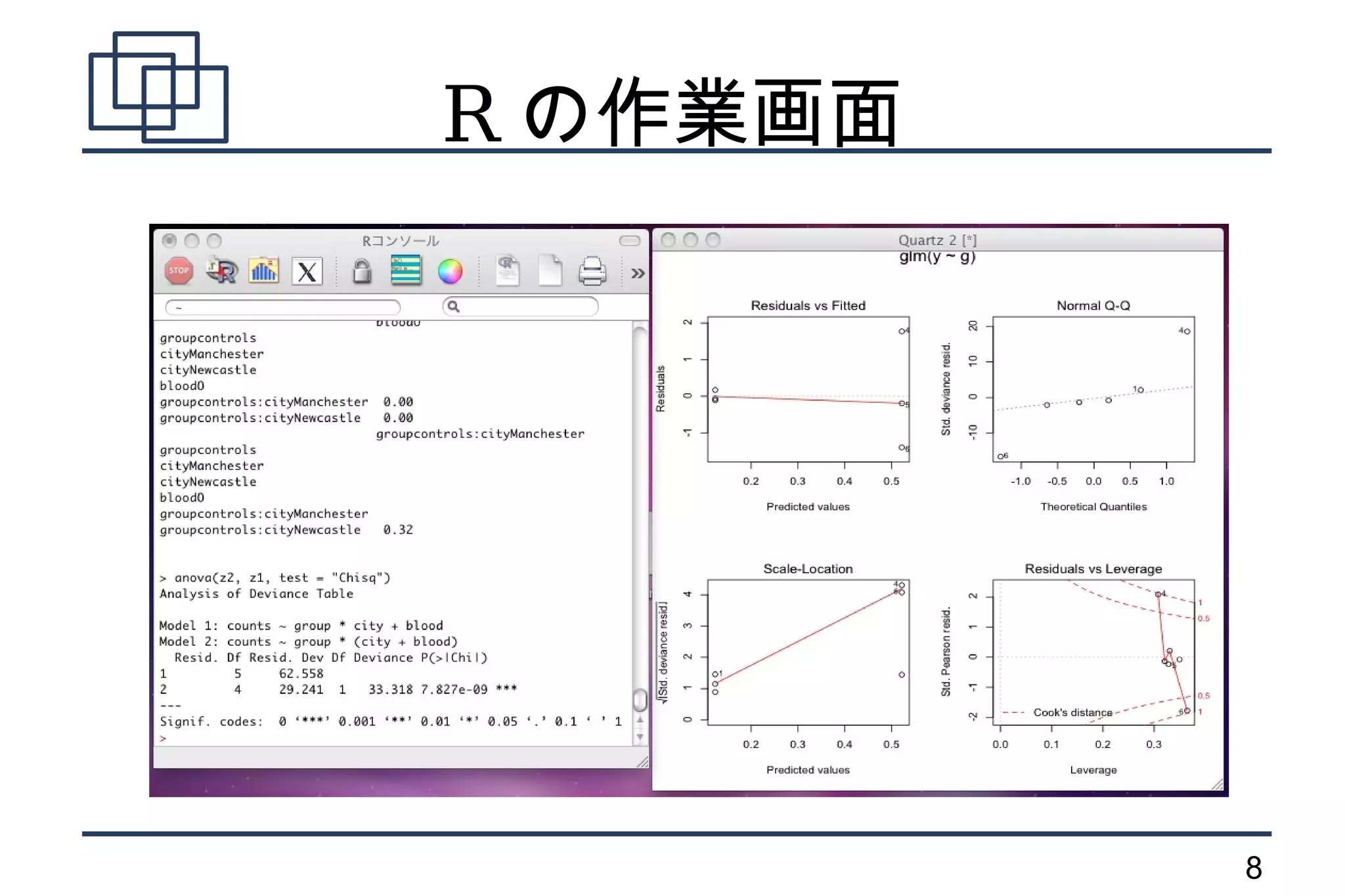
8. R の作業画面
8

9. R の作業画面
メニュー
コンソール グラフィックス画
面
9

10. R の作業画面（ ESS ）
10

11. R の基本操作
四則演算
べき算「 ^ 」
平方根「 sqrt 」
和「 sum 」
平均「 mean 」
代入「 <- 」
11

12. データ構造
12

13. データ構造
●
ベクトル
●
行列
●
リスト
●
データフレーム
13

14. ベクトル
●
データをある順序で並べたもの
– 数値ベクトル
– 論理ベクトル
– 文字ベクトル
●
同じデータ型でしか作れない
●
c() 関数で作成する
●
演算は、要素毎に行われる
14

15. 数値ベクトル
●
順序付けられた数値の集まり
●
n:m で 1 づつ増加（減少）する数列
●
seq() 関数で規則的な数列
– seq(from, to, by) : 増分を指定
– seq(from, to, length) : 長さを指定
15

16. 数値ベクトル（例）
※ ちなみに、名前付きパラメータは、順序は勝手で良い
16

17. 論理ベクトル
●
TRUE or FALSE の集まり
●
通常の算術演算で使うと、 0 と 1 に強制変換
される。
17

18. 文字列ベクトル
●
文字列の集まり。ダブルクォートで括られる
●
c() 関数で作成
●
paste() 関数で連結
18

19. ベクトルの要素の部分集合
●
ベクトルの要素の部分集合は、以下のような
添字ベクトルを使って表現出来る
– 論理ベクトル
– 正の整数値ベクトル
– 負の整数値ベクトル
– 文字列ベクトル
19

20. 添字ベクトル ( 論理 )
●
添字ベクトルは、要素を選び出すベクトルと
同じ長さを持つ必要あり
●
TRUE に対応する値が選択される。
20

21. 添字ベクトル ( 整数値 )
●
添字ベクトルは、任意の長さ
●
正の整数値 : 対応するベクトルが選択される
●
負の整数値 : 対応するベクトル以外が選択さ
れる
21

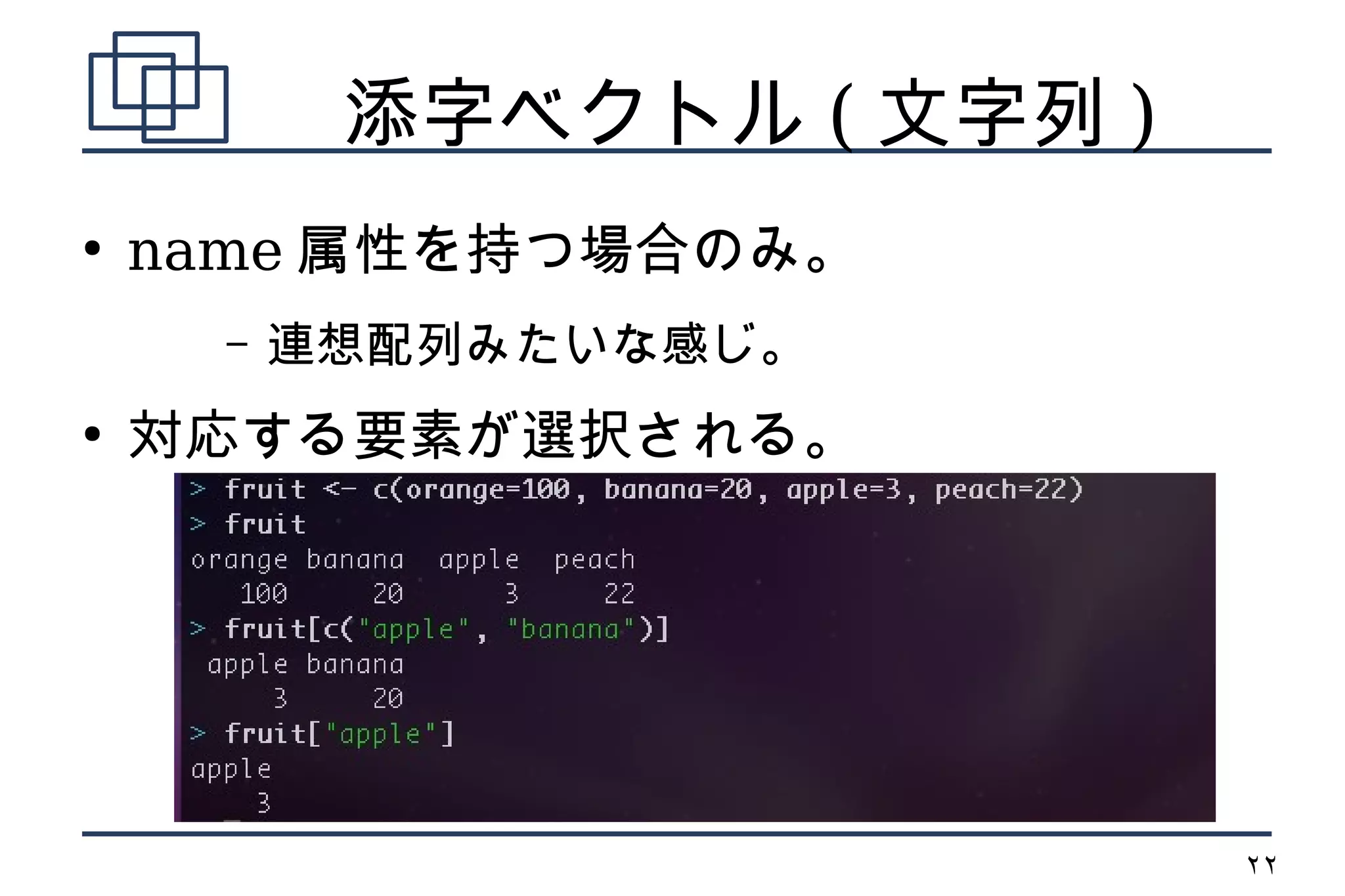
22. 添字ベクトル ( 文字列 )
●
name 属性を持つ場合のみ。
– 連想配列みたいな感じ。
●
対応する要素が選択される。
22

23. 行列
●
長さが同じである複数のベクトルを１つの
データセットとしてまとめた n 行 m 列の
データセット
●
同じデータ型
●
matrix() 関数、 cbind() 関数、 rbind() 関数
23

24. matrix()
●
要素ベクトルから行列を作る
●
matirx( 要素 , nrow= 行数 , ncol= 列数 )
●
24

25. rbind() 、 cbind()
●
複数のベクトルから行列を作る
– rbind( 行ベクトル 1, 行ベクトル 2, ...)
– cbind( 列ベクトル 1, 列ベクトル 2, ...)
25

26. リスト
●
順序付けられたオブジェクトの集まり
●
個々の成分は、コンポネントと呼ばれる
●
コンポネントは、同じ型である必要は無い
– 数値ベクトル、論理ベクトル、文字列、行
列、関数、その他 ...
●
list() 関数で作成
26

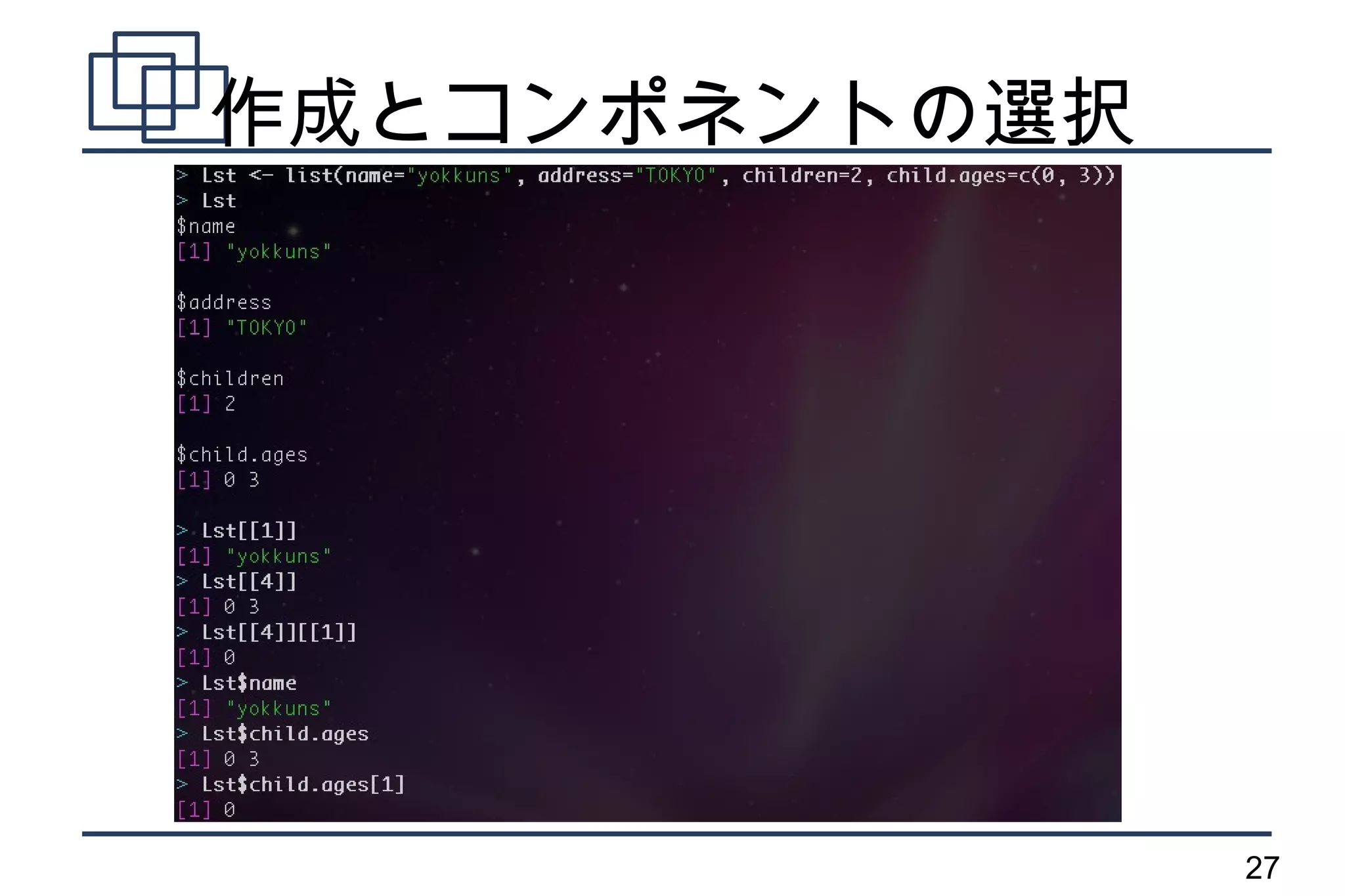
27. 作成とコンポネントの選択
27

28. 構造（余裕があったら）
28

29. 構造（余裕があったら）
余裕無かった
29

30. データフレーム
●
data.frame クラスを持つリスト
●
コンポネントは、ベクトルに限られる
●
行列、リスト、データフレームは、それぞれ
持つ列、要素、変数と同じ数の新しいデータ
フレームに付け加える
●
data.frame() 関数、 read.table() 関数
30

31. 作成
31

32. データの入出力
32

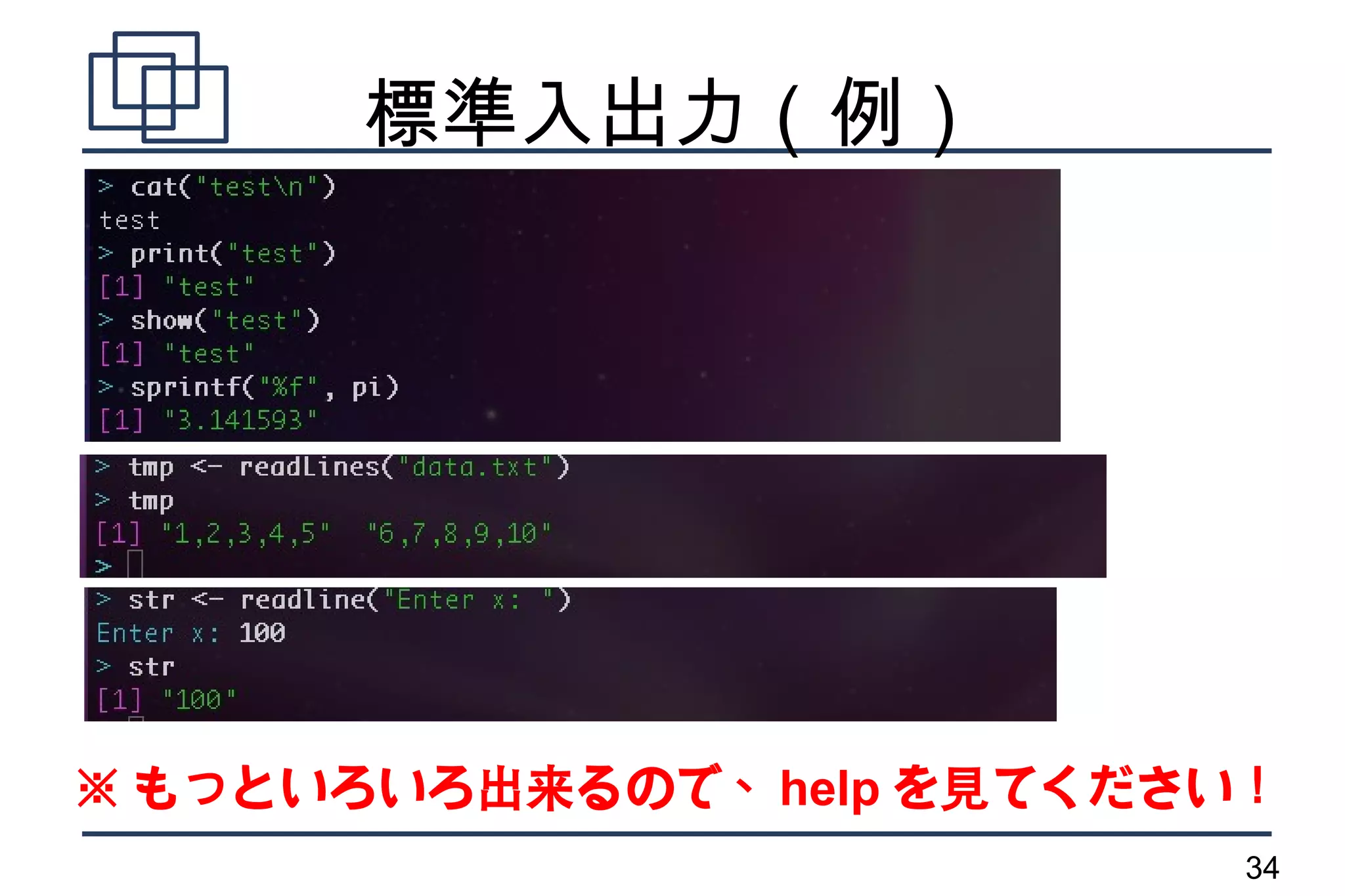
33. 標準入出力
●
標準出力
– cat()
– print()
– show
– sprintf
●
標準入力
– readLines
– readline
33

34. 標準入出力（例）
※ もっといろいろ出来るので、 help を見てください！
34

35. データの読み込み
●
scan() 関数
– コンソールやファイルからデータを読み込
み、ベクトルやリストにする
●
read.table() 関数
– 表形式のファイルを読み込みデータフレーム
にする
35

36. R コードの読み込み
●
source() 関数
– ファイル、 URL 、コネクションから R コー
ドを読み込む
36

37. データの視覚化
37

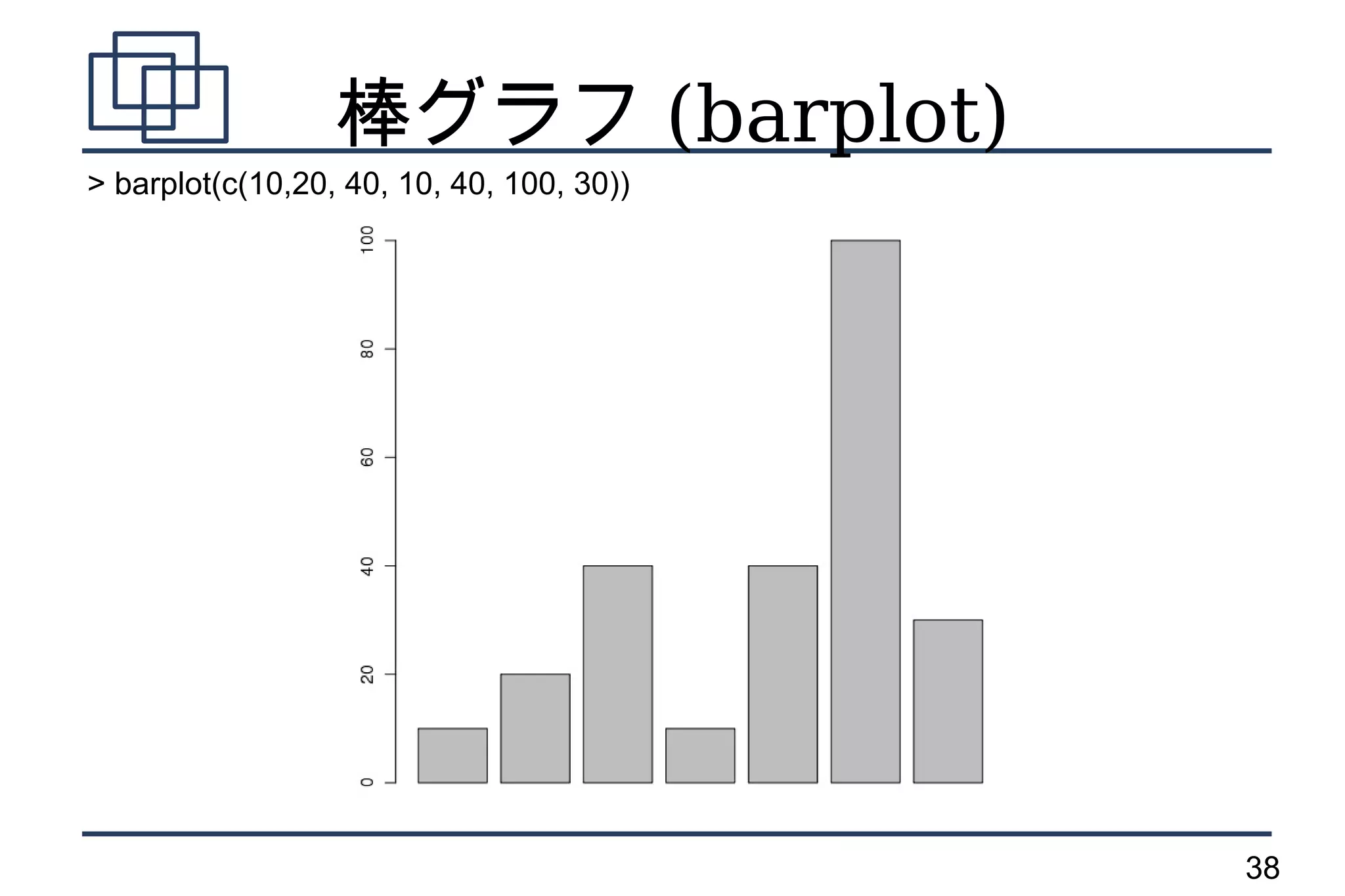
38. 棒グラフ (barplot)
> barplot(c(10,20, 40, 10, 40, 100, 30))
38

39. 円グラフ (pie)
> pie(c(10,20, 40, 30))
39

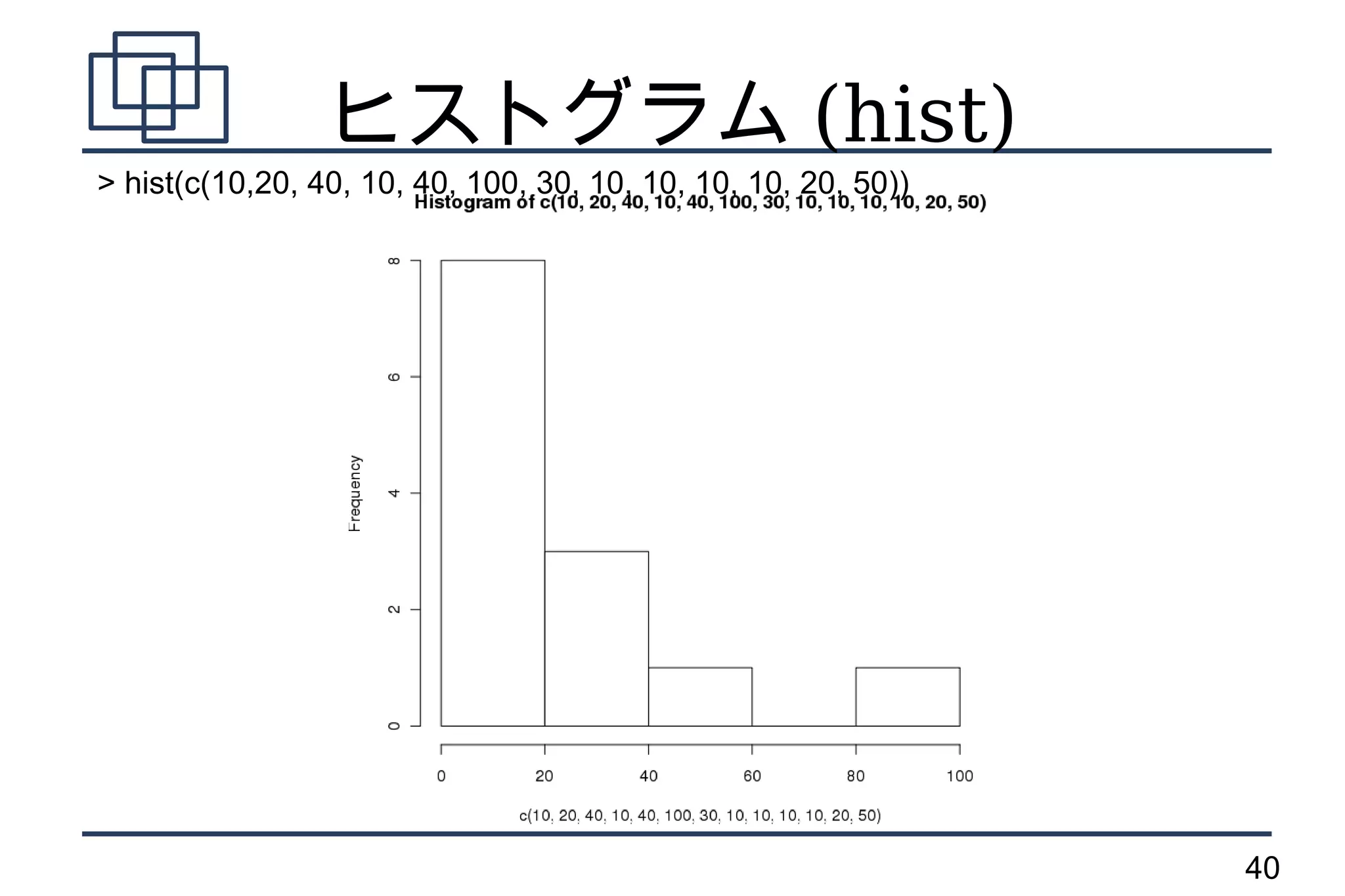
40. ヒストグラム (hist)
> hist(c(10,20, 40, 10, 40, 100, 30, 10, 10, 10, 10, 20, 50))
40

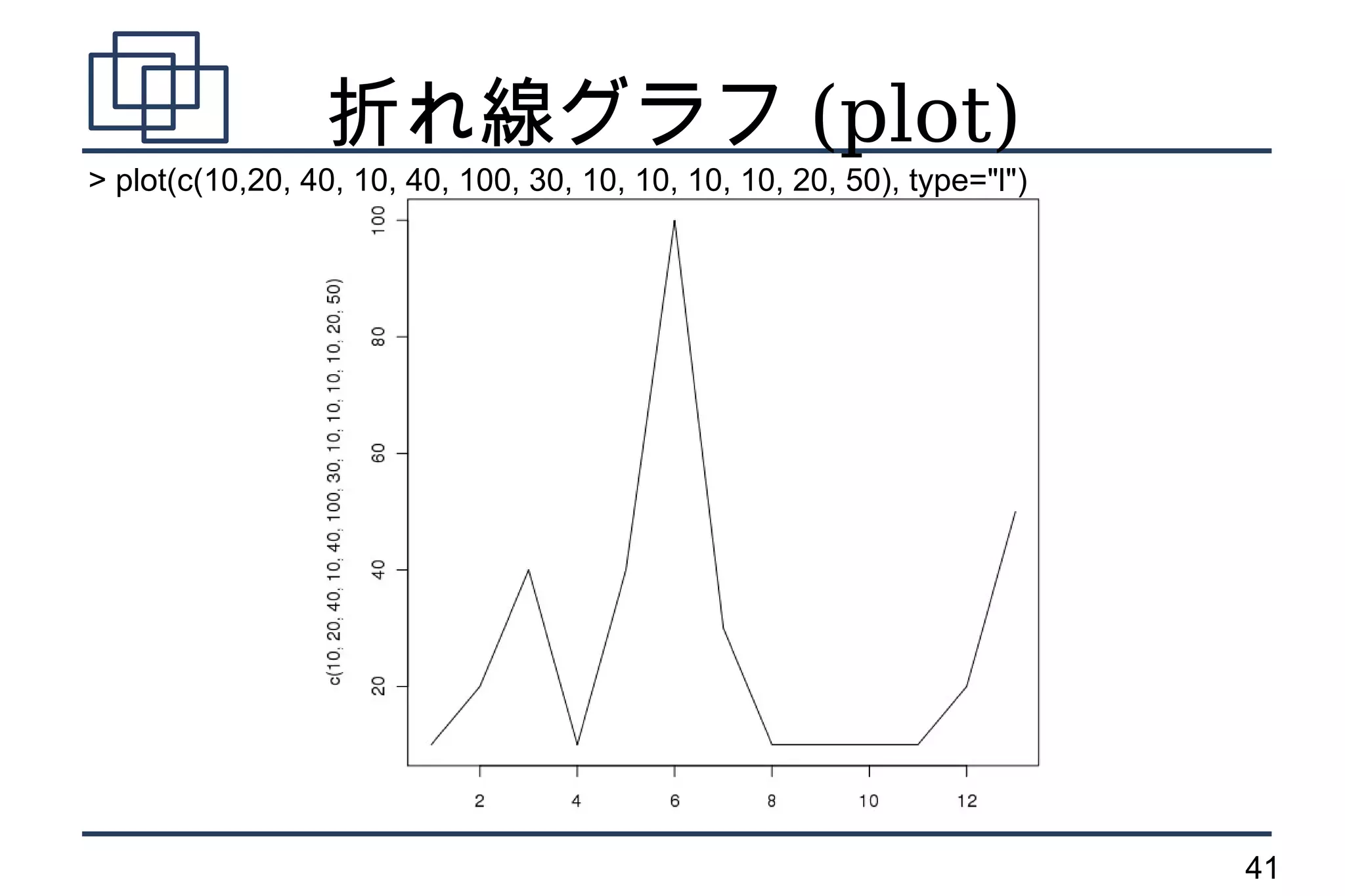
41. 折れ線グラフ (plot)
> plot(c(10,20, 40, 10, 40, 100, 30, 10, 10, 10, 10, 20, 50), type="l")
41

42. 箱ひげ図 (boxplot)
> boxplot(count ~ spray, data = InsectSprays)
42

43. 散布図 (plot)
> test1 <- c(6, 10, 6, 10, 5, 3, 5, 9, 3, 3, 11, 6, 11, 9, 7, 5, 8, 7, 7, 9)
> test2 <- c(10, 13, 8, 15, 8, 6, 9, 10, 7, 3, 18, 14, 18, 11, 12, 5, 7, 12, 7, 7)
> plot(test1, test2)
43

44. 散布図 (3 次元 )
> pairs(iris[1:4], main = "Anderson's Iris Data -- 3 species",
pch = 21, bg = c("red", "green3", "blue")[unclass(iris$Species)])
44

45. 統計学の基礎
45

46. 確率の復習
46

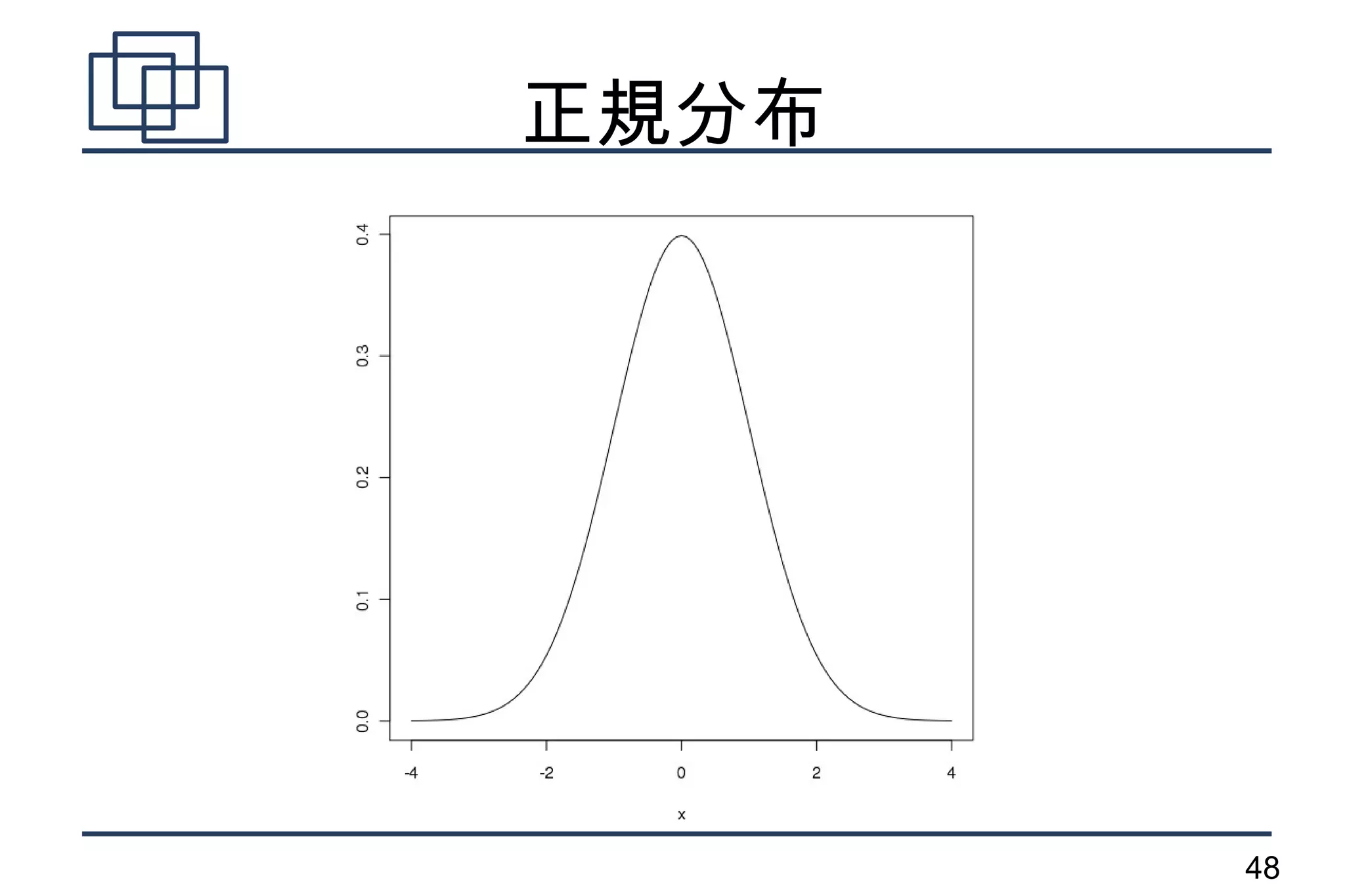
47. 確率変数と確率分布
●
確率変数
– 結果が得られるまで値が決まっていない変数。
●
実現値
– 実際に得られた値
●
確率分布
– ある確率変数がどのような値をどのような確率
で取るかを表した分布
47

48. 正規分布
48

49. カイ 2 乗分布
49

50. t 分布
50

51. 統計の分類
51

52. 記述統計と推測統計
●
記述統計
– 母集団そのものを扱う統計
●
推測統計
– 母集団から無作為に抽出した標本を扱う統計
52

53. 1 変数データの
記述統計
53

54. データの視覚的表現
●
度数 : 同じカテゴリに含まれるデータの個数
●
度数分布表 : 全カテゴリの度数をまとめた表
●
ヒストグラム : 度数分布表を棒グラフで表し
たもの
●
table() 関数
●
hist() 関数
54

55. データの視覚的表現
55

56. データの視覚的表現
56

57. 母集団を代表する数値
●
平均
– mean() 関数
●
中央値
– 大きさの順に並べた場合に中央に位置する値
– median() 関数
●
最頻値
– 最も頻繁に観測される値
– max(table(x)) で取得
57

58. 母分散と標準偏差
●
母集団のバラツキを表す指標
●
母分散
– v ← var(x) * (length(x) -1) / length(x)
●
標準偏差
– sqrt(v)
58

59. 標準化と偏差値
●
標準化
– 平均と標準偏差がある特定の値になるように
全てのデータを変換すること
– 平均 0 、標準偏差 1 がよく使われる
●
偏差値
– 平均 50 、標準偏差 10
59

60. 2 変数データの
記述統計
60

61. 相関
●
正の相関
– x が増加→ y が増加、 x が減少→ y が減少
●
負の相関
– x が増加→ y が減少、 x が減少→ y が増加
●
無相関
– x 、 y の変化に特に関係ない
61

62. 散布図
62

63. 共分散と相関係数
●
共分散
– 偏差の積の平均
– cov() 関数
●
相関係数
– 相関の強さ
– cor() 関数
63

64. 回帰直線
●
散布図で、ある程度相関があるとき、データ
をうまく表す１本の直線（ y = ax +b ）
●
lm() 関数
64

65. 回帰直線
65

66. 推測統計
66

67. 推測統計の分類
●
推定
– 点推定
– 区間推定
●
検定
66

68. 推定
68

69. 点推定と区間推定
●
点推定
– 母集団の母数の値を、抽出した標本から推定
●
区間推定
– 信頼区間にたいして母数の取り得る値の範囲
を求める
69

70. 推定量と推定値
●
推定量
– 母数を推定するために用いられる標本統計量
– 特に母数と等しい場合、不偏推定量という
●
推定値
– 標本データを用いて計算された推定量の値
70

71. 母数と推定量
●
母平均
– 標本平均 mean()
●
母分散
– 不偏分散 var()
●
母標準偏差
– 不偏標準偏差 sd()
●
母相関係数
– 標本相関係数 cor()
71

72. 区間推定
●
母集団の未知の母数 θ に対して
P(θ1 <= θ <= θ2) = 1 – α
– θ1 <= θ <= θ2 : 信頼区間
– α : 有意水準
●
具体的には、母集団の確率分布を正規分布と
仮定して母平均と母分散の区間推定を行う
72

73. 検定
73

74. 統計的仮説検定
●
母集団の母数についてある仮説をたて、それ
を棄却するかどうかを統計的に検定するこ
と。
●
考え方は区間推定に似ている。
74

75. 統計的仮説検定の手順
●
母集団に関する帰無仮説と対立仮説を設定
●
検定推定量を選ぶ
●
有意水準 α の値を決める
●
データから検定推定量の実現値を求める
●
棄却域に入れば帰無仮説を棄却、入らなけれ
ば帰無仮説を採択
75

76. 標準正規分布を用いた検定
●
母分散が既知
●
検定統計量
–
– 標準正規分布に
従う
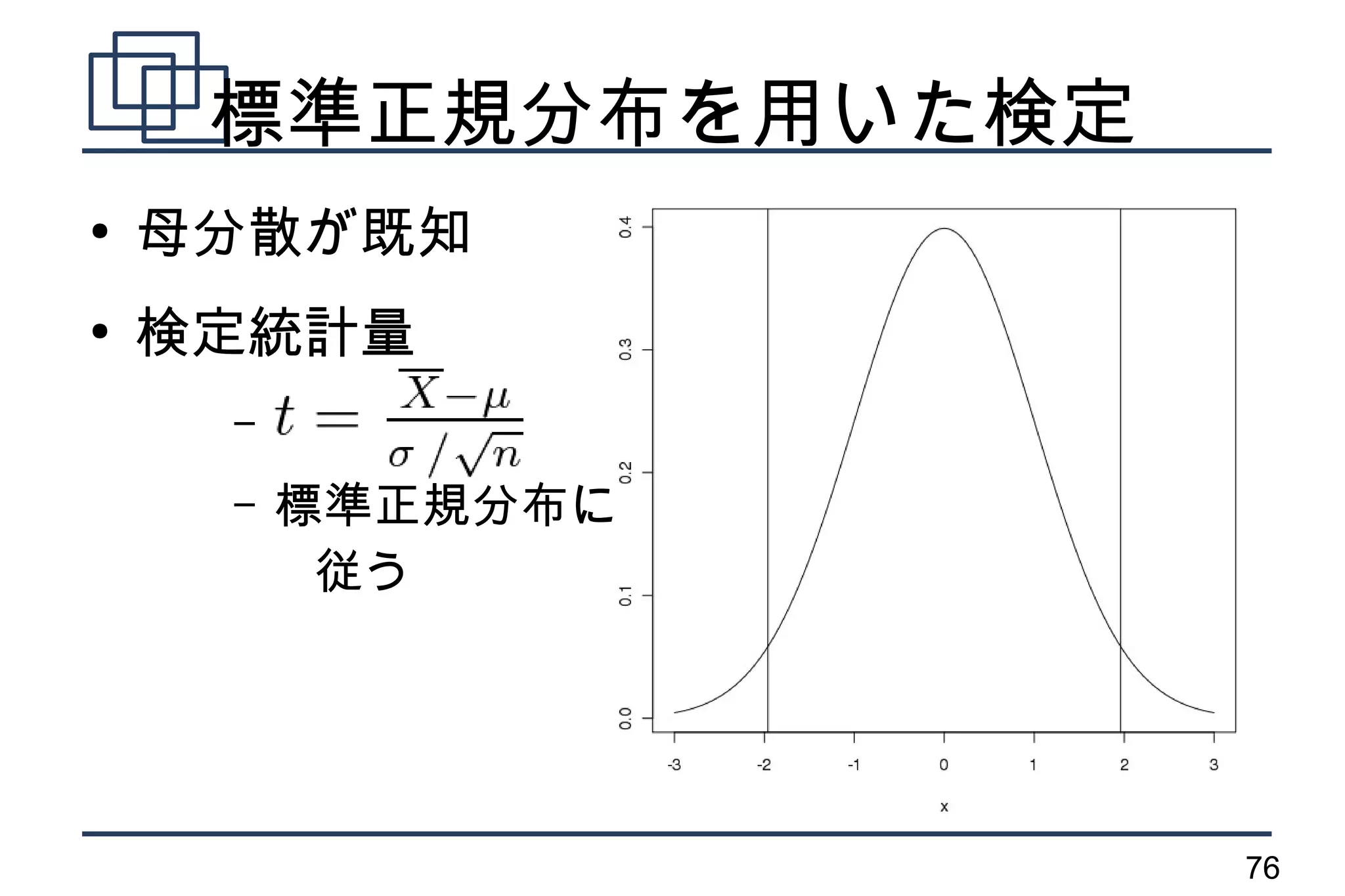
76

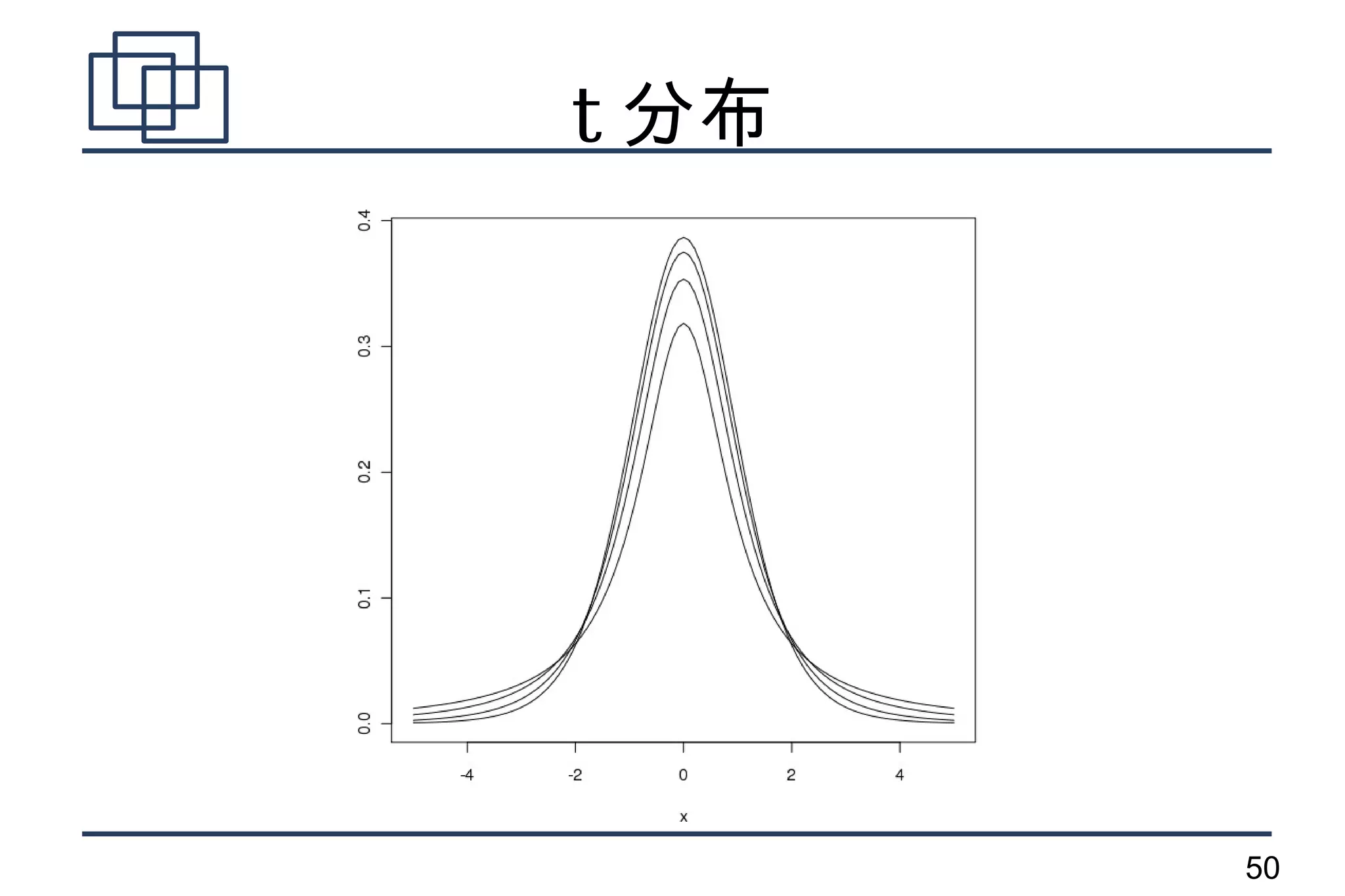
77. T 分布を用いた検定
●
母分散が未知
●
検定統計量
–
– 自由度 n-1 の
t 分布に従う
●
t.test() 関数
77

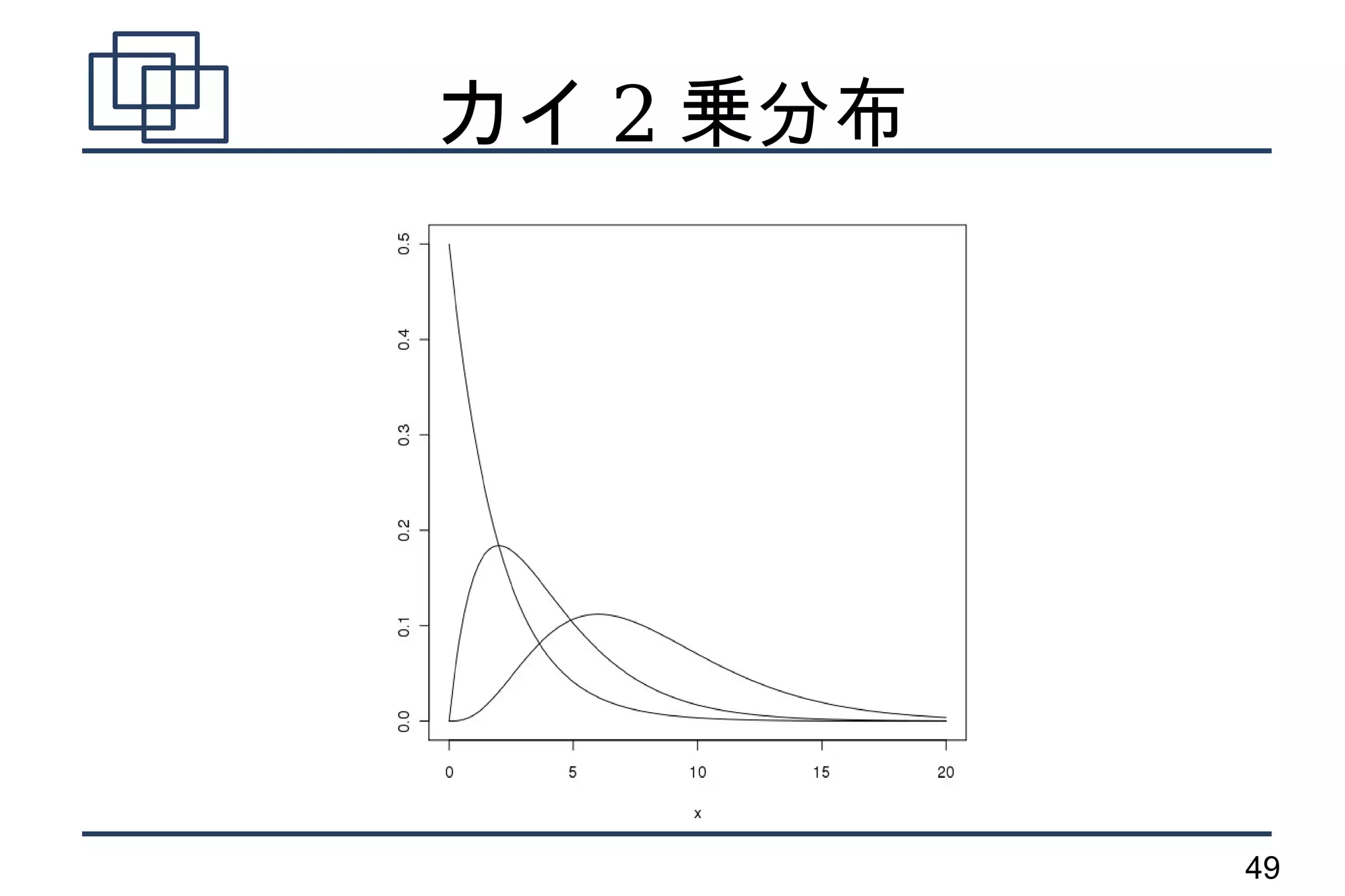
78. カイ二乗検定
●
独立性の検定
●
検定統計量
– 自由度 1 のカイ
二乗分布に従う
●
chisq.test() 関数
78

79. ご清聴ありがとうございました。
79

80. 参考文献
●
Rによるやさしい統計学
●
確率統計キャンパスゼミ
●
Rプログラミングマニュアル
80