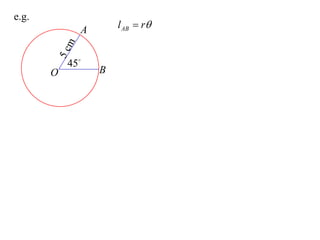
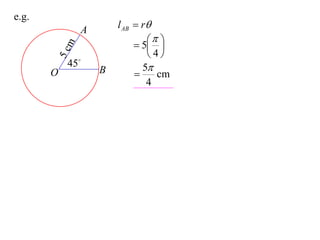
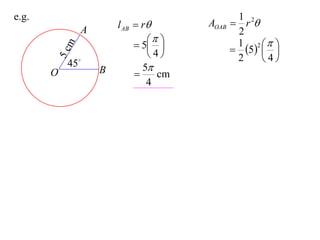
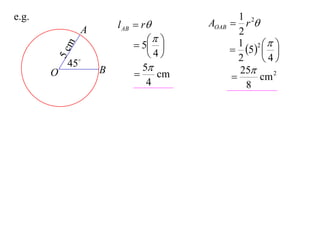
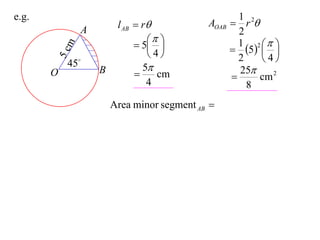
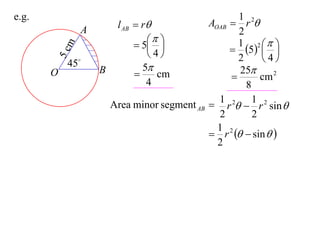
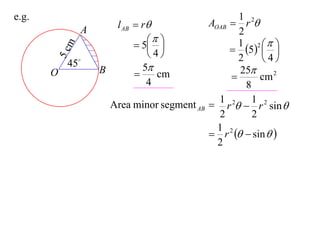
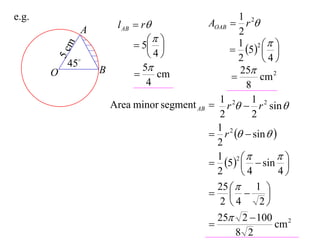
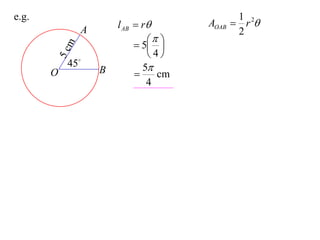
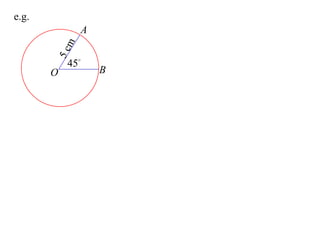
The document discusses trigonometric functions, arcs, sectors, and related concepts. It defines: - 360° = 2π radians - The circumference of a circle is given by C = 2πr - The area of a circle is given by A = πr^2 - The length of an arc is given by l = rθ - The area of a sector is given by A = (1/2)r^2θ It provides an example calculating the length of an arc and area of a sector for a circle with radius 5cm and central angle of 45°.

1. Trigonometric Functions

2. Trigonometric Functions
360  2 radians

3. Trigonometric Functions
360  2 radians
Arcs & Sectors

4. Trigonometric Functions
360  2 radians
Arcs & Sectors
C  2r

5. Trigonometric Functions
360  2 radians
Arcs & Sectors
C  2r A  r 2

6. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
O 
B

7. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
O 
B
AB is an arc

8. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
O  l
B
AB is an arc

9. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2

l  2r
O  l 2
B
AB is an arc

10. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2

l  2r
O  l 2
l  r
B
AB is an arc

11. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2

l  2r
O  l 2
l  r
B
Length of an arc; l  r
AB is an arc

12. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2

l  2r
O  l 2
l  r
B
OAB is a sector
Length of an arc; l  r
AB is an arc

13. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
 
l  2r AOAB   r 2
O  l 2 2
l  r
B
OAB is a sector
Length of an arc; l  r
AB is an arc

14. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
 
l  2r AOAB   r 2
O  l 2 2
l  r 1
B AOAB  r 2
2
OAB is a sector
Length of an arc; l  r
AB is an arc

15. Trigonometric Functions
360  2 radians
Arcs & Sectors
A C  2r A  r 2
 
l  2r AOAB   r 2
O  l 2 2
l  r 1
B AOAB  r 2
2
OAB is a sector
Length of an arc; l  r
AB is an arc 1 2
Area of a sector; A  r 
2

16. e.g.
A
m
5c 45
O B

17. e.g.
A l AB  r
m
5c 45
O B

18. e.g.
A l AB  r
 
 5 
m
4
5c 45
O B

19. e.g.
A l AB  r
 
 5 
m
4
5c 45
B 5
O  cm
4

20. e.g. 1
l AB  r AOAB  r 2
A 2
 
 5 
m
4
5c 45
B 5
O  cm
4

21. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5
O  cm
4

22. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5 25
O  cm  cm 2
4 8

23. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5 25
O  cm  cm 2
4 8
Area minor segment AB 

24. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5 25
O  cm  cm 2
4 8
1 1
Area minor segment AB  r 2  r 2 sin 
2 2
1 2
 r   sin  
2

25. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5 25
O  cm  cm 2
4 8
1 1
Area minor segment AB  r 2  r 2 sin 
2 2
1 2
 r   sin  
2

26. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c 45
2 4
B 5 25
O  cm  cm 2
4 8
1 1
Area minor segment AB  r 2  r 2 sin 
2 2
1 2
 r   sin  
2
1 2 
 5   sin 
2 4 4
25   1 
   
2 4 2
25 2  100 2
 cm
8 2

27. e.g. 1
l AB  r AOAB  r 2
A 2
  1 2 
 5   5  
m
4  
5c45
2 4
B 5 25
O  cm  cm 2
4 8
1 1
Area minor segment AB  r 2  r 2 sin 
2 2
1 2
 r   sin  
2
1 2 
 5   sin 
Exercise 14B; 2 to 24 evens, 25, 28* 2 4 4
25   1 
   
2 4 2
25 2  100 2
 cm
8 2