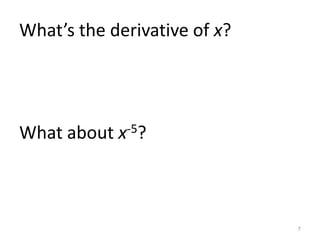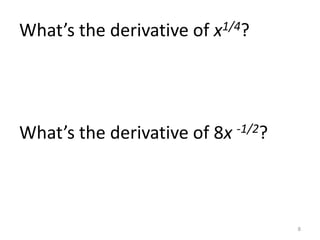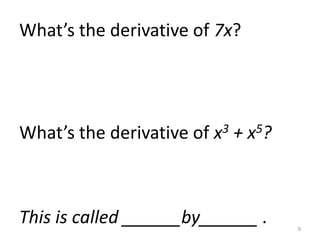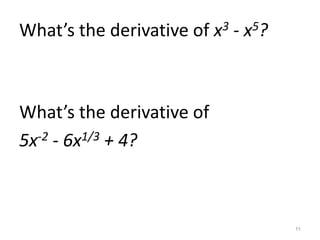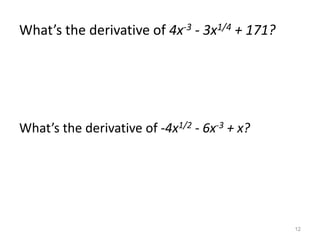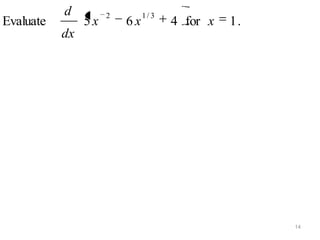This document provides an overview of differentiation formulas and concepts, including: 1) The derivative of a constant is 0. The Power Rule states that when taking the derivative of f(x)=x^n, the power is brought down and the exponent is decreased by 1. 2) Evaluation of a derivative involves taking the derivative of a function and plugging in a value. The derivative f'(x) gives the slope of the tangent line to the function f(x) at that point. 3) Leibniz notation represents the derivative of a function f(x) with respect to x as df/dx. Derivatives are used in business and economics to find marginal cost, revenue

1. 1

2. 7.4 Some Differentiation Formulas
A. Derivative of a Constant
B. Power Rule
C. Evaluation of a Derivative
D. Leibniz Notation
E. Derivatives in Business and Economics
2

3. A. Derivative of a Constant
• The derivative of a constant is _______.
• Examples:
3

4. B. Power Rule
• The power comes down front with the
coefficient, and you deduct one from the power.
Here’s the rule:
n
If f x x , then the derivative ,
d n 1
f x or f x n x
dx
4

5. 5

6. Power Rule
• The power comes down front with the
coefficient, and you deduct one from the
power. Here are examples:
6

7. What’s the derivative of x?
What about x-5?
7

8. What’s the derivative of x1/4?
What’s the derivative of 8x -1/2?
8

9. What’s the derivative of 7x?
What’s the derivative of x3 + x5?
This is called ______by______ . 9

10. In order to find derivatives term by
term, they must actually be terms.
What are terms?
10

11. What’s the derivative of x3 - x5?
What’s the derivative of
5x-2 - 6x1/3 + 4?
11

12. What’s the derivative of 4x-3 - 3x1/4 + 171?
What’s the derivative of -4x1/2 - 6x-3 + x?
12

13. C. Evaluation of a Derivative
13

14. d 2 1/ 3
Evaluate 5x 6x 4 for x 1.
dx
14

15. 4
If f x x , then find f 2 .
15

16. 4
If f x 3x 2x, then find the slope of the
line that is tangent t o the curve at x 3.
16

17. The power rule can NOT be used
on this as it is written right now.
Why not?
2
2x 3x 1
f x
x
17

18. Remember when your algebra teacher taught
you this:
• Rewrite this so that it has no denominators:
2
2x 3x 1
f x
x
18

19. The reason we need to that is …
• We are not able to use the power rule on
2
2x 3x 1
f x
x
• But we know to differentiate this:
• So rewriting it will be your very first step!
19

20. You try differentiating:
3 2
6x 3x 2x 1
f x 2
x
20

21. DON’T FORGET WHAT A DERIVATIVE IS
• It’s a function for the slope of the tangent line.
• If you plug in a value for x. Let’s say, you find
the derivative of f and call it f prime. Then
suppose you plug in x = 3 into f prime and get
4. So that f’(3) = 4. What does this mean?
• THE LINE THAT IS TANGENT TO f AT THE POINT
x=3 HAS A SLOPE OF 4.
21

22. D. Leibniz Notation
df
Instead of writing f 2 , Leibniz wrote
dx x 2
3 df
If f x 4 x , find
dx x 1
22

23. E. Derivatives in Business & Economics
• COST FUNCTIONS:
• C(x) is a function for
“total cost of producing x units.”
• MC(x) is for “MARGINAL COST” and it is the
same as C’(x), the derivative of C(x).
• Marginal Cost gives you COST PER UNIT.
23

24. REVENUE FUNCTIONS:
• R(x) is a function for the total revenue from
selling x units.
• MR(x) is for “MARGINAL REVENUE,” and it is
the same as R’(x), the derivative of R(x).
• Marginal Revenue gives you REVENUE PER
UNIT.
24

25. PROFIT FUNCTIONS:
• P(x) is a function for the total profit from
producing and selling x units.
• Profit = Revenue minus Cost
• P(x) = R(x) – C(x)
• MP(x) = P’(x) = Marginal Profit = Profit
per item
25

26. A company manufactur es cordless telephone s and finds
its cost function (the total cost of making x telepho nes) is
C ( x) 400 x 500 dollars. Find MC(x).
Find the marginal cost when 100 telephone s have been
made, and interpret your answer.
26

27. A researcher finds that the # of names that a person can
3 2
memorize in x minutes is f x 6 x . Find the IRC of
this function after 8 minutes and interpret your answer.
(How does that differ in meaning from f(8)?)
27

28. You try : A company sells rocking chairs and finds its
2
revenue function is R ( x ) 23 x dollars. Find MR(x).
Find the marginal revenue when 20 rocking chairs have
been sold, and interpret your answer.
(But how is that different from what R(20) means?)
28