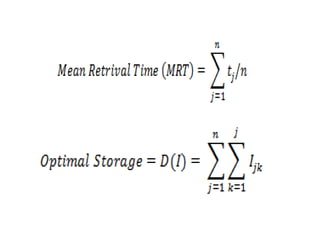
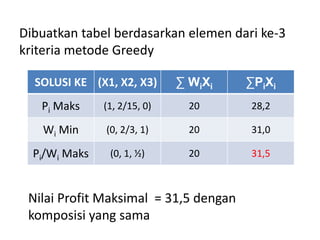
Dokumen tersebut membahas metode greedy dalam penyelesaian masalah optimasi. Metode ini mengambil keputusan lokal yang optimal pada setiap langkah untuk mencapai solusi global yang optimal. Beberapa contoh masalah yang dapat diselesaikan dengan metode ini adalah optimal storage, knapsack problem, minimum spanning tree, dan shortest path problem.

1. Metode Greedy
Dyah Darma Andayani

2. Pendahuluan
• Metode Greedy digunakan untuk memecahkan
persoalan optimasi.
• Persoalan optimasi  adalah persoalan mencari
solusi optimum
• Persoalan optimasi ada 2 Maksimasi
 Minimasi
• Untuk mendapatkan solusi optimal dari
permasalahan yang mempunyai dua kriteria yaitu
Fungsi Tujuan/utama dan nilai pembatas
(constraint)

3. Contoh Masalah Optimasi
• Penukaran Uang
• Diberikan uang senilai A. Tukar A dengan koin-koin
uang yang ada.
• Berapakah jumlah minimum koin yang diperlukan
untuk penukaran uang tersebut.
• Jumlah minimum koin → Persoalan Minimasi.
• Contoh 1: tersedia banyak koin 1, 5, 10, 25
32 = 1 + 1 + … + 1 (32 koin)
32 = 5 + 5 + 5 + 5 + 10 + 1 + 1 (7 koin)
32 = 10 + 10 + 10 + 1 + 1 (5 koin)
Minimum: 32 = 25 + 5 + 1 + 1 (4 koin)

4. • Greedy = rakus, tamak
• Algoritma greedy membentuk solusi langkah per
langkah (step by step).
• Pada setiap langkah terdapat banyak pilihan yang
perlu dieksplorasi.
• Sehingga, pada setiap langkah harus dibuat
keputusan yang terbaik dalam menentukan
pilihan.
• (keputusan yang telah diambil pada suatu
langkah tidak dapat diubah lagi pada langkah
selanjutnya).
• Pada setiap langkah  membuat pilihan
optimum lokal
• Dengan harapan bahwa langkah sisanya
mengarah kesolusi optimum global.

5. Proses Kerja Metode Greedy
• Untuk menyelesaikan suatu permasalahan
dengan n input data yang terdiri dari beberapa
fungsi pembatas dan satu fungsi tujuan yang
diselesaikan dengan memilih beberapa solusi
yang mungkin (feasible solution/feasible
sets), yaitu bila telah memenuhi fungsi
tujuan/obyektif.

6. Metode Greedy digunakan untuk dalam
penyelesaian masalah :
• Optimal Storage on Tapes Problem
• Knapsack Problem
• Minimum Spanning Tree Problem
• Shortest Path Problem

7. 1. Optimal Storages On Tapes Problem
• Permasalahan : Bagaimana mengoptimalisasikan
storage/memory dalam komputer agar data yang
tersimpan dalam komputer dapat termuat dengan
optimal.
• Misalkan terdapat n program yang akan disimpan
didalam pita (tape). Pita tersebut mempunyai
panjang maksimal sebesar L, masing-masing
program yang akan disimpan mempunyai panjang
L1, L2, L3,...Ln. Cara penyimpanan adalah
penyimpanan secara terurut (sekuensial).

8. • Persoalan : Bagaimana susunan penyimpanan
program-program tersebut sehingga :
L1 + L2 + L3 + ....+ Ln = L ?
• Pemecahannya : Jika program-program
tersebut disimpan dalam orde, dimisalkan
adalah orde 1, yaitu : j sama dengan ∑tik maka
akan didapat k=1.

10. • Contoh :
Misal terdapat 3 buah program (n=3) yang
masing-masing mempunyai panjang program
(I1, I2, I3) = (5,10,3). Tentukan urutan
penyimpanannya secara berurutan
(sekuensial) secara optimal.

11. • Penyelesaian :
Dari 3 buah program tersebut akan diperoleh
6 buah kemungkinan order, yang diperoleh
dari cara memfaktorialkan 3 = 3! .
ORDERING D (I)
1,2,3 5 + (5 +10) + (5 + 10 + 3) = 38
1,3,2 5 + (5 + 3) + (5 + 3+ 10) = 31
2,1,3 10 + (10 + 5)+(10 + 5 + 3) = 43
2,3,1 10 + (10 + 3) + (10 + 3 + 5) = 41
3,1,2 3 + (3 + 5) + (3 + 5 + 10) = 29
3,2,1 3 + (3 + 10) + (3 + 10 + 5) = 34

12. • Dari tabel tersebut dapat diperoleh bahwa
susunan order yang optimal adalah sebagai
berikut :
 Susunan pertama untuk program ketiga
 Susunan kedua untuk program kesatu
 Susunan ketiga untuk program kedua

13. 2. Knapsack Problem
• Knapsack dapat diartikan sebagai
karung, kantung, atau buntilan.
• Karung digunakan untuk memuat sesuatu.
• Dan tentunya tidak semua objek dapat
ditampung di dalam karung. Karung tersebut
hanya dapat menyimpan beberapa objek dengan
total ukurannya (weight) lebih kecil atau sama
dengan ukuran kapasitas karung.
• Setiap objek itupun tidak harus kita masukkan
seluruhnya. Tetapi bisa juga sebagian saja.

14. • knapsack 0/1, yaitu suatu objek diambil seluruh
bagiannya atau tidak sama sekali.
• Setiap objek mempunyai nilai keuntungan
atau yang disebut dengan profit.
• Tujuan ingin mendapatkan profit yang
maksimal. Untuk mendapatkan profit maksimal
Belum tentu menggunakan banyak objek
yang masuk akan menguntungkan. Bisa saja hal
yang sebaliknya yang terjadi.
– Cara terbaik agar menguntungkan : bukan hanya dari
hasilnya optimal tetapi juga banyaknya langkah yang
dibutuhkan

15. • Kasus : Terdapat n obyek ( Xi; i = 1,2,3,...,n) yang
masing-masing mempunyai berat (weight) Wi dan
masing-masing memiliki nilai profit Pi yang berbeda.
• Masalah : Bagaimana obyek-obyek tersebut
dimuat/dimasukkan dalam ransel (knapsack) yang
mempunyai kapasitas maksimum = M. Sehingga timbul
permasalahan sebagai berikut
• Bagaimana memilih obyek yang akan dimuat dari n
obyek yang ada sehingga nilai obyek termuat
jumlahnya sesuai dengan kapasitas ( M).
• Jika semua obyek harus termuat dalam ransel maka
berapa bagian dari setiap obyek yang ada dapat
dimuat ke dalam ransel sedemikian sehingga nilai
kum.maksimal dan sesuai dengan kapasitas ransel.

16. • Penyelesaian Knapsack Problem :
1. Secara Matematika
2. Dengan kriteria Greedy
3. Dengan algoritma pemrograman Greedy

17. 1. Penyelesaian Masalah Knapsack secara
Matematika
Fungsi Tujuan = fungsi utama/ objektif =
fungsi yang menjadi penyelesaian masalah
dengan mendapatkan solusi yang optimal.
Solusi yang dimaksud = menemukan
nilai/profit yang maksimum untuk jumlah
obyek yang dimuat dalam ransel sehingga
sesuai dengan kapasitas.
Fungsi Tujuan :

18. • Fungsi Pembatas = fungsi subyektif = fungsi
yang bertujuan untuk memberikan batas maks
dari setiap obyek untuk dapat dimuat dalam
ransel sehingga kapasitasnya tidak melebihi
dari jumlah maksimum daya tampung ransel.
Dimana : 0 Xi 1 ; Pi > 0 ; Wi > 0
Catatan : Karena menggunakan matematika sangat
sulit dan kompleks, maka tidak akan dibahas lebih
lanjut.

19. 2. Penyelesaian dengan Kriteria Greedy
Konsep dari kriteria yang ditawarkan oleh
metode Greedy, yaitu :
 Pilih obyek (barang) dengan nilai Pi
maksimal atau terbesar.
 Pilih obyek (barang) dengan berat Wi
minimal dahulu.
 Pilih obyek (barang) dengan perbandingan
nilai dan berat yaitu Pi/Wi yang terbesar.

20. • Contoh :
Diketahui bahwa kapasitas M = 20 kg.
Dengan jumlah barang n = 3
 Berat Wi masing-masing barang
(W1, W2, W3) = (18,15,10)
 Nilai Pi masing-masing barang
(P1, P2, P3) = (25, 24, 15)

21. Pilih barang dengan Nilai Profit Maksimal :
 P1 = 25 → X1 = 1 , dimisalkan sebagai batas
atas nilai
 P2 = 24 → X2 = 2/15 , dihitung dengan fungsi
pembatas.
 P3 = 15 → X3 = 0, dimisalkan sebagai batas
bawah nilai

22. Pilih barang dengan Berat Minimal :
 W1 = 18 → X1 = 0 sebagai batas bawah
 W2 = 15 → X2 = 2/3, dihitung dengan fungsi
pembatas.
 W3 = 10 → X3 = 1, sebagai batas atas

23. Pilih barang dengan menghitung perbandingan
yang terbesar dari Profit dibagi Berat (Pi/Wi)
yang diurut secara tidak naik, yaitu :
 P1/W1 = 25/18 → karena terkecil maka X1 = 0
 P2/W2 = 24/15 → karena terbesar maka X2 = 1
 P3/W3 = 15/10 → dengan fungsi pembatas
X3 = 1/2

24. Dibuatkan tabel berdasarkan elemen dari ke-3
kriteria metode Greedy
SOLUSI KE (X1, X2, X3) ∑ WiXi ∑PiXi
Pi Maks (1, 2/15, 0) 20 28,2
Wi Min (0, 2/3, 1) 20 31,0
Pi/Wi Maks (0, 1, ½) 20 31,5
Nilai Profit Maksimal = 31,5 dengan
komposisi yang sama