Downloaded 37 times
12 apt
- 1.
- 2. 2 BackgroundBackground • Estimating expectedreturn with the AssetEstimating expected return with the Asset Pricing Models of Modern FinancePricing Models of Modern Finance – CAPMCAPM • Strong assumption - strong predictionStrong assumption - strong prediction
- 3. Expected Return Risk (Return Variability) Market Indexon Efficient Set Market Index A B C Market Beta Expected Return Corresponding Security Market Line xxx xxxx xxxx xx xx x x x xxx xx x
- 4. Market Index Expected Return Risk (Return Variability) Market IndexInside Efficient Set Corresponding Security Market Cloud Expected Return Market Beta
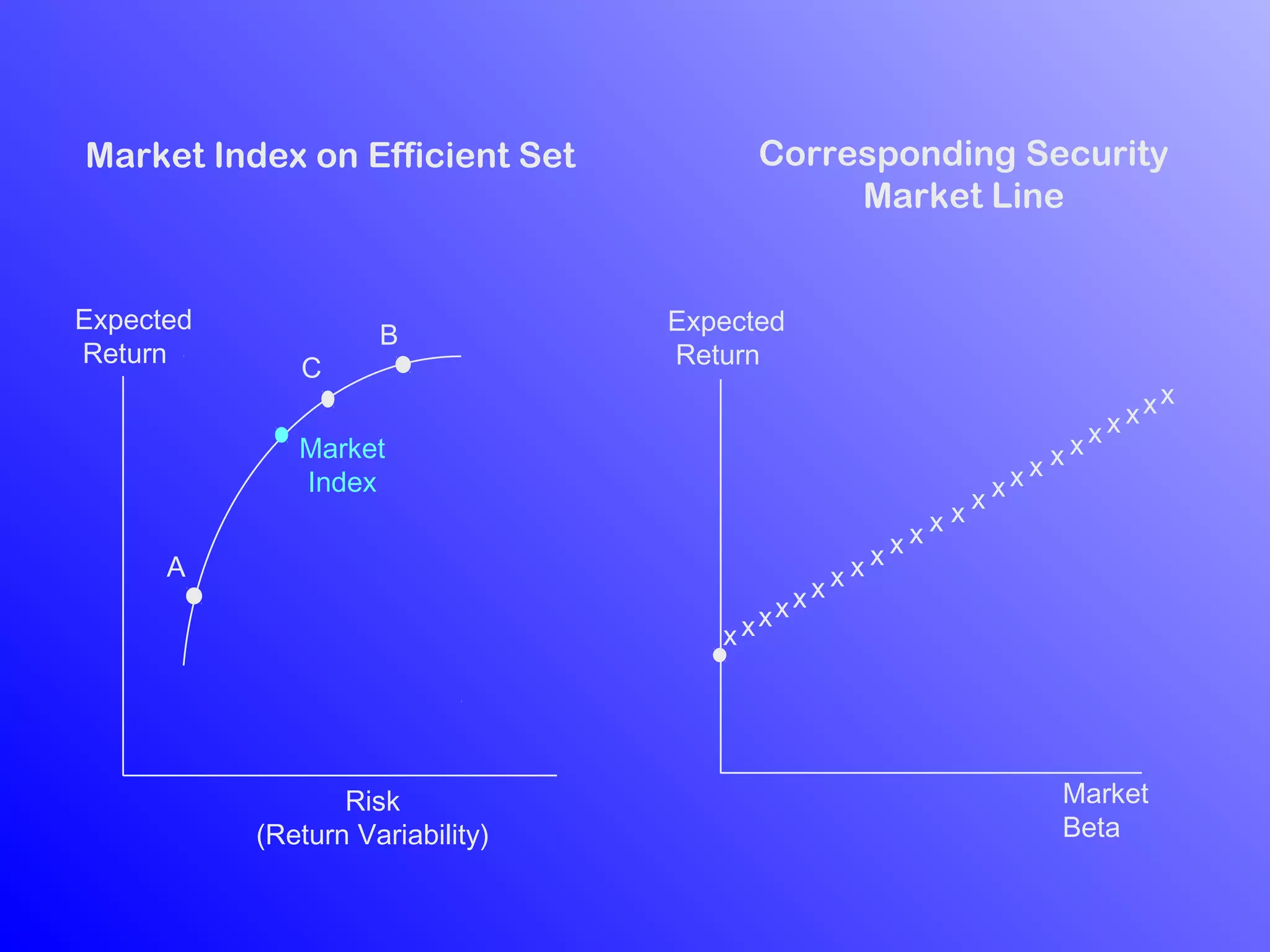
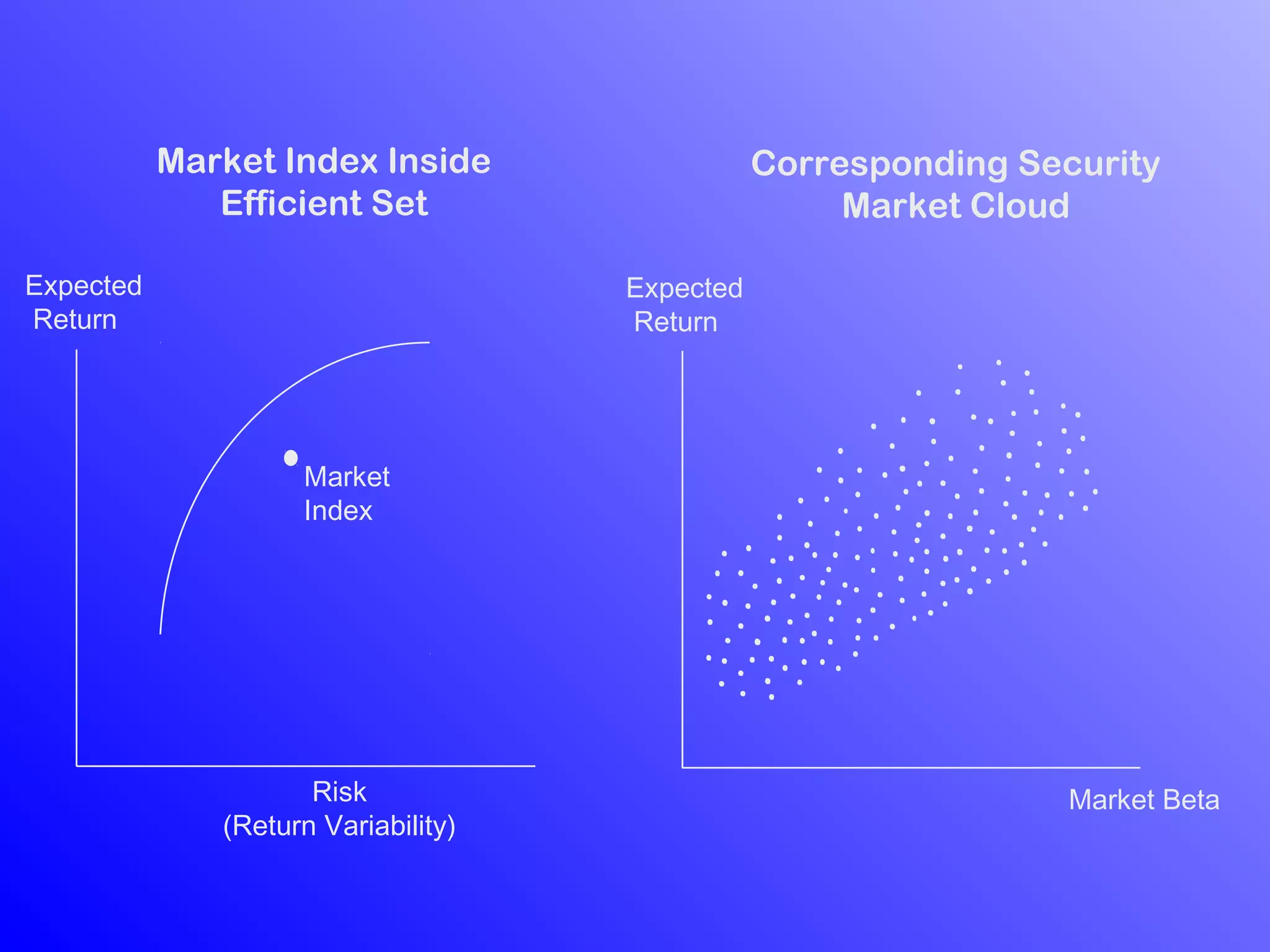
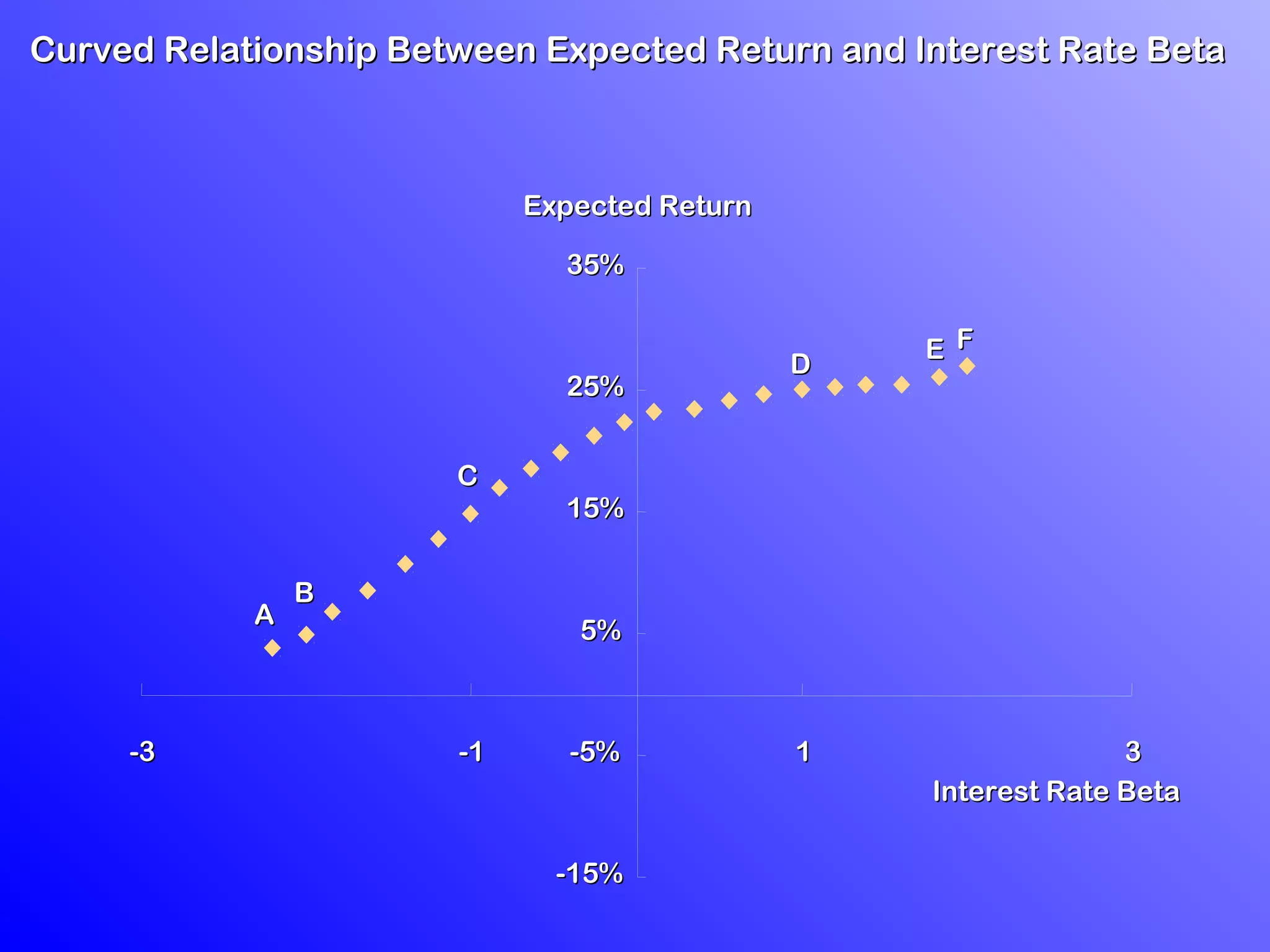
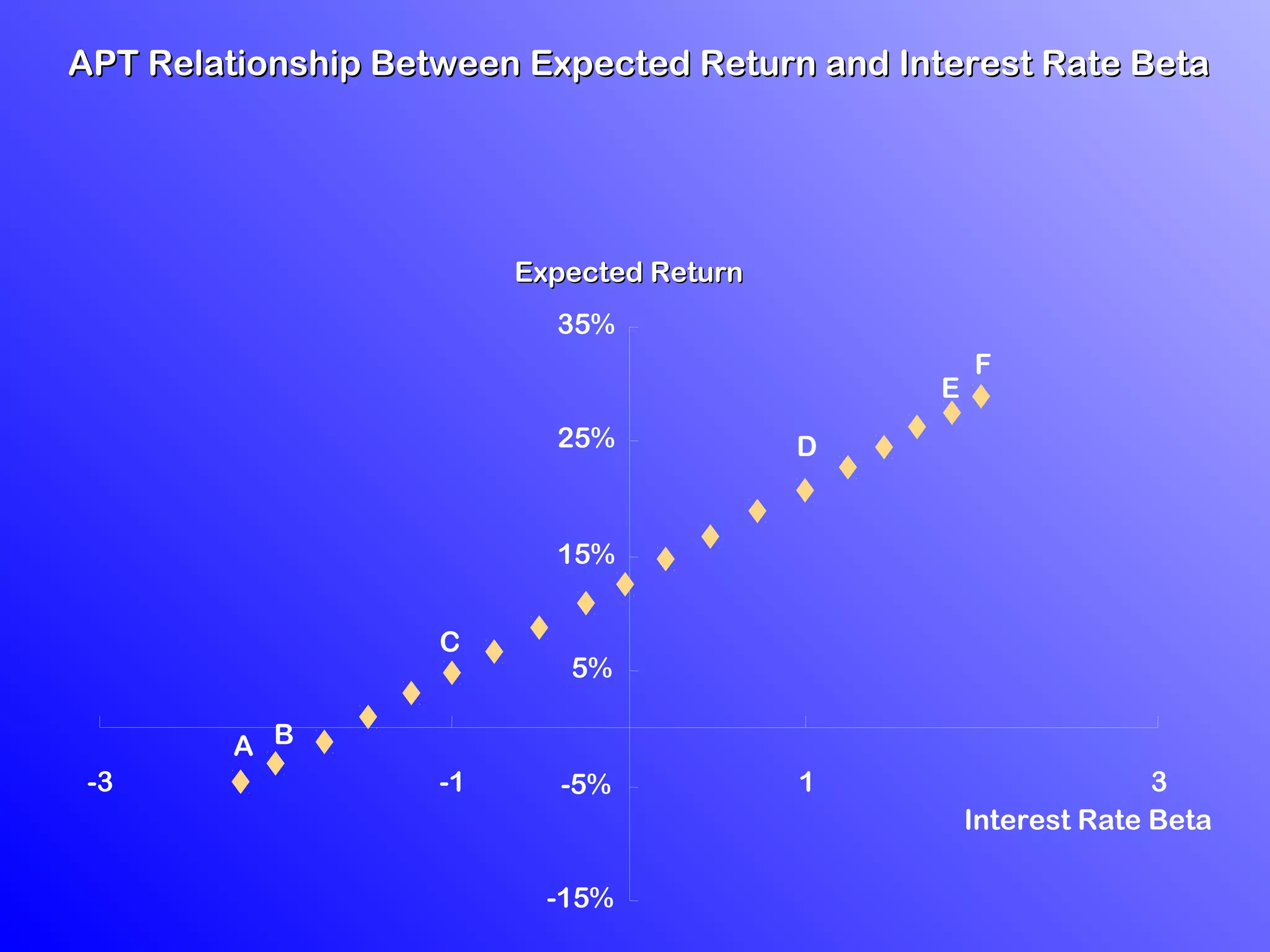
- 5. 5 FACTOR MODELS • ARBITRAGEPRICING THEORY (APT) – is an equilibrium factor model of security returns – Principle of Arbitrage • the earning of riskless profit by taking advantage of differentiated pricing for the same physical asset or security – Arbitrage Portfolio • requires no additional investor funds • no factor sensitivity • has positive expected returns – Example …
- 6. Curved Relationship BetweenExpected Return and Interest Rate BetaCurved Relationship Between Expected Return and Interest Rate Beta -15%-15% -5%-5% 5%5% 15%15% 25%25% 35%35% Expected ReturnExpected Return -3-3 -1-1 11 33 Interest Rate BetaInterest Rate Beta AA BB CC DD EE FF
- 7. • Two stocks A:E(r) = 4%; Interest-rate beta = -2.20 B: E(r) = 26%; Interest-rate beta = 1.83 Invest 54.54% in E and 45.46% in A Portfolio E(r) = .5454 * 26% + .4546 * 4% = 16% Portfolio beta = .5454 * 1.83 + .4546 * -2.20 = 0 With many combinations like this, you can create a risk-free portfolio with a 16% expected return. The Arbitrage Pricing TheoryThe Arbitrage Pricing Theory
- 8. The Arbitrage PricingTheoryThe Arbitrage Pricing Theory • Two different stocks C: E(r) = 15%; Interest-rate beta = -1.00 D: E(r) = 25%; Interest-rate beta = 1.00 Invest 50.00% in E and 50.00% in A Portfolio E(r) = .5000 * 25% + .4546 * 15% = 20% Portfolio beta = .5000 * 1.00 + .5000 * -1.00 = 0 With many combinations like this, you can create a risk-free portfolio with a 20% expected return. Then sell-short the 16% and invest the proceeds in the 20% to arbitrage.
- 9. 9 • No-arbitrage conditionfor asset pricing If risk-return relationship is non-linear, you can arbitrage. Attempts to arbitrage will force linearity in relationship between risk and return. The Arbitrage Pricing TheoryThe Arbitrage Pricing Theory
- 10. APT Relationship BetweenExpected Return and Interest Rate BetaAPT Relationship Between Expected Return and Interest Rate Beta -15% -5% 5% 15% 25% 35% Expected ReturnExpected Return -3 -1 1 3 Interest Rate Beta A B C D E F
- 11. 11 FACTOR MODELS • ARBITRAGEPRICING THEORY (APT) – Three Major Assumptions: • capital markets are perfectly competitive • investors always prefer more to less wealth • price-generating process is a K factor model
- 12. 12 FACTOR MODELS • MULTIPLE-FACTORMODELS – FORMULA ri = ai + bi1 F1 + bi2 F2 +. . . + biKF K+ ei where r is the return on security i b is the coefficient of the factor F is the factor
- 13. 13 FACTOR MODELS • SECURITYPRICING FORMULA: ri = λ0 + λ1 b1 + λ2 b2 +. . .+ λKbK where ri = rRF +(δ1−rRF )bi1 + (δ2− rRF)bi2+ . . . +(δ−rRF)biK
- 14. 14 FACTOR MODELS where ris the return on security i λ0 is the risk free rate b is the factor e is the error term
- 15. 15 FACTOR MODELS • hence –a stock’s expected return is equal to the risk free rate plus k risk premiums based on the stock’s sensitivities to the k factors