1. เรื่องแคลคูลัสเบื้องต้น 1
โดยครูปอปลา คนส้วยสวย
คำ า แนะนำ า สำ า หรั บ ผู ้ เ รี ย น
١. แบบฝึกทักษะที่ ١.٢ ลิมิตและความต่อเนื่องของฟังก์ชัน (2) นี้มีผล
การเรียนรู้
ที่คาดหวัง คืือ พิจารณาหาลิมิตของฟังก์ชันจากฟังก์ชันได้ ใช้เวลา ٢
ชั่วโมง
٢. ให้ผู้เรียนทำาแบบฝึกทักษะลงในชุดที่ครูแจกให้หรือทำาลงในสมุดของ
นักเรียนก็ได้
และหากทำาไม่ทันตามเวลาที่กำาหนดไว้ในแบบฝึกทักษะให้นำาไปทำา
ต่อเป็นการบ้าน
แล้วนำามาส่งครูในวันรุ่งขึ้นได้
٣. ผูเรียนจะต้องศึกษาแบบฝึกทักษะเรียงตามลำาดับขันตอน โดยเริมจาก
้ ้ ่
การฟังครูอธิบาย
นิยาม ทฤษฎี ตัวอย่าง และซักถามจากครูให้เข้าใจก่อนแล้วจึงเข้า
กลุ่มและลงมือ
ทำาแบบฝึกทักษะหากไม่เข้าใจหรือสงสัยในขณะที่กำาลังทำาแบบฝึก
ทักษะให้ผู้เรียน
สอบถามเพิ่มเติมจากครูหรือจะซักถามจากเพื่อนในกลุ่มที่เรียนดีก็ได้
แล้วมาทำาต่อ
ด้วยตนเอง อย่าให้มีการลอกแบบฝึกทักษะกันส่ง
٤. หลังจากทำาแบบฝึกทักษะเสร็จแล้วให้ส่งครูเพื่อตรวจ หากได้คะแนน
เกิน ٧٥% ของ
คะแนนเต็มในแต่ละแบบฝึกทักษะถือว่าผ่านเกณฑ์ ก็ให้ผู้เรียนทำาแบบ
ทดสอบท้าย
แบบฝึกทักษะนั้น ๆ เพื่อตรวจสอบความเข้าใจอีกครั้งหนึ่ง แต่ถ้าหาก
ไม่ผ่านเกณฑ์
ก็ให้ผู้เรียนย้อนกลับไปศึกษาทบทวนและทำาการแก้ไขแบบฝึกทักษะ
ข้อที่ผดอีกครั้ง
ิ
จนผ่านแล้วจึงให้ทำาแบบทดสอบท้ายแบบฝึกทักษะเพื่อตรวจสอบ
ความเข้าใจ
5. หากผู้เรียนทำาแบบทดสอบท้ายแบบฝึกทักษะถูกไม่ถึง ٧٥%ของ
จำานวนข้อสอบ
ให้ทำาการซ่อมเสริมด้วยการซักถามข้อที่ไม่แน่ใจจากครู แล้วให้ลอง
ทำาแบบทดสอบ
เดิมอีกครั้ง จนผ่าน จึงจะไปศึกษาแบบฝึกทักษะชุดต่อไปได้
(คะแนนเก็บของแบบฝึกทักษะชุดนี้ คือ ٥ คะแนน)

2. เรื่องแคลคูลัสเบื้องต้น 2
โดยครูปอปลา คนส้วยสวย
١.2 ลิ ม ิ ต และความต่ อ เนื ่ อ งของฟั ง ก์ ช ั น (2)
การพิจารณาหาลิมิตของฟังก์ชัน จากฟังก์ชัน
ทฤษฎีบท
เมื่อ a , L และ M เป็นจำำนวนจริงใด ๆ ถ้ำ f และ g เป็นฟังก์ชันที่มี
โดเมน
และเรนจ์เป็นสับเซตของเซตของจำำนวนจริง โดยที่ x→af(x) = L
lim และ
lim g(x) = M แล้ว
x→ a
1. x→ac = c เมื่อ c เป็นค่ำคงตัวใด ๆ
lim
2. lim x = a
x→ a
+
3. x→ax = a , n∈ I
lim n n
4. lim c f(x) = c lim f(x) = cL, c เป็นค่ำคงตัวใด ๆ
x→ a x→ a
5. [ + ]
limf(x) g(x)= limf(x) limg(x) L + M
x→ a
+
x→ a
=
x→ a
6. x→a[ f(x) − g(x)] = x→af(x) − x→ag(x) = L − M
lim lim lim
7. x→a[ f(x) ⋅ g(x)] = x→af(x) ⋅ x→ag(x) = L ⋅ M
lim lim lim
 f(x)  x→af(x) L
lim
8. x→a g(x)  = limg(x) = M, M ≠ 0
lim
  x→a
9. [ ] n
[ ] n
limf(x) = limf(x) = Ln, n∈ I+
x→a x→a

3. เรื่องแคลคูลัสเบื้องต้น 3
โดยครูปอปลา คนส้วยสวย
10. x→a f(x)= n x→ a f(x) L, n∈ I − {1 และ
}
+
limn lim = n n
L∈R
ตั ว อย่ า ถ้ำ f(x) = x2 – 3 จงหำ x→2 f(x)
lim
วิธีทำา limf(x) = limx2 − lim3 (ทฤษฎีบท 6)
x→2 x→2 x→2
= 22 − 3 = 1 (ทฤษฎีบท 1 , 3)
ตั ว อย่ า ถ้ำ f(x) = (x+2)2 จงหำ x→5 f(x) lim
วิธีทำา เนื่องจำก x→5(x + 2) = x→5 x + x→52 (ทฤษฎีบท 5)
lim lim lim
= 5+ 2
=7 (ทฤษฎีบท 1-2)
ดังนั้น lim + 2) = [ lim + 2) 2
(x 2 (x ] (ทฤษฎีบท 9)
x→ 5 x→ 5
= 72
= 49
ตั ว อย่ า ถ้ำ f(x) = 2x − 2x จงหำ x→5 f(x)
lim
3 3
เนื่องจำก x→5(2x − 2x) = 2(5 ) − 2(5)
lim 3 3
วิธีทำา (ทฤษฎีบท 2-4, 6)
= 250− 1 0= 240
ดังนั้น limf(x) = 3 lim(2x3 − 2x) (ทฤษฎีบท 10)
x→5 x→5
= 240= 23 30
3

4. เรื่องแคลคูลัสเบื้องต้น 4
โดยครูปอปลา คนส้วยสวย
ตั ว อย่ า ถ้ำ f(x) = (x + 1 )(3x − 2) จงหำ lim f(x)
2
x→−1
วิธีทำา เนื่องจำก xlim1 (x + 1 ) = (−1 ) + 1 = 2
2 2
→−
(ทฤษฎีบท 1, 3)
และ lim(3x 2) 3( 1)− 2 = − 5 (ทฤษฎีบท 1, 2)
− = −
x→ −1
ดังนั้น =
limf(x)
x→ −1
[ x→ −1
2
lim(x + 1) ][ −
lim(3x 2)
x→ −1
] (ทฤษฎีบท 7)
= (2)(−5)
= −1 0
x2 − x − 6
ตั ว อย่ า ถ้ำ f(x) = 2 จงหำ x→3 f(x)
lim
x + 2x − 1 5
วิธีทำา เนื่องจำก lim(x2 − x − 6) = 32 − 3− 6 = 0 (ทฤษฎีบท 1-3)
x→3
และ x→3(x + 2x − 1 5) = 3 + 2(3) − 1 5 = 0 (ทฤษฎีบท 1-4)
lim 2 2
0
limf(x) =
x→3 0
อำจจะหำค่ำได้หรืออำจจะหำค่ำไม่ได้จึงต้องเปลี่ยนรูป
แบบฟังก์ชันใหม่
โดยอำศัยควำมรูทำงพีชคณิตในกำรดึงตัวร่วมแยก
้

5. เรื่องแคลคูลัสเบื้องต้น 5
โดยครูปอปลา คนส้วยสวย
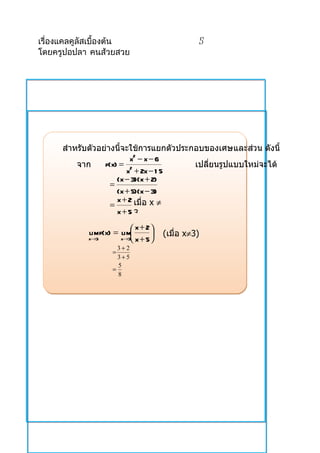
สำำหรับตัวอย่ำงนี้จะใช้กำรแยกตัวประกอบของเศษและส่วน ดังนี้
x2 − x − 6
จำก f(x) = 2 เปลียนรูปแบบใหม่จะได้
่
x + 2x − 1 5
(x − 3)(x + 2)
=
(x + 5)(x − 3)
x + 2 เมื่อ x ≠
=
x+5 3
x + 2
lim f(x) = lim
  (เมื่อ x≠3)
x→3 x→3 x + 5 
3+ 2
=
3+5
5
=
8

6. เรื่องแคลคูลัสเบื้องต้น 6
โดยครูปอปลา คนส้วยสวย
ตั ว อย่ า x2 − 1
ถ้ำ f(x) = จงหำ x→1 f(x)
lim
x−1
x2 − 1 (x − 1 )(x + 1 )
วิธีทำา จำก f(x) = = = x + 1 เมื่อ x≠1
x−1 x−1
lim f(x) = lim(x + 1 ) ข้อนี้ ทำำนองเดียวกับตัวอย่ำง
x→1 x→1
ที่ ٥
=1 + 1 ต้องเปลี่ยนรูปแบบฟังก์ชันใหม่
=2 โดย
x+ 2 − 2
ตั ว อย่ า ถ้ำ f(x) = จงหำ x→0 f(x)
lim
x
x+ 2 − 2 x+ 2 + 2
วิธีทำา จำก f(x) = ×
x x+ 2 + 2
( x + 2) − 2
=
x( x + 2 + 2
x ข้อนี้ ทำำนองเดียวกับตัวอย่ำง
=
x( x + 2 + 2 ที่ ٥ กล่ำวคือ ต้อง
1 เปลี่ยนรูปแบบของฟังก์ชันใหม่
= แต่ข้อนีใช้กำรแยกตัวประกอบ
้
x+2+ 2
ไม่ได้
limf(x) = lim
1  จึงต้องใช้กำรนำำสังยุคของเศษ
x→0
 
x→0 x + 2 + 2 
∴ 1
=
2 2

7. ชื่อ................................................................ชั้น..........
่
....เลขที.............
เรื่องแคลคูลัสเบื้องต้น 7
โดยครูปอปลา คนส้วยสวย
แบบฝึกทักษะที่ 1.2
ให้นักเรียนหำค่ำลิมิตของฟังก์ชันต่อไปนี้
1. x→4(−8)
lim = ………………………….
2. lim(4x)
x→3 = ………………………….
lim 2
3. x→2(3x ) = ………………………….
4. lim (−3x5 ) = ………………………….
x→−2
5. x→5(x + 2) = x→5(x) + x→5(2) = ………………………….
lim lim lim
6. lim(5 − 4x) = lim5− lim(4x) = ………………………….
x→7 x→7 x→7
7. lim (x + 9x) = ………………………….
2
x→−1
8. x→2(3x − 5) = ………………………….
lim 4
9. lim (2x3 − 5x + 8) = ………………………….
x→−1
10. xlim(x + 3x + x − 6) = ………………………….
4 2
→0
11. ถ้ำ f(x) = x + 22 จงหำ x→5 f(x)
lim
3
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
x−1
12. ถ้ำ f(x) = 2 จงหำ x→1 f(x)
lim
x −1
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….

8. เรื่องแคลคูลัสเบื้องต้น 8
โดยครูปอปลา คนส้วยสวย
x−2
13. ถ้ำ f(x) = จงหำ x→2 f(x)
lim
x + x−6 2
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
2x2 − x − 3
14. ถ้ำ f(x) = จงหำ x→−1 f(x)
lim
x+ 1
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
x + 9− 3
15. ถ้ำ f(x) = จงหำ x→0 f(x)
lim
x
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
x + 4− 2
16. ถ้ำ f(x) = จงหำ x→0 f(x)
lim
x
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….

9. เรื่องแคลคูลัสเบื้องต้น 9
โดยครูปอปลา คนส้วยสวย
x−9
17. lim
x→9 x − 3
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
3− x
18. lim
x→9 9 − x
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
2 − 4− k
19. lim
k→0 k
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
x+ 5 − 5
20. lim
x→0 x
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….
…………………………………………………………………………………….

10. เรื่องแคลคูลัสเบื้องต้น 10
โดยครูปอปลา คนส้วยสวย
แบบทดสอบที่ ١.٢
วิชา คณิตศาสตร์เพิ่มเติม (ค٤٣٢٠٢) ระดับชั้น มัธยมศึกษาปีที่ ٦ หน่วยการ
เรียนรู้ แคลคูลัสเบื้องต้น
เรื่อง ลิมตและความต่อเนื่องของฟังก์ชัน (٢) เวลา ١٥ นาที
ิ
คำาชี้แจง ข้อสอบฉบับนี้เป็นแบบปรนัยเลือกตอบจำำนวน 5 ข้อ เกี่ยวข้องกับ
เรื่องกำรพิจำรณำ หำลิมิตของฟังก์ชันจำกฟังก์ชัน ให้นักเรียนทำำ
ด้วยตนเองเพื่อทดสอบควำมเข้ำใจหลังจำก ทำำกิจกรรมตำมแบบฝึกทักษะที่
1.2 ครบแล้ว โดยกำรเลือกตอบลงในกระดำษคำำตอบ เพียงข้อละ 1 ตัว
เลือกเท่ำนั้น
จากฟั ง ก์ ช ั น ที ่ ก ำ า หนดให้ ท ั ้ ง ٦ ฟั ง ก์ ช ั น นี ้ ให้ พ ิ จ ารณาแล้ ว ตอบ
คำ า ถามข้ อ ٥ – ١
1 f (x) = 5x2 + 2x – 3
) 2) f(x) = 2 x + 1
x +1
x −4
2 x −1
3) f(x) = 4) f(x) =
x−2 x −1
x – 1 เมื่อ x > 2
x2 -4x + 5 เมื่อ < 2
4− x
5) f(x) = 6) f(x) = {
16 − x
٣ เมือ x = 2
่
1. ลิมิตของฟังก์ชันใด เมื่อ x เข้ำใกล้ 1 มีค่ำเท่ำกับ 0
ก. 1) ข. 2) ค. 3)
ง. 4)
2. ลิมิตของฟังก์ชันใด เมื่อ x เข้ำใกล้ 2 มีค่ำเท่ำกับ 4
ก. 3) ข. 4) ค. 5)
ง. 6)
3. ลิมิตของฟังก์ชันในข้อ 5 เมื่อ x เข้ำใกล้ 16 มีค่ำเท่ำไร
1 1
ก. 1 ข. 4
ค. 8
ง. หำค่ำไม่ได้
4. ลิมิตของฟังก์ชันในข้อ 6 เมื่อ x เข้ำใกล้ 2 มีค่ำเท่ำไร
ก. 0 ข. 1 ค. 2
ง. หำค่ำไม่ได้

11. เรื่องแคลคูลัสเบื้องต้น 11
โดยครูปอปลา คนส้วยสวย
5 ลิมิตของฟังก์ชันในข้อใด เมื่อ x เข้ำใกล้ 4 จะมีค่ำเท่ำกับ 6
ก. 3) ข. 5) ค. 6) ง. ไม่มีลิมิต
ของฟังก์ชันใดที่มีค่ำเป็น 6
เฉลยแบบฝึ ก ทั ก ษะที ่ ١.2
1. –8
2. 4 (٣) = 12
3. 3 (22) = 12
4. –3 (–2)5 = –3(–32) = 96
5. 5 + 2 = 7
6. 5 – 4 (7) = 5 – 28 = –23
7. (–1)2 + 9(–1) = 1 – 9 = –8
8. 3 (24) – 5 = 48 – 5 = 43
9. 2 (–1)3 – 5 (–1) + 8 = – 2 + 5 + 8 = 11
10. 04 + 3 (02) + 0 –6 = –6
11. 3
5 + 22 = 3 27 = 3
(x− 1) 1 1 1
lim = lim
12. x→1f(x) x→1 = lim = =
(x− 1)(x 1) x→1 (x+ 1) 1+ 1 2
+
(x− 2) 1 1 1
lim = lim
13. x→ 2f(x) x→ 2 = lim = =
(x+ 3)(x 2) x→ 2 x + 3 2+ 3 5
−
(x+ 1)(2x3)
−
=
14. xlimf(x) xlim = lim(2x 3)= 2( 1)− 3= − 5
− −
→ −1 → −1 x+ 1 x→ − 1
x + 9 − 3 x + 9 + 3 (x+ 9) 9−
lim =
15. x→0f(x) xlim ⋅ =
→0 x x + 9 + 3 x x + 9 + 3)
x+ 4 − 2 x+ 4 + 2 (x+ 4) 4
−
16. = lim ⋅ = lim
x→ 0 x x + 4 + 2 x→0 x x + 4 + 2
(x + 4) 4
− x 1
lim = lim = lim
x→ 0 x(x 4+ 2) x→ 0 x( x + 4 + 2) x→ 0 x + 4 + 2
+

12. เรื่องแคลคูลัสเบื้องต้น 12
โดยครูปอปลา คนส้วยสวย
1 1 1
= =
0+ 4 + 2 2+ 2 4
x− 9 x+ 3
17. =
limf(x) ⋅
x→ 9 x− 3 x+ 3
(x− 9)( x + 3)
= lim
x→ 9 (x− 9)
= lim x + 3)= 0 + 3= 3
(
x→ 9
= 9 + 3= 3+ 3= 6
3− x 3− x 3+ x
18. lim = lim ⋅
x→ 9 9− x x→ 9 9− x 3+ x
−
(9 x)
= lim
− +
x→ 9 (9 x)(3 x)
1
= lim
x→ 9 3+ x
1 1 1
= = =
3+ 9 3+ 3 6
2− 4 − k 2+ 4 − k 4− (4− k)
19. lim ⋅ = lim
x→ 0 k 2+ 4− k x→9 k(2 4− k)
+
k
= lim
+ 4− k)
x→ 0 k(2
1
= lim
x→ 0 2+ 4− k
1 1 1
= = =
2 + 4 − 0 2+ 2 4

13. เรื่องแคลคูลัสเบื้องต้น 13
โดยครูปอปลา คนส้วยสวย
x+ 5− 5 x+ 5+ 5 (x+ 5)− 5
20 lim ⋅ = lim
x→ 0 x x + 5 + 5 x→ 0 x( x + 5 + 5)
x
= lim
x→ 0 x( x + 5 + 5)
1
= lim
x→ 0 x + 5 + 5
1 1
= =
0+ 5 + 5 2 5