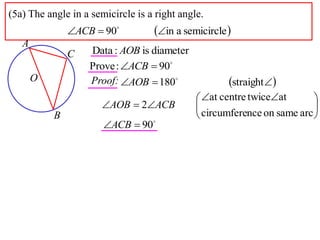
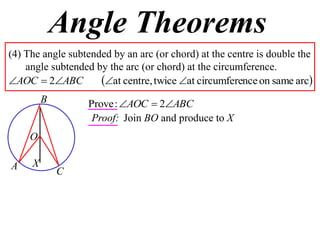
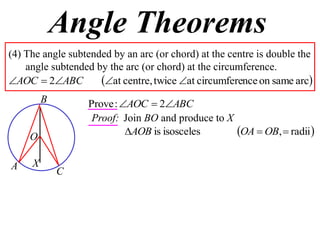
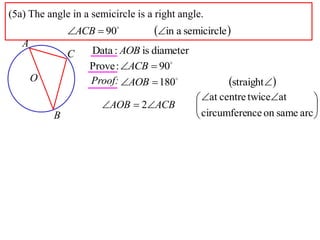
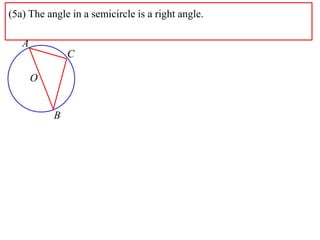
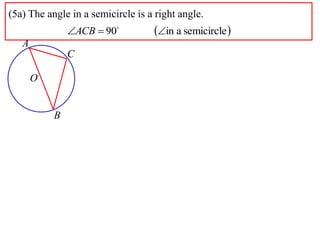
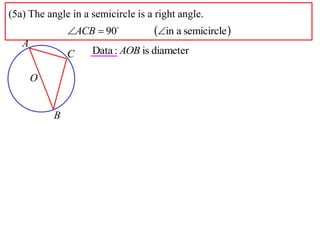
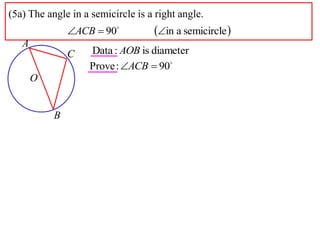
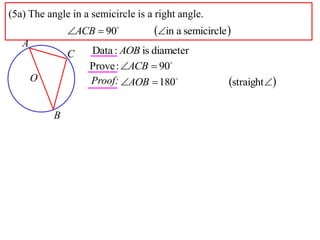
The document discusses several angle theorems: 1) The angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at the circumference. This is proven using properties of isosceles triangles. 2) The angle in a semicircle is a right angle of 90 degrees. This is proven using the fact that the angle at the center of a full circle is 180 degrees, and the relationship that the central angle is double the circumference angle. 3) Several exercises involving applying these angle theorems are listed at the end.

1. Angle Theorems

2. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.

3. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
B
O
A C

4. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B
O
A C

5. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
O
A C

6. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O
A X
C

7. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
A X
C

8. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
 OBA  OAB base' s isosceles 
A X
C

9. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
 OBA  OAB base' s isosceles 
A X AOX  OBA  OAB exterior OAB 
C

10. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
 OBA  OAB base' s isosceles 
A X AOX  OBA  OAB exterior OAB 
C
 AOX  2OBA

11. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
 OBA  OAB base' s isosceles 
A X AOX  OBA  OAB exterior OAB 
C
 AOX  2OBA
 COX  2OBC by similar method

12. Angle Theorems
(4) The angle subtended by an arc (or chord) at the centre is double the
angle subtended by the arc (or chord) at the circumference.
AOC  2ABC at centre, twice at circumference on same arc
B Prove : AOC  2ABC
Proof: Join BO and produce to X
O AOB is isosceles OA  OB,  radii 
 OBA  OAB base' s isosceles 
A X AOX  OBA  OAB exterior OAB 
C
 AOX  2OBA
 COX  2OBC by similar method
 AOC  2ABC

13. (5a) The angle in a semicircle is a right angle.

14. (5a) The angle in a semicircle is a right angle.
A
C
O
B

15. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C
O
B

16. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
O
B

17. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
Prove : ACB  90
O
B

18. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
Prove : ACB  90
O Proof: AOB  180 straight 
B

19. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
Prove : ACB  90
O Proof: AOB  180 straight 
 at centre twiceat 
AOB  2ACB  
B  circumference on same arc 

20. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
Prove : ACB  90
O Proof: AOB  180 straight 
 at centre twiceat 
AOB  2ACB  
B  circumference on same arc 
ACB  90

21. (5a) The angle in a semicircle is a right angle.
ACB  90 in a semicircle 
A
C Data : AOB is diameter
Prove : ACB  90
O Proof: AOB  180 straight 
 at centre twiceat 
AOB  2ACB  
B  circumference on same arc 
ACB  90
Exercise 9B; 1 ace etc, 2, 6, 8ac, 9ab, 10ac, 11ac, 12, 13