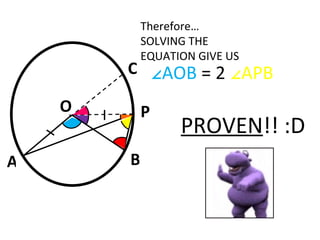
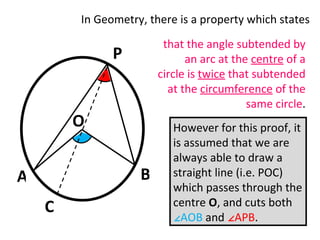
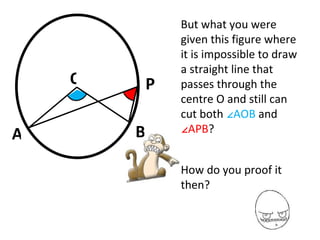
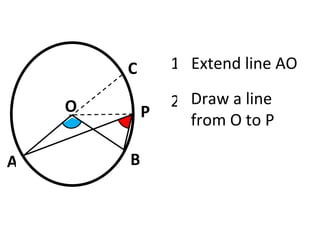
This document summarizes how to prove that the angle subtended by an arc at the centre of a circle is twice that subtended at the circumference, even when a line cannot be drawn through the centre cutting both angles. It does this by extending one arc line to the centre, then using properties of isosceles triangles and angles on a straight line to derive an equation that solves to the desired property.

1. (a) Proving Angle Properties of Circles

2. A B P O C that the angle subtended by an arc at the centre of a circle is twice that subtended at the circumference of the same circle .  ∠ AOB = 2 x ∠APB e.g. If ∠AOB = 50°, then according to the property, ∠APB = 25°. In Geometry, there is a property which states However for this proof, it is assumed that we are always able to draw a straight line (i.e. POC) which passes through the centre O , and cuts both ∠AOB and ∠APB .

3. A B P O But what you were given this figure where it is impossible to draw a straight line that passes through the centre O and still can cut both ∠AOB and ∠APB ? How do you proof it then?

4. Let us show you how to :D

5. A B P O 1 Extend line AO 2 Draw a line from O to P C

6. A B P O ∠ AOB + ∠BOP + ∠POC = 180° (adj. angles on a straight line) C ∠ BOP = 180 ° – 2 x ∠OPB ∠ OBP = ∠OPB (isosceles triangle) P O

7. A B P O C ∠ AOB + 180 ° – 2 x ∠OPB + ∠POC = 180 ° ∠ OPB = ∠OPA + ∠APB B P O A ∠ AOB – 2( ∠OPA + ∠APB ) + ∠POC = O ∠ AOB – 2 ∠OPA – 2 ∠APB + ∠POC = O

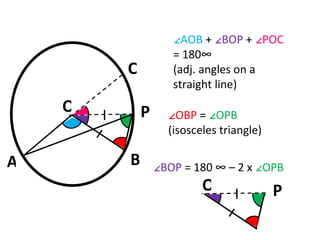
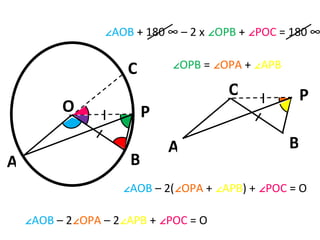
8. A B P O C ∠ POC = 2 ∠OPA [ ∠OPA = ∠OAP (isosceles triangle), ∠ POC = ∠OAP + ∠OPA (external angles)] B P O C A ∠ AOB - 2 ∠OPA - 2 ∠APB + ∠POC = O

9. A B P O C Therefore… SOLVING THE EQUATION GIVE US ∠ AOB = 2 ∠APB PROVEN !! :D

10. The end :D

11. Done by Ming Xuan Cheng Mun Natalie Jerald Xin Yao Xin Yi