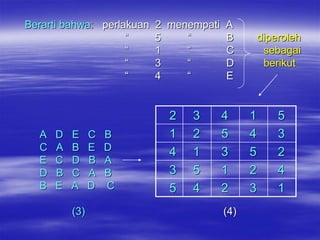
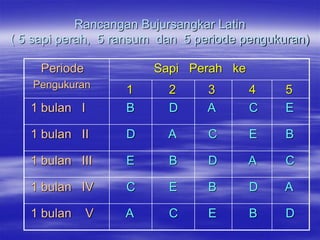
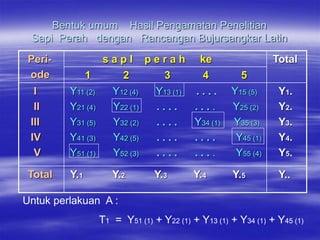
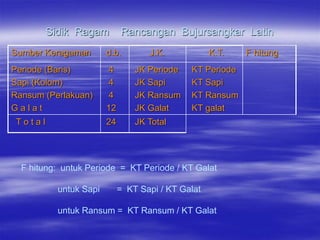
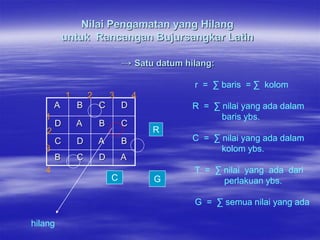
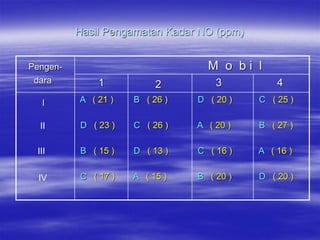
Rancangan Bujursangkar Latin merupakan rancangan percobaan yang memiliki dua ulangan yaitu baris dan kolom. Banyaknya perlakuan sama dengan banyaknya baris dan kolom. Setiap perlakuan hanya menempati satu sel dalam tabel. Data dianalisis menggunakan sidik ragam untuk mengetahui pengaruh baris, kolom, dan perlakuan terhadap hasil pengamatan.

1. RANCANGAN
BUJURSANGKAR LATIN
( LATIN SQUARE DESIGN)
Ir. Zakaria Ibrahim, MM

2. CIRI-CIRI R.B.L.
(1) Pada unit percobaan dilakukan batasan pengelompokan ganda →
seperti dua RAK, dua kelompok berbeda dengan baris dan kolom sebagai ulangan.
(2) Banyaknya perlakuan sama dengan banyaknya ulangan
(3) Banyaknya satuan percobaan = kuadrat (square) perlakuan atau ulangannya
(4) Setiap perlakuan diberi lambang huruf latin besar → Misalnya: A, B, C, D
sehingga disebut Latin Square Design
(5). Terdapat 3 sumber keragaman:
- baris (row) → misalnya : waktu pengamatan
- lajur (kolom) → misalnya : bahan percobaan
- perlakuan → misalnya : ransum
(disamping pengaruh acak)
Ke 3 keragaman tsb. jumlahnya sama besar = r

3. Model Matematika RBL:
Model: Yi j k = μ + βi + +
j k + εi j k
baris → i = 1, 2, . . . 5
lajur (kolom)→ j = 1, 2, . . . 5
perlakuan → k = 1, 2, . . . 5
Yi j k = hasil pengamatan pada baris ke-i, lajur (kolom)
ke-j, untuk perlakuan ke-k
μ = nilai tengah umum
β i = pengaruh baris (row) ke i
j = pengaruh lajur (kolom) ke j
k = pengaruh perlakuan ke k
εi j k = pengaruh acak (galat percobaan) pada baris kei,
lajur ke-j , yang diberikan utk perlakuan ke k .

4. Ulangan pada RBL
RBL sebenarnya mempunyai dua ulangan:
Ulangan I (baris)
Ulangan II (kolom atau lajur)
Sedang banyaknya perlakuan =
banyaknya ulangan I =
banyaknya ulangan II
↓
Sehingga :
Banyaknya baris (ulangan I) =
Banyaknya kolom (ulangan II) =
Banyaknya perlakuan = r

5. Penempatan perlakuan pada RBL:
Cara pengacakannya dengan acak terbatas →
↓
Tiap perlakuan hanya boleh terdapat sekali dalam tiap baris dan
tiap kolom
Misalnya Rancangan Bujursangkar Latin, dengan
perlakuan 1, 2,3,4 dan 5.
↓
(1). Buat latin baku secara acak → A, B, C, D dan E
( baris dan lajur pertama, hurufnya menurut
urutan abjad)
A B C D E
B C D E A
C D E A B
D E A B C
E A B C D
(2). Acak menurut baris
(3). Acak menurut kolom

6. A B C D E B C D E A A D E C B
B C D E A D E A B C C A B E D
C D E A B A B C D E E C D B A
D E A B C E A B C D D B C A E
E A B C D C D E A B B E A D C
(1) (2) (3)
(4). Penempatan perlakuan ke dalam bujur sangkar (3),
dengan bantuan bilangan acak misalnya didapat su-
sunan: 2 5 1 3 4
↓

7. Berarti bahwa: perlakuan 2 menempati A
― 5 ― B diperoleh
― 1 ― C sebagai
― 3 ― D berikut
― 4 ― E
2 3 4 1 5
A D E C B 1 2 5 4 3
C A B E D 4 1 3 5 2
E C D B A
D B C A B 3 5 1 2 4
B E A D C 5 4 2 3 1
(3) (4)

8. Pengolahan data dan sidik ragam RBL:
Sebagai contoh
Penelitian terhadap sapi perah 5 ekor dgn jenis sama
(ttp mungkin keadaan fisik tak sama, dan juga umur tak
sama) → oleh karena itu ke 5 ekor sapi tsb dpt dijadikan
kelompok.
Sapi-sapi tsb diberi 5 macam ransum yang berbeda
ialah ransum A, B, C, D dan E.
Pengamatan dilakukan thdp produksi air susunya se-
lama 1 bulan (disebut periode I ), setelah itu sapi-sapi
tsb diistirahatkan pada waktu ttt sampai pengaruh pem-
berian ransum tidak ada lagi.

9. Kemudian diberi perlakuan kembali dgn 5 macam ran-
sum tsb, akan ttp pemberiannya (macam ransum) berbeda
dengan semula untuk sapi yang sama → dalam hal ini sapi
tetap, tetapi ransumnya berbeda.
Dilakukan kembali pengamatan thdp produksi air susu-
nya selama 1 bulan → disebut periode II. Selanjutnya diis-
tirahatkan kembali seperti di atas, dan seterusnya sehingga
lengkaplah semua perlakuan untuk tiap sapi (sampai perio-
de v )
Jadi terdapat 5 sapi perah jenis sama ( 1, 2, 3, 4 dan 5 )
5 perlakuan ransum (A, B, C, D dan E )
5 periode pengukuran (I, II, III,IV dan V )

10. Rancangan Bujursangkar Latin
( 5 sapi perah, 5 ransum dan 5 periode pengukuran)
Periode Sapi Perah ke
Pengukuran
1 2 3 4 5
1 bulan I B D A C E
1 bulan II D A C E B
1 bulan III E B D A C
1 bulan IV C E B D A
1 bulan V A C E B D

11. Model: Yi j k = μ + βi + j + k + εi j k
periode → i = 1, 2, . . . . . 5
sapi →
j = 1, 2, . . . . . 5
ransum → k = 1, 2, . . . . .5
Yi j k = produksi susu selama 1 bulan dari sapi ke - j yg
menerima perlakuan ke - k pada periode ke - i
β i = pengaruh periode (baris) ke i
j = pengaruh sapi (kolom) ke j
k = pengaruh ransum (perlakuan) ke k
εi j k = pengaruh acak (galat percobaan) pada periode
ke i , sapi ke j , yang diberikan utk perlakuan ran-
sum ke k .

12. Bentuk umum Hasil Pengamatan Penelitian
Sapi Perah dengan Rancangan Bujursangkar Latin
Peri- sapI perah ke Total
ode 1 2 3 4 5
I Y11 (2) Y12 (4) Y13 (1) .... Y15 (5) Y1.
II Y21 (4) Y22 (1) .... .... Y25 (2) Y2.
III Y31 (5) Y32 (2) .... Y34 (1) Y35 (3) Y3.
IV Y41 (3) Y42 (5) .... .... Y45 (1) Y4.
V Y51 (1) Y52 (3) .... .... Y55 (4) Y5.
Total Y.1 Y.2 Y.3 Y.4 Y.5 Y..
Untuk perlakuan A :
T1 = Y51 (1) + Y22 (1) + Y13 (1) + Y34 (1) + Y45 (1)

13. Jumlah kuadrat:
2
2 2 2 Y..
JK Total = Y11(2) + Y21(4) + ........+ Y55(4) —
25
2 2 2 2
JK Periode = Y1. + Y2. + . . . . . . . . + Y5. Y..
(JK Baris) 5 25
2 2 2 2
JK Sapi = Y.1 + Y.2 + . . . . . . . . + Y.5 Y..
(JK Kolom) 5 25
2 2 2 2
JK Ransum = T1 + T2 + . . . . . + T5 Y..
(JK Perlakuan) 5 25
JK Galat = JK Total – JK Periode – JK Sapi – JK Ransum

14. Sidik Ragam Rancangan Bujursangkar Latin
Sumber Keragaman d.b. J.K. K.T. F hitung
Periode (Baris) 4 JK Periode KT Periode
Sapi (Kolom) 4 JK Sapi KT Sapi
Ransum (Perlakuan) 4 JK Ransum KT Ransum
Galat 12 JK Galat KT galat
Total 24 JK Total
F hitung: untuk Periode = KT Periode / KT Galat
untuk Sapi = KT Sapi / KT Galat
untuk Ransum = KT Ransum / KT Galat

15. Nilai Pengamatan yang Hilang
untuk Rancangan Bujursangkar Latin
→ Satu datum hilang:
r = ∑ baris = ∑ kolom
1 2 3 4
A B C D R = ∑ nilai yang ada dalam
1 baris ybs.
D A B C
2 R
C D A B C = ∑ nilai yang ada dalam
3 kolom ybs.
B C D A
4 T = ∑ nilai yang ada dari
C G perlakuan ybs.
G = ∑ semua nilai yang ada
hilang

16. 
 r (R+C+T)–2G
 Y = ( r – 1) ( r – 2 )
 # Merupakan penduga → tidak memberikan sokongan thdp galat
 percobaan (d.b. galat berkurang satu)
 # J.K. Perlakuan berbias positif → K.T. Perlakuan agak tinggi
 {G–R–C–(r–1)T}2
Bias =
 {( r – 1) ( r – 2 )} 2






17. S.K. d.b.
Baris (r–1)
Kolom (r–1)
Perlakuan (r–1)
Galat (r–1)(r–2)–1
Total ( r2 – 2 )
Bias tsb dihitung → J.K. Perlakuan tak berbias dpt diketemukan
→ K.T. Perlakuan terkoreksi dpt dicari
→ F hitung terkoreksi diketemukan
Bila bbrp data hilang, dicari dgn menerapkan berkali-kali rumus
satu datum hilang, seperti halnya pada Ranc Acak Kelomp.

18. Efisiensi Relatif Rancangan Bujursangkar Latin
terhadap Rancangan Acak Kelompok
1 2 3 4
1
A B C D
2
D A B C
C D A B
3
B C D A
4
Sidik Ragam RBL:
S.K. d.b. J.K. K.T
.
Baris ( r – 1 ) = fb JKB KTB
Kolom ( r – 1 ) = fk JKK KTK
Perlakuan ( r – 1 ) = fp JKP KTP
Galat ( r – 1 ) ( r – 2 ) = fg = f1 JKG KTG
Total ( r2 – 1 ) JKT -

19. Seandainya percobaan dilaksanakan dgn RAK,
dengan baris sebagai kelompok
( kolom diabaikan)
S.K. d.b. J.K. K.T
Kelompok (baris) (r – 1) = fb JKK KTK
Perlakuan (r – 1) = fp JKP KTP
Galat (r – 1)2 = f2 JKG' KTG'
Total ( r2 – 1) JKT
fk x KTK + ( fp + fg ) x KTG
KTG' ( RAK ) = ( fk + f p + f g )

20. ( f1 + 1 ) ( f2 + 3 ) ( 1 / KTG )
E RBL terhadap RAK = X 100%
(baris sbg kelomp.) ( f2 + 1 ) ( f1 + 3 ) ( 1 / KTG' (RAK)
( f1 + 1 ) ( f 2 + 3 ) KTG ' (RAK)
= X X 100%
( f2 + 1 ) ( f 1 + 3 ) KTG
Dimana: f1 = fg = ( r – 1 ) ( r – 2 )
f2 = ( r – 1 )2

21. Jika percobaan Rancangan Bujursangkar Latin
dipandang sebagai Rancangan Acak Kelompok,
dengan kolom sebagai kelompok
( baris diabaikan)
fb X KTB + ( fp + fg ) x KTG
KTG‘' ( RAK ) = ( fb + fp + fg )
( f1 + 1 ) ( f 2 + 3 ) KTG'' ( RAK)
E RBL terhadap RAK =
(kolom sbg. Kelomp.) ( f2 + 1) ( f1 + 3 ) X KTG X 100%
Kesimpulan → sama dgn Efisiensi RAK

22. T U T O R I A L
M O D U L VIII

23. TUTORIAL
TUGAS BAB 9 No II
(Dikerjakan di lembaran Kertas)
TUGAS PEKERJAAN RUMAH
(Dikerjakan pada Buku Ajar)
- BAB 9 No I
- BAB 9 No II
(Soal serupa tetapi tidak sama
untuk setiap mahasiswa)

24. Hasil Pengamatan Kadar NO (ppm)
Pengen- M o bi l
dara 1 3 4
2
I A ( 21 ) B ( 26 ) D ( 20 ) C ( 25 )
II D ( 23 ) C ( 26 ) A ( 20 ) B ( 27 )
III B ( 15 ) D ( 13 ) C ( 16 ) A ( 16 )
IV C ( 17 ) A ( 15 ) B ( 20 ) D ( 20 )