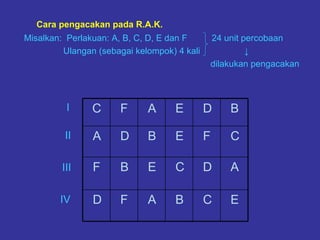
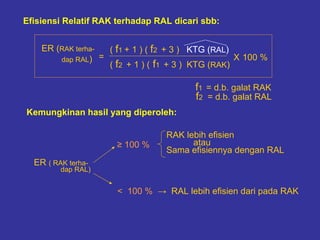
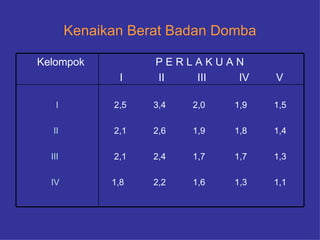
Dokumen ini membahas tentang rancangan acak kelompok (RAK) dan penggunaannya dalam percobaan yang melibatkan berbagai sumber keragaman. Diberikan contoh penerapan RAK dalam eksperimen padi dan ternak babi, serta teknik pengacakan dan analisis data termasuk sidik ragam. Kesimpulan menyoroti efisiensi penggunaan RAK dibandingkan rancangan acak lengkap (RAL) dalam meraih hasil percobaan.

1. RANCANGAN ACAK KELOMPOK
(RANDOMIZED BLOCK DESIGN)
atau
RANCANGAN KELOMPOK LENGKAP TERACAK
(RANDOMIZED COMPLITE BLOCK DESIGN)
Prof.Dr. Kusriningrum

2. Eka Arah (One way classification)
→ 1 sumber keragaman, yaitu
perlakuan
KLASIFIKASI (disamping pengaruh galat / acak)
Banyak Arah (Multi way classification)
→ lebih dari 1 sumber keragaman
(disamping pengaruh galat / acak)
Eka Arah → - Rancangan Acak Lengkap
Banyak Arah → - Rancangan Acak Kelompok
- Rancangan Bujursangkar Latin

3. RANCANGAN ACAK KELOMPOK
Dipergunakan bila:
( I ). Media atau bahan percobaaqn tidak seragam
(tidak dapat dianggap seragam) → perlu
dikelompokkan
( II ). Terdapat 2 sumber keragaman :
a. media / tempat, bahan / materi percobaan
berbeda
b. perlakuan yang diberikan
- (selain pengaruh acak)

4. CONTOH: Klasifikasi Banyak Arah →
( I ). Percobaan padi, petak-petak percobaan pada ketinggian tak
sama: - Perlakuan: 6 macam → keadaannya tidak sama
- ulangan : 5 → diperlukan 5 petak (pada ketinggian
yang tidak sama)
Terdapat 2 perbedaan, yaitu perlakuan & keadaan petak
( II ). Percobaan dengan ternak babi:
- perlakuan: 4 macamdiperlukan 24 ekor anak babi
- ulangan: 6 kali → (yang tersedia 6 induk masing-
masing dengan 4 anak)
Terdapat 2 perbedaan, yaitu perlakuan & induk babi
( I ) & ( II ) 2 macam yang berbeda, dipergunakan
Rancangan Acak Kelompok

5. Model umum matematika untuk R.A.K.:
Pengaruh
Kelompok ke j
Nilai
tengah umum
Yij = μ + ‫ז‬i + βj + εij i = 1, 2, . . . . , t
J = 1, 2, . . . . , n
Nilai pengamatan pada
Perlakuan ke i kelompok ke j
Pengaruh
Perlakuan ke i
Pengaruh acak pada
perlakuan ke i kelompok ke j

6. ULANGAN PADA RAK:
- Ulangan pada RAK sebenarnya juga merupakan
kelompok dari RAK
- Besar ulangan minimal untuk RAK:
derajat bebas Galat ≥ 15.
( t -1) (n -1) ≥ 15 → t = banyaknya perlakuan
n = banyaknya ulangan
Misalnya banyaknya perlakuan = 4, maka ulangan minimal yang
diperlukan: (4 -1) (n -1) ≥ 15
3n – 3 ≥ 15
3n ≥ 18
n ≥ 18/3
n≥6

7. Cara pengacakan pada R.A.K.
Misalkan: Perlakuan: A, B, C, D, E dan F 24 unit percobaan
Ulangan (sebagai kelompok) 4 kali ↓
dilakukan pengacakan
I C F A E D B
II A D B E F C
III F B E C D A
IV D F A B C E

8. PENGOLAHAN DATA dan SIDIK RAGAM
CONTOH:
Percobaan dengan ternak babi, yang mendapat perlakuan
4 macam ransum pakan (perlakuan P, Q, R dan S) dan
ulangan 6 kali, hasil pengamatan pertambahan bobot
badan sbb:
(Ulangan 6 kali, karena diperoleh anak2 babi dari induk2 yang
berbeda → 6 induk babi, masing2 dengan 4 anak )
Perla- Induk (Kelompok / Blok) Total
kuan 1 2 3 4 5 6
P Y11 Y12 . . . Y16 Y1.
Q Y21 Y22 Y26 Y2.
R Y31 Y32 Y36 Y3.
S Y41 Y42 Y46 Y4.
Total Y.1 Y.2 . . . Y.6 Y. .

9. n
t
Hasil pengamatan pertambahan berat badan yang
Y1 2 = menerima perlakuan ransum ke1 dan kelompok /
i=1 induk ke 2
j=1
Model umum matematikanya:
Pertambahan bobot badan
pada perlakuan ransum ke i pengaruh kelompok /
dan kelompok / induk ke j induk ke j
Yi j = μ + ‫ז‬i + βj + ε ij i = 1, 2, 3, 4
j = 1, 2, . . . . , 6
nilai tengah umum
pengaruh perlakuan pengaruh acak pada perlakuan
pemberian ransum ke i ransum ke i dan kelompok/induk ke j

10. Jumlah Kuadrat:
t 4 2
y. . 2 = ∑ y i . y. . 2
J.K.P = ∑ y i. 2
i=1 n tn i=1 6 24
n 2 2 6 2 2
y. j y. . y. j y. .
J.K.K. = ∑ = ∑
j=1 t tn j=1 4 24
t n 2 y. . 2
J.K.T = ∑ ∑ yij
tn
i=1 j=1
J.K.G. = J.K.T. J.K.P. J.K.K.

11. SIDIK RAGAM
S.K. d.b. J.K. K.T. F hitung F tabel
0,05 0,01
Kelompok 5 J.K.K. K.T.K KTK / KTG
Perlakuan 3 J.K.P. K.T.P KTP / KTG
Galat 15 J.K.G. K.T.G
Total 23 J.K.T.
Sebagai penguji hipotesis: H0 → 0 = 4‫= ז2 = ז3 = ז‬ 1 ‫ז‬
H1 → paling sedikt salah satu ‫ז‬i ≠ 0
Bila perbedaan antar induk tidak diperhatikan, maka percobaan
menggunakan Rancangan Acak Lengkap (R.A.L)
Kapan memakai Rancangan Acak Kelompok (R.A.K) ter-
gantung keadaan yang dihadapi (tak selalu harus R.A.K,
kadang-kadang cukup dengan R.A.L saja)

12. CONTOH SOAL: Percobaan dengan 6 perlakuan dan 4 ulangan, me-
makai RAK.
Perlakuan Kelompok Total
I II IV V
1 4,4 5,9 . 4,1 20,4
2 3,3 1,9 . 7,1 17,2
3 . . . . .
4 . . . . .
5 . . . . .
6 6,6 7,3 . 6,7 28,1
Total 31,6 30,6 . 132,7
34,5
2 2 2 2
JKT = 4,4 + 3,3 + . . . . . .+ 6,7 132,7 = 54,51
2 24
2 2
31,6 + 30,6 + . . . . . .+ 34,5
JKK = F.K. = 3,14
6

13. 2 2 2
20,4 + 17,2 + . . . . . . .+ 28,1
JKP = F.K. = 31,65
4
JKG = 54,51 3,14 31,65 = 19,72
SIDIK RAGAM:
S.K. d.b. J.K. K.T. F hitung F tabel
0,05 0,01
Kelompok 3 3,14 1,05 0,80 3,29 5,42
Perlakuan 5 31,65 6,33 4,83** 2,90 4,56
Galat 15 19,72 1,31
Total 23 54,51
Kesimpulan: perlakuan memberikan pengaruh sangat nyata
( p < 0,01) terhadap hasil pengamatan

14. Efisiensi relatif RAK terhadap RAL:
Bila percobaan dilaksanakan dengan RAK, tetapi perhitungannya
dipakai RAL →
Mana yang lebih efisien menggunakan RAK ataukah RAL ?
Maka: - untuk J.K. dari RAL tidak dapat diperoleh / dihitung
- untuk K.TG dari RAL dapat dikira-kira dari K.TG nya RAK
SIDIK RAGAM untuk RAL:
S.K. d.b. J.K. KT
Perlakuan 5
Galat 18 KTG (RAL)
Total 23

15. Perkiraan KTG dari RAL dihitung sbb:
fk x KTK + ( fp + fg ) x KTG
KTG (RAL) = ( f k + fp + fg )
KTG (RAL) = nilai perkiraan KTG dari RAL
KTK = Kuadrat Tengah Kelompok
KTG = Kuadrat Tengah Galat dari RAK
fk = d.b. kelompok
fp = d.b. perlakuan dari RAK
fg = d.b. galat

16. Efisiensi Relatif RAK terhadap RAL dicari sbb:
ER (RAK terha- ( f1 + 1 ) ( f2 + 3 ) KTG (RAL)
dap RAL) = X 100 %
( f2 + 1 ) ( f1 + 3 ) KTG (RAK)
f1 = d.b. galat RAK
f2 = d.b. galat RAL
Kemungkinan hasil yang diperoleh:
RAK lebih efisien
≥ 100 % atau
Sama efisiennya dengan RAL
ER ( RAK terha-
dap RAL)
< 100 % → RAL lebih efisien dari pada RAK

17. CONTOH (lihat contoh soal dan penyelesaiannya di atas)
Dari contoh soal tersebut diperoleh:
KTK dari RAK = 1,05 fk = 3 fg = 15
KTG dari RAK = 1,31 fp = 5
fk x KTK + ( fp + fg ) x KTG
KTG (RAL) = ( fk + fp + f g )
3 x 1,05 + ( 5 + 15 ) x 1,31
= = 1,1196
( 3 + 5 + 15)
ER RAK terha- = ( f1 + 1 ) ( f2 + 3 ) KTG (RAL) X 100% diketahui:
dap RAL ( f2 + 1 ) ( f1 + 3 ) KTG (RAK) f1 =
15
f2 =
18 = X 100% = 96%
(15 + 1 ) (18 + 3) 1,1196
(18 + 1 ) (15 + 3) 1,31

18. ER RAK terhadap RAL = 96% < 100%
↓
Kesimpulan: penggunaan RAL lebih efisien dari pada RAK
( Karena 96 kali ulangan RAL memberikan infor-
masi sama banyaknya dengan bila dilakukan
100 kali ulangan dalam RAK )
-----

19. TUTORIAL
TUGAS BAB 7 No II
(Dikerjakan di lembaran Kertas)
TUGAS PEKERJAAN RUMAH
(Dikerjakan pada Buku Ajar)
- BAB 7 No I
- BAB 7 No II
(Soal serupa tetapi tidak sama
untuk setiap mahasiswa)

20. Kenaikan Berat Badan Domba
Kelompok PERLAKUAN
I II III IV V
I 2,5 3,4 2,0 1,9 1,5
II 2,1 2,6 1,9 1,8 1,4
III 2,1 2,4 1,7 1,7 1,3
IV 1,8 2,2 1,6 1,3 1,1